Kommutativ ring

Inom matematiken är en kommutativ ring en ring där multiplikationsoperationen är kommutativ . Studiet av kommutativa ringar kallas kommutativ algebra . Komplementärt icke-kommutativ algebra studiet av ringegenskaper som inte är specifika för kommutativa ringar. Denna distinktion är ett resultat av det stora antalet grundläggande egenskaper hos kommutativa ringar som inte sträcker sig till icke-kommutativa ringar.

Definition och första exempel

Definition

Ytterligare information om definitionen av ringar: Ring (matematik)

En ring är en uppsättning $R$ utrustad med två binära operationer , dvs operationer som kombinerar två valfria element i ringen till en tredje. De kallas addition och multiplikation och betecknas vanligtvis med " $+$ " och " $\cdot$ "; t.ex. $a+b$ och $a\cdot b$ . För att bilda en ring måste dessa två operationer uppfylla ett antal egenskaper: ringen måste vara en abelsk grupp under addition såväl som en monoid under multiplikation, där multiplikation fördelar sig över addition; dvs $a\cdot \left(b+c\right)=\left(a\cdot b\right)+\left (a\cdot c\right)$ . Identitetselementen för addition och multiplikation betecknas $0$ respektive $1$ .

Om multiplikationen är kommutativ, dvs

$$a\cdot b=b\cdot a,$$

kallas ringen $R$ kommutativ . I resten av denna artikel kommer alla ringar att vara kommutativa, om inte annat uttryckligen anges.

Första exemplen

Ett viktigt exempel, och i någon mening avgörande, är ringen av heltal $\mathbb {Z}$ med de två operationerna addition och multiplikation. Eftersom multiplikationen av heltal är en kommutativ operation, är detta en kommutativ ring. Det brukar betecknas $\mathbb {Z}$ som en förkortning av det tyska ordet Zahlen (siffror).

Ett fält är en kommutativ ring där $0\not =1$ och varje element som inte är noll $a$ är inverterbart; dvs har en multiplikativ invers $b$ så att $a\cdot b=1$ . Därför är varje fält per definition en kommutativ ring. De rationella , reella och komplexa talen bildar fält.

Om $R$ är en given kommutativ ring, så bildar mängden av alla polynom i variabeln $X$ vars koefficienter är i $R$ polynomringen , betecknad R $\ displaystil R\vänster[X\höger]}$ . Detsamma gäller för flera variabler.

Om $V$ är något topologiskt utrymme , till exempel en delmängd av några ${\displaystyle \mathbb {R} ^{n}} ,$ real- eller komplexvärdade kontinuerliga funktioner på formen $V$ en kommutativ ring. Detsamma gäller för differentierbara eller holomorfa funktioner , när de två begreppen är definierade, såsom för $V$ en komplex mångfald .

Delbarhet

I motsats till fält, där varje element som inte är noll är multiplikativt inverterbart, är begreppet delbarhet för ringar rikare. Ett element $a$ av ring $R$ kallas en enhet om det har en multiplikativ invers. En annan speciell typ av element är nolldivisorerna , dvs ett element $a$ så att det finns ett icke-noll element $b$ i ringen så att $ab=0$ . Om $R$ inte har några nolldelare som inte är noll, kallas det en integral domän (eller domän). Ett element $a$ som uppfyller $a^{n}=0$ för något positivt heltal $n$ kallas nilpotent .

Lokaliseringar

Huvudartikel: Lokalisering av en ring

Lokaliseringen av en ring är en process där vissa element görs inverterbara, dvs multiplikativa inverser läggs till ringen. Konkret, om $S$ är en multiplikativt sluten delmängd av $R$ (dvs. när $s,t\in S$ så är $st$ ) då består lokaliseringen av $R$ vid $S$ , eller ring av bråk med nämnare i $S$ , vanligtvis betecknad $S^{-1}R$ av symboler

${\frac {r}{s}}$ med $r\in R,s\in S$

omfattas av vissa regler som efterliknar annulleringen som är bekant från rationella tal. I detta språk $\mathbb {Q}$ lokaliseringen av $\mathbb {Z}$ vid alla heltal som inte är noll. Denna konstruktion fungerar för vilken integral domän $R$ som helst istället för $\mathbb {Z}$ . Lokaliseringen $\left(R\backslash \left\{0\right\}\right)^{-1}R$ är ett fält som kallas kvotfältet för ${ \displaystyle R}$ .

Ideal och moduler

I det följande betecknar R en kommutativ ring.

Många av följande begrepp finns också för inte nödvändigtvis kommutativa ringar, men definitionerna och egenskaperna är vanligtvis mer komplicerade. Till exempel är alla ideal i en kommutativ ring automatiskt dubbelsidiga , vilket förenklar situationen avsevärt.

Moduler

Huvudartikel: Modul

För en ring ${\displaystyle R} är$ en $R$ - modul $M$ som vad ett vektorrum är för ett fält. Det vill säga element i en modul kan läggas till; de kan multipliceras med element av $R$ med samma axiom som för ett vektorrum.

Studiet av moduler är betydligt mer involverat än det av vektorrum , eftersom det finns moduler som inte har någon grund , det vill säga inte innehåller en spännmängd vars element är linjärt oberoende . En modul som har en bas kallas en fri modul , och en undermodul till en fri modul behöver inte vara ledig.

En modul av ändlig typ är en modul som har en ändlig spännvidd. Moduler av finit typ spelar en grundläggande roll i teorin om kommutativa ringar, liknande rollen för de finita dimensionella vektorutrymmena i linjär algebra . I synnerhet Noeteriska ringar (se även § Noeteriska ringar nedan) definieras som ringarna så att varje submodul av en modul av finit typ också är av finit typ.

Ideal

Huvudartiklar: Ideal- och faktorring

Idealen för en ring $R$ är undermodulerna till $R$ , dvs modulerna som ingår i $R$ . Mer detaljerat är en ideal $I$ en icke-tom delmängd av $R$ så att för alla $r$ i $R$ , $i$ och $j$ i $I$ , både $ri$ och $i+j$ finns i $I$ . För olika tillämpningar är förståelsen av en ring ideal av särskild vikt, men ofta går man vidare med att studera moduler i allmänhet.

Varje ring har två ideal, nämligen nollidealet { $\displaystyle \left\{0\right\}}$ och $R$ , hela ringen. Dessa två ideal är de enda just om $R$ är ett fält. Givet någon delmängd $F=\left\{f_{j}\right\}_{j\in J}$ av $R$ (där $J$ är någon indexuppsättning), idealet som genereras av $F$ är det minsta idealet som innehåller $F$ . På motsvarande sätt ges den av finita linjära kombinationer

$$r_{1}f_{1}+r_{2}f_{2}+\dots +r_{n}f_{n}.$$

Huvudsakliga idealdomäner

Om $F$ består av ett enda element $r$ , består idealet som genereras av $F$ av multiplerna av $r$ , dvs. elementen i formen $rs$ för godtyckliga element $s$ . Ett sådant ideal kallas ett huvudideal . Om varje ideal är ett principideal, kallas ${\displaystyle R} en$ principiell idealring ; två viktiga fall är $\mathbb {Z}$ och ${\displaystyle k\left[X\right]} ,$ polynomringen över ett fält $k$ . Dessa två är dessutom domäner, så de kallas principiella idealdomäner .

Till skillnad från för allmänna ringar, för en principiell idealdomän, är egenskaperna hos enskilda element starkt knutna till egenskaperna hos ringen som helhet. Till exempel är vilken principiell idealdomän ${\displaystyle R} som helst$ en unik faktoriseringsdomän (UFD) vilket betyder att vilket element som helst är en produkt av irreducerbara element, på ett (upp till omordning av faktorer) unikt sätt. Här kallas ett element a i en domän irreducible om det enda sättet att uttrycka det som en produkt

$$a=bc,$$

är antingen $b$ eller $c$ vara en enhet. Ett exempel, viktigt i fältteorin , är irreducerbara polynom , dvs irreducerbara element i $k\left[X\right]$ , för ett fält $k$ . Det faktum att $\mathbb {Z}$ är en UFD kan sägas mer elementärt genom att säga att vilket naturligt tal som helst kan dekomponeras unikt som produkt av potenser av primtal. Det är också känt som aritmetikens grundsats .

Ett element $a$ är ett primtal element om närhelst $a$ delar en produkt $bc$ , $a$ delar $b$ eller $c$ . I en domän innebär att vara prime att vara irreducerbar. Det omvända är sant i en unik faktoriseringsdomän, men falsk i allmänhet.

Faktorringen

Definitionen av ideal är sådan att "dividing" $I$ "ut" ger en annan ring, faktorringen $R$ / $I$ : det är uppsättningen av coset av ${\ displaystyle I}$ tillsammans med operationerna

$$\left(a+I\right)+\left(b+I\right)=\ left(a+b\right)+I$$

och $\left(a+I\right)\left(b+I\right)=ab +I$ . Till exempel, ringen $\mathbb {Z} /n\mathbb {Z}$ (även betecknad $\mathbb {Z} _{n}$ ), där $n$ är ett heltal, är ringen av heltal modulo $n$ . Det är grunden för modulär aritmetik .

Ett ideal är lämpligt om det är strikt mindre än hela ringen. Ett ideal som inte strikt ingår i något egentligt ideal kallas maximal . En ideal $m$ är maximal om och endast om $R$ / $m$ är ett fält. Förutom nollringen har vilken ring som helst (med identitet) minst ett maximalt ideal; detta följer av Zorns lemma .

Noetherian ringar

Huvudartikel: Noetherian ring

En ring kallas Noetherian (till ära av Emmy Noether , som utvecklade detta koncept) om varje stigande kedja av ideal

$$0\subseteq I_{0}\ subseteq I_{1}\subseteq \dots \subseteq I_{n}\subseteq I_{n+1}\dots$$

blir stationär, dvs blir konstant bortom något index $n$ . På motsvarande sätt genereras vilket ideal som helst av ändligt många element, eller likväl ekvivalenta, submoduler av ändligt genererade moduler genereras ändligt.

Att vara Noetherian är ett mycket viktigt ändlighetstillstånd, och tillståndet bevaras under många operationer som ofta förekommer i geometrin. Till exempel, om $R$ är Noetherian, så är polynomringen $R\left[X_{1},X_{2},\ också prickar ,X_{n}\right]$ (genom Hilberts grundsats ), valfri lokalisering $S^{-1}R$ , och även valfri faktorring $R$ / ${\ displaystil I}$ .

Alla icke-noeteriska ringar $R$ är föreningen av dess noeteriska underringar. Detta faktum, känt som Noetherian approximation, tillåter utvidgning av vissa satser till icke-Noetherian ringar.

Artinian ringar

En ring kallas Artinian (efter Emil Artin ), om varje nedåtgående kedja av ideal

$$R\supseteq I_{0}\supseteq I_{1} \supseteq \dots \supseteq I_{n}\supseteq I_{n+1}\dots$$

blir stationär så småningom. Trots att de två tillstånden verkar symmetriska är Noetherian-ringar mycket mer allmänna än Artinian-ringar. Till exempel $\mathbb {Z}$ Noetherian, eftersom varje ideal kan genereras av ett element, men inte artinian, eftersom kedjan

$$\mathbb {Z} \supsetneq 2\mathbb {Z} \supsetneq 4\mathbb {Z} \supsetneq 8\mathbb {Z} \dots$$

visas. I själva verket, enligt Hopkins-Levitzki-satsen , är varje artinisk ring Noetherian. Mer exakt kan Artinian-ringar karakteriseras som Noether-ringarna vars Krull-dimension är noll.

Spektrum av en kommutativ ring

Främsta ideal

Huvudartikel: Prime ideal

Som nämndes ovan är $\mathbb {Z}$ en unik faktoriseringsdomän . Detta är inte sant för mer allmänna ringar, som algebraister insåg på 1800-talet. Till exempel i

$$\mathbb {Z} \left[{\sqrt {-5}}\right]$$

det finns två genuint distinkta sätt att skriva 6 som en produkt:

$$6=2\cdot 3=\left(1+{\sqrt {-5}}\right)\left(1-{\sqrt {-5}}\right).$$

Primära ideal, i motsats till primära element, ger ett sätt att kringgå detta problem. Ett primideal är ett egentligt (dvs strikt inkluderat i $R$ ) ideal $p$ så att när produkten $ab$ av två ringelement $a$ och $b$ är i $p,$ minst ett av de två elementen finns redan i $s.$ (Den motsatta slutsatsen gäller för alla ideal, per definition.) Så, om ett primideal är principiellt, genereras det på samma sätt av ett primtal. Men i ringar som $\mathbb {Z} \left[{\sqrt {-5}}\right],$ behöver inte primideal vara principiella. Detta begränsar användningen av primära element i ringteori. En hörnsten i algebraisk talteori är dock det faktum att i vilken Dedekind-ring som helst (som inkluderar $\mathbb {Z} \left[{\sqrt {-5}}\right]$ och mer generellt sett sönderfaller ringen av heltal i ett talfält ) vilket ideal som helst (som det som genereras av 6) unikt som en produkt av primärideal.

Alla maximala ideal är ett primideal eller, kortare, är prime. Dessutom är en ideal $I$ primtal om och endast om faktorringen $R/I$ är en integrerad domän. Att bevisa att ett ideal är primtal, eller motsvarande att en ring inte har några nolldelare kan vara mycket svårt. Ytterligare ett sätt att uttrycka detsamma är att säga att komplementet R $\displaystyle R\setminus p}$ är multiplikativt sluten. Lokaliseringen $\left(R\setminus p\right)^{-1}R$ är tillräckligt viktig för att ha sin egen notation: $R_{p}$ . Denna ring har bara ett maximalt ideal, nämligen $pR_{p}$ . Sådana ringar kallas lokala .

Spektrum

Huvudartikel: Spektrum av en ring

Spec ( Z ) innehåller en punkt för nollidealet. Stängningen av denna punkt är hela utrymmet. De återstående punkterna är de som motsvarar ideal ( p ), där p är ett primtal. Dessa punkter är stängda.

Spektrum för en ring $R$ , betecknat med ${\displaystyle {\text{Spec}}\ R} ,$ är mängden av alla primideal för $R$ . Den är utrustad med en topologi, Zariski-topologin , som återspeglar de algebraiska egenskaperna hos $R$ : en bas för öppna delmängder ges av

$$D\left(f\right)=\left\{p\in {\text{Spec}}\ R,f\not \in p\right\}} , där f {\displaystyle f$$

är $ringelement$ . Genom att tolka $f$ som en funktion som tar värdet f mod p (dvs. bilden av f i restfältet R / p ), är denna delmängd den plats där f är icke-noll. Spektrumet preciserar också intuitionen att lokalisering och faktorringar är komplementära: de naturliga kartorna R → Rf och R → R / fR motsvarar, efter att ha försett spektra för ringarna i fråga med deras Zariski-topologi, komplementära _öppna och slutna nedsänkningar respektive. Även för grundläggande ringar, som illustreras för R = Z till höger, är Zariski-topologin helt annorlunda än den på uppsättningen av reella tal.

Spektrumet innehåller uppsättningen av maximala ideal, som ibland betecknas mSpec ( R ). För ett algebraiskt slutet fält k , är mSpec (k[ T ₁ , ..., T _n ] / ( f ₁ , ..., f _m )) i bijektion med mängden

{ x =( x ₁ , ..., x _n ) ∊ k ⁿ

Maximala ideal återspeglar således de geometriska egenskaperna hos lösningsuppsättningar av polynom, vilket är en initial motivation för studiet av kommutativa ringar. Men övervägandet av icke-maximala ideal som en del av de geometriska egenskaperna hos en ring är användbart av flera skäl. Till exempel motsvarar de minimala primidealen (dvs de som inte strikt innehåller mindre) de irreducerbara komponenterna i Spec R . För en Noetherian ring R har Spec R endast ändligt många irreducerbara komponenter. Detta är en geometrisk omformulering av primär nedbrytning , enligt vilken vilket ideal som helst kan dekomponeras som en produkt av ändligt många primära ideal . Detta faktum är den ultimata generaliseringen av nedbrytningen till främsta ideal i Dedekind-ringar.

Affina system

Begreppet ett spektrum är den gemensamma grunden för kommutativ algebra och algebraisk geometri . Algebraisk geometri fortsätter genom att förse Spec R med en bunt ${\mathcal {O}}$ (en entitet som samlar funktioner definierade lokalt, dvs på olika öppna delmängder). Datumet för utrymmet och kärven kallas ett affint schema . Givet ett affint schema kan den underliggande ringen R återställas som de globala sektionerna av ${\mathcal {O}}$ . Dessutom är denna en-till-en-överensstämmelse mellan ringar och affina scheman också kompatibel med ringhomomorfismer: vilken f : R → S som helst ger upphov till en kontinuerlig karta i motsatt riktning

Spec S → Spec R , q ↦ f ⁻¹ ( q ), dvs alla primideal för S mappas till sin förbild under f , vilket är ett primideal av R .

Den resulterande ekvivalensen av de två nämnda kategorierna återspeglar lämpligen algebraiska egenskaper hos ringar på ett geometriskt sätt.

I likhet med det faktum att grenrör ges lokalt av öppna delmängder av Rn , är affina scheman lokala modeller för ^scheman , som är föremål för studier i algebraisk geometri. Därför härrör flera föreställningar om kommutativa ringar från geometrisk intuition.

Dimensionera

Huvudartikel: Krull dimension

Krulldimensionen (eller dimensionen ) dim R för en ring R mäter "storleken" på en ring genom att, grovt sett, räkna oberoende element i R . Dimensionen av algebran över ett fält k kan axiomatiseras med fyra egenskaper:

• Dimensionen är en lokal egenskap: dim R = sup _{p ∊ Spec R} dim R _p .
• Dimensionen är oberoende av nilpotenta element: om I ⊆ R är nilpotent så är dim R = dim R / I .
• Dimensionen förblir konstant under en finit förlängning: om S är en R -algebra som ändligt genereras som en R -modul, då dim S = dim R .
• Dimensionen kalibreras med dim k [ X ₁ , ..., X _n ] = n . Detta axiom motiveras av att betrakta polynomringen i n variabler som en algebraisk analog till n -dimensionellt rymd .

Dimensionen definieras, för valfri ring R , som det högsta av längderna n av kedjor av prime ideal

₀ p ⊊ p ₁ ⊊ ... ⊊ p _n .

Till exempel är ett fält nolldimensionellt, eftersom det enda primidealet är nollidealet. Heltalen är endimensionella, eftersom kedjor har formen (0) ⊊ ( p ), där p är ett primtal . För icke-noeteriska ringar, och även icke-lokala ringar, kan dimensionen vara oändlig, men noeteriska lokala ringar har en ändlig dimension. Bland de fyra axiomen ovan är de två första elementära konsekvenserna av definitionen, medan de återstående två hänger på viktiga fakta i kommutativ algebra , gå -upp-satsen och Krulls huvudsakliga idealsats .

Ringhomomorfismer

Huvudartikel: Ringhomomorfism

En ringhomomorfism eller, mer vardagligt, helt enkelt en karta , är en karta f : R → S sådan att

f ( a + b ) = f ( a ) + f ( b ), f ( ab ) = f ( a ) f ( b ) och f (1) = 1.

Dessa villkor säkerställer f (0) = 0. På samma sätt som för andra algebraiska strukturer är en ringhomomorfism alltså en karta som är kompatibel med strukturen hos de aktuella algebraiska objekten. I en sådan situation kallas S också en R -algebra, genom att förstå att s i S kan multipliceras med någon r av R , genom att sätta

r · s := f ( r ) · s .

Kärnan och bilden av f definieras av ker ( f ) = { r ∈ R , f ( r ) = 0} och im ( f ) = f ( R ) = { f ( r ), r ∈ R } . Kärnan är ett ideal för R , och bilden är en subring av S.

En ringhomomorfism kallas en isomorfism om den är bijektiv. Ett exempel på en ringisomorfism, känd som den kinesiska restsatsen , är

$$\mathbf {Z} /n=\bigoplus _{i=0}^{k}\mathbf {Z} /p_{i}$$

där n = p ₁ p ₂ ... p _k är en produkt av parvis distinkta primtal .

Kommutativa ringar, tillsammans med ringhomomorfismer, bildar en kategori . Ringen Z är det initiala objektet i denna kategori, vilket betyder att för varje kommutativ ring R finns en unik ringhomomorfism Z → R . Med hjälp av denna karta kan ett heltal n betraktas som ett element av R . Till exempel binomialformeln

$$(a+b)^{n}=\summa _{k=0}^{n}{\binom { n}{k}}a^{k}b^{nk}$$

som är giltigt för alla två element a och b i vilken kommutativ ring R som helst , förstås i denna mening genom att tolka de binomiala koefficienterna som element i R med användning av denna karta.

Den universella egenskapen för S ⊗ _R T anger att för två valfria kartor S → W och T → W som får den yttre fyrkanten att pendla, finns det en unik karta S ⊗ _R T → W som gör att hela diagrammet pendlar.

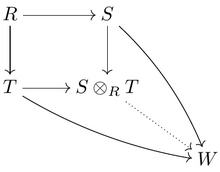
Givet två R -algebror S och T , deras tensorprodukt

S ⊗ _R T

är återigen en kommutativ R -algebra. I vissa fall kan tensorprodukten tjäna till att hitta en T -algebra som relaterar till Z som S relaterar till R . Till exempel,

R [ X ] ⊗ _R T = T [ X ].

Ändlig generation

En R -algebra S kallas ändligt genererad (som en algebra) om det finns ändligt många element s ₁ , ..., s _n så att vilket element av s som helst kan uttryckas som ett polynom i s _i . På motsvarande sätt S isomorft till

R [ Ti , ..., _Tn ] / I _.

Ett mycket starkare villkor är att S ändligt genereras som en R -modul , vilket betyder att vilket s som helst kan uttryckas som en R -linjär kombination av någon ändlig mängd s ₁ , ..., s _n .

Lokala ringar

En ring kallas lokal om den bara har ett enda maximalt ideal, betecknat med m . För varje (inte nödvändigtvis lokal) ring R , lokaliseringen

R _sid

vid ett utmärkt ideal är p lokalt. Denna lokalisering återspeglar de geometriska egenskaperna hos Spec R "runt p ". Flera föreställningar och problem i kommutativ algebra kan reduceras till fallet när R är lokal, vilket gör lokala ringar till en särskilt djupt studerad klass av ringar. Restfältet för R definieras som

k = R / m .

Varje R -modul M ger ett k -vektorutrymme givet av M / mM . Nakayamas lemma visar att denna passage bevarar viktig information: en ändligt genererad modul M är noll om och endast om M / mM är noll.

Regelbundna lokala ringar

Kubikplanets kurva (röd) definierad av ekvationen y ² = x ² ( x + 1 ) är singular vid origo, dvs ringen k [ x , y ] / y ² − x ² ( x + 1 ), är inte en vanlig ring. Tangentkonen (blå) är en förening av två linjer, vilket också återspeglar singulariteten.

K - vektorutrymmet m / m ² är en algebraisk inkarnation av det kotangenta rummet . Informellt kan elementen i m ses som funktioner som försvinner vid punkten p , medan m ² innehåller de som försvinner med ordningen minst 2. För varje Noetherisk lokal ring R är olikheten

dim _k m / m ² ≥ dim R

stämmer, vilket återspeglar idén att cotangensen (eller motsvarande tangenten) rymden har åtminstone dimensionen av rymden Spec R . Om likheten gäller i denna uppskattning kallas R en vanlig lokal ring . En Noethersk lokal ring är regelbunden om och endast om ringen (som är ringen av funktioner på tangentkonen )

$$\bigoplus _{n}m^{n}/m^{n+1}$$

är isomorft till en polynomring över k . I stort sett liknar vanliga lokala ringar något polynomringar. Vanliga lokala ringar är UFD:s.

Diskreta värderingsringar är utrustade med en funktion som tilldelar ett heltal till varje element r . Detta nummer, som kallas värderingen av r , kan informellt ses som en noll- eller polordning av r . Diskreta värderingsringar är just de endimensionella vanliga lokala ringarna. Till exempel är ringen av groddar av holomorfa funktioner på en Riemann- yta en diskret värderingsring.

Kompletta korsningar

Den vridna kuben (grön) är en mängdteoretisk fullständig skärning, men inte en fullständig korsning.

Enligt Krulls principiella idealsats , ett grundläggande resultat i dimensionsteorin om ringar , dimensionen av

R = k [ T ₁ , ..., Tr ] / ( f ₁ , ..., f _{n )}

är åtminstone r − n . En ring R kallas en komplett skärningsring om den kan presenteras på ett sätt som uppnår denna minimala gräns. Denna uppfattning studeras också mest för lokala ringar. Varje vanlig lokal ring är en komplett skärningsring, men inte omvänt.

En ring R är en mängdteoretisk fullständig skärning om den reducerade ringen associerad med R , dvs den som erhålls genom att dela ut alla nilpotenta element, är en fullständig skärning. Från och med 2017 är det i allmänhet okänt huruvida kurvor i tredimensionellt rymd är mängdteoretiska fullständiga skärningar.

Cohen–Macaulay ringer

Djupet av en lokal ring R är antalet element i någon (eller, som kan visas, vilken som helst) maximal regelbunden sekvens, dvs. en sekvens a ₁ , ..., a _n ∈ m så att alla a _i är icke -nolldelare in

R / ( a ₁ , ..., a _{i −1} ).

För alla lokala Noetherian ring, ojämlikheten

djup ( R ) ≤ dim ( R )

håller. En lokal ring där jämlikhet äger rum kallas en Cohen–Macaulay-ring . Lokala kompletta skärningsringar, och a fortiori, vanliga lokala ringar är Cohen–Macaulay, men inte omvänt. Cohen–Macaulay kombinerar önskvärda egenskaper hos vanliga ringar (såsom egenskapen att vara universellt kontaktledningsringar , vilket innebär att (sam)dimensionen av primtal är väluppfostrad), men är också mer robusta undertagningskvoter än vanliga lokala ringar.

Konstruera kommutativa ringar

Det finns flera sätt att konstruera nya ringar av givna. Syftet med sådana konstruktioner är ofta att förbättra vissa egenskaper hos ringen för att göra den mer lättförståelig. kallas en integraldomän som är integrerat stängd i sitt bråkfält normal . Detta är en önskvärd egenskap, till exempel är varje normal endimensionell ring nödvändigtvis regelbunden . Att göra en ring normal kallas normalisering .

Slutföranden

0 Om I är ett ideal i en kommutativ ring R , bildar krafterna av I topologiska grannskap där R kan ses som en topologisk ring . Denna topologi kallas I -adisk topologi . R kan sedan kompletteras med avseende på denna topologi. Formellt In ^är I -adic-kompletteringen den omvända gränsen för ringarna R / . Till exempel, om k är ett fält, k [[ X ] ], är den formella potensserieringen i en variabel över k , den I -adiska kompletteringen av k [ X ] där I är det huvudsakliga idealet som genereras av X. Denna ring fungerar som en algebraisk analog till skivan. Analogt är ringen av p -adiska heltal fullbordandet av Z med avseende på huvudidealet ( p ). Varje ring som är isomorf till sin egen komplettering kallas komplett .

Kompletta lokala ringar uppfyller Hensels lemma , som grovt sett tillåter utvidgning av lösningar (av olika problem) över restfältet k till R .

Homologiska föreställningar

Flera djupare aspekter av kommutativa ringar har studerats med metoder från homologisk algebra . Hochster (2007) listar några öppna frågor inom detta område av aktiv forskning.

Projektiva moduler och Ext-funktioner

Projektiva moduler kan definieras som direkta summeringar av fria moduler. Om R är lokal är varje ändligt genererad projektiv modul faktiskt gratis, vilket ger innehåll till en analogi mellan projektiva moduler och vektorbuntar . Quillen –Suslin-satsen hävdar att varje ändligt genererad projektiv modul över k [ T ₁ , ..., T _n ] ( k a field) är fri, men i allmänhet skiljer sig dessa två begrepp. En lokal noeterisk ring är regelbunden om och endast om dess globala dimension är finit, säg n , vilket betyder att varje ändligt genererad R -modul har en upplösning av projektiva moduler med längd som mest n .

Beviset för detta och andra relaterade uttalanden är beroende av användningen av homologiska metoder, såsom Ext-funktorn . Denna funktor är den härledda funktorn av funktorn

Hom _R ( M , -).

Den senare funktorn är exakt om M är projektiv, men inte annars: för en surjektiv karta E → F av R -moduler behöver en karta M → F inte sträcka sig till en karta M → E . De högre Ext-funktionerna mäter Hom-funktorns oexakthet. Vikten av denna standardkonstruktion i homologiska algebrastammar kan ses av det faktum att en lokal Noetherian ring R med restfält k är regelbunden om och endast om

Ext ⁿ ( k , k )

försvinner för alla tillräckligt stora n . Dessutom växer dimensionerna för dessa Ext-grupper, kända som Betti-tal , polynomiellt i n om och endast om R är en lokal komplett skärningsring . Ett nyckelargument i sådana överväganden är Koszul-komplexet , vilket ger en explicit fri upplösning av restfältet k i en lokal ring R i termer av en regelbunden sekvens.

Flathet

Tensorprodukten är en annan icke-exakt funktion som är relevant i sammanhanget med kommutativa ringar: för en allmän R -modul M , funktorn

M ⊗ _R −

är bara rätt exakt. Om det är exakt kallas M platt . Om R är lokal är varje ändligt presenterad platt modul fri från finit rang, och därmed projektiv. Trots att den definieras i termer av homologisk algebra har platthet djupgående geometriska implikationer. Till exempel, om en R -algebra S är platt, dimensionerna på fibrerna

S / pS = S ⊗ _R R / p

(för primideal p i R ) har den "förväntade" dimensionen, nämligen dim S − dim R + dim ( R / p ).

Egenskaper

Enligt Wedderburns teorem är varje finit divisionsring kommutativ och därför ett finit fält . Ett annat villkor som säkerställer kommutativitet för en ring, på grund av Jacobson , är följande: för varje element r av R finns det ett heltal n > 1 så att r ⁿ = r . Om r ² = r för varje r kallas ringen Boolesk ring . Mer allmänna villkor som garanterar kommutativitet hos en ring är också kända.

Generaliseringar

Graderade kommutativa ringar

Ett par byxor är en samordning mellan en cirkel och två osammanhängande cirklar. Kobordismklasser, med den kartesiska produkten som multiplikation och disjunkt förening som summan, bildar kobordismringen .

En graderad ring R = ⨁ _{i ∊ Z} R _i kallas graderad kommutativ om, för alla homogena element a och b ,

ab = (−1) ^{deg a ⋅ deg b} ba .

Om R _i är förbundna med differentialer ∂ så att en abstrakt form av produktregeln gäller , dvs.

∂( ab ) = ∂( a ) b + (−1) ^{grader a} ∂( b ),

R kallas en kommutativ differentiell graderad algebra (cdga). Ett exempel är komplexet av differentialformer på ett grenrör , med multiplikationen som ges av den yttre produkten , är en cdga. Kohomologin för en cdga är en graderad kommutativ ring, ibland kallad kohomologiringen . Ett brett spektrum av exempel på graderade ringar uppstår på detta sätt. Till exempel Lazard-ringen ringen av kobordismklasser av komplexa grenrör.

En graderad kommutativ ring med avseende på en gradering av Z /2 (i motsats till Z ) kallas en superalgebra .

Ett relaterat begrepp är en nästan kommutativ ring , vilket innebär att R filtreras på ett sådant sätt att den tillhörande graderade ringen

gr R := ⨁ F _i R / ⨁ F _{i −1} R

är kommutativ. Ett exempel är Weyl-algebra och mer allmänna ringar av differentialoperatorer .

Enkla kommutativa ringar

En enkel kommutativ ring är ett enkelt objekt i kategorin kommutativa ringar. De är byggstenar för (bindande) härledd algebraisk geometri . Ett närbesläktat men mer allmänt begrepp är E _∞ -ring .

Tillämpningar av de kommutativa ringarna

• Holomorfa funktioner
• Algebraisk K-teori
• Topologisk K-teori
• Delade maktstrukturer
• Witt vektorer
• Hecke algebra (används i Wiles bevis på Fermats sista sats )
• Fontaines period ringer
• Kluster algebra
• Konvolutionsalgebra (av en kommutativ grupp)
• Fréchet algebra

Se även

• Nästan ring , en viss generalisering av en kommutativ ring
• Delbarhet (ringteori) : nilpotent element , (ex. dubbla tal )
• Ideal och moduler: Radikal av ett ideal , Morita-ekvivalens
• Ringhomomorfismer : integralelement : Cayley–Hamilton-satsen , Integralt sluten domän , Krull-ringen , Krull–Akizuki-satsen , Mori–Nagata-satsen
• Primer: Primeradikal-lemma , Jacobson-radikal , Nilradical of a ring , Spektrum: Kompakt rymd , Ansluten ring , Differentialkalkyl över kommutativa algebror , Banach-Stensats
• Lokala ringar : Gorenstein lokal ring (används också i Wiles bevis på Fermats sista sats ): Dualitet (matematik), Eben Matlis ; Dualiseringsmodul , Popescus sats , Artin approximationssats .

Anteckningar

Citat

•   Christensen, Lars Winther; Striuli, Janet; Veliche, Oana (2010), "Growth in the minimal injective resolution of a local ring", Journal of the London Mathematical Society , Second Series, 81 (1): 24–44, arXiv : 0812.4672 , doi : 10.1112/jlms/jdp058 , S2CID 14764965
•    Eisenbud, David (1995), Kommutativ algebra. Med sikte på algebraisk geometri. , Graduate Texts in Mathematics , vol. 150, Berlin, New York: Springer-Verlag , ISBN 978-0-387-94268-1 , MR 1322960
• Hochster, Melvin (2007), "Homological conjectures, old and new", Illinois J. Math. , 51 (1): 151–169, doi : 10.1215/ijm/1258735330
•    Jacobson, Nathan (1945), "Structure theory of algebraic algebras of bounded degree", Annals of Mathematics , 46 (4): 695–707, doi : 10.2307/1969205 , ISSN 0003-486X , J92STOR 596
•   Lyubeznik, Gennady (1989), "A survey of problems and results on the number of defining equations", Representations, resolutions and intertwining numbers , s. 375–390, Zbl 0753.14001
•   Matsumura, Hideyuki (1989), Commutative Ring Theory , Cambridge Studies in Advanced Mathematics (2:a upplagan), Cambridge University Press , ISBN 978-0-521-36764-6
•   Pinter-Lucke, James (2007), "Kommutativitetsvillkor för ringar: 1950–2005", Expositiones Mathematicae , 25 (2): 165–174, doi : 10.1016/j.exmath.2006.07.001 , ISSN 06923-06923

Vidare läsning

• Atiyah, Michael ; Macdonald, IG (1969), Introduktion till kommutativ algebra , Addison-Wesley Publishing Co.
•   Balcerzyk, Stanisław; Józefiak, Tadeusz (1989), Commutative Noetherian and Krull rings , Ellis Horwood Series: Mathematics and its Applications, Chichester: Ellis Horwood Ltd., ISBN 978-0-13-155615-7
•   Balcerzyk, Stanisław; Józefiak, Tadeusz (1989), Dimension, multiplicitet och homologiska metoder , Ellis Horwood Series: Mathematics and its Applications., Chichester: Ellis Horwood Ltd., ISBN 978-0-13-155623-2
•   Kaplansky, Irving (1974), Kommutativa ringar (reviderad utg.), University of Chicago Press , MR 0345945
•    Nagata, Masayoshi (1975) [1962], Local rings , Interscience Tracts in Pure and Applied Mathematics, vol. 13, Interscience Publishers, s. xiii+234, ISBN 978-0-88275-228-0 , MR 0155856
• Zariski, Oscar ; Samuel, Pierre (1958–60), Commutative Algebra I, II , University series in Higher Mathematics, Princeton, NJ: D. van Nostrand, Inc. (Återtryckt 1975-76 av Springer som volymerna 28-29 av Graduate Texts in Mathematics. )