Riemann yta

Riemannyta för funktionen f ( z ) = √ z . De två horisontella axlarna representerar den reella och imaginära delen av z , medan den vertikala axeln representerar den reella delen av √ z . Den imaginära delen av √ z representeras av färgen på punkterna. För denna funktion är det också höjden efter att ha roterat diagrammet 180° runt den vertikala axeln.

Inom matematiken , särskilt i komplex analys , är en Riemann-yta en ansluten endimensionell komplex mångfald . Dessa ytor studerades först av och är uppkallade efter Bernhard Riemann . Riemann-ytor kan ses som deformerade versioner av det komplexa planet : lokalt nära varje punkt ser de ut som fläckar på det komplexa planet, men den globala topologin kan vara helt annorlunda. Till exempel kan de se ut som en sfär eller en torus eller flera ark limmade ihop.

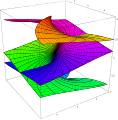
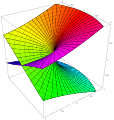
Huvudintresset för Riemann-ytor är att holomorfa funktioner kan definieras mellan dem. Riemann-ytor anses numera vara den naturliga miljön för att studera det globala beteendet hos dessa funktioner, särskilt flervärdiga funktioner som kvadratroten och andra algebraiska funktioner eller logaritmen .

Varje Riemann-yta är en tvådimensionell verklig analytisk mångfald (dvs. en yta ), men den innehåller mer struktur (specifikt en komplex struktur ) som behövs för en entydig definition av holomorfa funktioner. En tvådimensionell verklig grenrör kan förvandlas till en Riemann-yta (vanligtvis på flera olika sätt) om och bara om den är orienterbar och mätbar . Så sfären och torus tillåter komplexa strukturer, men Möbius-remsan , Klein-flaskan och det verkliga projektiva planet gör det inte.

Geometriska fakta om Riemann-ytor är så "fina" som möjligt, och de ger ofta intuition och motivation för generaliseringar till andra kurvor, grenrör eller varianter. Riemann -Roch-satsen är ett utmärkt exempel på detta inflytande.

Definitioner

Det finns flera motsvarande definitioner av en Riemann-yta.

En Riemann-yta X är ett sammankopplat komplext grenrör av komplex dimension ett. Detta betyder att X är ett anslutet Hausdorff-utrymme som är försett med en kartatlas till den öppna enhetsskivan i det komplexa planet : för varje punkt x ∈ X finns det en grannskap av x som är homeomorf till den öppna enhetsskivan i komplexet plan, och övergångskartorna mellan två överlappande sjökort måste vara holomorfa .
En Riemann-yta är ett orienterat grenrör av (verklig) dimension två – en tvåsidig yta – tillsammans med en konform struktur . Återigen betyder mångfaldigt att lokalt vid vilken punkt som helst x av X är rymden homeomorf till en delmängd av det verkliga planet. Tillägget "Riemann" betyder att X är försett med en ytterligare struktur som tillåter vinkelmätning på grenröret, nämligen en ekvivalensklass av så kallade Riemanniska metriker . Två sådana mätvärden anses vara likvärdiga om vinklarna de mäter är desamma. Att välja en ekvivalensklass av mått på X är det ytterligare datumet för den konforma strukturen.

En komplex struktur ger upphov till en konform struktur genom att välja den euklidiska standardmetriken som ges på det komplexa planet och transportera den till X med hjälp av diagrammen. Att visa att en konform struktur bestämmer en komplex struktur är svårare.

Exempel

Riemann-sfären.

En torus.

Det komplexa planet C är den mest grundläggande Riemann-ytan. Kartan f ( z ) = z (identitetskartan) definierar ett diagram för C , och { f } är en atlas för C. Kartan g ( z ) = z ^* (den konjugerade kartan) definierar också ett diagram på C och { g } är en atlas för C . Diagrammen f och g är inte kompatibla, så detta ger C två distinkta Riemann-ytstrukturer. I själva verket, givet en Riemann-yta X och dess atlas A , är den konjugatatlas B = { f ^* : f ∈ A } aldrig kompatibel med A , och ger X en distinkt, inkompatibel Riemann-struktur.
På ett analogt sätt kan varje icke-tom öppen delmängd av det komplexa planet ses som en Riemann-yta på ett naturligt sätt. Mer generellt är varje icke-tom öppen delmängd av en Riemann-yta en Riemann-yta.
Låt S = C ∪ {∞} och låt f ( z ) = z där z är i S \ {∞} och g ( z ) = 1 / z där z är i S \ {0} och 1/∞ är definierad till vara 0. Då är f och g diagram, de är kompatibla, och { f , g } är en atlas för S , vilket gör S till en Riemannyta. Denna speciella yta kallas Riemann-sfären eftersom den kan tolkas som att den lindar det komplexa planet runt sfären. Till skillnad från det komplexa planet är det kompakt .
Teorin om kompakt Riemann-yta s kan visas vara ekvivalent med den för projektiva algebraiska kurvor som är definierade över de komplexa talen och icke-singular. Till exempel torus C /( Z + τ Z ), där τ är ett komplext icke-reellt tal, via Weierstrass elliptiska funktion associerad med gittret Z + τ Z , en elliptisk kurva som ges av en ekvation
y ² = x ³ + ax + b .

Tori är de enda Riemann-ytorna av släktet ett, ytor av högre släkten g tillhandahålls av de hyperelliptiska ytorna

y ² = P ( x ),
där P är ett komplext polynom med grad 2 g + 1.
Alla kompakta Riemann-ytor är algebraiska kurvor eftersom de kan bäddas in i vissa $\mathbb {CP} ^{n}$ . Detta följer av Kodairas inbäddningssats och det faktum att det finns en positiv linjebunt på vilken komplex kurva som helst.
Viktiga exempel på icke-kompakta Riemann-ytor tillhandahålls genom analytisk fortsättning .

f ( z ) = båge z
f ( z ) = log z
f ( z ) = z ^1/2
f ( z ) = z ^1/3
f ( z ) = z ^1/4

Ytterligare definitioner och egenskaper

Som med vilken karta som helst mellan komplexa grenrör, kallas en funktion f : M → N mellan två Riemann-ytor M och N holomorf om för varje diagram g i M - atlasen och varje diagram h i N -atlasen , kartan h ∘ f ∘ g ⁻¹ är holomorf (som en funktion från C till C ) varhelst den definieras. Sammansättningen av två holomorfa kartor är holomorfisk. De två Riemannytorna M och N kallas biholomorfa (eller konformt ekvivalenta för att betona den konforma synvinkeln) om det finns en bijektiv holomorf funktion från M till N vars invers också är holomorf (det visar sig att det senare tillståndet är automatiskt och kan därför utelämnas). Två konformt ekvivalenta Riemann-ytor är för alla praktiska ändamål identiska.

Orienterbarhet

Varje Riemann-yta, som är ett komplext grenrör, är orienterbart som ett riktigt grenrör. För komplexa diagram f och g med övergångsfunktion h = f ( g ⁻¹ ( z )), kan h betraktas som en karta från en öppen uppsättning av R ² till R ² vars Jacobian i en punkt z bara är den verkliga linjära kartan ges genom multiplikation med det komplexa talet h '( z ). Emellertid är den reella determinanten för multiplikation med ett komplext tal α lika med | α | ² , så jakobian av h har positiv determinant. Följaktligen är den komplexa atlasen en orienterad atlas.

Funktioner

Varje icke-kompakt Riemann-yta tillåter icke-konstanta holomorfa funktioner (med värden i C ). Faktum är att varje icke-kompakt Riemann-yta är en Stein-grenrör .

Däremot på en kompakt Riemann-yta X är varje holomorf funktion med värden i C konstant på grund av maximiprincipen . Det finns dock alltid icke-konstanta meromorfa funktioner (holomorfa funktioner med värden i Riemann-sfären C ∪ {∞}). Närmare bestämt funktionsfältet för X en finit förlängning av C ( t ), funktionsfältet i en variabel, dvs vilka två meromorfa funktioner som helst är algebraiskt beroende. Detta uttalande generaliserar till högre dimensioner, se Siegel (1955) . Meromorfa funktioner kan ges ganska explicit, i termer av Riemann theta-funktioner och Abel–Jacobi-kartan över ytan.

Analytisk vs. algebraisk

Förekomsten av icke-konstanta meromorfa funktioner kan användas för att visa att varje kompakt Riemann yta är en projektiv variation , dvs kan ges av polynomekvationer inuti ett projektivt utrymme . Det kan faktiskt visas att varje kompakt Riemann-yta kan bäddas in i komplext projektivt 3-utrymme . Detta är ett överraskande teorem: Riemann-ytor ges av lokalt lappande sjökort. Om ett globalt villkor, nämligen kompakthet, läggs till, är ytan nödvändigtvis algebraisk. Denna egenskap hos Riemann-ytor gör att man kan studera dem med antingen analytisk eller algebraisk geometri . Motsvarande påstående för högredimensionella objekt är falskt, dvs det finns kompakta komplexa 2-grenrör som inte är algebraiska. Å andra sidan är varje projektiv komplex mångfald nödvändigtvis algebraisk, se Chows sats .

Som ett exempel, betrakta torusen T := C /( Z + τ Z ). Weierstrass -funktionen $\wp _{\tau }(z)$ som hör till gittret Z + τ Z är en meromorf funktion på T . Denna funktion och dess derivata $\wp _{\tau }'(z)$ genererar funktionsfältet för T . Det finns en ekvation

[\wp '(z)]^{2}=4[\wp (z )]^{3}-g_{2}\wp (z)-g_{3},

där koefficienterna g ₂ och g ₃ beror på τ, vilket ger en elliptisk kurva E _τ i betydelsen algebraisk geometri. Att vända detta åstadkoms av j-invarianten j ( E ), som kan användas för att bestämma τ och därmed en torus.

Klassificering av Riemann-ytor

Uppsättningen av alla Riemann-ytor kan delas in i tre delmängder: hyperboliska, paraboliska och elliptiska Riemann-ytor. Geometriskt motsvarar dessa ytor med negativ, försvinnande eller positiv konstant tvärsnittskrökning . Det vill säga att varje ansluten Riemann-yta $X$ tillåter en unik komplett 2-dimensionell verklig $, {\displaystyle -1,0}$ -metrik med konstant krökning lika med eller $1$ som tillhör konform klass av Riemann-mått bestäms av dess struktur som en Riemann-yta. Detta kan ses som en konsekvens av att det finns isotermiska koordinater .

I komplexa analytiska termer säger Poincaré-Koebes uniformeringssats (en generalisering av Riemanns kartläggningssats ) att varje enkelt sammankopplad Riemann-yta är konformt ekvivalent med något av följande:

Riemann-sfären ${\displaystyle {\widehat {\mathbf {C} }}:=\mathbf {C} \cup \{\infty \}} ,$ som är isomorft till $\mathbf {P} ^{1}(\mathbf {C} )$ ;
Det komplexa planet $\mathbf {C}$ ;
Den öppna disken $\mathbf {D} :=\{z\in \mathbf {C} :|z|<1\}$ som är isomorft till det övre halvplanet $\mathbf {H} :=\{z\in \mathbf {C} :\mathrm {Im} (z)>0\}$ .

En Riemann-yta är elliptisk, parabolisk eller hyperbolisk beroende på om dess universalhölje är isomorft till ${\displaystyle \mathbf {P} ^{1}(\mathbf {C} )} ,$ C $\displaystyle \mathbf {C} }$ eller $\mathbf {D}$ . Elementen i varje klass medger en mer exakt beskrivning.

Elliptiska Riemann-ytor

Riemann-sfären $\mathbf {P} ^{1}(\mathbf {C} )$ är det enda exemplet, eftersom det inte finns någon grupp som verkar på den genom biholomorfa transformationer fritt och korrekt diskontinuerligt och så vilken Riemann-yta som helst vars universella hölje är isomorft till $\mathbf {P} ^{1}(\mathbf {C} )$ måste själv vara isomorft till den.

Paraboliska Riemann-ytor

Om $X$ är en Riemann-yta vars universella hölje är isomorft till det komplexa planet $\mathbf {C}$ så är det isomorft till en av följande ytor:

$\mathbf {C}$ sig själv;
Kvotienten $\mathbf {C} /\mathbf {Z}$ ;
En kvot $\mathbf {C} /(\mathbf {Z} +\mathbf {Z} \tau )$ där $\tau \in \mathbf {C }$ med $\mathrm {Im} (\tau )>0$ .

Topologiskt finns det bara tre typer: planet, cylindern och torus . Men medan den (paraboliska) Riemanns ytstrukturen i de två förstnämnda fallet är unik, ger en variation av parametern $\tau$ i det tredje fallet icke-isomorfa Riemann-ytor. Beskrivningen av parametern $\tau$ ger Teichmüller-utrymmet av "markerade" Riemann-ytor (utöver Riemann-ytstrukturen lägger man till topologiska data för en "markering", vilket kan ses som en fixerad homeomorfism till torus). För att erhålla det analytiska modulutrymmet (att glömma markeringen) tar man kvoten av Teichmüller-rymden av kartläggningsklassgruppen . I detta fall är det den modulära kurvan .

Hyperboliska Riemann-ytor

I de återstående fallen är $X$ en hyperbolisk Riemann-yta, som är isomorf till en kvot av det övre halvplanet av en fuchsisk grupp (detta kallas ibland en fuchsisk modell för ytan). Den topologiska typen av $X$ kan vara vilken orienterbar yta som helst förutom torus och sfär .

Ett fall av särskilt intresse är när $X$ är kompakt. Sedan beskrivs dess topologiska typ av dess släkte $g\geq 2$ . Dess Teichmüller-utrymme och modulutrymme är $6g-6$ -dimensionella. En liknande klassificering av Riemann-ytor av finit typ (det vill säga homeomorfa till en sluten yta minus ett ändligt antal punkter) kan ges. Men i allmänhet är modulutrymmet för Riemann-ytor av oändlig topologisk typ för stort för att tillåta en sådan beskrivning.

Kartor mellan Riemanns ytor

Den geometriska klassificeringen återspeglas i kartor mellan Riemann-ytor, som beskrivs i Liouvilles sats och Little Picard-satsen : kartor från hyperbolisk till parabolisk till elliptisk är lätt, men kartor från elliptisk till parabolisk eller parabolisk till hyperbolisk är mycket begränsade (i själva verket generellt konstanta !). Det finns inneslutningar av skivan i planet i sfären: $\Delta \subset \mathbf {C} \subset {\widehat {\mathbf {C} }},$ men vilken holomorf som helst karta från sfären till planet är konstant, varje holomorf karta från planet till enhetsskivan är konstant (Liouvilles sats), och i själva verket är varje holomorf karta från planet in i planet minus två punkter konstant (Lilla Picards sats)!

Punkterade sfärer

Dessa påståenden förtydligas genom att överväga typen av Riemann-sfär ${\widehat {\mathbf {C} }}$ med ett antal punkteringar. Utan några punkteringar är det Riemann-sfären som är elliptisk. Med en punktering, som kan placeras i oändlighet, är det det komplexa planet, som är paraboliskt. Vid två punkteringar är det det punkterade planet alternativt ring eller cylinder, som är parabolisk. Med tre eller fler punkteringar är det hyperboliskt – jämför ett par byxor . Man kan mappa från en punktering till två, via den exponentiella kartan (som är hel och har en väsentlig singularitet i oändligheten, alltså inte definierad vid oändlighet, och missar noll och oändlighet), men alla kartor från nollpunkteringar till en eller flera, eller en eller två punkteringar till tre eller fler är konstanta.

Förgrenade täckande utrymmen

Fortsatt i denna anda kan kompakta Riemann-ytor kartläggas till ytor av lägre släkte, men inte till högre släkt, förutom som konstanta kartor. Detta beror på att holomorfa och meromorfa kartor beter sig lokalt som $z\mapsto z^{n},$ så icke-konstanta kartor är förgrenade täckande kartor , och för kompakta Riemann-ytor är dessa begränsade av Riemann– Hurwitz-formel i algebraisk topologi , som relaterar Euler-karaktäristiken för ett utrymme och ett förgrenat lock.

Till exempel är hyperboliska Riemann-ytor förgrenade täckande utrymmen i sfären (de har icke-konstanta meromorfa funktioner), men sfären täcker inte eller på annat sätt mappar till högre genusytor, förutom som en konstant.

Isometrier av Riemann-ytor

Isometrigruppen för en enhetlig Riemann-yta (motsvarande den konforma automorfismgruppen ) återspeglar dess geometri:

släkte 0 – sfärens isometrigrupp är Möbiusgruppen av projektiva transformationer av den komplexa linjen,
planets isometrigrupp är undergruppen som fixerar oändligheten, och i det punkterade planet är undergruppen som lämnar invariant mängden som endast innehåller oändlighet och noll: antingen fixerar båda dem eller byter ut dem (1/ z ).
isometrigruppen i det övre halvplanet är den verkliga Möbiusgruppen; detta är konjugerat till diskens automorfismgrupp.
släkte 1 – isometrigruppen för en torus är i allmänhet översättningar (som en Abelisk variant ), även om det kvadratiska gittret och det hexagonala gittret har additionssymmetrier från rotation med 90° och 60°.
För släktet g ≥ 2 är isometrigruppen ändlig och har ordningen högst 84( g −1), enligt Hurwitzs automorfissats ; ytor som inser denna gräns kallas Hurwitz-ytor.
Det är känt att varje ändlig grupp kan realiseras som hela gruppen av isometrier av någon Riemann-yta.
- För släkte 2 maximeras ordningen av Bolza-ytan , med ordning 48.
- För släkte 3 maximeras ordningen av Klein quartic , med ordning 168; detta är den första Hurwitz-ytan, och dess automorfismgrupp är isomorf till den unika enkla gruppen av ordning 168, som är den näst minsta icke-abelska enkla gruppen. Denna grupp är isomorf till både PSL(2,7) och PSL(3,2) .
- För släkte 4 är Brings yta en mycket symmetrisk yta.
- För genus 7 maximeras ordningen av Macbeath-ytan , med ordning 504; detta är den andra Hurwitz-ytan, och dess automorfismgrupp är isomorf till PSL(2,8), den fjärde minsta icke-abelska enkla gruppen.

Funktionsteoretisk klassificering

Klassificeringsschemat ovan används vanligtvis av geometrar. Det finns en annan klassificering för Riemann-ytor som vanligtvis används av komplexa analytiker. Den använder en annan definition för "parabolisk" och "hyperbolisk". I detta alternativa klassificeringsschema kallas en Riemann-yta parabolisk om det inte finns några icke-konstanta negativa subharmoniska funktioner på ytan och kallas annars hyperbolisk . Denna klass av hyperboliska ytor är vidare uppdelad i underklasser beroende på om andra funktionsrum än de negativa subharmoniska funktionerna är degenererade, t.ex. Riemannytor på vilka alla gränsade holomorfa funktioner är konstanta, eller på vilka alla gränsade övertonsfunktioner är konstanta, eller på vilka alla positiva övertonsfunktioner är konstanta osv.

För att undvika förvirring, kalla klassificeringen baserad på mått för konstant krökning för den geometriska klassificeringen och den som baseras på degeneration av funktionsutrymmen för den funktionsteoretiska klassificeringen . Till exempel är Riemannytan som består av "alla komplexa tal utom 0 och 1" parabolisk i den funktionsteoretiska klassificeringen men den är hyperbolisk i den geometriska klassificeringen.

Se även

Satser om Riemann-ytor

Anteckningar

Farkas, Hershel M.; Kra, Irwin (1980), Riemann Surfaces (2:a upplagan), Berlin, New York: Springer-Verlag , ISBN 978-0-387-90465-8
Pablo Arés Gastesi, Riemann Surfaces Book .
Hartshorne, Robin (1977), Algebraic Geometry , Berlin, New York: Springer-Verlag , ISBN 978-0-387-90244-9 , MR 0463157 , OCLC 13348052 , esp. kapitel IV.
Jost, Jürgen (2006), Compact Riemann Surfaces , Berlin, New York: Springer-Verlag , s. 208–219, ISBN 978-3-540-33065-3
Papadopoulos, Athanase, red. (2007), Handbook of Teichmüller theory. Vol. I (PDF) , IRMA Lectures in Mathematics and Theoretical Physics, vol. 11, European Mathematical Society (EMS), Zürich, doi : 10.4171/029 , ISBN 978-3-03719-029-6 , MR 2284826 , S2CID 119593165
Lawton, Sean; Peterson, Elisha (2009), Papadopoulos, Athanase (red.), Handbook of Teichmüller theory. Vol. II , IRMA föreläsningar i matematik och teoretisk fysik, vol. 13, European Mathematical Society (EMS), Zürich, arXiv : math/0511271 , doi : 10.4171/055 , ISBN 978-3-03719-055-5 , MR 2524085 , S2CID 7268777726877
Papadopoulos, Athanase, red. (2012), Handbook of Teichmüller theory. Vol. III , IRMA Lectures in Mathematics and Theoretical Physics, vol. 19, European Mathematical Society (EMS), Zürich, doi : 10.4171/103 , ISBN 978-3-03719-103-3
* Remmert, Reinhold (1998). "Från Riemann-ytor till komplexa utrymmen". Seminarier och kongresser . Zbl 1044.01520 .
Siegel, Carl Ludwig (1955), "Meromorphe Funktionen auf kompakten analytischen Mannigfaltigkeiten", Nachrichten der Akademie der Wissenschaften i Göttingen. II. Mathematisch-Physikalische Klasse , 1955 : 71–77, ISSN 0065-5295 , MR 0074061
Weyl, Hermann (2009) [1913], The concept of a Riemann surface (3rd ed.), New York: Dover Publications , ISBN 978-0-486-47004-7 , MR 0069903

externa länkar

"Riemann yta" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
McMullen, C. "Komplex analys på Riemann Ytor Math 213b" (PDF) . Harvard Math . Harvard Universitet.

Myndighetskontroll
Nationalbibliotek	Spanien Frankrike BnF-data Tyskland Israel Förenta staterna Japan Tjeckien
Övrig	SNABB IdRef