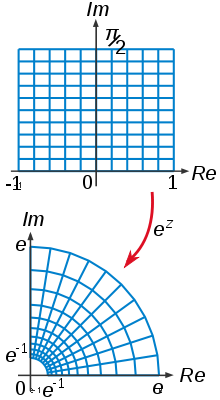
Biholomorfism

Den komplexa exponentialfunktionen avbildar biholomorft en rektangel till en kvartsring .

I den matematiska teorin om funktioner för en eller flera komplexa variabler , och även i komplex algebraisk geometri , är en biholomorfism eller biholomorf funktion en bijektiv holomorf funktion vars invers också är holomorf .

Formell definition

Formellt är en biholomorf funktion en funktion $\phi$ definierad på en öppen delmängd U av det $n$ -dimensionella komplexa utrymmet C ⁿ med värden i C ⁿ som är holomorft och en-till-en , så att dess bild är en öppen mängd $V$ i C ⁿ och inversen $\phi ^{-1}:V\to U$ är också holomorf . Mer generellt U och V vara komplexa grenrör . Liksom i fallet med funktioner av en enda komplex variabel, är ett tillräckligt villkor för att en holomorf karta ska vara biholomorf på sin bild att kartan är injektiv, i vilket fall den inversa också är holomorf (se Gunning 1990, Theorem I. 11).

Om det finns en biholomorfism ${\displaystyle \phi \colon U\to V} ,$ säger vi att U och V är biholomorft ekvivalenta eller att de är biholomorfa .

Riemanns kartläggningssats och generaliseringar

Om $n=1,$ varje enkelt ansluten öppen mängd förutom hela det komplexa planet biholomorft till enhetsskivan ( detta är Riemanns avbildningssats ). Situationen är mycket annorlunda i högre dimensioner. Till exempel är öppna enhetskulor och öppna enhetspolyskivor inte biholomorft ekvivalenta för $n>1.$ I själva verket finns det inte ens en riktig holomorf funktion från den ena till den andra.

Alternativa definitioner

I fallet med kartor f : U → C definierade på en öppen delmängd U av det komplexa planet C , definierar vissa författare (t.ex. Freitag 2009, definition IV.4.1) en konform karta som en injektiv karta med icke-nollderivata, dvs. f '( z )≠ 0 för varje z i U . Enligt denna definition är en karta f : U → C konform om och endast om f : U → f ( U ) är biholomorf. Andra författare (t.ex. Conway 1978) definierar en konform karta som en med en derivata som inte är noll, utan att kräva att kartan är injektiv. Enligt denna svagare definition av konformalitet behöver en konform karta inte vara biholomorf även om den är lokalt biholomorf. Till exempel, om f : U → U definieras av f ( z ) = z ² med U = C –{0}, så är f konform på U , eftersom dess derivata f '( z ) = 2 z ≠ 0, men det är inte biholomorft, eftersom det är 2-1.

•   Conway, John B. (1978). Funktioner för en komplex variabel . Springer-Verlag. ISBN 3-540-90328-3 .
•   D'Angelo, John P. (1993). Flera komplexa variabler och geometrin hos verkliga hyperytor . CRC Tryck. ISBN 0-8493-8272-6 .
•   Freitag, Eberhard; Busam, Rolf (2009). Komplex analys . Springer-Verlag. ISBN 978-3-540-93982-5 .
•   Gunning, Robert C. (1990). Introduktion till Holomorphic Functions of Several Variables, Vol. II . Wadsworth. ISBN 0-534-13309-6 .
•   Krantz, Steven G. (2002). Funktionsteori för flera komplexa variabler . American Mathematical Society. ISBN 0-8218-2724-3 .

Den här artikeln innehåller material från biholomorphically motsvarande på PlanetMath , som är licensierad under Creative Commons Attribution/Share-Alike-licensen .