Möbiusförvandling
Inom geometri och komplex analys är en Möbiustransformation av det komplexa planet en rationell funktion av formen
Geometriskt kan en Möbius-transformation erhållas genom att först utföra stereografisk projektion från planet till enhetens tvåsfär , rotera och flytta sfären till en ny plats och orientering i rymden, och sedan utföra stereografisk projektion (från sfärens nya position ) till planet. Dessa transformationer bevarar vinklar, mappar varje rak linje till en linje eller cirkel och mappar varje cirkel till en linje eller cirkel.
Möbiustransformationerna är de projektiva transformationerna av den komplexa projektiva linjen . De bildar en grupp som kallas Möbiusgruppen , som är den projektiva linjära gruppen PGL(2, C ). Tillsammans med sina undergrupper har den många tillämpningar inom matematik och fysik.
Möbiusförvandlingar är namngivna för att hedra August Ferdinand Möbius ; de är också olika namngivna homografier , homografiska omvandlingar , linjära bråkdelaromvandlingar , bilinjära omvandlingar , bråkdelar linjära omvandlingar och snurromvandlingar (i relativitetsteori).
Översikt
Möbiustransformationer definieras på det utökade komplexa planet dvs. komplext plan utökat med punkten i oändligheten ).
Stereografisk projektion identifierar med en sfär, som då kallas Riemann-sfären ; alternativt ses som den komplexa projektiva linjen . Möbius-transformationerna är exakt de bijektiva konforma kartorna från Riemann-sfären till sig själv, dvs. Riemanns-sfärens automorfism som en komplex mångfald ; alternativt är de automorfismerna av som en algebraisk variant. Därför bildar uppsättningen av alla Möbius-transformationer en grupp under sammansättning . Denna grupp kallas Möbius-gruppen och betecknas ibland .
Möbius-gruppen är isomorf mot gruppen av orienteringsbevarande isometrier av hyperboliskt 3-rum och spelar därför en viktig roll när man studerar hyperbolska 3-förgreningar .
Inom fysiken verkar identitetskomponenten i Lorentz-gruppen på den himmelska sfären på samma sätt som Möbius-gruppen verkar på Riemann-sfären . Faktum är att dessa två grupper är isomorfa. En observatör som accelererar till relativistiska hastigheter kommer att se mönstret av konstellationer som ses nära jorden kontinuerligt transformeras enligt infinitesimala Möbius-transformationer. Denna observation tas ofta som startpunkten för twistorteorin .
Vissa undergrupper av Möbius-gruppen bildar automorfismgrupperna för de andra enkelt sammankopplade Riemann-ytorna (det komplexa planet och det hyperboliska planet) . Som sådan spelar Möbius-transformationer en viktig roll i teorin om Riemann-ytor . Den grundläggande gruppen av varje Riemann-yta är en diskret undergrupp av Möbius-gruppen (se Fuchsian-gruppen och Kleinian-gruppen) . En särskilt viktig diskret undergrupp av Möbius-gruppen är den modulära gruppen ; det är centralt i teorin om många fraktaler , modulära former , elliptiska kurvor och Pelliska ekvationer .
Möbiustransformationer kan mer allmänt definieras i utrymmen med dimension n > 2 som de bijektiva konforma orienteringsbevarande kartorna från n -sfären till n -sfären. En sådan transformation är den mest allmänna formen av konform kartläggning av en domän. Enligt Liouvilles teorem kan en Möbius-transformation uttryckas som en sammansättning av översättningar, likheter , ortogonala transformationer och inversioner.
Definition
Den allmänna formen för en Möbius-transformation ges av
I fallet c ≠ 0 utvidgas denna definition till hela Riemanns sfär genom att definiera
Om c = 0 definierar vi
Sålunda är en Möbius-transformation alltid en bijektiv holomorf funktion från Riemann-sfären till Riemann-sfären.
Uppsättningen av alla Möbius-transformationer bildar en grupp under sammansättning . Denna grupp kan ges strukturen av ett komplext grenrör på ett sådant sätt att sammansättning och inversion är holomorfa kartor . Möbiusgruppen är då en komplex Lie-grupp . Möbiusgruppen betecknas vanligtvis eftersom den är automorfismgruppen i Riemann-sfären.
Fasta punkter
Varje icke-identitet Möbius-transformation har två fixpunkter på Riemann-sfären. Observera att de fasta punkterna räknas här med multiplicitet ; de paraboliska transformationerna är de där de fasta punkterna sammanfaller. Endera eller båda av dessa fasta punkter kan vara punkten i oändligheten.
Fastställande av fixpunkter
Förvandlingens fixpunkter
När c = 0 degenererar andragradsekvationen till en linjär ekvation och transformationen är linjär. Detta motsvarar situationen att en av de fasta punkterna är punkten i oändligheten. När a ≠ d är den andra fixpunkten ändlig och ges av
I det här fallet kommer transformationen att vara en enkel transformation som består av translationer , rotationer och dilatationer :
Om c = 0 och a = d är båda fixpunkterna i oändligheten, och Möbius-transformationen motsvarar en ren översättning:
Topologiska bevis
Topologiskt sett motsvarar det faktum att (icke-identitet) Möbius-transformationer fixar 2 punkter (med multiplicitet) att Euler-karakteristiken för sfären är 2:
är den projektiva linjära gruppen PGL(2, K ) skarpt 3-transitiv – för två ordnade trippel av distinkta punkter finns det en unik karta som tar den ena trippeln till den andra, precis som för Möbius-transformer, och med samma algebraiskt bevis (i huvudsak dimensionsräkning , eftersom gruppen är 3-dimensionell). Således är varje karta som fixar minst 3 punkter identiteten.
Därefter kan man se genom att identifiera Möbius-gruppen med att vilken Möbius-funktion som helst är homotop till identiteten. Faktum är att vilken medlem som helst av den allmänna linjära gruppen kan reduceras till identitetskartan genom eliminering av Gauss-Jordan, detta visar att den projektiva linjära gruppen också är vägbunden, vilket ger en homotopi till identitetskartan. Lefschetz –Hopf-satsen säger att summan av indexen (i detta sammanhang, multipliciteten) av de fasta punkterna på en karta med ändligt många fixpunkter är lika med kartans Lefschetz-tal , vilket i detta fall är spåret av identitetskartan på homologigrupper, vilket helt enkelt är Euler-karaktäristiken.
Däremot behöver den projektiva linjära gruppen för den verkliga projektiva linjen, PGL(2, R ) inte fixera några punkter – till exempel har inga (riktiga) fixpunkter: som en komplex transformation fixar den ± i – medan kartan 2 x fixar de två punkterna 0 och ∞. Detta motsvarar det faktum att Eulerkarakteristiken för cirkeln (verklig projektiv linje) är 0, och således säger Lefschetz fixpunktsats bara att den måste fixera minst 0 punkter, men möjligen fler.
Normal form
Möbiustransformationer skrivs också ibland i termer av deras fixpunkter i så kallad normalform . Vi behandlar först det icke-paraboliska fallet, för vilket det finns två distinkta fixpunkter.
Icke-paraboliskt fall :
Varje icke-parabolisk transformation är konjugerad till en dilatation/rotation, dvs en transformation av formen
Om f har distinkta fixpunkter ( γ 1 , γ 2 ) så har transformationen fixpunkter vid 0 och ∞ och är därför en dilatation: . Fixpunktsekvationen för transformationen f kan sedan skrivas
Att lösa f ger (i matrisform):
Från ovanstående uttryck kan man beräkna derivatorna av f vid de fasta punkterna:
Observera att, givet en ordning av de fasta punkterna, kan vi urskilja en av multiplikatorerna ( k ) för f som den karakteristiska konstanten för f . Att vända om ordningen på de fasta punkterna är ekvivalent med att ta den inversa multiplikatorn för den karakteristiska konstanten:
För loxodromic transformationer, när som helst | k | > 1, säger man att γ 1 är den repulsiva fixpunkten och γ 2 är den attraktiva fixpunkten. För | k | < 1, rollerna är omvända.
Paraboliskt fall :
I det paraboliska fallet finns det bara en fast punkt γ . Transformationen som skickar den punkten till ∞ är
Här kallas β för translationslängden . Fixpunktsformeln för en parabolisk transformation är då
Att lösa för f (i matrisform) ger
Observera att β inte är den karakteristiska konstanten för f , som alltid är 1 för en parabolisk transformation. Från ovanstående uttryck kan man räkna ut:
Förvandlingens poler
Punkten kallas polen för ; det är den punkten som transformeras till punkten i oändligheten under .
Den omvända polen är den punkt till vilken punkten i oändligheten transformeras. Punkten mitt emellan de två polerna är alltid densamma som punkten mitt emellan de två fasta punkterna:
Dessa fyra punkter är hörnen på ett parallellogram som ibland kallas det karakteristiska parallellogrammet för transformationen.
En transformation kan specificeras med två fixpunkter γ 1 , γ 2 och polen .
Detta tillåter oss att härleda en formel för konvertering mellan k och givet :
Det sista uttrycket sammanfaller med ett av de (ömsesidigt reciproka) egenvärdesförhållandena i matrisen
Enkla Möbiustransformationer och komposition
En Möbiustransformation kan vara sammansatt som en sekvens av enkla transformationer.
Följande enkla transformationer är också Möbius-transformationer:
- är en översättning .
- är en kombination av en homoteti och en rotation . Om så är det en rotation, om så är det en homoteti.
- ( inversion och reflektion med avseende på den reella axeln)
Sammansättning av enkla transformationer
Om , låt:
- ( översättning av d / c )
- ( inversion och reflektion med avseende på den reella axeln)
- ( homoteti och rotation )
- (översättning med a / c )
Sedan kan dessa funktioner komponeras , vilket visar att, if
Denna nedbrytning gör många egenskaper hos Möbius-transformationen uppenbara.
Elementära egenskaper
En Möbius-transformation är ekvivalent med en sekvens av enklare transformationer. Sammansättningen gör många egenskaper hos Möbius-transformationen uppenbara.
Formel för den omvända transformationen
Existensen av den inversa Möbius-transformationen och dess explicita formel härleds lätt genom sammansättningen av de inversa funktionerna i de enklare transformationerna. Det fi vill gi säga definiera funktioner g 1 , g 2 , g 3 , g 4 så att varje är inversen av . Sedan kompositionen
Bevarande av vinklar och generaliserade cirklar
Från denna nedbrytning ser vi att Möbius-transformationer bär över alla icke-triviala egenskaper hos cirkelinversion . Till exempel reduceras bevarandet av vinklar till att bevisa att cirkelinversion bevarar vinklar eftersom de andra typerna av transformationer är dilatationer och isometrier (translation, reflektion, rotation), som trivialt bevarar vinklar.
Dessutom kartlägger Möbius-transformationer generaliserade cirklar till generaliserade cirklar eftersom cirkelinversion har denna egenskap. En generaliserad cirkel är antingen en cirkel eller en linje, varvid den senare betraktas som en cirkel genom punkten i oändligheten. Observera att en Möbius-transformation inte nödvändigtvis mappar cirklar till cirklar och linjer till linjer: den kan blanda de två. Även om den mappar en cirkel till en annan cirkel, mappar den inte nödvändigtvis den första cirkelns centrum till den andra cirkelns centrum.
Korsförhållande bevarande
Korsförhållanden är invarianta under Möbius-transformationer. Det vill säga om en Möbius-transformation mappar fyra distinkta punkter till fyra distinkta punkter respektive, sedan
Om en av punkterna är punkten i oändligheten, då är korsförhållandet måste definieras genom att ta lämplig gräns; t.ex. är korsförhållandet för
Korsförhållandet för fyra olika punkter är verkligt om och endast om det finns en linje eller en cirkel som passerar genom dem. Detta är ytterligare ett sätt att visa att Möbiustransformationer bevarar generaliserade cirklar.
Konjugation
Två punkter z 1 och z 2 är konjugerade med avseende på en generaliserad cirkel C , om, givet en generaliserad cirkel D som går genom z 1 och z 2 och skär C i två punkter a och b , ( z 1 , z 2 ; a , b ) är i harmoniskt korsförhållande (dvs deras korsförhållande är −1). Denna egenskap beror inte på valet av cirkeln D . Denna egenskap kallas också ibland för att vara symmetrisk med avseende på en linje eller cirkel.
Två punkter z , z ∗ är konjugerade med avseende på en linje, om de är symmetriska med avseende på linjen. Två punkter konjugeras med avseende på en cirkel om de byts ut genom inversionen med avseende på denna cirkel.
0 Punkten z ∗ konjugerar till z när L är linjen som bestäms av vektorn baserad e iθ i punkten z kan uttryckligen ges som
0 Punkten z ∗ konjugerar till z när C är cirkeln med radien r centrerad z kan uttryckligen ges som
Eftersom Möbius-transformationer bevarar generaliserade cirklar och korsförhållanden, bevarar de också konjugationen.
Projektiva matrisrepresentationer
Den naturliga verkan av PGL(2, C ) på den komplexa projektiva linjen CP 1 är exakt den naturliga verkan av Möbius-gruppen på Riemann-sfären, där den projektiva linjen CP 1 och Riemanns-sfären identifieras enligt följande:
Här är [ z 1 : z 2 ] homogena koordinater på CP 1 ; punkten [1:0] motsvarar punkten ∞ i Riemann-sfären. Genom att använda homogena koordinater kan många beräkningar som involverar Möbius-transformationer förenklas, eftersom inga fallskillnader som handlar om ∞ krävs.
Varje inverterbar komplex 2×2-matris
Eftersom matrisen ovan är inverterbar om och endast om dess determinant ad − bc inte är noll, inducerar detta en identifiering av verkan av gruppen av Möbius-transformationer med verkan av PGL(2, C ) på den komplexa projektiva linjen. I denna identifiering motsvarar ovanstående matris Möbius-transformationen
Denna identifiering är en gruppisomorfism , eftersom multiplikationen av med en skalär som inte är noll inte ändrar elementet i PGL(2, C ), och, eftersom denna multiplikation består av att multiplicera alla matrisposter med ändrar detta inte motsvarande Möbius-transformation.
För vilket fält som helst kan man på liknande sätt identifiera gruppen PGL(2, K ) för de projektiva linjära automorfismerna med gruppen av fraktionerade linjära transformationer. Detta används flitigt; till exempel i studiet av homografier av den verkliga linjen och dess tillämpningar inom optik .
Om man dividerar med kvadratroten av dess determinant, får man en matris med determinant ett. Detta inducerar en surjektiv grupphomomorfism från den speciella linjära gruppen SL(2, C ) till PGL(2, C ), med som kärna.
Detta gör det möjligt att visa att Möbius-gruppen är en 3-dimensionell komplex Lie-grupp (eller en 6-dimensionell verklig Lie-grupp), som är en halvenkel och icke- kompakt , och att SL(2, C ) är en dubbel täckning av PSL( 2, C ). Eftersom SL(2, C ) är enkelt ansluten är det det universella täcket för Möbius-gruppen, och den grundläggande gruppen för Möbius-gruppen är Z 2 .
Ange en transformation med tre punkter
Givet en uppsättning av tre distinkta punkter på Riemann-sfären och en andra uppsättning distinkta punkter , det finns exakt en Möbius-transformation med för . (Med andra ord: Möbiusgruppens verkan på Riemann-sfären är skarpt 3-transitiv .) Det finns flera sätt att bestämma från de givna uppsättningarna av punkter.
Mappa först till 0, 1, ∞
Det är lätt att kontrollera att Möbiusförvandlingen
med matris
mappar till respektive. Om en av är , då erhålls den korrekta formeln för från ovanstående en genom att först dividera alla poster med och sedan ta gränsen .
Om definieras på liknande sätt för att mappa till sedan matrisen som mappar till blir
Stabilisatorn för (som en oordnad mängd) är en undergrupp känd som den anharmoniska gruppen .
Explicit determinantformel
Ekvationen
är ekvivalent med ekvationen för en standardhyperbol
i -planet. Problemet med att konstruera en Möbius-transformation som avbildar en trippel till en annan trippel är alltså ekvivalent med att hitta koefficienterna av hyperbeln som passerar genom punkterna . En explicit ekvation kan hittas genom att utvärdera determinanten
med hjälp av en Laplace-expansion längs första raden. Detta resulterar i determinantformlerna
för koefficienterna för den representerande matrisen . Den konstruerade matrisen har determinant lika med som inte försvinner om resp. är parvis olika, så Möbius-transformationen är väldefinierad. Om en av punkterna eller är , så dividerar vi först alla fyra determinanterna med denna variabel och tar sedan gränsen när variabeln närmar sig .
Undergrupper av Möbiusgruppen
Om vi kräver att koefficienterna för en Möbius-transformation ska vara reella tal med , vi erhålla en undergrupp av Möbius-gruppen betecknad som PSL(2, R ) . Detta är gruppen av de Möbius-transformationer som kartlägger det övre halvplanet H = x + i y : y > 0 till sig själv, och är lika med gruppen av alla biholomorfa (eller motsvarande: bijektiva , konforma och orienteringsbevarande) kartor H → H. _ Om en korrekt metrik införs blir det övre halvplanet en modell av hyperbolplanet H 2 , Poincarés halvplansmodell och PSL(2, R ) är gruppen av alla orienteringsbevarande isometrier av H 2 i denna modell.
Undergruppen av alla Möbius-transformationer som mappar den öppna disken D = z : | z | < 1 till sig själv består av alla transformationer av formen
Eftersom båda ovanstående undergrupper fungerar som isometrigrupper av H 2 är de isomorfa. En konkret isomorfism ges genom konjugering med transformationen
Alternativt kan du överväga en öppen skiva med radien r , centrerad vid r i . Poincaré-skivmodellen i denna skiva blir identisk med den övre halvplansmodellen när r närmar sig ∞.
En maximal kompakt undergrupp av Möbiusgruppen ges av ( Tóth 2002 )
Ikosaedriska grupper av Möbius-transformationer användes av Felix Klein för att ge en analytisk lösning på den kvintiska ekvationen i ( Klein 1888) ; en modern utläggning ges i ( Tóth 2002 ).
Om vi kräver att koefficienterna a , b , c , d för en Möbius-transformation ska vara heltal med ad − bc = 1, får vi den modulära gruppen PSL(2, Z ), en diskret undergrupp av PSL(2, R ) som är viktig i studiet av gitter i det komplexa planet, elliptiska funktioner och elliptiska kurvor . De diskreta undergrupperna av PSL(2, R ) är kända som fuchsiska grupper ; de är viktiga i studiet av Riemann-ytor .
Klassificering

I följande diskussion kommer vi alltid att anta att den representerande matrisen är normaliserad så att .
Non-identitet Möbius-transformationer klassificeras vanligen i fyra typer, paraboliska , elliptiska , hyperboliska och loxodromiska , med de hyperboliska som är en underklass av de loxodromiska. Klassificeringen har både algebraisk och geometrisk betydelse. Geometriskt resulterar de olika typerna i olika transformationer av det komplexa planet, vilket figurerna nedan illustrerar.
De fyra typerna kan särskiljas genom att titta på spåret tr . Observera att spåret är invariant under konjugering , det vill säga
Paraboliska transformationer
En icke-identitet Möbius-transformation definierad av en matris av determinant ett sägs vara parabolisk om
Mängden av alla paraboliska Möbiustransformationer med en given fixpunkt i bildar tillsammans med identiteten en undergrupp isomorf till gruppen av matriser
Karakteristisk konstant
Alla icke-paraboliska transformationer har två fasta punkter och definieras av en matriskonjugat till
Elliptiska transformationer

Transformationen sägs vara elliptisk om den kan representeras av en matris vars spår är verkligt med
En transform är elliptisk om och endast om | λ | = 1 och λ ≠ ±1. Om man skriver , är en elliptisk transform konjugerad till
Observera att för alla med karakteristisk konstant k , är den karakteristiska konstanten för k n . Således är alla Möbius-transformationer av ändlig ordning elliptiska transformationer, nämligen exakt de där λ är en rot av enhet , eller, ekvivalent, där α är en rationell multipel av π . Den enklaste möjligheten för en bråkdelsmultipel betyder α = π /2, vilket också är det unika fallet för betecknas också som en cirkulär transformera ; detta motsvarar geometriskt rotation med 180° omkring två fixpunkter. Denna klass representeras i matrisform som:
Hyperboliska transformationer
Transformen sägs vara hyperbolisk om den kan representeras av en matris vars spår är verkligt med
En transformation är hyperbolisk om och endast om λ är reell och λ ≠ ±1.
Loxodromic transformationer
Transformen sägs vara loxodromic om inte är i [0,4]. En transformation är loxodromic om och endast om .
Historiskt sett hänvisar navigering med loxodrome eller rhumb line till en bana av konstant bäring ; den resulterande banan är en logaritmisk spiral , som till formen liknar transformationerna av det komplexa planet som en loxodromic Möbius-transformation gör. Se de geometriska figurerna nedan.
Allmänna klassificeringen
| Omvandling | Spår i kvadrat | Multiplikatorer | Klassrepresentant | |
|---|---|---|---|---|
| Cirkulär | σ = 0 | k = −1 | z ↦ − z | |
| Elliptisk | 0 ≤ σ < 4 | | k | = 1 | z ↦ e i θ z | |
| Parabolisk | σ = 4 | k = 1 | z ↦ z + a | |
| Hyperbolisk | 4 < σ < ∞ | z ↦ e θ z | ||
| Loxodromic | σ ∈ C \ [0,4] | z ↦ kz | ||
Det verkliga fallet och en anteckning om terminologi
Över de reella siffrorna (om koefficienterna måste vara reella) finns det inga icke-hyperboliska loxodromic transformationer, och klassificeringen är i elliptiska, paraboliska och hyperboliska, som för verkliga koner . Terminologin beror på att man betraktar halva det absoluta värdet av spåret, |tr|/2, eftersom excentriciteten i transformationen – division med 2 korrigerar för dimensionen, så identiteten har excentricitet 1 (tr/ n används ibland som en alternativ för spåret av denna anledning), och det absoluta värdet korrigerar för att spåret endast definieras upp till en faktor på ±1 på grund av arbete i PSL. Alternativt kan man använda halva kurvan i kvadrat som en proxy för excentriciteten i kvadrat, som gjordes ovan; dessa klassificeringar (men inte de exakta excentricitetsvärdena, eftersom kvadrat- och absolutvärden är olika) överensstämmer för verkliga spår men inte komplexa spår. Samma terminologi används för klassificeringen av element i SL(2, R ) (det 2-faldiga omslaget), och analoga klassificeringar används på andra ställen. Loxodromic transformationer är ett väsentligen komplext fenomen och motsvarar komplexa excentriciteter.
Geometrisk tolkning av den karakteristiska konstanten
Följande bild visar (efter stereografisk transformation från sfären till planet) de två fixpunkterna i en Möbius-transformation i det icke-paraboliska fallet:
Den karakteristiska konstanten kan uttryckas i termer av dess logaritm :
Elliptiska transformationer
Om ρ = 0, så är de fasta punkterna varken attraktiva eller frånstötande utan likgiltiga, och omvandlingen sägs vara elliptisk . Dessa transformationer tenderar att flytta alla punkter i cirklar runt de två fixpunkterna. Om en av de fasta punkterna är i oändlighet, motsvarar detta att göra en affin rotation runt en punkt.
Om vi tar undergruppen med en parameter som genereras av valfri elliptisk Möbius-transformation, får vi en kontinuerlig transformation, så att varje transformation i undergruppen fixar samma två punkter. Alla andra punkter flyter längs en familj av cirklar som är kapslade mellan de två fasta punkterna på Riemann-sfären. I allmänhet kan de två fasta punkterna vara vilka som helst två distinkta punkter.
Detta har en viktig fysisk tolkning. Föreställ dig att någon observatör roterar med konstant vinkelhastighet kring någon axel. Då kan vi ta de två fasta punkterna för att vara himmelsfärens nord- och sydpoler. Natthimlens utseende omvandlas nu kontinuerligt på exakt det sätt som beskrivs av den enparameters undergruppen av elliptiska transformationer som delar de fixerade punkterna 0, ∞ och med talet α som motsvarar den konstanta vinkelhastigheten för vår observatör.
Här är några figurer som illustrerar effekten av en elliptisk Möbius-transformation på Riemann-sfären (efter stereografisk projektion till planet):
Dessa bilder illustrerar effekten av en enda Möbius-transformation. Den enparameters undergrupp som den genererar kontinuerligt punkter längs familjen av cirkelbågar som föreslagits av bilderna.
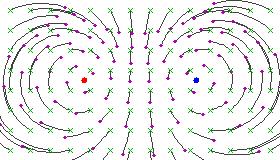
Hyperboliska transformationer
Om α är noll (eller en multipel av 2 π ), så sägs transformationen vara hyperbolisk . Dessa transformationer tenderar att flytta punkter längs cirkulära banor från en fast punkt till den andra.
Om vi tar undergruppen med en parameter som genereras av någon hyperbolisk Möbius-transformation, får vi en kontinuerlig transformation, så att varje transformation i undergruppen fixar samma två punkter. Alla andra punkter flyter längs en viss familj av cirkelbågar bort från den första fasta punkten och mot den andra fixpunkten. I allmänhet kan de två fasta punkterna vara vilka som helst två distinkta punkter på Riemann-sfären.
Även detta har en viktig fysisk tolkning. Föreställ dig att en observatör accelererar (med konstant accelerationsstorlek) i riktning mot nordpolen på sin himmelssfär. Sedan omvandlas natthimlens utseende på exakt det sätt som beskrivs av den enparameters undergruppen av hyperboliska transformationer som delar de fasta punkterna 0, ∞, med det reella talet ρ som motsvarar storleken på hans accelerationsvektor. Stjärnorna verkar röra sig längs longituder, bort från sydpolen mot nordpolen. (Längdgraderna visas som cirkulära bågar under stereografisk projektion från sfären till planet.)
Här är några figurer som illustrerar effekten av en hyperbolisk Möbius-transformation på Riemann-sfären (efter stereografisk projektion till planet):
Dessa bilder liknar fältlinjerna för en positiv och en negativ elektrisk laddning belägna vid de fasta punkterna, eftersom de cirkulära flödeslinjerna bildar en konstant vinkel mellan de två fasta punkterna.
Loxodromic transformationer
Om både ρ och α är icke-noll, sägs transformationen vara loxodromic . Dessa transformationer tenderar att flytta alla punkter i S-formade banor från en fast punkt till en annan.
Ordet " loxodrome " kommer från grekiskan: "λοξος (loxos), lutande + δρόμος (dromos), kurs ". När man seglar på konstant bäring – om man håller en kurs på (säg) nordost kommer man så småningom att sluta segla runt nordpolen i en logaritmisk spiral . På mercatorprojektionen är en sådan kurs en rak linje, eftersom nord- och sydpolen skjuter ut i det oändliga. Vinkeln som loxodromen understryker i förhållande till longitudlinjerna (dvs. dess lutning, spiralens "täthet") är argumentet för k . Givetvis kan Möbiustransformationer ha sina två fixpunkter var som helst, inte bara vid nord- och sydpolen. Men varje loxodromic transformation kommer att konjugeras till en transformation som flyttar alla punkter längs sådana loxodromer.
Om vi tar en-parameter-undergruppen som genereras av någon loxodromic Möbius-transformation, får vi en kontinuerlig transformation, så att varje transformation i undergruppen fixar samma två punkter. Alla andra punkter flyter längs en viss familj av kurvor, bort från den första fasta punkten och mot den andra fixpunkten. Till skillnad från det hyperboliska fallet är dessa kurvor inte cirkelbågar, utan vissa kurvor som under stereografisk projektion från sfären till planet framstår som spiralkurvor som vrider sig moturs oändligt ofta runt en fast punkt och vrider sig medurs oändligt ofta runt den andra fixpunkten. I allmänhet kan de två fasta punkterna vara vilka som helst två distinkta punkter på Riemann-sfären.
Du kan förmodligen gissa den fysiska tolkningen i fallet när de två fixpunkterna är 0, ∞: en observatör som både roterar (med konstant vinkelhastighet) kring en axel och rör sig längs samma axel, kommer att se natthimlens utseende transformera enligt enparameters undergruppen av loxodromiska transformationer med fixpunkter 0, ∞ och med ρ, α bestämt av storleken på den faktiska linjära och vinkelhastigheten.
Stereografisk projektion
Dessa bilder visar Möbius-transformationer stereografiskt projicerade på Riemann-sfären . Observera särskilt att när det projiceras på en sfär, ser specialfallet av en fast punkt i oändligheten inte annorlunda ut från att ha de fasta punkterna på en godtycklig plats.
| En fast punkt i oändligheten | ||
| Fasta punkter diametralt motsatta | ||
| Fasta punkter på en godtycklig plats | ||
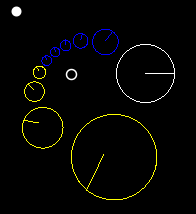
Itererar en förvandling
Om en transformation har fixpunkter γ 1 , γ 2 och karakteristisk konstant k , då kommer att ha .
Detta kan användas för att iterera en transformation, eller för att animera en genom att dela upp den i steg.
Dessa bilder visar tre punkter (röd, blå och svart) som kontinuerligt itereras under transformationer med olika karakteristiska konstanter.
 |
 |
 |
|
Och dessa bilder visar vad som händer när du transformerar en cirkel under hyperboliska, elliptiska och loxodromiska transformationer. Observera att i de elliptiska och loxodromic bilderna är α-värdet 1/10.
Högre dimensioner
I högre dimensioner är en Möbius-transformation en homeomorfism av enpunktskomprimeringen av R , som är en finit sammansättning av inversioner i sfärer och reflektioner i hyperplan . Liouvilles teorem i konformal geometri säger att i dimension minst tre är alla konforma transformationer Möbiustransformationer. Varje Möbius-transformation kan sättas i form
där , , är en ortogonal matris , och är 0 eller 2. Gruppen Möbiustransformationer kallas även Möbiusgruppen .
De orienteringsbevarande Möbiustransformationerna utgör den sammanhängande komponenten av identiteten i Möbiusgruppen. I dimension n = 2 är de orienteringsbevarande Möbius-transformationerna exakt de kartor över Riemann-sfären som täcks här. De orienteringsomvändande erhålls från dessa genom komplex konjugering.
Domänen för Möbius-transformationer, dvs , är homeomorf till den n -dimensionella sfären . Den kanoniska isomorfismen mellan dessa två utrymmen är Cayley-transformen , som i sig är en Möbius-transformation av . Denna identifiering innebär att Möbius-transformationer också kan ses som konforma isomorfismer av . n - sfären , tillsammans med Möbius-gruppens verkan, är en geometrisk struktur (i betydelsen av Kleins Erlangen-program) som kallas Möbius geometri .
Ansökningar
Lorentz förvandling
En isomorfism av Möbius-gruppen med Lorentz-gruppen noterades av flera författare: Baserat på tidigare arbete av Felix Klein (1893, 1897) om automorfa funktioner relaterade till hyperbolisk geometri och Möbius-geometri, visade Gustav Herglotz (1909) att hyperboliska rörelser (dvs. isometriska automorfismer av ett hyperboliskt utrymme ) som omvandlar enhetssfären till sig själv motsvarar Lorentz-transformationer, genom vilka Herglotz kunde klassificera Lorentz-transformationerna med en parameter i loxodromic, elliptiska, hyperboliska och paraboliska grupper. Andra författare inkluderar Emil Artin (1957), HSM Coxeter (1965) och Roger Penrose , Wolfgang Rindler (1984), Tristan Needham (1997) och WM Olivia (2002).
0 Minkowskirymden består av det fyrdimensionella reella koordinatutrymmet R 4 bestående av rymden av ordnade fyrdubblar ( x , x 1 , x 2 , x 3 ) av reella tal, tillsammans med en kvadratisk form
null cone Med lån av terminologi från speciell relativitet anses punkter med Q > 0 vara tidsliknande ; dessutom, om 0 x > 0 , så kallas punkten framtidspekande . Punkter med Q < 0 kallas spacelike . Nollkonen S består av de punkter där Q = 0 = future null cone N+ are those points on the null cone with x0 > 0. The celestial sphere is then identified with the collection of rays in N+ whose initial point is the origin of R4. The collection of linear transformations on R4 with positive determinant preserving the quadratic form Q and preserving the time direction form the restricted Lorentz group SO+(1,3).
I samband med himmelssfärens geometri identifieras gruppen av transformationer SO + (1,3) med gruppen PSL(2, C ) av Möbius-transformationer av sfären. Till varje 0 ( x , x 1 , x 2 , x 3 ) ∈ R 4 , associera den hermitiska matrisen
Determinanten för matrisen X är lika med 0 Q ( x , x , x 2 , x 3 ) . 1 Den speciella linjära gruppen verkar på utrymmet för sådana matriser via
-
()
för varje A ∈ SL(2, C ), och denna åtgärd av SL(2, C ) bevarar determinanten för X eftersom det A = 1 . Eftersom determinanten för X identifieras med den kvadratiska formen Q , verkar SL(2, C ) genom Lorentz-transformationer. På dimensionella grunder täcker SL(2, C ) ett område av identiteten för SO(1,3). Eftersom SL(2, C ) är ansluten täcker den hela den begränsade Lorentz-gruppen SO + (1,3). Dessutom, eftersom kärnan i åtgärden ( 1 ) är undergruppen {± I }, ger övergång till kvotgruppen gruppen isomorfism
-
()
0 Fokusera nu på fallet när ( x , x 1 , x 2 , x 3 ) är noll, matrisen X har noll determinant och delar sig därför som den yttre produkten av en komplex tvåvektor ξ med dess komplexa konjugat:
-
()
Tvåkomponentvektorn ξ påverkas av SL(2, C ) på ett sätt som är kompatibelt med ( 1 ). Det är nu klart att kärnan i representationen av SL(2, C ) på hermitiska matriser är {± I }.
0 Verkan av PSL(2, C ) på den himmelska sfären kan också beskrivas geometriskt med hjälp av stereografisk projektion . Betrakta först hyperplanet i R 4 givet av x = 1. Himmelssfären kan identifieras med sfären S + för skärningen av hyperplanet med den framtida nollkonen N + . Den stereografiska projektionen från nordpolen (1,0,0,1) av denna sfär till planet x 3 = 0 tar en punkt med koordinater (1, x 1 , x 2 , x 3 ) med
Introduktion av den komplexa koordinaten
-
()
Verkan av SO + (1,3) på punkterna i N + bevarar inte hyperplanet S + , men att agera på punkter i S + och sedan skala om så att resultatet återigen är i S + ger en handling av SO + ( 1,3) på sfären som går över till en åtgärd på den komplexa variabeln ζ. I själva verket är denna verkan genom fraktionerad linjär transformation, även om detta inte är lätt att se från denna representation av himmelssfären. Omvänt, för varje fraktionerad linjär transformation av ζ går variabeln över till en unik Lorentz-transformation på N + , möjligen efter en lämplig (unikt bestämd) omskalning.
En mer oföränderlig beskrivning av den stereografiska projektionen som gör att handlingen kan ses tydligare är att betrakta variabeln ζ = z : w som ett förhållande mellan ett par homogena koordinater för den komplexa projektiva linjen CP 1 . Den stereografiska projektionen går över till en transformation från C 2 − {0} till N + som är homogen av grad två med avseende på verkliga skalningar
-
()
som överensstämmer med ( 4 ) vid begränsning till skalor där Komponenterna i ( 5 ) är just de som erhålls från den yttre produkten
Sammanfattningsvis överensstämmer agerandet från den begränsade Lorentz-gruppen SO + (1,3) med Möbius-gruppens PSL(2, C ). Detta motiverar följande definition. I dimension n ≥ 2 är Möbiusgruppen Möb( n ) gruppen av alla orienteringsbevarande konforma isometrier av den runda sfären S n till sig själv. Genom att realisera den konforma sfären som utrymmet för framtidspekande strålar av nollkonen i Minkowski-rymden R 1,n+1 , finns det en isomorfism av Möb( n ) med den begränsade Lorentz-gruppen SO + (1, n +1 ) ) av Lorentz-transformationer med positiv determinant, som bevarar tidens riktning.
Coxeter började istället med den ekvivalenta kvadratiska formen
Han identifierade Lorentz-gruppen med transformationer för vilka { x : Q( x ) = -1} är stabil . Sedan tolkade han x:en som homogena koordinater och { x : Q( x ) = 0}, nollkonen , som Cayleys absoluta för ett hyperboliskt utrymme av punkter { x : Q( x ) < 0}. Därefter introducerade Coxeter variablerna
så att den Lorentz-invarianta kvadriken motsvarar sfären Coxeter noterar att Felix Klein också skrev om denna korrespondens och tillämpade stereografisk projektion från (0, 0, 1) till det komplexa planet Coxeter använde det faktum att cirklar i det inversiva planet representerar plan av hyperboliskt rymd, och den allmänna homografin är produkten av inversioner i två eller fyra cirklar, motsvarande den allmänna hyperboliska förskjutningen som är produkten av inversioner i två eller fyra plan.
Hyperboliskt utrymme
Som sett ovan verkar Möbius-gruppen PSL(2, C ) på Minkowski-rummet som gruppen av de isometrier som bevarar ursprunget, rummets orientering och tidens riktning. Om vi begränsar oss till de punkter där Q =1 i den positiva ljuskonen, som bildar en modell av hyperboliskt 3-rums H 3 , ser vi att Möbius-gruppen verkar på H 3 som en grupp av orienteringsbevarande isometrier. Faktum är att Möbius-gruppen är lika med gruppen av orienteringsbevarande isometrier av hyperboliskt 3-rum.
Om vi använder Poincaré-bollmodellen , som identifierar enhetsbollen i R 3 med H 3 , så kan vi tänka på Riemann-sfären som den "konforma gränsen" för H 3 . Varje orienteringsbevarande isometri av H 3 ger upphov till en Möbius-transformation på Riemann-sfären och vice versa; detta är den allra första observationen som leder till AdS/CFT-korrespondensförmodan i fysik.
Se även
- Bilinjär transformation
- Konform geometri
- Fuchsisk grupp
- Generaliserad cirkel
- Hyperbolisk geometri
- Oändliga sammansättningar av analytiska funktioner
- Inversionstransformation
- Kleinian grupp
- Lie sfärens geometri
- Linjär fraktionell transformation
- Liouvilles sats (konforma avbildningar)
- Lorentz grupp
- Modulär grupp
- Poincaré halvplansmodell
- Projektiv geometri
- Projektiv linje över en ring
- Lorentz-gruppens representationsteori
- Schottky-gruppen
Anteckningar
Specifik
Allmän
- Arnold, Douglas N.; Rogness, Jonathan (2008), "Möbius Transformations Revealed" (PDF) , Notices of the AMS , 55 (10): 1226–1231
- Beardon, Alan F. (1995), The Geometry of Discrete Groups , New York: Springer-Verlag, ISBN 978-0-387-90788-8
- Hall, GS (2004), Symmetries and Curvature Structure in General Relativity , Singapore: World Scientific, ISBN 978-981-02-1051-9 (Se kapitel 6 för klassificeringen, upp till konjugacy, av Lie-subalgebrerna i Lie-algebra från Lorentz-gruppen.)
- Katok, Svetlana (1992), Fuchsian Groups , Chicago: University of Chicago Press, ISBN 978-0-226-42583-2 Se kapitel 2 .
- Klein, Felix (1888), Föreläsningar om ikosaedern och lösningen av ekvationer av femte graden (Dover red.), ISBN 978-0-486-49528-6 .
- Knopp, Konrad (1952), Elements of the Theory of Functions , New York: Dover, ISBN 978-0-486-60154-0 (Se kapitel 3–5 i denna klassiska bok för en vacker introduktion till Riemann-sfären, stereografisk projektion , och Möbius-transformationer.)
- Mumford, David ; Serie, Caroline; Wright, David (2002), Indra's Pearls: The Vision of Felix Klein , Cambridge University Press, ISBN 978-0-521-35253-6 (Riktar till icke-matematiker, ger en utmärkt presentation av teori och resultat, rikt illustrerad med diagram .)
- Needham, Tristan (1997), Visual Complex Analysis , Oxford: Clarendon Press, ISBN 978-0-19-853446-4 (Se kapitel 3 för en vackert illustrerad introduktion till Möbius-transformationer, inklusive deras klassificering upp till konjugation.)
- Penrose, Roger ; Rindler, Wolfgang (1984), Spinors and space-time, Volym 1: Two-spinor calculus and relativistic fields , Cambridge University Press, ISBN 978-0-521-24527-2
- Schwerdtfeger, Hans (1979), Geometry of Complex Numbers , Dover, ISBN 978-0-486-63830-0 (Se kapitel 2 för en introduktion till Möbius-transformationer.)
- Tóth, Gábor (2002), Finita Möbius-grupper, minimala nedsänkningar av sfärer och moduler
Vidare läsning
- Lawson, MV (1998). "The Möbius Inverse Monoid" . Journal of Algebra . 200 (2): 428. doi : 10.1006/jabr.1997.7242 .





































































![{\displaystyle [z_{1}:z_{2}]\ \thicksim {\frac {z_{1}}{z_{2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b4893a9352becf62e6802c31e40598ca194503f)
![{\displaystyle [z_{1}:z_{1}]\mapsto [w_{1}:w_{2}],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9363b0ec9936944c7f32a272f0e035d0446c5a2)