Riktigt projektivt plan

Grundpolygonen i det projektiva planet .	Möbiusremsan med en enda kant, kan förslutas till ett projektivt plan genom att limma ihop motsatta öppna kanter .	Som jämförelse är Klein-flaskan en Möbius-remsa försluten till en cylinder.

Inom matematiken är det verkliga projektiva planet ett exempel på ett kompakt icke- orienterbart tvådimensionellt grenrör ; med andra ord en ensidig yta . Det kan inte bäddas in i standard tredimensionellt utrymme utan att skära sig själv. Den har grundläggande tillämpningar för geometri , eftersom den vanliga konstruktionen av det verkliga projektiva planet är som utrymmet av linjer i $\mathbb {R} ^{3}$ som passerar genom origo.

Planet beskrivs också ofta topologiskt, i termer av en konstruktion baserad på Möbiusremsan : om man kunde limma Möbiusremsan (enda) kanten på sig själv i rätt riktning, skulle man få det projektiva planet . (Detta kan inte göras i tredimensionellt utrymme utan att ytan skär sig själv.) På motsvarande sätt ger limning av en skiva längs Möbiusremsans gräns det projektiva planet. Topologiskt har den Euler-karaktäristik 1, därav ett demigenus (icke-orienterbart släkte, Euler-släkte) på 1.

Eftersom Möbiusremsan i sin tur kan konstrueras av en kvadrat genom att limma ihop två av dess sidor med en halvvridning, kan det verkliga projektiva planet således representeras som en enhetskvadrat (det vill säga $[0, 1] \times [ 0,1]$ ) med sina sidor identifierade av följande ekvivalensrelationer :

(0, y) ~ (1, 1 - y)

för

0 \leq y \leq 1

och

(x, 0) ~ (1 - x, 1)

för

0 \leq x \leq 1,

som i diagrammet längst till vänster som visas här.

Exempel

Projektiv geometri handlar inte nödvändigtvis om krökning och det verkliga projektiva planet kan vridas upp och placeras i det euklidiska planet eller 3-rummet på många olika sätt. Några av de viktigare exemplen beskrivs nedan.

Det projektiva planet kan inte bäddas in (det vill säga utan skärningspunkt) i det tredimensionella euklidiska rummet . Beviset för att det projektiva planet inte bäddas in i det tredimensionella euklidiska rymden går så här: Om man antar att det bäddar in, skulle det begränsa ett kompakt område i det tredimensionella euklidiska rummet av den generaliserade Jordan-kurvans teorem . Den utåtriktade enhetens normala vektorfält skulle då ge en orientering av gränsgrenröret, men gränsgrenröret skulle vara det projektiva planet , som inte är orienterbart. Detta är en motsägelse, och därför måste vårt antagande att det bäddas in ha varit falskt.

Den projektiva sfären

Betrakta en sfär och låt sfärens stora cirklar vara "linjer", och låt par av antipodalpunkter vara "punkter". Det är lätt att kontrollera att detta system följer de axiom som krävs för ett projektivt plan :

vilket par av distinkta storcirklar som helst möts vid ett par antipodalpunkter; och
två distinkta par av antipoda punkter ligger på en enda stor cirkel.

Om vi identifierar varje punkt på sfären med dess antipodalpunkt, så får vi en representation av det verkliga projektiva planet där "punkterna" i det projektiva planet verkligen är punkter. Detta betyder att det projektiva planet är sfärens kvotutrymme som erhålls genom att dela upp sfären i ekvivalensklasser under ekvivalensrelationen ~, där x ~ y om y = x eller y = −x. Detta kvotutrymme för sfären är homeomorft med samlingen av alla linjer som passerar genom ursprunget i R ³ .

Kvotenskartan från sfären till det verkliga projektiva planet är i själva verket en täckande karta med två ark (dvs två-till-en) . Härav följer att grundgruppen för det reella projektiva planet är den cykliska gruppen av ordning 2; dvs heltal modulo 2. Man kan ta slingan AB från figuren ovan för att vara generatorn.

Den projektiva halvklotet

En halvklot kan representera ett verkligt projektivt plan genom att fästa motsatta punkter på ekvatorn tillsammans.

Eftersom sfären täcker det verkliga projektiva planet två gånger, kan planet representeras som en sluten halvklot runt vars kant motsatta punkter identifieras på liknande sätt.

Pojks yta – en fördjupning

Det projektiva planet kan nedsänkas (lokala kvarter i källrummet har inte självkorsningar) i 3-utrymme. Pojks yta är ett exempel på en nedsänkning.

Polyedriska exempel måste ha minst nio ytor.

romersk yta

En animation av den romerska ytan

Steiners romerska yta är en mer degenererad karta av det projektiva planet till 3-utrymme, innehållande en korsmössa .

Tetrahemihexaedern är en polyedrisk representation av det verkliga projektiva planet .

En polyedral representation är tetrahemihexahedronen , som har samma allmänna form som Steiners romerska yta, som visas här.

Hemi polyedra

Om man tittar i motsatt riktning kan vissa abstrakta regelbundna polytoper – hemi-cube , hemi-dodecahedron och hemi-icosahedron – konstrueras som regelbundna figurer i det projektiva planet; se även projektiva polyedrar .

Plana projektioner

Olika plana (platta) projektioner eller avbildningar av det projektiva planet har beskrivits. 1874 beskrev Klein kartläggningen:

k(x,y)=\left(1+x^{2}+y^{2}\right )^{\frac {1}{2}}{\begin{pmatrix}x\\y\end{pmatrix}}

Central projektion av den projektiva halvklotet på ett plan ger det vanliga oändliga projektiva planet, som beskrivs nedan.

Korsförsedd skiva

En sluten yta erhålls genom att limma en skiva på en korslock . Denna yta kan representeras parametriskt med följande ekvationer:

{\begin{aligned}X(u,v)&=r\,(1+\cos v)\,\cos u,\\Y(u,v)& =r\,(1+\cos v)\,\sin u,\\Z(u,v)&=-\operatörsnamn {tanh} \left(u-\pi \right)\,r\,\sin v,\end{aligned}}

där både u och v sträcker sig från 0 till 2 π .

Dessa ekvationer liknar de för en torus . Figur 1 visar en stängd skiva med korslock.

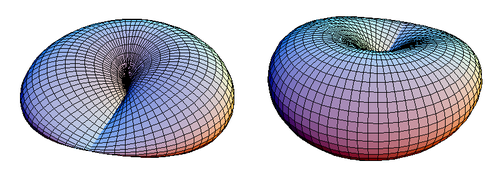
Figur 1. Två vyer av en skiva med korslock.

En korsad skiva har ett symmetriplan som passerar genom dess linjesegment av dubbla punkter. I figur 1 ses den korsade skivan ovanifrån dess symmetriplan z = 0, men den skulle se likadan ut om den ses underifrån.

En korsad skiva kan skäras upp längs dess symmetriplan, samtidigt som du ser till att inte skära längs någon av dess dubbla punkter. Resultatet visas i figur 2.

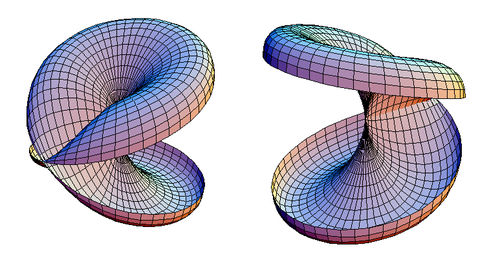
Figur 2. Två vyer av en skiva med korslock som har skurits upp.

När detta undantag väl har gjorts, kommer det att ses att den skivade, korsade skivan är homeomorf till en självkorsande skiva, som visas i figur 3.

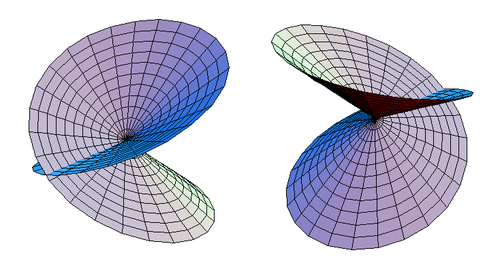
Figur 3. Två alternativa vyer av en självkorsande skiva.

Den självkorsande skivan är homeomorf till en vanlig skiva. De parametriska ekvationerna för den självkorsande skivan är:

{\begin{aligned} X(u,v)&=r\,v\,\cos 2u,\\Y(u,v)&=r\,v\,\sin 2u,\\Z(u,v)&=r\ ,v\,\cos u,\end{aligned}}

där u varierar från 0 till 2 π och v varierar från 0 till 1.

Att projicera den självkorsande skivan på symmetriplanet ( z = 0 i parametriseringen som gavs tidigare) som endast passerar genom de dubbla punkterna, blir resultatet en vanlig skiva som upprepar sig själv (fördubblar sig själv).

Planet z = 0 skär den självkorsande skivan till ett par skivor som är spegelreflektioner av varandra. Skivorna har centra vid ursprunget .

Betrakta nu skivornas fälgar (med v = 1). Punkterna på kanten av den självkorsande skivan kommer i par som är reflektioner av varandra med avseende på planet z = 0.

En korsad skiva bildas genom att identifiera dessa par av punkter, vilket gör dem likvärdiga med varandra. Detta betyder att en punkt med parametrar ( u , 1) och koordinater $(r\,\cos 2u,r\,\sin 2u, r\,\cos u)$ identifieras med punkten ( u + π, 1) vars koordinater är $(r\,\ cos 2u,r\,\sin 2u,-r\,\cos u)$ . Men detta betyder att par av motsatta punkter på kanten av den (motsvarande) vanliga skivan identifieras med varandra; så här bildas ett riktigt projektivt plan av en skiva. Därför är ytan som visas i figur 1 (tvärkåpa med skiva) topologiskt ekvivalent med det verkliga projektiva ^planet RP2 .

Homogena koordinater

Punkterna i planet kan representeras av homogena koordinater . En punkt har homogena koordinater [ x : y : z ], där koordinaterna [ x : y : z ] och [ tx : ty : tz ] anses representera samma punkt, för alla värden som inte är noll på t . Punkterna med koordinater [ x : y : 1] är det vanliga reella planet , som kallas den ändliga delen av det projektiva planet, och punkter med koordinater [ x : y : 0], som kallas punkter vid oändlighet eller idealpunkter , utgör en linje som kallas linjen i oändligheten . (De homogena koordinaterna [0 : 0 : 0] representerar ingen punkt.)

Linjerna i planet kan också representeras av homogena koordinater. En projektiv linje som motsvarar planet ax + by + cz = 0 i R ³ har de homogena koordinaterna ( a : b : c ). Således har dessa koordinater ekvivalensrelationen ( a : b : c ) = ( da : db : dc ) för alla värden som inte är noll på d . Därför ger en annan ekvation av samma linje dax + dby + dcz = 0 samma homogena koordinater. En punkt [ x : y : z ] ligger på en linje ( a : b : c ) om ax + by + cz = 0. Därför motsvarar linjer med koordinater ( a : b : c ) där a , b inte båda är 0 till linjerna i det vanliga reella planet , eftersom de innehåller punkter som inte är i oändlighet. Linjen med koordinater (0 : 0 : 1) är linjen i oändligheten, eftersom de enda punkterna på den är de med z = 0.

Punkter, linjer och plan

En linje i P ² kan representeras av ekvationen ax + by + cz = 0. Om vi behandlar a , b , och c som kolumnvektorn ℓ och x , y , z som kolumnvektorn x så kan ekvationen ovan vara skrivet i matrisform som:

x ^T ℓ = 0 eller ℓ ^T x = 0.

Med hjälp av vektornotation kan vi istället skriva x ⋅ ℓ = 0 eller ℓ ⋅ x = 0.

Ekvationen k ( x ^T ℓ ) = 0 (vilken k är en skalär som inte är noll) sveper ut ett plan som går genom noll i R ³ och k ( x ) sveper ut en linje, igen genom noll. Planet och linjen är linjära delrum i R ³ , som alltid går genom noll.

Idealiska poäng

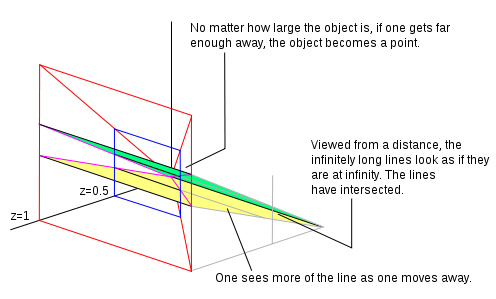
I P ² är ekvationen för en linje ax + by + cz = = 0 and this equation can represent a line on any plane parallel to the xy plane by multiplying the equation by k.

Om z = 1 har vi en normaliserad homogen koordinat. Alla punkter som har z = 1 skapar ett plan. Låt oss låtsas att vi tittar på det planet (från en position längre ut längs z- axeln och tittar tillbaka mot origo) och det finns två parallella linjer ritade på planet. Från där vi står (med tanke på vår visuella förmåga) kan vi bara se så mycket av planet, som vi representerar som området som är skisserat i rött i diagrammet. Om vi går bort från planet längs z -axeln, (fortfarande tittar bakåt mot origo), kan vi se mer av planet. I vårt synfält har ursprungliga punkter flyttats. Vi kan spegla denna rörelse genom att dividera den homogena koordinaten med en konstant. I den intilliggande bilden har vi dividerat med 2 så z -värdet nu blir 0,5. Om vi går tillräckligt långt bort blir det vi tittar på en punkt i fjärran. När vi går iväg ser vi mer och mer av de parallella linjerna. Linjerna kommer att mötas vid en linje i oändligheten (en linje som går genom noll på planet vid z = 0 ). Linjer på planet när z = 0 är idealpunkter. Planet vid z = 0 är linjen i oändligheten.

Den homogena punkten (0, 0, 0) är där alla verkliga punkter går när du tittar på planet från ett oändligt avstånd, en linje på z = 0 -planet är där parallella linjer skär varandra.

Dualitet

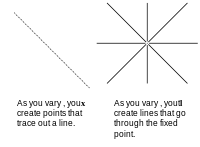
there are two column vectors I ekvationen x ^Tℓℓ = 0 = x constant and vary the coefficients ℓ we create new lines that go through the point. If we keep the coefficients constant and vary the points that satisfy the equation we create a line. We look upon x as a point, because the axes we are using are x, y, and z. If we instead plotted the coefficients using axis marked a, b, c points would become lines and lines would become points. If you prove something with the data plotted on axis marked x, y, and z the same argument can be used for the data plotted on axis marked a, b, and c. That is duality.

Linjer som sammanfogar punkter och skärningspunkter mellan linjer (med hjälp av dualitet)

Ekvationen x ^T ℓ = 0 beräknar den inre produkten av två kolumnvektorer. Den inre produkten av två vektorer är noll om vektorerna är ortogonala . I P ^{2 kan} linjen mellan punkterna x ₁ och x ₂ representeras som en kolumnvektor ℓ som uppfyller ekvationerna x ₁^T ℓ = 0 och x ₂^T ℓ = 0 , eller med andra ord en kolumnvektor ℓ som är ortogonal mot x ₁ och x ₂ . Korsprodukten kommer att hitta en sådan vektor: linjen som förenar två punkter har homogena koordinater som ges av ekvationen x ₁ × x ₂ . Skärningen av två linjer kan hittas på samma sätt, med hjälp av dualitet, som korsprodukten av vektorerna som representerar linjerna, ℓ ₁ × ℓ ₂ .

Inbäddning i 4-dimensionellt utrymme

Det projektiva planet bäddar in i det 4-dimensionella euklidiska rummet. Det verkliga projektiva planet P ² ( R ) är kvoten för tvåsfären

S ² = {( x , y , z ) ∈ R ³ : x ² + y ² + z ² = 1}

genom den antipoda relationen ( x , y , z ) ~ (− x , − y , − z ) . Betrakta funktionen R ³ → R ⁴ som ges av ( x , y , z ) ↦ ( xy , xz , y ² − z ² , 2 yz ) . Denna karta begränsar sig till en karta vars domän är S ² och eftersom varje komponent är ett homogent polynom med jämn grad, tar den samma värden i R ⁴ på var och en av två antipodalpunkter på S ² . Detta ger en karta P ² ( R ) → R ⁴ . Dessutom är den här kartan en inbäddning. Lägg märke till att denna inbäddning tillåter en projektion i R3 som är den ^romerska ytan .

Högre icke-orienterbara ytor

Genom att limma ihop projektiva plan successivt får vi icke-orienterbara ytor av högre demigenus . Limningsprocessen består av att skära ut en liten skiva från varje yta och identifiera ( limma ) deras gränscirklar. Genom att limma två projektiva plan skapas Klein-flaskan .

Artikeln om den grundläggande polygonen beskriver de högre icke-orienterbara ytorna.

Se även

Coxeter, HSM (1955), The Real Projective Plane , 2:a uppl. Cambridge: På University Press.
Reinhold Baer, Linear Algebra and Projective Geometry, Dover, 2005 ( ISBN 0-486-44565-8 )
Richter, David A., Two Models of the Real Projective Plane , hämtad 2010-04-15

externa länkar