Immersion (matematik)

Klein -flaskan , nedsänkt i 3-utrymmen.

I matematik är en nedsänkning en differentierbar funktion mellan differentierbara grenrör vars differential (eller pushforward) är injektiv överallt . Explicit f : M → N en nedsänkning om

D_{p}f:T_{p}M\to T_{f(p)}N\,

är en injektiv funktion vid varje punkt p i M (där T _p X betecknar tangentrymden för ett grenrör X i en punkt p i X ). På motsvarande sätt f en nedsänkning om dess derivata har konstant rang som är lika med dimensionen M :

\operatörsnamn {rank} \,D_{p}f=\dim M.

Funktionen f i sig behöver inte vara injektiv, bara dess derivata måste vara det.

Ett relaterat koncept är det med en inbäddning . En jämn inbäddning är en injektiv nedsänkning f : M → N som också är en topologisk inbäddning , så att M är diffeomorf till sin bild i N . En nedsänkning är just en lokal inbäddning – det vill säga för vilken punkt x ∈ M som helst finns det en grannskap , U ⊆ M , av x så att f : U → N är en inbäddning, och omvänt är en lokal inbäddning en nedsänkning. För oändliga dimensionella grenrör, anses detta ibland vara definitionen av en nedsänkning.

En injektivt nedsänkt undergren som inte är en inbäddning.

Om M är kompakt är en injektiv nedsänkning en inbäddning, men om M inte är kompakt behöver inte injektiva nedsänkningar vara inbäddningar; jämför med kontinuerliga bijektioner kontra homeomorfismer .

Vanlig homotopi

En regelbunden homotopi mellan två nedsänkningar f och g från ett grenrör M till ett grenrör N definieras som en differentierbar funktion H : M × [0,1] → N så att för alla t i [0, 1] funktionen H _t : M → N definierad av H _t ( x ) = H ( x , t ) för alla x ∈ M är en nedsänkning, med ₀ H = f , H ₁ = g . En vanlig homotopi är alltså en homotopi genom nedsänkningar.

Klassificering

Hassler Whitney initierade den systematiska studien av nedsänkningar och regelbundna homotopier på 1940-talet, vilket bevisade att för 2 m < n + 1 är varje karta f : M ^m → N ⁿ av ett m -dimensionellt grenrör till ett n -dimensionellt grenrör homotopiskt till en nedsänkning , och faktiskt till en inbäddning för 2 m < n ; dessa är Whitneys nedsänkningssats och Whitneys inbäddningssats .

Stephen Smale uttryckte de vanliga homotopiklasserna av nedsänkningar f : M ^m → Rn ^- som homotopigrupperna för en viss Stiefel manifold . Sfäreversionen var en särskilt slående konsekvens .

Morris Hirsch generaliserade Smales uttryck till en homotopi teoribeskrivning av de reguljära homotopiklasserna av nedsänkningar av varje m -dimensionellt grenrör M ^m i vilket n -dimensionellt grenrör N ^{n som helst} .

Hirsch-Smale-klassificeringen av nedsänkningar generaliserades av Mikhail Gromov .

Existens

Möbiusremsan fördjupar sig inte i kodimension 0 eftersom dess tangentknippe är icke-trivial .

Det primära hindret för existensen av en nedsänkning i : M ^m → R ⁿ är den stabila normala bunten av M , som detekteras av dess karakteristiska klasser , särskilt dess Stiefel-Whitney-klasser . Det vill säga, eftersom Rn är ^{parallelliserbar} , är tillbakadragningen av dess tangentknippe till M trivial ; eftersom denna pullback är den direkta summan av den (egendefinierade) tangentbunten på M , TM , som har dimensionen m , och av normalbunten ν av nedsänkningen i , som har dimensionen n − m , för att det ska finnas en samdimension k nedsänkning av M , måste det finnas ett vektorknippe med dimensionen k , ξ ^k , som står för den normala bunten ν , så att TM ⊕ ξ ^k är trivial. Omvänt, givet en sådan bunt, är en nedsänkning av M med denna normala bunt ekvivalent med en kodimension 0 nedsänkning av det totala utrymmet för denna bunt, som är ett öppet grenrör.

Den stabila normala bunten är klassen av normala buntar plus triviala buntar, och om den stabila normala bunten har kohomologisk dimension k , kan den inte komma från en (instabil) normal bunt med dimension mindre än k . Således är kohomologidimensionen av det stabila normala knippet, som detekteras av dess högsta icke-försvinnande karakteristiska klass, ett hinder för nedsänkningar.

Eftersom karakteristiska klasser multiplicerar under direktsumman av vektorbuntar, kan denna obstruktion anges i sig i termer av rymden M och dess tangentknippe och kohomologialgebra. Detta hinder uppgavs (i termer av tangentbunten, inte stabil normalbunt) av Whitney.

Till exempel har Möbius-remsan en icke-trivial tangentbunt, så den kan inte fördjupas i kodimension 0 (i R ² ), även om den bäddas in i kodimension 1 (i R ³ ).

William S. Massey ( 1960 ) visade att dessa karakteristiska klasser (Stiefel–Whitney-klasserna i det stabila normalknippet) försvinner över graden n − α ( n ) , där α ( n ) är antalet "1"-siffror när n är skrivet i binärt; denna gräns är skarp, vilket realiseras av verkligt projektivt utrymme . Detta gav bevis på nedsänkningsförmodan , nämligen att varje n -grenrör kunde nedsänkas i kodimensionen n − α ( n ) , dvs i R ^{2 n −α( n )} . Denna gissning bevisades av Ralph Cohen ( 1985 ).

Kodimension 0

0 Kodimension 0 nedsänkningar är likvärdiga relativa dimensioner nedsänkningar , och är bättre att se som nedsänkningar. En kodimension 0 nedsänkning av ett slutet grenrör är just en täckande karta , dvs ett fiberknippe med 0-dimensionell (diskret) fiber. Enligt Ehresmanns sats och Phillips sats om nedsänkningar är en korrekt nedsänkning av grenrör ett fiberknippe, därför beter sig kodimension/relativ dimension 0 nedsänkningar/nedsänkningar som nedsänkningar.

Vidare beter sig inte nedsänkningar av kodimension 0 som andra nedsänkningar, som till stor del bestäms av den stabila normala bunten: i kodimension 0 har man problem med grundläggande klass och täckutrymmen. Till exempel finns det ingen kodimension 0 nedsänkning S ¹ → R ¹ , trots att cirkeln är parallelliserbar, vilket kan bevisas eftersom linjen inte har någon grundläggande klass, så man får inte den erforderliga kartan på toppkohomologi. Alternativt är detta genom invarians av domän . På liknande sätt, även om S ³ och 3-torus T ³ båda är parallelliserbara, finns det ingen nedsänkning T ³ → S ³ – ett sådant lock skulle behöva förgrenas vid vissa punkter, eftersom sfären helt enkelt är ansluten.

Ett annat sätt att förstå detta är att en kodimension k nedsänkning av ett grenrör motsvarar en nedsänkning av en kodimension 0 av ett k -dimensionellt vektorknippe, vilket är ett öppet grenrör om samdimensionen är större än 0, men ett stängt grenrör i kodimension 0 ( om originalgrenröret är stängt).

Flera poäng

En k -tuppelpunkt (dubbel, trippel, etc.) av en nedsänkning f : M → N är en oordnad uppsättning { x ₁ , ..., x _k } av distinkta punkter x _i ∈ M med samma bild f ( x _i ) ∈ N . Om M är ett m -dimensionellt grenrör och N är ett n -dimensionellt grenrör då för en nedsänkning f : M → N i allmän position är uppsättningen av k -tupelpunkter ett ( n − k ( n − m )) -dimensionellt grenrör . Varje inbäddning är en nedsänkning utan flera punkter (där k > 1 ). Observera dock att det omvända är falskt: det finns injektiva nedsänkningar som inte är inbäddningar.

Naturen hos de multipla punkterna klassificerar nedsänkningar; till exempel klassificeras nedsänkningar av en cirkel i planet upp till vanlig homotopi efter antalet dubbelpunkter.

Vid en nyckelpunkt i kirurgiteorin är det nödvändigt att avgöra om en nedsänkning f : S ^m → N ^{2 m} av en m -sfär i ett 2 m -dimensionellt grenrör är regelbundet homotopiskt till en inbäddning, i vilket fall den kan dödas av kirurgi. Vägg associerad med f en invariant μ ( f ) i en kvot av den fundamentala gruppringen Z [ π $1$ ₍ N ) ] som räknar de dubbla punkterna för f i den universella täckningen av N . För m > 2 är f regelbunden homotopisk till en inbäddning om och endast om μ ( f ) = 0 enligt Whitney - tricket.

Man kan studera inbäddningar som "nedsänkningar utan flera punkter", eftersom nedsänkningar är lättare att klassificera. Således kan man utgå från nedsänkningar och försöka eliminera flera punkter, se om man kan göra detta utan att introducera andra singulariteter – studera "flera disjunktioner". Detta gjordes först av André Haefliger , och detta tillvägagångssätt är fruktbart i kodimension 3 eller mer – ur operationsteorin synvinkel är detta "hög (sam)dimension", till skillnad från kodimension 2 som är knutningsdimensionen, som i knut teori . Det studeras kategoriskt via " kalkylen för funktorer " av Thomas Goodwillie , John Klein och Michael S. Weiss .

Exempel och egenskaper

Quadrifolium , den 4-bladiga rosen.

En matematisk ros med k kronblad är en nedsänkning av cirkeln i planet med en enda k -tupelpunkt; k kan vara vilket udda tal som helst, men om jämnt måste vara en multipel av 4, så siffran 8, med k = 2, är inte en ros.
Klein -flaskan , och alla andra icke-orienterbara slutna ytor, kan sänkas ner i 3-utrymmen men inte bäddas in.
Genom Whitney–Graustein-satsen klassificeras de reguljära homotopiklasserna av nedsänkningar av cirkeln i planet efter slingrande numret , som också är antalet dubbelpunkter räknade algebraiskt (dvs. med tecken).
Sfären kan vändas ut och in : standardinbäddningen ₀ f : S ² → R ³ är relaterad till ₀ f ₁ = − f : S ² → R ³ genom en regelbunden homotopi av nedsänkningar f _t : S ² → R ³ .
Pojkens yta är en nedsänkning av det verkliga projektiva planet i 3-rum; alltså också en 2-till-1 nedsänkning av sfären.
Morinytan är en nedsänkning av sfären ; både den och Boys yta uppstår som mellanvägsmodeller i sfäreversion.

Pojkens yta
Morins yta

Nedsänkta plan kurvor

Denna kurva har total krökning 6

π

, och svängnummer 3, även om den bara har lindningsnummer 2 om p .

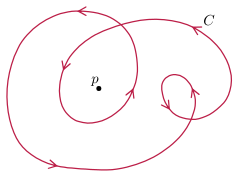
Nedsänkta plankurvor har ett väldefinierat svängtal , vilket kan definieras som den totala krökningen dividerat med 2 $π$ . Detta är oföränderligt under regelbunden homotopi, enligt Whitney-Graustein-satsen – topologiskt är det graden av Gauss-kartan , eller ekvivalent slingrande numret för enhetstangensen (som inte försvinner) om ursprunget. Vidare är detta en komplett uppsättning invarianter - två plankurvor med samma vändningsnummer är regelbundna homotopiska.

Varje nedsänkt plan kurva lyfts till en inbäddad rymdkurva genom att separera skärningspunkterna, vilket inte är sant i högre dimensioner. Med tillagd data (vilken tråd är överst) ger nedsänkta plankurvor knutdiagram , som är av centralt intresse inom knutteorin . Medan nedsänkta plankurvor, upp till vanlig homotopi, bestäms av deras vändningsnummer, har knutar en mycket rik och komplex struktur.

Nedsänkta ytor i 3-utrymmen

Studiet av nedsänkta ytor i 3-utrymme är nära förknippat med studiet av knutna (inbäddade) ytor i 4-utrymme, i analogi med teorin om knutdiagram ( nedsänkta plankurvor (2-rum) som projektioner av knutna kurvor i 3 -space): givet en knuten yta i 4-utrymme, kan man projicera den till en nedsänkt yta i 3-space, och omvänt, givet en nedsänkt yta i 3-space, kan man fråga om den lyfter till 4-space - är är det projektionen av en knuten yta i 4-utrymmen? Detta gör att man kan relatera frågor om dessa objekt.

Ett grundläggande resultat, i motsats till fallet med plana kurvor, är att inte varje nedsänkt yta lyfts till en knuten yta. I vissa fall är hindret 2-torsion, som i Koschorkes exempel , som är en nedsänkt yta (bildad av 3 Möbius-band, med en trippelspets ) som inte lyfter till en knuten yta, men den har ett dubbelt lock som gör det. hiss. En detaljerad analys ges i Carter & Saito (1998a) , medan en nyare undersökning ges i Carter, Kamada & Saito (2004) .

Generaliseringar

En långtgående generalisering av immersionsteorin är homotopiprincipen : man kan betrakta nedsänkningsvillkoret (rangen på derivatan är alltid k ) som en partiell differentialrelation (PDR), eftersom det kan anges i termer av partiella derivator av funktionen. Då är Smale–Hirsch immersionsteori resultatet att detta reduceras till homotopi-teori, och homotopiprincipen ger allmänna förutsättningar och skäl för PDR att reducera till homotopiteori.

Se även

Anteckningar

Adachi, Masahisa (1993), Inbäddningar och nedsänkningar , översatt av Kiki Hudson, ISBN 978-0-8218-4612-4
Arnold, VI ; Varchenko, AN; Gusein-Zade, SM (1985), Singularities of Differentiable Maps: Volym 1 , Birkhäuser, ISBN 0-8176-3187-9
Biskop, Richard Lawrence ; Crittenden, Richard J. (1964), Geometry of manifolds , New York: Academic Press, ISBN 978-0-8218-2923-3
Biskop, RL ; Goldberg, SI (1968), Tensor Analysis on Manifolds (First Dover 1980 ed.), The Macmillan Company, ISBN 0-486-64039-6
Bruce, JW; Giblin, PJ (1984), Curves and Singularities , Cambridge University Press, ISBN 0-521-42999-4
Carter, J. Scott; Saito, Masahico (1998a), "Ytor i 3-utrymme som inte lyfter till inbäddningar i 4-utrymme", Knot theory (Warszawa, 1995) , Banach Center Publ., vol. 42, polska acad. Sci., Warszawa, s. 29–47, CiteSeerX 10.1.1.44.1505 , MR 1634445 .
Carter, J. Scott; Saito, Masahico (1998), Knotted Surfaces and Their Diagrams , Mathematical Surveys and Monographs, vol. 55, sid. 258, ISBN 978-0-8218-0593-0
Carter, Scott; Kamada, Seiichi; Saito, Masahico (2004), Ytor i 4-rum , Encyclopaedia of Mathematical Sciences, vol. 142, Berlin: Springer-Verlag, doi : 10.1007/978-3-662-10162-9 , ISBN 3-540-21040-7 , MR 2060067 .
( 1985), "The immersion conjecture for differentiable manifolds", Annals of Mathematics , Second Series, 122 (2): 237–328, doi : 10.2307/1971304 , JSTOR 1971304 , 822080 .
Crampin, Michael; Pirani, Felix Arnold Edward (1994), Tillämplig differentialgeometri , Cambridge, England: Cambridge University Press, ISBN 978-0-521-23190-9
Darling, Richard William Ramsay (1994), Differential forms and connections , Cambridge, Storbritannien: Cambridge University Press, Bibcode : 1994dfc..book.....D , ISBN 978-0-521-46800-8 .
do Carmo, Manfredo Perdigao (1994), Riemannian Geometry , ISBN 978-0-8176-3490-2
Frankel, Theodore (1997), The Geometry of Physics , Cambridge: Cambridge University Press, ISBN 0-521-38753-1
Gallot, Sylvestre; Hulin, Dominique ; Lafontaine, Jacques (2004), Riemannian Geometry (3:e upplagan), Berlin, New York: Springer-Verlag , ISBN 978-3-540-20493-0
Gromov, M. (1986), Partial differential relations , Springer, ISBN 3-540-12177-3
Hirsch, Morris W. (1959), "Immersions of manifolds", Transactions of the American Mathematical Society , 93 (2): 242–276, doi : 10.2307/1993453 , JSTOR 1993453 , MR 0119214 .
Kobayashi, Shoshichi; Nomizu, Katsumi (1963), Foundations of Differential Geometry, Volym 1, New York: Wiley-Interscience
Koschorke, Ulrich (1979), "Multiple points of immersions, and the Kahn-Priddy theorem", Zeitschrift , 169 (3): 223–236, doi : 10.1007/BF01214837 , MR 0554526 , 822CID 3212CID 1212C Mathematische
Kosinski, Antoni Albert (2007) [1993], Differential manifolds , Mineola, New York: Dover Publications, ISBN 978-0-486-46244-8
Lang, Serge (1999), Fundamentals of Differential Geometry , Graduate Texts in Mathematics, New York: Springer, ISBN 978-0-387-98593-0
Massey, WS (1960), "On the Stiefel-Whitney classes of a manifold", American Journal of Mathematics , 82 (1): 92–102, doi : 10.2307/2372878 , JSTOR 2372878 , MR 0111053 .
Smale, Stephen (1958), "A classification of immersions of the two-sphere", Transactions of the American Mathematical Society , 90 (2): 281–290, doi : 10.2307/1993205 , JSTOR 1993205 , MR 0104227 .
Smale, Stephen (1959), "The classification of immersions of spheres in Euclidean spaces", Annals of Mathematics , Second Series, 69 (2): 327–344, doi : 10.2307/1970186 , JSTOR 1970186 , MR 710 .
Spivak, Michael (1999) [1970], A Comprehensive Introduction to differential geometry (Volume 1) , Publicera eller förgås, ISBN 0-914098-70-5
Spring, David (2005), "The golden age of immersion theory in topology: 1959–1973: A matematical survey from a historical perspective", Bulletin of the American Mathematical Society , New Series, 42 (2): 163–180, CiteSeerX 10.1.1.363.913 , doi : 10.1090/S0273-0979-05-01048-7 , MR 2133309 , S2CID 9237068 .
Szekeres, Peter (2004), En kurs i modern matematisk fysik: grupper, Hilberts rymd och differentialgeometri , Cambridge, Storbritannien: Cambridge University Press, ISBN 978-0-521-82960-1
Wall, CTC (1999), Surgery on compact manifolds (PDF) , Mathematical Surveys and Monographs, vol. 69 (andra upplagan), Providence, RI: American Mathematical Society, doi : 10.1090/surv/069 , ISBN 0-8218-0942-3 , MR 1687388 .

externa länkar

Nedsänkning vid Manifold Atlas
Nedsänkning av ett grenrör på Encyclopedia of Mathematics