Yta (topologi)

En öppen yta med x -, y - och z -konturer visas.

För en bredare täckning av detta ämne, se Yta (matematik) .

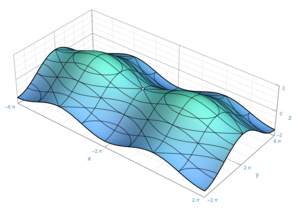
I den del av matematiken som kallas topologi är en yta ett tvådimensionellt mångfald . Vissa ytor uppstår som gränser för tredimensionella fasta ämnen; till exempel är sfären gränsen för den solida bollen. Andra ytor uppstår som grafer över funktioner för två variabler; se bilden till höger. Men ytor kan också definieras abstrakt, utan hänvisning till något omgivande utrymme . Till exempel Klein-flaskan en yta som inte kan bäddas in i det tredimensionella euklidiska rummet .

Topologiska ytor är ibland utrustade med ytterligare information, såsom en riemannisk metrik eller en komplex struktur, som kopplar dem till andra discipliner inom matematik, såsom differentialgeometri och komplex analys . De olika matematiska föreställningarna om yta kan användas för att modellera ytor i den fysiska världen.

I allmänhet

Ytterligare information: Yta (matematik)

Inom matematiken är en yta en geometrisk form som liknar ett deformerat plan . De mest välbekanta exemplen uppstår som gränser för fasta föremål i vanliga tredimensionella euklidiska rymden R ³ , såsom sfärer . Den exakta definitionen av en yta kan bero på sammanhanget. Typiskt, i algebraisk geometri , kan en yta korsa sig själv (och kan ha andra singulariteter ), medan det i topologi och differentialgeometri kanske inte.

En yta är ett tvådimensionellt utrymme ; detta betyder att en rörlig punkt på en yta kan röra sig i två riktningar (den har två frihetsgrader) . Med andra ord, runt nästan varje punkt finns det en koordinatlapp på vilken ett tvådimensionellt koordinatsystem definieras. Till exempel liknar jordens yta (helst) en tvådimensionell sfär , och latitud och longitud ger tvådimensionella koordinater på den (förutom vid polerna och längs den 180:e meridianen ).

Begreppet yta används ofta inom fysik , teknik , datorgrafik och många andra discipliner, främst när det gäller att representera ytorna på fysiska föremål. Till exempel, vid analys av de aerodynamiska egenskaperna hos ett flygplan är det centrala övervägandet luftflödet längs dess yta.

Definitioner och första exempel

En (topologisk) yta är ett topologiskt utrymme där varje punkt har en öppen grannskap som är homeomorf till någon öppen delmängd av det euklidiska planet E ² . Ett sådant område, tillsammans med motsvarande homeomorfism, är känt som ett ( koordinat)diagram . Det är genom detta diagram som grannskapet ärver standardkoordinaterna på det euklidiska planet. Dessa koordinater är kända som lokala koordinater och dessa homeomorphisms leder oss till att beskriva ytor som lokalt euklidiska .

I de flesta skrifter om ämnet antas det ofta, explicit eller underförstått, att som ett topologiskt utrymme en yta också är icke-tom, sekund-räknalig , och Hausdorff . Det antas också ofta att ytorna i fråga hänger ihop.

Resten av den här artikeln kommer att anta, om inte annat anges, att en yta är icke-tom, Hausdorff, sekundräknbar och ansluten.

Mer generellt är en (topologisk) yta med gräns ett Hausdorff- topologiskt utrymme där varje punkt har en öppen grannskap som är homeomorf till någon öppen delmängd av stängningen av det övre halvplanet H ² i C . Dessa homeomorphisms är också kända som (koordinat) diagram . Gränsen för det övre halvplanet är x -axeln. En punkt på ytan avbildad via ett diagram till x -axeln kallas en gränspunkt . Samlingen av sådana punkter är känd som gräns , som nödvändigtvis är ett grenrör, det vill säga föreningen av slutna kurvor. Å andra sidan är en punkt som är mappad ovanför x -axeln en inre punkt . Samlingen av inre punkter är det inre av ytan som alltid är icke- tom . Den slutna skivan är ett enkelt exempel på en yta med gräns. Skivans gräns är en cirkel.

Termen yta som används utan kvalifikationer syftar på ytor utan gräns. I synnerhet är en yta med tom gräns en yta i vanlig mening. En yta med tom gräns som är kompakt är känd som en "stängd" yta. Den tvådimensionella sfären, den tvådimensionella torusen och det verkliga projektiva planet är exempel på slutna ytor.

Möbiusremsan är en yta på vilken distinktionen mellan medurs och moturs kan definieras lokalt, men inte globalt . I allmänhet sägs en yta vara orienterbar om den inte innehåller en homeomorf kopia av Möbiusremsan; intuitivt har den två distinkta "sidor". Till exempel är sfären och torus orienterbara, medan det verkliga projektiva planet inte är det (eftersom det verkliga projektiva planet med en punkt borttagen är homeomorft till den öppna Möbiusremsan).

I differentiell och algebraisk geometri läggs extra struktur till på ytans topologi. Denna tillagda struktur kan vara en jämnhetsstruktur (gör det möjligt att definiera differentierbara kartor till och från ytan), en Riemannisk metrik (gör det möjligt att definiera längd och vinklar på ytan), en komplex struktur (gör det möjligt att definiera holomorf kartor till och från ytan - i vilket fall ytan kallas en Riemann-yta ), eller en algebraisk struktur (gör det möjligt att upptäcka singulariteter , såsom självskärningar och cusps, som inte kan beskrivas enbart i termer av den underliggande topologin ).

Extrinsiskt definierade ytor och inbäddningar

En sfär kan definieras parametriskt (med x = r sin θ cos φ , y = r sin θ sin φ , z = r cos θ ) eller implicit (av x ² + y ² + z ² − r ² = 0 .)

Historiskt sett definierades ytor ursprungligen som underrum till euklidiska utrymmen. Ofta var dessa ytor nollställena för vissa funktioner , vanligtvis polynomfunktioner . En sådan definition betraktade ytan som en del av ett större (euklidiskt) utrymme, och betecknades som sådan extrinsisk .

I föregående avsnitt definieras en yta som ett topologiskt utrymme med vissa egenskaper, nämligen Hausdorff och lokalt euklidiskt. Detta topologiska utrymme anses inte vara ett underrum till ett annat utrymme. I denna mening är definitionen ovan, som är den definition som matematiker använder för närvarande, inneboende .

En yta definierad som inneboende krävs inte för att tillfredsställa den extra begränsningen att vara ett delrum av det euklidiska rummet. Det kan tyckas möjligt att vissa ytor som definieras i sig inte är ytor i yttre mening. Emellertid Whitneys inbäddningssats att varje yta faktiskt kan inbäddas homeomorfiskt i det euklidiska rummet, faktiskt i E ⁴ : De yttre och inneboende tillvägagångssätten visar sig vara likvärdiga.

^en gräns kan bäddas in i E3 ; å andra sidan kan det verkliga projektiva planet, som är kompakt, icke-orienterbart och utan gräns, inte bäddas in i E ³ (se Gramain). Steiner ytor , inklusive Boy's yta , den romerska ytan och cross-cap , är modeller av det verkliga projektiva planet i E ³ , men bara Boy ytan är en nedsänkt yta . Alla dessa modeller är singulära vid punkter där de skär sig själva.

Alexanderhornsfären är en välkänd patologisk inbäddning av tvåsfären i tresfären .

En knuten torus.

Den valda inbäddningen (om någon) av en yta i ett annat utrymme betraktas som yttre information; det är inte nödvändigt för själva ytan. Till exempel kan en torus bäddas in i E ³ på "standard" sätt (som ser ut som en bagel ) eller på ett knutet sätt (se figur). De två inbäddade tori är homeomorfa, men inte isotopiska : De är topologiskt likvärdiga, men deras inbäddningar är det inte.

Bilden av en kontinuerlig, injektiv funktion från R2 ^till högre dimensionell Rn sägs vara en parametrisk yta ^. En sådan bild kallas så eftersom x - och y - riktningarna för domänen R ² är 2 variabler som parametriserar bilden. En parametrisk yta behöver inte vara en topologisk yta. En rotationsyta kan ses som en speciell typ av parametrisk yta.

Om f är en jämn funktion från R ³ till R vars gradient inte är noll, så definierar nollpunkten för f en yta, känd som en implicit yta . Om villkoret för icke-försvinnande gradient sjunker, kan nollstället utveckla singulariteter.

Konstruktion från polygoner

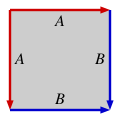
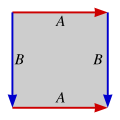
Varje stängd yta kan konstrueras från en orienterad polygon med ett jämnt antal sidor, kallad en fundamental polygon av ytan, genom parvis identifiering av dess kanter. Till exempel, i varje polygon nedan, att fästa sidorna med matchande etiketter ( A med A , B med B ), så att pilarna pekar i samma riktning, ger den angivna ytan.

• 

  sfär

• 

  verkligt projektivt plan

• 

  torus

• 

  Klein flaska

Vilken fundamental polygon som helst kan skrivas symboliskt enligt följande. Börja vid vilken vertex som helst och fortsätt runt polygonens omkrets i endera riktningen tills du återvänder till startpunkten. Under denna genomgång, anteckna etiketten på varje kant i ordning, med exponenten -1 om kanten pekar mot tvärriktningen. De fyra ovanstående modellerna ger efter, när de körs medurs med början i det övre vänstra hörnet

• sfär: $ABB^{-1}A^{-1}$
• verkligt projektivt plan: $ABAB$
• torus: $ABA^{-1}B^{-1}$
• Klein flaska: $ABAB^{-1}$ .

Observera att sfären och det projektiva planet båda kan realiseras som kvoter av 2-gon, medan torus och Klein-flaskan kräver en 4-gon (fyrkant).

Det sålunda härledda uttrycket från en fundamental polygon av en yta visar sig vara den enda relationen i en presentation av ytans fundamentala grupp med polygonkantetiketterna som generatorer. Detta är en konsekvens av Seifert–van Kampens sats .

Limning av kanter på polygoner är en speciell typ av kvotrymdprocess . Kvotientbegreppet kan tillämpas mer generellt för att producera nya eller alternativa konstruktioner av ytor. Till exempel kan det verkliga projektiva planet erhållas som sfärens kvot genom att identifiera alla par av motsatta punkter på sfären. Ett annat exempel på en kvot är den sammankopplade summan.

Anslutna summor

Den sammankopplade summan av två ytor M och N , betecknade M # N , erhålls genom att ta bort en skiva från var och en av dem och limma dem längs gränskomponenterna som blir resultatet. Gränsen för en skiva är en cirkel, så dessa gränskomponenter är cirklar. Euler -karakteristiken $\chi$ av M # N är summan av Euler-karakteristiken för summanterna, minus två:

$\chi (M{\mathbin {\#}}N)=\chi (M)+\chi (N)-2 .\,$

Sfären S är ett identitetselement för den sammankopplade summan, vilket betyder att S # M = M . Detta beror på att ta bort en skiva från sfären lämnar en skiva, som helt enkelt ersätter den skiva som raderades från M vid limning.

Kopplad summering med torus T beskrivs också som att fästa ett "handtag" till den andra summan M . Om M är orienterbar så är T # M också det . Den sammankopplade summan är associativ, så den sammankopplade summan av en ändlig samling ytor är väldefinierad.

Den sammankopplade summan av två verkliga projektiva plan, P # P , är Klein-flaskan K . Den sammankopplade summan av det verkliga projektiva planet och Klein-flaskan är homeomorf till den sammankopplade summan av det verkliga projektiva planet med torus; i en formel, P # K = P # T . Således är den sammankopplade summan av tre verkliga projektiva plan homeomorf till den sammankopplade summan av det verkliga projektiva planet med torus. Varje sammankopplad summa som involverar ett verkligt projektivt plan är icke-orienterbar.

Slutna ytor

"Öppen yta" omdirigerar hit. Ej att förväxla med fri yta .

En sluten yta är en yta som är kompakt och utan gräns . Exempel på slutna ytor är sfären , torus och Klein- flaskan . Exempel på icke-slutna ytor inkluderar en öppen skiva (som är en sfär med en punktering ), en cylinder (som är en sfär med två punkteringar) och Möbius-remsan .

En yta inbäddad i det tredimensionella rummet är stängd om och endast om det är gränsen för ett fast ämne. Som med alla slutna grenrör , är en yta inbäddad i det euklidiska rymden som är stängd med avseende på den nedärvda euklidiska topologin inte nödvändigtvis en sluten yta; till exempel är en skiva inbäddad i $\mathbb {R} ^{3}$ som innehåller dess gräns en yta som är topologiskt stängd men inte en sluten yta.

Klassificering av slutna ytor

Några exempel på orienterbara slutna ytor (vänster) och ytor med gräns (höger). Vänster: Vissa orienterbara slutna ytor är ytan på en sfär, ytan på en torus och ytan på en kub. (Kuben och sfären är topologiskt ekvivalenta med varandra.) Höger: Vissa ytor med gräns är skivytan , kvadratisk yta och hemisfärytan. Gränserna visas i rött. Alla dessa tre är topologiskt likvärdiga med varandra.

Klassificeringssatsen för slutna ytor säger att varje ansluten sluten yta är homeomorf för någon medlem av en av dessa tre familjer:

1. sfären , _
2. den anslutna summan av g tori för g ≥ 1,
3. den sammankopplade summan av k verkliga projektiva plan för k ≥ 1.

Ytorna i de två första familjerna är orienterbara . Det är bekvämt att kombinera de två familjerna genom att betrakta sfären som den sammankopplade summan av 0 tori. Antalet g involverade tori kallas ytans släkte . Sfären och torus har Eulerkarakteristika 2 respektive 0, och i allmänhet är Eulerkarakteristiken för den sammankopplade summan av g tori 2 − 2 g .

Ytorna i den tredje familjen är icke-orienterbara. Eulerkarakteristiken för det verkliga projektiva planet är 1, och i allmänhet är Eulerkarakteristiken för den sammankopplade summan av k av dem 2 − k .

Det följer att en sluten yta bestäms, fram till homeomorfism, av två delar av information: dess Euler-karaktär, och om den är orienterbar eller inte. Med andra ord, Eulers egenskaper och orienterbarhet klassificerar helt slutna ytor upp till homeomorfism.

Slutna ytor med flera anslutna komponenter klassificeras efter klassen för var och en av deras anslutna komponenter, och därför antar man generellt att ytan är ansluten.

Monoid struktur

När man relaterar denna klassificering till sammankopplade summor, bildar de slutna ytorna fram till homeomorfism en kommutativ monoid under driften av sammankopplade summor, liksom grenrör av vilken fast dimension som helst. Identiteten är sfären, medan det verkliga projektiva planet och torus genererar denna monoid, med en enda relation P # P # P = P # T , som också kan skrivas P # K = P # T , eftersom K = P # P . Detta förhållande är ibland känt som Dycks sats efter Walther von Dyck , som bevisade det i ( Dyck 1888 ), och den tredubbla korsytan P # P # P kallas följaktligen Dycks yta .

Geometriskt lägger connect-sum med en torus ( # T ) ett handtag med båda ändarna fästa på samma sida av ytan, medan connect-sum med en Klein-flaska ( # K ) lägger till ett handtag med de två ändarna fästa på motsatta sidor av en orienterbar yta; i närvaro av ett projektivt plan ( # P ), är ytan inte orienterbar (det finns ingen uppfattning om sida), så det finns ingen skillnad mellan att fästa en torus och att fästa en Klein-flaska, vilket förklarar sambandet.

Bevis

Klassificeringen av slutna ytor har varit känd sedan 1860-talet och idag finns det ett antal bevis.

Topologiska och kombinatoriska bevis i allmänhet förlitar sig på det svåra resultatet att varje kompakt 2-grenrör är homeomorf till ett förenklat komplex , vilket är av intresse i sig. Det vanligaste beviset för klassificeringen är ( Seifert & Threlfall 1934 ) , som för varje triangulerad yta till en standardform. Ett förenklat bevis, som undviker en standardform, upptäcktes av John H. Conway cirka 1992, som han kallade "Zero Irrelevancy Proof" eller "ZIP proof" och presenteras i ( Francis & Weeks 1999 ) .

Ett geometriskt bevis, som ger ett starkare geometriskt resultat, är uniformiseringssatsen . Detta bevisades ursprungligen endast för Riemann ytor på 1880- och 1900-talen av Felix Klein, Paul Koebe och Henri Poincaré .

Ytor med gräns

Kompakta ytor, eventuellt med avgränsning, är helt enkelt slutna ytor med ett begränsat antal hål (öppna skivor som tagits bort). Således klassificeras en sammankopplad kompakt yta efter antalet gränskomponenter och släktet för motsvarande slutna yta - på motsvarande sätt efter antalet gränskomponenter, orienterbarheten och Euler-karakteristiken. Släktet för en kompakt yta definieras som släktet för motsvarande slutna yta.

Denna klassificering följer nästan omedelbart av klassificeringen av slutna ytor: att ta bort en öppen skiva från en sluten yta ger en kompakt yta med en cirkel för gränskomponent, och borttagning av k öppna skivor ger en kompakt yta med k disjunkta cirklar för gränskomponenter. De exakta placeringarna av hålen är irrelevanta, eftersom homeomorfismgruppen verkar k -transitivt på alla anslutna grenrör med dimensioner på minst 2.

Omvänt är gränsen för en kompakt yta ett slutet 1-grenrör, och är därför den disjunkta föreningen av ett ändligt antal cirklar; att fylla dessa cirklar med skivor (formellt ta konen ) ger en sluten yta.

Den unika kompakta orienterbara ytan av släktet g och med k gränskomponenter betecknas ofta $\Sigma _{g,k},$ till exempel i studiet av kartläggningsklassgruppen .

Icke-kompakta ytor

Icke-kompakta ytor är svårare att klassificera. Som ett enkelt exempel kan en icke-kompakt yta erhållas genom att punktera (ta bort en ändlig uppsättning punkter från) ett slutet grenrör. Å andra sidan är varje öppen delmängd av en kompakt yta i sig en icke-kompakt yta; överväg till exempel komplementet till en Cantor-uppsättning i sfären, även känd som Cantor-trädytan . Men inte varje icke-kompakt yta är en delmängd av en kompakt yta; två kanoniska motexempel är Jacobs stege och Loch Ness-monstret , som är icke-kompakta ytor med oändligt släkte.

En icke-kompakt yta M har ett icke-tomt utrymme av ändarna E ( M ), vilket informellt sett beskriver hur ytan "går bort till oändligheten". Mellanrummet E ( M ) är alltid topologiskt ekvivalent med ett slutet delrum i Cantor-uppsättningen . M kan ha ett ändligt eller countably oändligt antal N _h av handtag, såväl som ett ändligt eller countably oändligt antal N _p av projektiva plan . Om både N _h och N _p är ändliga, så klassificerar dessa två tal, och den topologiska typen av ändrum, ytan M upp till topologisk ekvivalens. Om endera eller båda av N _h och N _p är oändliga, beror den topologiska typen av M inte bara på dessa två tal utan också på hur de oändliga närmar sig ändarnas utrymme. I allmänhet bestäms den topologiska typen av M av de fyra underrymden av E ( M ) som är gränspunkter för oändligt många handtag och oändligt många projektiva plan, gränspunkter för endast handtag, gränspunkter för endast projektiva plan och gränspunkter för ingendera .

Antagande om andraräknebarhet

Om man tar bort antagandet om andra räknebarhet från definitionen av en yta, finns det (nödvändigtvis icke-kompakta) topologiska ytor som inte har någon räknebar bas för sin topologi. Det kanske enklaste exemplet är den kartesiska produkten av den långa linjen med utrymmet för reella tal.

En annan yta som inte har någon räknebar bas för sin topologi, men som inte kräver valets Axiom för att bevisa dess existens, är Prüfer-manifoldet , som kan beskrivas med enkla ekvationer som visar att det är en realanalytisk yta. Prüfer-grenröret kan ses som det övre halvplanet tillsammans med en extra "tunga" T _x som hänger ner från den direkt under punkten ( x ,0), för varje verkligt x .

År 1925 bevisade Tibor Radó att alla Riemann-ytor (dvs. endimensionella komplexa grenrör ) nödvändigtvis är sekundräknbara ( Radós sats) . Om man däremot ersätter de reella talen i konstruktionen av Prüfer-ytan med de komplexa talen, erhåller man ett tvådimensionellt komplext grenrör (som nödvändigtvis är ett 4-dimensionellt reellt grenrör) utan någon räknebar bas.

Ytor i geometri

Huvudartikel: Differentialgeometri för ytor

Polyedrar , såsom gränsen för en kub , är bland de första ytorna som möts i geometri. Det är också möjligt att definiera släta ytor , där varje punkt har en diffeomorf grannskap till någon öppen uppsättning i E ² . Denna utarbetning gör att kalkyl kan appliceras på ytor för att bevisa många resultat.

Två släta ytor är diffeomorfa om och endast om de är homeomorfa. (Det analoga resultatet gäller inte för grenrör med högre dimensioner.) Sålunda klassificeras slutna ytor upp till diffeomorfism genom deras Euler-egenskaper och orienterbarhet.

Släta ytor utrustade med Riemannisk metrik är av grundläggande betydelse i differentialgeometri . En Riemannisk metrisk ger en yta med föreställningar om geodetisk , avstånd , vinkel och area. Det ger också upphov till Gaussisk krökning , som beskriver hur böjd eller böjd ytan är vid varje punkt. Krökning är en stel, geometrisk egenskap, eftersom den inte bevaras av allmänna diffeomorfismer på ytan. Den berömda Gauss-Bonnet-satsen för slutna ytor säger dock att integralen av den Gaussiska krökningen K över hela ytan S bestäms av Euler-karakteristiken:

$\int _{S}K\;dA=2\pi \chi (S).$

Detta resultat exemplifierar det djupa förhållandet mellan geometrin och topologin hos ytor (och, i mindre utsträckning, flerdimensionella grenrör).

Ett annat sätt på vilket ytor uppstår i geometrin är genom att passera in i den komplexa domänen. Ett komplext engrenrör är en slät orienterad yta, även kallad Riemann-yta . Varje komplex icke-singular algebraisk kurva som ses som ett komplext grenrör är en Riemann-yta. Faktum är att varje kompakt orienterbar yta kan realiseras som en Riemann-yta. Sålunda kännetecknas kompakta Riemannytor topologiskt av sitt släkte: 0, 1, 2, .... Å andra sidan karaktäriserar släktet inte den komplexa strukturen. Till exempel finns det oräkneligt många icke-isomorfa kompakta Riemann-ytor av släkte 1 (de elliptiska kurvorna) .

Komplexa strukturer på en sluten orienterad yta motsvarar konforma ekvivalensklasser av Riemannska metriker på ytan. En version av uniformiseringssatsen (på grund av Poincaré ) säger att varje Riemannisk mått på en orienterad, stängd yta är konformt likvärdig med ett i huvudsak unikt mått av konstant krökning . Detta ger en utgångspunkt för ett av synsätten till Teichmüller-teorin , som ger en finare klassificering av Riemann-ytor än den topologiska av enbart Euler-karaktäristik.

En komplex yta är ett komplext två-grenrör och därmed ett verkligt fyra-grenrör; det är inte en yta i den här artikelns mening. Inte heller definieras algebraiska kurvor över fält än de komplexa talen, och inte heller är algebraiska ytor definierade över andra fält än de reella talen.

Se även

• Gräns ​​(topologi)
• Volymform , för volymer av ytor i E ⁿ
• Poincaré metrisk , för metriska egenskaper hos Riemann-ytor
• romersk yta
• Pojkens yta
• Tetrahemihexahedron
• Skrynklig yta , en icke differentierbar yta som erhålls genom att deformera (krympa) en differentierbar yta

Anteckningar

•   Dyck, Walther (1888), "Beiträge zur Analysis situs I", Math. Ann. , 32 (4): 459–512, doi : 10.1007/bf01443580 , S2CID 118123073

Enkla bevis för klassificering upp till homeomorfism

•   Seifert, Herbert; Threlfall, William (1980), A textbook of topology , Pure and Applied Mathematics, vol. 89, Academic Press, ISBN 0126348502 , engelsk översättning av 1934 års klassiska tyska lärobok
• Ahlfors, Lars V.; Sario, Leo (1960), Riemann ytor , Princeton Mathematical Series, vol. 26, Princeton University Press , kapitel I
•   Maunder, CRF (1996), Algebraisk topologi , Dover Publications, ISBN 0486691314 , Cambridge grundkurs
•   Massey, William S. (1991). En grundkurs i algebraisk topologi . Springer-Verlag. ISBN 0-387-97430-X .
•   Bredon, Glen E. (1993). Topologi och geometri . Springer-Verlag. ISBN 0-387-97926-3 .
•   Jost, Jürgen (2006), Compact Riemann-ytor: en introduktion till samtida matematik (3:e upplagan), Springer, ISBN 3540330658 , för slutna orienterade Riemann-grenrör

Morse-teoretiska bevis för klassificering upp till diffeomorfism

• Hirsch, M. (1994), Differential topology (2nd ed.), Springer
•   Gauld, David B. (1982), Differential topology: an introduction , Monographs and Textbooks in Pure and Applied Mathematics, vol. 72, Marcel Dekker, ISBN 0824717090
•   Shastri, Anant R. (2011), Elements of differential topology , CRC Press, ISBN 9781439831601 , noggrant bevis riktat mot studenter
•   Gramain, André (1984). Topologi av ytor . BCS Associates. ISBN 0-914351-01-X . (Original 1969-70 Orsay kursanteckningar på franska för "Topologie des Surfaces")
• A. Champanerkar; et al., Klassificering av ytor via Morse Theory (PDF) , en utläggning av Gramains anteckningar {{ citation }} : CS1 underhåll: efterskrift ( länk )

Andra bevis

•   Lawson, Terry (2003), Topology: a geometric approach , Oxford University Press, ISBN 0-19-851597-9 , liknande morse-teoretiska bevis med hjälp av skjutbara handtag
•   Francis, George K.; Weeks, Jeffrey R. (maj 1999), "Conway's ZIP Proof" (PDF) , American Mathematical Monthly , 106 (5): 393, doi : 10.2307/2589143 , JSTOR 2589143 , arkiverad från originalet 2 (PDF) -0 -12, sida som diskuterar uppsatsen: On Conways ZIP Proof {{ citation }} : Extern länk i |postscript= ( hjälp ) CS1 underhåll: postscript ( länk )
•   Thomassen, Carsten (1992), "Jordan-Schönflies teorem och klassificeringen av ytor", Amer. Matematik. Monthly , 99 (2): 116–13, doi : 10.2307/2324180 , JSTOR 2324180 , kort elementärt bevis med spännande grafer
•   Prasolov, VV (2006), Elements of combinatorial and differential topology , Graduate Studies in Mathematics, vol. 74, American Mathematical Society, ISBN 0821838091 , innehåller en kort redogörelse för Thomassens bevis

externa länkar

• Klassificering av kompakta ytor i Mathifold Project
• Klassificeringen av ytor och Jordan Curve Theorem på hemsidan för Andrew Ranicki
• Math Surfaces Gallery, med 60 ~ytor och Java-applet för live-rotationsvisning
• Math Surfaces Animation, med JavaScript (Canvas HTML) för visning av tio ytor med rotation
• Klassificeringen av ytor Föreläsningsanteckningar av Z.Fiedorowicz
• Ytors historia och konst och deras matematiska modeller
• 2-grenrör vid Manifold Atlas