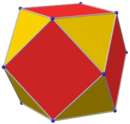
Arkimedisk solid

Trunkerad tetraeder , cuboctahedron och trunkerad icosidodecahedron . Den första och den sista kan beskrivas som den minsta respektive den största arkimediska soliden.

Rhombicuboctahedron och pseudo-rhombicuboctahedron

Inom geometrin är en arkimedisk fast substans en av de 13 fasta ämnen som först räknades upp av Arkimedes . De är de konvexa likformiga polyedrarna som består av regelbundna polygoner som möter i identiska hörn , exklusive de fem platoniska soliderna (som är sammansatta av endast en typ av polygon), exklusive prismorna och antiprismorna , och exklusive pseudorhombicuboctahedronen . De är en delmängd av Johnson solids , vars regelbundna polygonala ytor inte behöver mötas i identiska hörn.

"Identiska hörn" betyder att varje två hörn är symmetriska med varandra: En global isometri av hela det fasta ämnet tar en vertex till den andra samtidigt som det fasta ämnet läggs direkt på dess initiala position. Branko Grünbaum ( 2009 ) observerade att en 14:e polyeder, den långsträckta kvadratiska gyrobicupola (eller pseudo-rhombicuboctahedron), uppfyller en svagare definition av ett arkimedisk fast ämne, där "identiska hörn" bara betyder att ytorna som omger varje vertex är av samma typ (dvs varje vertex ser likadant ut på nära håll), så endast en lokal isometri krävs. Grünbaum påpekade ett vanligt fel där författarna definierar arkimediska fasta ämnen med denna lokala definition men utelämnar den 14:e polyedern. Om endast 13 polyedrar ska listas måste definitionen använda globala symmetrier för polyedern snarare än lokala grannskap.

Prismor och antiprismor , vars symmetrigrupper är dihedralgrupperna , anses i allmänhet inte vara arkimediska fasta ämnen, även om deras ansikten är regelbundna polygoner och deras symmetrigrupper agerar transitively på deras hörn. Exklusive dessa två oändliga familjer finns det 13 arkimediska fasta ämnen. Alla arkimediska fasta ämnen (men inte den långsträckta kvadratiska gyrobicupolan) kan göras via Wythoff-konstruktioner från de platoniska fasta kropparna med tetraedrisk , oktaedrisk och icosaedrisk symmetri .

Namnets ursprung

De arkimedeiska fasta kropparna har fått sitt namn från Arkimedes , som diskuterade dem i ett nu förlorat verk. Pappus hänvisar till det och säger att Arkimedes listade 13 polyedrar. Under renässansen värderade konstnärer och matematiker rena former med hög symmetri, och omkring 1620 hade Johannes Kepler slutfört återupptäckten av de 13 polyedrarna, samt definiera prismorna , antiprismorna och de icke-konvexa fasta ämnen som kallas Kepler-Poinsot polyedra . . (Se Schreiber, Fischer & Sternath 2008 för mer information om återupptäckten av arkimedeiska fasta ämnen under renässansen.)

Kepler kan också ha hittat den långsträckta fyrkantiga gyrobicupolan (pseudorhombicuboctahedron): åtminstone uppgav han en gång att det fanns 14 arkimedeiska fasta ämnen. Men hans publicerade uppräkning inkluderar bara de 13 enhetliga polyedrarna, och det första tydliga uttalandet om pseudorhombicuboctahedrons existens gjordes 1905 av Duncan Sommerville .

Klassificering

Det finns 13 arkimediska fasta kroppar (den långsträckta fyrkantiga gyrobicupolan räknas inte med ; 15 om spegelbilderna av två enantiomorfer , snubbkuben och snubbdodekaedern, räknas separat).

Här hänvisar vertexkonfigurationen till typen av regelbundna polygoner som möts vid en given vertex. Till exempel betyder en vertexkonfiguration på 4.6.8 att en kvadrat , hexagon och oktagon möts vid en vertex (med ordningen medsols runt vertexen).

Namn/ (alternativt namn)	Schläfli Coxeter	Transparent	Fast	Netto	Vertex konf. / fig.	Ansikten		Kanter	Vert.	Volym (enhetskanter)	Punktgrupp _	Sfäricitet
Trunkerad tetraeder	t{3,3}				3.6.6	8	4 trianglar 4 hexagoner	18	12	2,710 576	T d	0,775 4132
Cuboctahedron (rhombitetratetrahedron, triangulär gyrobicupola)	r{4,3} eller rr{3,3} eller				3.4.3.4	14	8 trianglar 6 rutor	24	12	2,357 023	O h	0,904 9972
Stympad kub	t{4,3}				3.8.8	14	8 trianglar 6 oktagoner	36	24	13 599 663	O h	0,849 4937
Trunkerad oktaeder (stympad tetratetraeder)	t{3,4} eller tr{3,3} eller				4.6.6	14	6 rutor 8 hexagoner	36	24	11.313 709	O h	0,909 9178
Rhombicuboctahedron (liten rhombicuboctahedron, långsträckt fyrkantig ortobicupola)	rr{4,3}				3.4.4.4	26	8 trianglar 18 rutor	48	24	8,714 045	O h	0,954 0796
Stympad cuboctahedron (stor rhombicuboctahedron)	tr{4,3}				4.6.8	26	12 rutor 8 hexagoner 6 oktagoner	72	48	41 798 990	O h	0,943 1657
Snub kub (snub cuboctahedron)	sr{4,3}				3.3.3.3.4	38	32 trianglar 6 rutor	60	24	7 889 295	O	0,965 1814
Icosidodecahedron (pentagonal gyrobirotunda)	r{5,3}				3.5.3.5	32	20 trianglar 12 femhörningar	60	30	13.835 526	jag h	0,951 0243
Stympad dodekaeder	t{5,3}				3.10.10	32	20 trianglar 12 dekagoner	90	60	85,039 665	jag h	0,926 0125
Stympad icosahedron	t{3,5}				5.6.6	32	12 femhörningar 20 sexhörningar	90	60	55,287 731	jag h	0,966 6219
Rhombicosidodecahedron (liten rhombicosidodecahedron)	rr{5,3}				3.4.5.4	62	20 trianglar 30 rutor 12 femhörningar	120	60	41,615 324	jag h	0,979 2370
Trunkerad icosidodecahedron (stor rhombicosidodecahedron)	tr{5,3}				4.6.10	62	30 rutor 20 hexagoner 12 dekagoner	180	120	206,803 399	jag h	0,970 3127
Snub dodecahedron (snub icosidodecahedron)	sr{5,3}				3.3.3.3.5	92	80 trianglar 12 femhörningar	150	60	37.616 650	jag	0,982 0114

Vissa definitioner av halvregelbunden polyeder inkluderar ytterligare en figur, den långsträckta kvadratiska gyrobicupolan eller "pseudo-rhombicuboctahedron".

Egenskaper

Antalet hörn är 720° dividerat med vertexvinkeldefekten .

Kuboktaedern och icosidodekaedern är kantlikformiga och kallas kvasi-regelbundna .

Dualerna av arkimedeiska fasta ämnen kallas de katalanska fasta ämnen . Tillsammans med bipyramiderna och trapezoedrarna är dessa ansiktslikformiga fasta ämnen med regelbundna hörn.

Chiralitet

Den snubbade kuben och snubbdodekaedern är kända som chiral , eftersom de kommer i en vänsterhänt form (latin: levomorph eller laevomorph) och högerhänt form (latin: dextromorph). När något kommer i flera former som är varandras tredimensionella spegelbild , kan dessa former kallas för enantiomorfer. (Denna nomenklatur används också för former av vissa kemiska föreningar .)

Konstruktion av arkimedeiska fasta ämnen

Ytterligare information: Uniform polyhedron och Conway polyhedron notation

Arkimedeiska fasta ämnen kan konstrueras som generatorpositioner i ett kalejdoskop .

De olika arkimediska och platoniska fasta ämnena kan relateras till varandra med hjälp av en handfull allmänna konstruktioner. Börjar med en platonsk solid, trunkering innebär att man skär bort hörn. För att bevara symmetri är snittet i ett plan vinkelrätt mot linjen som förenar ett hörn till mitten av polyedern och är densamma för alla hörn. Beroende på hur mycket som är trunkerat (se tabellen nedan) kan olika platoniska och arkimediska (och andra) fasta ämnen skapas. Om trunkeringen är exakt tillräckligt djup så att varje par av ytor från intilliggande hörn delar exakt en punkt, är det känt som en rättelse. En expansion , eller cantellation , innebär att flytta varje vända bort från mitten (med samma avstånd för att bevara symmetrin hos det platonska solida) och ta det konvexa skrovet. Expansion med vridning innebär också att ytorna roteras, och på så sätt delas varje rektangel som motsvarar en kant i två trianglar med en av rektangelns diagonaler. Den sista konstruktionen vi använder här är trunkering av både hörn och kanter. Om man bortser från skalning kan expansion också ses som rättelse av rättelse. Likaså kan avkortningen ses som trunkeringen av rättelse.

Konstruktion av arkimedeiska fasta ämnen

Symmetri		Tetraedrisk	Octaedral		Icosahedral
Startar fast drift	Symbol {p,q}	Tetraeder {3,3}	Kub {4,3}	Oktaeder {3,4}	Dodekaeder {5,3}	Icosahedron {3,5}
Trunkering (t)	t{p,q}	stympad tetraeder	stympad kub	stympad oktaeder	stympad dodekaeder	stympad icosahedron
Rättelse (r) Ambo (a)	r{p,q}	tetratetraeder (oktaeder)	kuboktaeder		icosidodecahedron
Bitruncation (2t) Dual kis (dk)	2t{p,q}	stympad tetraeder	stympad oktaeder	stympad kub	stympad icosahedron	stympad dodekaeder
Birectification (2r) Dual (d)	2r{p,q}	tetraeder	oktaeder	kub	icosahedron	dodekaeder
kantellation (rr) Expansion (e)	rr{p,q}	rhombitetratetrahedron (kuboktaeder)	rhombicuboctahedron		rhombicosidodecahedron
Snub rättad (sr) Snub (s)	sr{p,q}	snub tetratetrahedron (icosahedron)	snubbig kuboktaeder		snubbig icosidodecahedron
Cantitruncation (tr) Fasning (b)	tr{p,q}	trunkerad tetratetraeder (stympad oktaeder)	stympad cuboctahedron		stympad icosidodecahedron

Lägg märke till dualiteten mellan kuben och oktaedern och mellan dodekaedern och ikosaedern. Också, delvis på grund av att tetraedern är självdual, bara en arkimedisk fast substans som som mest har tetraedrisk symmetri. (Alla platoniska fasta ämnen har åtminstone tetraedrisk symmetri, eftersom tetraedrisk symmetri är en symmetrioperation av (dvs. ingår i) oktaedriska och isoedriska symmetrier, vilket visas av det faktum att en oktaeder kan ses som en rätad tetraeder, och en ikosaeder kan användas som en snubbig tetraeder.)

Stereografisk projektion

stympad tetraeder		stympad kub		stympad oktaeder		stympad dodekaeder		stympad icosahedron
triangelcentrerad _	hexagon -centrerad	oktagoncentrerad _	triangelcentrerad _	kvadratiskt centrerad	hexagon -centrerad	Dekagon -centrerad	Triangelcentrerad _	femhörning -centrerad	hexagon -centrerad

kuboktaeder			icosidodecahedron		rhombicuboctahedron			rhombicosidodecahedron
kvadratiskt centrerad	triangelcentrerad _	vertex -centrerad	femhörning -centrerad	triangelcentrerad _	kvadratiskt centrerad	kvadratiskt centrerad	triangelcentrerad _	Pentagon -centrerad	Triangelcentrerad _	Fyrkantigt centrerad

stympad cuboctahedron			stympad icosidodecahedron			snubb kub
kvadratiskt centrerad	hexagon -centrerad	oktagoncentrerad _	dekagon -centrerad	hexagon -centrerad	kvadratiskt centrerad	kvadratiskt centrerad

Se även

• Aperiodisk plattsättning
• Arkimedeansk graf
• Icosaedriska tvillingar
• Lista över enhetliga polyedrar
• Prins Ruperts kub#Generaliseringar
• Kvasikristall
• Vanlig polyeder
• Halvregelbunden polyeder
• Toroidformad polyeder
• Uniform polyeder

Citat

Anförda verk

•   Grünbaum, Branko (2009), "An enduring error", Elemente der Mathematik , 64 (3): 89–101, doi : 10.4171/EM/120 , MR 2520469 . Omtryckt i Pitici, Mircea, ed. (2011), The Best Writing on Mathematics 2010 , Princeton University Press, s. 18–31 .
• Malkevitch, Joseph (1988), "Milestones in the history of polyhedra", i Senechal, M. ; Fleck, G. (red.), Shaping Space: A Polyhedral Approach , Boston: Birkhäuser, s. 80–92 .

Allmänna referenser

•   Jayatilake, Udaya (mars 2005). "Beräkningar på ansikte och vertex regelbundna polyedrar". Matematisk tidning . 89 (514): 76–81. doi : 10.1017/S0025557200176818 . S2CID 125675814 . .
•   Pugh, Anthony (1976). Polyhedra: Ett visuellt tillvägagångssätt . Kalifornien: University of California Press Berkeley. ISBN 0-520-03056-7 . kapitel 2
•   Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design . Dover Publications, Inc. ISBN 0-486-23729-X . (3–9 §)
•    Schreiber, Peter; Fischer, Gisela; Sternath, Maria Luise (2008). "Nytt ljus på återupptäckten av arkimedeiska fasta ämnen under renässansen". Arkiv för Exakta Vetenskapshistoria . 62 (4): 457–467. Bibcode : 2008AHES...62..457S . doi : 10.1007/s00407-008-0024-z . ISSN 0003-9519 . S2CID 122216140 . .

externa länkar

• Weisstein, Eric W. "Archimedean solid" . MathWorld .
• Archimedean Solids av Eric W. Weisstein , Wolfram Demonstrations Project .
• Pappersmodeller av arkimedeiska fasta och katalanska fasta ämnen
• Gratis pappersmodeller (nät) av arkimedeiska fasta ämnen
• The Uniform Polyhedra av Dr R. Mäder
• Archimedean Solids at Visual Polyhedra av David I. McCooey
• Virtual Reality Polyhedra , The Encyclopedia of Polyhedra av George W. Hart
• Näst sista Modular Origami av James S. Plank
• Interaktiva 3D-polyedrar i Java
• Solid Body Viewer är en interaktiv 3D polyhedron viewer som låter dig spara modellen i svg-, stl- eller obj-format.
• Stella: Polyhedron Navigator : Programvara som används för att skapa många av bilderna på den här sidan.
• Pappersmodeller av arkimediska (och andra) polyedrar