Johnson solid

Den långsträckta fyrkantiga gyrobicupolan ( J 37 ), en fast Johnson
Detta 24 liksidiga triangelexempel är inte ett Johnson solid eftersom det inte är konvext.
Detta 24 kvadratiska exempel är inte ett Johnson solid eftersom det inte är strikt konvext (har 180° dihedriska vinklar .)

I geometri är en Johnson solid en strikt konvex polyeder vars varje sida är en vanlig polygon . Det finns inget krav på att varje yta måste vara samma polygon, eller att samma polygoner förenas runt varje vertex . Ett exempel på en Johnson solid är den kvadratbaserade pyramiden med liksidiga sidor ( J 1 ); den har 1 kvadratisk yta och 4 triangulära sidor. Vissa författare kräver att det solida inte är enhetligt (dvs. inte platoniskt fast , arkimediskt fast , enhetligt prisma eller enhetligt antiprisma ) innan de hänvisar till det som ett "Johnson solid".

Som i alla strikt konvexa kroppar möts minst tre ytor vid varje vertex, och summan av deras vinklar är mindre än 360 grader. Eftersom en vanlig polygon har vinklar på minst 60 grader, följer det att högst fem ytor möts vid vilken vertex som helst. Den femkantiga pyramiden ( J ​​2 ) är ett exempel som har en vertex på 5 grader.

Även om det inte finns någon uppenbar begränsning att en given vanlig polygon inte kan vara en yta av ett Johnson-fast ämne, visar det sig att sidorna av Johnson-fasta ämnen som inte är enhetliga (dvs. inte ett platoniskt fast material , arkimediskt fast material , enhetligt prisma eller enhetligt antiprisma ) har alltid 3, 4, 5, 6, 8 eller 10 sidor.

1966 publicerade Norman Johnson en lista som inkluderade alla 92 Johnson-fasta ämnen (exklusive de 5 platoniska fasta kropparna, de 13 arkimediska fasta kropparna, de oändligt många enhetliga prismorna och de oändligt många enhetliga antiprismorna), och gav dem deras namn och nummer. Han bevisade inte att det bara fanns 92, men han gissade att det inte fanns några andra. Victor Zalgaller 1969 bevisade att Johnsons lista var komplett.

Av Johnson solids är den långsträckta kvadratiska gyrobicupolan ( J ​​37 ), även kallad pseudorhombicuboctahedron, unik genom att vara lokalt vertex-likformig: det finns 4 ytor vid varje vertex, och deras arrangemang är alltid detsamma: 3 kvadrater och 1 triangel. Det är dock inte vertextransitivt , eftersom det har olika isometri vid olika hörn, vilket gör det till ett Johnson-fast ämne snarare än ett arkimediskt fast ämne .

Namn

Namnet på Johnson solids följer en flexibel och exakt beskrivande formel, så att många fasta ämnen kan namnges på olika sätt utan att kompromissa med deras noggrannhet som beskrivning. De flesta fasta ämnen från Johnson kan konstrueras från de första ( pyramider , kupoler och rotundor ), tillsammans med de platoniska och arkimediska soliderna, prismorna och antiprismorna ; mitten av ett visst fast ämnes namn kommer att återspegla dessa ingredienser. Därifrån är en serie prefix kopplade till ordet för att indikera tillägg, rotationer och transformationer:

  • Bi-[<>] indikerar att två kopior av det fasta ämnet i fråga är sammanfogade bas-till-bas. För kupoler och rotundor kan de fasta ämnena sammanfogas så att antingen lika ytor ( orto- ) eller olika ytor ( gyro-[*] ) möts. Med hjälp av denna nomenklatur kan en oktaeder beskrivas som en kvadratisk bipyramid[4<>] , en kuboktaeder som en triangulär gyrobicupola[3cc*] och en icosidodecahedron som en femkantig gyrobirotunda[5rr*] .
  • Långsträckt[=] indikerar att ett prisma är förbundet med basen av det fasta ämnet i fråga, eller mellan baserna i fallet med Bi-fasta ämnen. En rhombicuboctahedron kan alltså beskrivas som en långsträckt fyrkantig ortobicupola .
  • Gyroförlängd[z] indikerar att ett antiprisma är förbundet med basen av det fasta ämnet i fråga eller mellan baserna när det gäller Bi-fasta ämnen. En ikosaeder kan alltså beskrivas som en gyroförlängd femkantig bipyramid .
  • Augmented[+] indikerar att en annan polyeder, nämligen en pyramid eller kupol , är förenad med en eller flera ytor av det fasta ämnet i fråga.
  • Förminskad[-] indikerar att en pyramid eller kupol har tagits bort från en eller flera ytor av det fasta ämnet i fråga.
  • Gyrat [*] indikerar att en kupol som är monterad på eller förekommer i det aktuella fasta materialet roteras så att olika kanter matchar varandra, som i skillnaden mellan orto- och gyrobicupolae.

De tre sista operationerna – förstärkning , förminskning och svängning – kan utföras flera gånger för vissa stora fasta ämnen. Bi- & Tri- indikerar en dubbel respektive trippel operation. Till exempel har en bigyratfast substans två roterade kupoler, och en treförminskad fast substans har tre borttagna pyramider eller kupoler.

I vissa stora fasta ämnen skiljer man mellan fasta ämnen där ändrade ytor är parallella och fasta ämnen där ändrade ytor är sneda. Para- indikerar det förra, att det fasta ämnet i fråga har förändrade parallella ytor, och meta- det senare, ändrade sneda ytor. Till exempel har en parabiaförstärkt fast substans fått två parallella ytor förstärkta, och en metabigyrat solid har fått två snedställda ytor gyrerade.

De sista Johnson-fastämnena har namn baserade på vissa polygonkomplex från vilka de är sammansatta. Dessa namn definieras av Johnson med följande nomenklatur:

  • En lune är ett komplex av två trianglar fästa på motsatta sidor av en kvadrat.
  • Spheno - indikerar ett killiknande komplex som bildas av två intilliggande lunes. Dispheno- indikerar två sådana komplex.
  • Hebespheno - indikerar ett trubbigt komplex av två luner åtskilda av en tredje lune.
  • Corona är ett kronliknande komplex av åtta trianglar.
  • Megacorona är ett större kronliknande komplex av 12 trianglar.
  • Suffixet - cingulum indikerar ett bälte med 12 trianglar.

Uppräkning

Ytterligare information: Lista över Johnsons fasta ämnen

Pyramider, kupoler och rotunda

De första 6 Johnson soliderna är pyramider, kupoler eller rotundor med högst 5 sidoytor. Pyramider och kupoler med 6 eller fler sidoytor är i samma plan och är därför inte Johnson-fasta ämnen.

Pyramider

De två första Johnson-fastämnena, J1 och J2, är pyramider . Den triangulära pyramiden är den regelbundna tetraedern , så det är inte ett Johnson-fast ämne. De representerar delar av vanliga polyedrar.

Vanlig 3> T J14> J2 5>

Triangulär pyramid ( tetraeder ) 		Fyrkantig pyramid Pentagonal pyramid
Tetrahedron.png Square pyramid.png Pentagonal pyramid.png
Tetrahedron flat.svg Johnson solid 1 net.png Johnson solid 2 net.png
Besläktade regelbundna polyedrar
Tetraeder Oktaeder Icosahedron
Tetrahedron.png Octahedron.png Icosahedron.png

Kupoler och rotunda

De nästa fyra Johnson soliderna är tre kupoler och en rotunda . De representerar sektioner av enhetliga polyedrar.

Kupol Rotunda
Enhetlig J3 3c aC- J4 4c J5 5c J6 5r aD-


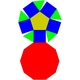
Fastigium (Digonal kupol) ( triangulärt prisma ) 		Trekantig kupol Fyrkantig kupol Femkantig kupol Femkantig rotunda
Triangular prism wedge.png Triangular cupola.png Square cupola.png Pentagonal cupola.png Pentagonal rotunda.png
Johnson solid 3 net.png Johnson solid 4 net.png Johnson solid 5 net.png Johnson solid 6 net.png
Besläktade enhetliga polyedrar
Cuboctahedron Rhombicuboctahedron Rhombicosidodecahedron Icosidodecahedron
Cuboctahedron.png Small rhombicuboctahedron.png Small rhombicosidodecahedron.png Icosidodecahedron.png

Modifierade pyramider

Johnsons fasta ämnen 7 till 17 härrör från pyramider.

Avlånga och gyrolånga pyramider

I den gyrolånga triangulära pyramiden är tre par av intilliggande trianglar i samma plan och bildar icke-kvadratrombi, så det är inte ett Johnson-fast ämne.

Avlånga pyramider Gyrolånga pyramider
J7 3=> J8 4=> J9 5=> Coplanar J10 4z> J11 5z> I-
Långsträckt triangulär pyramid Långsträckt fyrkantig pyramid Långsträckt femkantig pyramid
Gyroförlängd triangulär pyramid ( förminskad trigonal trapezhedron ) 		Gyroelång fyrkantig pyramid Gyrolånga femkantiga pyramid
Elongated triangular pyramid.png Elongated square pyramid.png Elongated pentagonal pyramid.png Augmented octahedron.png Gyroelongated square pyramid.png Gyroelongated pentagonal pyramid.png
Johnson solid 7 net.png Johnson solid 8 net.png Johnson solid 9 net.png Augmented octahedgon net.png Johnson solid 10 net.png Johnson solid 11 net.png
Förstärkt från polyedrar

tetrahedron triangulärt prisma
fyrkantig pyramidkub
pentagonal pyramid femkantig prisma
tetraeder oktaeder
fyrkantig pyramid fyrkantig antiprisma
pentagonal pyramid femkantig antiprisma
Tetrahedron.png Triangular prism.png Square pyramid.png Hexahedron.png Pentagonal pyramid.png Pentagonal prism.png Tetrahedron.png Octahedron.png Square pyramid.png Square antiprism.png Pentagonal pyramid.png Pentagonal antiprism.png

Bipyramider

Den fyrkantiga bipyramiden är den regelbundna oktaedern , medan den gyrolånga femkantiga bipyramiden är den vanliga ikosaedern , så de är inte Johnson-fasta ämnen. I den gyrolånga triangulära bipyramiden är sex par av intilliggande trianglar i samma plan och bildar icke-fyrkantiga rombi, så det är inte heller ett Johnson-fast ämne.

Bipyramider Avlånga bipyramider Gyrolånga bipyramider
J12 3<> Regelbunden J13 5<> J14 3<=> J15 4<=> J16 5<=> Coplanar J17 4<z> Regelbunden
Triangulär bipyramid
Fyrkantig bipyramid ( oktaeder ) 		Pentagonal bipyramid Långsträckt triangulär bipyramid Långsträckt fyrkantig bipyramid Långsträckt femkantig bipyramid
Gyrolängd triangulär bipyramid ( trigonal trapetsoeder ) 		Gyroelång fyrkantig bipyramid
Gyrolånga femkantiga bipyramid ( ikosaeder )
Triangular dipyramid.png Octahedron.png Pentagonal dipyramid.png Elongated triangular dipyramid.png Elongated square dipyramid.png Elongated pentagonal dipyramid.png Gyroelongated triangular bipyramid.png Gyroelongated square dipyramid.png Pentagonal gyroelongated bipyramid.png
Johnson solid 12 net.png Octahedron flat.svg Johnson solid 13 net.png Johnson solid 14 net.png Johnson solid 15 net.png Johnson solid 16 net.png Johnson solid 17 net.png Icosahedron flat.svg
Förstärkt från polyedrar
tetraeder fyrkantig pyramid femkantig pyramid
tetrahedron triangulärt prisma
fyrkantig pyramidkub
pentagonal pyramid femkantig prisma
tetraeder Oktaeder
fyrkantig pyramid fyrkantig antiprisma
pentagonal pyramid femkantig antiprisma
Tetrahedron.png Square pyramid.png Pentagonal pyramid.png Tetrahedron.png Triangular prism.png Square pyramid.png Hexahedron.png Pentagonal pyramid.png Pentagonal prism.png Tetrahedron.png Octahedron.png Square pyramid.png Square antiprism.png Pentagonal pyramid.png Pentagonal antiprism.png

Modifierade kupoler och rotundor

Johnson fasta ämnen 18 till 48 härrör från kupoler och rotundor.

Avlånga och gyrolånga kupoler och rotundor

Avlång kupol Långsträckt rotunda Gyroelång kupol Gyrolånga rotunda
Coplanar J18 3c= J19 4c= eC- J205c= J21 5r= Konkav J22 3cz J23 4cz J24 5cz J25 5rz
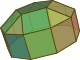
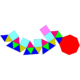
Förlängt fastigium Långsträckt triangulär kupol Långsträckt fyrkantig kupol Långsträckt femkantig kupol Långsträckt femkantig rotunda Gyrolångt fastigium Gyroelång triangulär kupol Gyroelång fyrkantig kupol Gyrolång femkantig kupol Gyrolånga femkantiga rotunda
Elongated digonal cupola.png Elongated triangular cupola.png Elongated square cupola.png Elongated pentagonal cupola.svg Elongated pentagonal rotunda.png Gyroelongated digonal cupola.png Gyroelongated triangular cupola.png Gyroelongated square cupola.png Gyroelongated pentagonal cupola.png Gyroelongated pentagonal rotunda.png
Johnson solid 18 net.png Johnson solid 19 net.png Johnson solid 20 net.png Johnson solid 21 net.png Johnson solid 22 net.png Johnson solid 23 net.png Johnson solid 24 net.png Johnson solid 25 net.png
Förstärkt från polyedrar

Fyrkantigt prisma Triangulärt prisma
Sexkantigt prisma Triangulär kupol
Åttakantigt prisma Fyrkantig kupol
Dekagonalt prisma Femkantig kupol
Dekagonalt prisma Pentagonal rotunda
kvadratiskt antiprisma Triangulärt prisma
Hexagonal antiprisma Triangulär kupol
Åttakantig antiprisma Fyrkantig kupol
Dekagonal antiprisma Femkantig kupol
Dekagonal antiprisma Pentagonal rotunda
Tetragonal prism.png Triangular prism.png Hexagonal prism.png Triangular cupola.png Octagonal prism.png Square cupola.png Decagonal prism.png Pentagonal cupola.png Decagonal prism.png Pentagonal rotunda.png Square antiprism.png Triangular prism.png Hexagonal antiprism.png Triangular cupola.png Octagonal antiprism.png Square cupola.png Decagonal antiprism.png Pentagonal cupola.png Decagonal antiprism.png Pentagonal rotunda.png

Bicupolae

Den triangulära gyrobicupolan är en arkimedisk fast substans (i det här fallet kuboktaedern ), så det är inte ett Johnson-fast ämne.

Ortobicupola Gyrobicupola
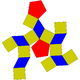
Coplanar J27 3cc J28 4cc J30 5cc J26 2cc* Halvregelbunden J29 4cc* J31 5cc*
Orthobifastigium Triangulär ortobicupola Fyrkantig ortobikupa Pentagonal ortobicupola Gyrobifastigium
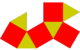
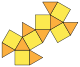
Triangulär gyrobicupola ( kuboktaeder ) 		Fyrkantig gyrobicupola Pentagonal gyrobicupola
Digonal orthobicupola.png Triangular orthobicupola.png Square orthobicupola.png Pentagonal orthobicupola.png Gyrobifastigium.png Cuboctahedron.png Square gyrobicupola.png Pentagonal gyrobicupola.png
Johnson solid 27 net.png Johnson solid 28 net.png Johnson solid 30 net.png Johnson solid 26 net.png Cuboctahedron flat.svg Johnson solid 29 net.png Johnson solid 31 net.png
Förstärkt från polyeder
Trekantsprisma Trekantig kupol Fyrkantig kupol Femkantig kupol Trekantsprisma Trekantig kupol Fyrkantig kupol Femkantig kupol
Triangular prism.png Triangular cupola.png Square cupola.png Pentagonal cupola.png Triangular prism.png Triangular cupola.png Square cupola.png Pentagonal cupola.png

Kupolrotunda och birotunda

Den femkantiga gyrobirotundan är ett arkimedisk fast ämne (i det här fallet icosidodecahedron ), så det är inte ett Johnson-fast ämne.

Kupol-rotunda Birotunda
J32 5kr J33 5cr* J34 5rr ad* Halvregelbunden
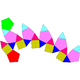
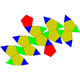
Pentagonal ortocupolarotunda Pentagonal gyrocupolarotunda Pentagonal ortobirotunda
Pentagonal gyrobirotunda ( icosidodecahedron )
Pentagonal orthocupolarotunda.png Pentagonal gyrocupolarotunda.png Pentagonal orthobirotunda.png Icosidodecahedron.png
Johnson solid 32 net.png Johnson solid 33 net.png Johnson solid 34 net.png Icosidodecahedron flat.svg
Förstärkt från polyedrar

Femkantig kupol Femkantig rotunda 		Femkantig rotunda
Pentagonal cupola.png Pentagonal rotunda.png Pentagonal rotunda.png

Långsträckta bikupoler

Den långsträckta fyrkantiga ortobikupan är en arkimedisk fast substans (i det här fallet rhombicuboctahedron ), så det är inte ett Johnson-fast ämne.

Långsträckt ortobikupa Långsträckt gyrobicupola
Coplanar J35 3c=c Halvregelbunden J38 5c=c Coplanar J36 3c=c* J37 4c=c* eC* J39 5c=c*
Långsträckt ortobifastigium Långsträckt triangulär ortobikupa
Långsträckt fyrkantig ortobicupola ( rhombicuboctahedron ) 		Långsträckt femkantig ortobikupa Avlångt gyrobifastigium Långsträckt triangulär gyrobicupola Långsträckt fyrkantig gyrobicupola Långsträckt femkantig gyrobicupola
Elongated digonal orthobicupola.png Elongated triangular orthobicupola.png Small rhombicuboctahedron.png Elongated pentagonal orthobicupola.png Elongated digonal gyrobicupola.png Elongated triangular gyrobicupola.png Elongated square gyrobicupola.png Elongated pentagonal gyrobicupola.png
Johnson solid 35 net.png Rhombicuboctahedron flat.png Johnson solid 38 net.png Johnson solid 36 net.png Johnson solid 37 net.png Johnson solid 39 net.png
Förstärkt från polyedrar

Fyrkantigt prisma Triangulärt prisma
Sexkantigt prisma Triangulär kupol
Åttakantigt prisma Fyrkantig kupol
Dekagonalt prisma Femkantig kupol
Fyrkantigt prisma Triangulärt prisma
Sexkantigt prisma Triangulär kupol
Åttakantigt prisma Fyrkantig kupol
Dekagonalt prisma Femkantig kupol
Tetragonal prism.png Triangular prism.png Hexagonal prism.png Triangular cupola.png Octagonal prism.png Square cupola.png Decagonal prism.png Pentagonal cupola.png Tetragonal prism.png Triangular prism.png Hexagonal prism.png Triangular cupola.png Octagonal prism.png Square cupola.png Decagonal prism.png Pentagonal cupola.png

Långsträckta kupolrotunda och birotunda

Långsträckt kupol-rotunda Långsträckt birotunda
J40 5c=r J41 5c=r* J42 5r=r J43 5r=r*
Långsträckt femkantig ortocupolarotunda Långsträckt femkantig gyrocupolarotunda Långsträckt femkantig ortobirotunda Långsträckt femkantig gyrobirotunda
Elongated pentagonal orthocupolarotunda.png Elongated pentagonal gyrocupolarotunda.png Elongated pentagonal orthobirotunda.png Elongated pentagonal gyrobirotunda.png
Johnson solid 40 net.png Johnson solid 41 net.png Johnson solid 42 net.png Johnson solid 43 net.png
Förstärkt från polyedrar


Decagonal prisma Femkantig kupol Femkantig rotunda
Dekagonalt prisma Pentagonal rotunda
Decagonal prism.png Pentagonal cupola.png Pentagonal rotunda.png Decagonal prism.png Pentagonal rotunda.png

Gyrolånga bicupolae, cupola-rotundas och birotundas

Dessa fasta ämnen från Johnson har 2 kirala former.

Gyroelång bikupa Gyrolånga kupol-rotunda Gyrolånga birotunda
Konkav J44 3czc J45 4czc J46 5czc J47 5czr J48 5rzr
Gyrolångt bifastigium Gyroelång triangulär bikupa Gyroelång fyrkantig bikupa Gyroelång femkantig bikupa Gyrolånga femkantiga kupolrotunda Gyrolånga femkantiga birotunda
Gyroelongated digonal bicupola.png Gyroelongated triangular bicupola.png Gyroelongated square bicupola.png Gyroelongated pentagonal bicupola.png Gyroelongated pentagonal cupolarotunda.png Gyroelongated pentagonal birotunda.png
Johnson solid 44 net.png Johnson solid 45 net.png Johnson solid 46 net.png Johnson solid 47 net.png Johnson solid 48 net.png
Förstärkt från polyedrar

Triangulärt prisma Fyrkantigt antiprisma
Triangulär kupol Hexagonal antiprisma
Fyrkantig kupol Åtkantig antiprisma
Femkantig kupol Dekagonal antiprisma

Femkantig kupol Femkantig rotunda Dekagonal antiprisma
Femkantig rotunda Dekagonal antiprisma
Triangular prism.png Square antiprism.png Triangular cupola.png Hexagonal antiprism.png Square cupola.png Octagonal antiprism.png Pentagonal cupola.png Decagonal antiprism.png Pentagonal cupola.png Pentagonal rotunda.png Decagonal antiprism.png Pentagonal rotunda.png Decagonal antiprism.png

Förstärkta prismor

Johnson solids 49 till 57 är byggda genom att förstärka sidorna av prismor med fyrkantiga pyramider.

Förstärkta triangulära prismor Förstärkta femkantiga prismor Förstärkta hexagonala prismor
J49 3=+ J503=++ J51 3=+++ J52 5=+ J53 5=++ J54 6=+ J55 6=++ J56 6=+x J57 6=+++
Förstärkt triangulärt prisma Biaugmenterat triangulärt prisma Triaugmenterat triangulärt prisma Förstärkt femkantigt prisma Biaugmented pentagonal prisma Förstärkt hexagonalt prisma Parabiaförstärkt hexagonalt prisma Metabiaförstärkt hexagonalt prisma Triaugmenterat hexagonalt prisma
Augmented triangular prism.png Biaugmented triangular prism.png Triaugmented triangular prism.png Augmented pentagonal prism.png Biaugmented pentagonal prism.png Augmented hexagonal prism.png Parabiaugmented hexagonal prism.png Metabiaugmented hexagonal prism.png Triaugmented hexagonal prism.png
Johnson solid 49 net.png Johnson solid 50 net.png Johnson solid 51 net.png Johnson solid 52 net.png Johnson solid 53 net.png Johnson solid 54 net.png Johnson solid 55 net.png Johnson solid 56 net.png Johnson solid 57 net.png
Förstärkt från polyedrar

Triangulärt prisma Fyrkantig pyramid
Femkantigt prisma Fyrkantig pyramid
Sexkantigt prisma Fyrkantig pyramid
Triangular prism.png Square pyramid.png Pentagonal prism.png Square pyramid.png Hexagonal prism.png Square pyramid.png

J8 och J15 skulle också passa här, som ett förstärkt kvadratiskt prisma och ett dubbelförstärkt kvadratiskt prisma.

Modifierade platonska fasta ämnen

Johnson solids 58 till 64 är byggda genom att förstärka eller förminska platoniska solids.

Förstärkta dodekaedrar

J58 D+ J59 D++ J60 D+x J61 D+++
Förstärkt dodekaeder Parabiaugmented dodecahedron Metabiaförstärkt dodekaeder Triaugmenterad dodekaeder
Augmented dodecahedron.png Parabiaugmented dodecahedron.png Metabiaugmented dodecahedron.png Triaugmented dodecahedron.png
Johnson solid 58 net.png Johnson solid 59 net.png Johnson solid 60 net.png Johnson solid 61 net.png
Förstärkt från polyeder
Dodecahedron och femkantig pyramid
Dodecahedron.png Pentagonal pyramid.png

Förminskad och förstärkt förminskad icosahedra

Förminskad icosahedron Förstärkt treförminskad icosahedron

J11 (upprepad) 		Enhetlig J62 I-/ J63 I--- J64 I---+

Förminskad icosahedron ( gyroförlängd femkantig pyramid )
Parabidiminished icosahedron ( Pentagonal antiprism ) 		Metabidiminiserad icosahedron Treförminskad icosahedron Förstärkt treförminskad icosahedron
Gyroelongated pentagonal pyramid.png Pentagonal antiprism.png Metabidiminished icosahedron.png Tridiminished icosahedron.png Augmented tridiminished icosahedron.png
Johnson solid 11 net.png Johnson solid 62 net.png Johnson solid 63 net.png Johnson solid 64 net.png

Modifierade arkimediska fasta ämnen

Johnson solids 65 till 83 är byggda genom att förstärka, förminska eller rotera arkimedeiska fasta ämnen.

Förstärkta arkimedeiska fasta ämnen

Förstärkt trunkerad tetraeder Förstärkta trunkerade kuber Förstärkta trunkerade dodekaedrar
J65 tT+ J66 tC+ J67 tC++ J68 tD+ J69 tD++ J70 tD+x J71 tD+++
Förstärkt trunkerad tetraeder Förstärkt trunkerad kub Biaugmented trunkerad kub Förstärkt stympad dodekaeder Parabiaugmented trunkerad dodekaeder Metabiaförstärkt trunkerad dodekaeder Triaugmenterad trunkerad dodekaeder
Augmented truncated tetrahedron.png Augmented truncated cube.png Biaugmented truncated cube.png Augmented truncated dodecahedron.png Parabiaugmented truncated dodecahedron.png Metabiaugmented truncated dodecahedron.png Triaugmented truncated dodecahedron.png
Johnson solid 65 net.png Johnson solid 66 net.png Johnson solid 67 net.png Johnson solid 68 net.png Johnson solid 69 net.png Johnson solid 70 net.png Johnson solid 71 net.png
Förstärkt från polyedrar

stympad tetraeder triangulär kupol
stympad kub fyrkantig kupol
stympad dodekaeder femkantig kupol
Truncated tetrahedron.png Triangular cupola.png Truncated hexahedron.png Square cupola.png Truncated dodecahedron.png Pentagonal cupola.png

Gyrat och förminskad rhombicosidodecahedra

Gyrat rhombicosidodecahedra
J72 eD* J73 eD** J74 eD*' J75 eD***
Gyrat rhombicosidodecahedron Parabigyrat rhombicosidodecahedron Metabigyrat rhombicosidodecahedron Trigyrat rhombicosidodecahedron
Gyrate rhombicosidodecahedron.png Parabigyrate rhombicosidodecahedron.png Metabigyrate rhombicosidodecahedron.png Trigyrate rhombicosidodecahedron.png
Johnson solid 72 net.png Johnson solid 73 net.png Johnson solid 74 net.png Johnson solid 75 net.png
Förminskad rhombicosidodecahedra
J76 eD- J80 eD-- J81 eD-/ J83 eD---
Förminskad rhombicosidodecahedron Parabidförminskad rhombicosidodecahedron Metabidiminiserad rhombicosidodecahedron Treförminskad rhombicosidodecahedron
Diminished rhombicosidodecahedron.png Parabidiminished rhombicosidodecahedron.png Metabidiminished rhombicosidodecahedron.png Tridiminished rhombicosidodecahedron.png
Johnson solid 76 net.png Johnson solid 80 net.png Johnson solid 81 net.png Johnson solid 83 net.png
Gyrat förminskad rhombicosidodecahedra
J77 -* J78 -' J79 -** J82 --*
Paragyrat förminskad rhombicosidodecahedron Metagyrat minskad rhombicosidodecahedron Bigyrate förminskad rhombicosidodecahedron Gyrat dubbelförminskad rhombicosidodecahedron
Paragyrate diminished rhombicosidodecahedron.png Metagyrate diminished rhombicosidodecahedron.png Bigyrate diminished rhombicosidodecahedron.png Gyrate bidiminished rhombicosidodecahedron.png
Johnson solid 77 net.png Johnson solid 78 net.png Johnson solid 79 net.png Johnson solid 82 net.png

J37 skulle också visas här som en duplikat (det är en gyrat rhombicuboctahedron).

Andra gyrater och minskade arkimediska fasta ämnen

Andra arkimediska fasta ämnen kan roteras och förminskas, men de resulterar alla i tidigare räknade fasta ämnen.

J27 J 3 J34 J6 J37 J19 Enhetlig

Gyrate cuboctahedron ( triangulär ortobicupola )
Förminskad cuboctahedron ( triangulär kupol )
Gyrate icosidodecahedron ( femkantig orthobirotunda )
Förminskad icosidodecahedron ( femkantig rotunda )
Gyrat rhombicuboctahedron ( långsträckt fyrkantig gyrobicupola )
Förminskad rhombicuboctahedron ( långsträckt fyrkantig kupol )
Dubbelförminskad rhombicuboctahedron ( åttkantigt prisma )
Triangular orthobicupola.png Triangular cupola.png Pentagonal orthobirotunda.png Pentagonal rotunda.png Elongated square gyrobicupola.png Elongated square cupola.png Octagonal prism.png
Johnson solid 27 net.png Johnson solid 3 net.png Johnson solid 34 net.png Johnson solid 6 net.png Johnson solid 37 net.png Johnson solid 19 net.png
Gyrerad eller förminskad från polyedrar
Cuboctahedron Icosidodecahedron Rhombicuboctahedron
Cuboctahedron.png Icosidodecahedron.png Small rhombicuboctahedron.png

Elementära fasta ämnen

Johnsons fasta ämnen 84 till 92 är inte härledda från "klipp-och-klistra"-manipulationer av enhetliga fasta ämnen.

Snubbade antiprismor

De snubbade antiprismorna kan konstrueras som en alternering av en trunkerad antiprisma. Gyrobianticupolae är en annan konstruktion för de snubbade antiprismorna. Endast snubbade antiprismor med högst 4 sidor kan konstrueras av vanliga polygoner. Den snubbiga triangulära antiprisman är den vanliga icosahedronen , så det är inte en Johnson solid.

J84 Regelbunden J85

Snub disphenoid ss{2,4}
Icosahedron ss{2,6}
Snub square antiprism ss{2,8}
Digonal gyrobianticupola Triangulär gyrobianticupola Fyrkantig gyrobianticupola
Snub digonal antiprism.png Snub triangular antiprism.png Snub square antiprism colored.png
Snub disphenoid net snubcoloring.png Snub triangular antiprism net.png Snub square antiprism net snubcoloring.png

Andra

J86 J87 J88
Sphenocorona Förstärkt sphenocorona Sphenomegacorona
Sphenocorona.png Augmented sphenocorona.png Sphenomegacorona.png
Johnson solid 86 net.png Johnson solid 87 net.png Johnson solid 88 net.png
J89 J90 J91 J92
Hebesphenomegacorona Disphenocingulum Bilunabirotunda Triangulär hebesphenorotunda
Hebesphenomegacorona.png Disphenocingulum.png Bilunabirotunda.png Triangular hebesphenorotunda.png
Johnson solid 89 net.png Johnson solid 90 net.png Johnson solid 91 net.png Johnson solid 92 net.png

Klassificering efter typer av ansikten

Triangel-faced Johnson solids

Fem Johnson-fasta ämnen är deltaedrar , med alla liksidiga triangelytor:

J12 Triangulär bipyramid Triangular dipyramid.png
J13 Femkantig bipyramid Pentagonal dipyramid.png
J17 Gyrolängd fyrkantig bipyramid Gyroelongated square dipyramid.png
J51 Triaugmenterad triangulär prisma Triaugmented triangular prism.png
J84 Snub disfenoid Snub disphenoid.png

Triangel och fyrkantiga Johnson solids

Tjugofyra Johnson-kroppar har bara triangel- eller fyrkantiga ytor:

J1 Fyrkantig pyramid Square pyramid.png
J7 Långsträckt triangulär pyramid Elongated triangular pyramid.png
J8 Långsträckt fyrkantig pyramid Elongated square pyramid.png
J10 Gyrolängd fyrkantig pyramid Gyroelongated square pyramid.png
J14 Långsträckt triangulär bipyramid Elongated triangular dipyramid.png
J15 Långsträckt fyrkantig bipyramid Elongated square dipyramid.png
J16 Långsträckt femkantig bipyramid Elongated pentagonal dipyramid.png
J26 Gyrobifastigium Gyrobifastigium.png
J27 Triangulär ortobicupola Triangular orthobicupola.png
J28 Fyrkantig ortobicupola Square orthobicupola.png
J29 Fyrkantig gyrobicupola Square gyrobicupola.png
J35 Långsträckt triangulär ortobicupola Elongated triangular orthobicupola.png
J36 Långsträckt triangulär gyrobicupola Elongated triangular gyrobicupola.png
J37 Långsträckt fyrkantig gyrobicupola Elongated square gyrobicupola.png
J44 Gyroelång triangulär bikupa Gyroelongated triangular bicupola.png
J45 Gyrolånga fyrkantig bikupa Gyroelongated square bicupola.png
J49 Förstärkt triangulärt prisma Augmented triangular prism.png
J50 Biaugmenterat triangulärt prisma Biaugmented triangular prism.png
J85 Snub kvadratiskt antiprisma Snub square antiprism.png
J86 Sphenocorona Sphenocorona.png
J87 Augmented sphenocorona Augmented sphenocorona.png
J88 Sphenomegacorona Sphenomegacorona.png
J89 Hebesphenomegacorona Hebesphenomegacorona.png
J90 Disphenocingulum Disphenocingulum.png

Triangel och femkantiga Johnson solids

Elva Johnson solids har bara triangel- och femkantytor:

J2 Pentagonal pyramid Pentagonal pyramid.png
J11 Gyrolongerad femkantig pyramid Gyroelongated pentagonal pyramid.png
J34 Pentagonal ortobirotunda Pentagonal orthobirotunda.png
J48 Gyrolongerad femkantig birotunda Gyroelongated pentagonal birotunda.png
J58 Augmented dodecahedron Augmented dodecahedron.png
J59 Parabiaugmented dodecahedron Parabiaugmented dodecahedron.png
J60 Metabiaugmented dodecahedron Metabiaugmented dodecahedron.png
J61 Triaugmented dodecahedron Triaugmented dodecahedron.png
J62 Metabidiminished icosahedron Metabidiminished icosahedron.png
J63 Trediminished icosahedron Tridiminished icosahedron.png
J64 Augmented triminished icosahedron Augmented tridiminished icosahedron.png

Triangel, fyrkantig och femkantig Johnson solids

Tjugo Johnson solids har bara triangel-, kvadrat- och femkantytor:

J09 Långsträckt femkantig pyramid Elongated pentagonal pyramid.png
J30 Femkantig ortobicupola Pentagonal orthobicupola.png
J31 Femkantig gyrobicupola Pentagonal gyrobicupola.png
J32 Pentagonal ortocupolarotunda Pentagonal orthocupolarotunda.png
J33 Pentagonal gyrocupolarotunda Pentagonal gyrocupolarotunda.png
J38 gyrobicupola Elongated pentagonal orthocupolarotunda.png
Långsträckt femkantig ortobicupola Långsträckt femkantig gyrobicupola Elongated pentagonal gyrobicupola.png
J39 Ellonged pentagonal Elongated pentagonal orthobicupola.png
J4 gyrocupolarotunda Elongated pentagonal gyrocupolarotunda.png
J42 Långsträckt femkantig ortobirotunda Elongated pentagonal orthobirotunda.png
J43 Långsträckt pentagonal gyrobirotunda Elongated pentagonal gyrobirotunda.png
J46 Gyrolongerad femkantig bicupola Gyroelongated pentagonal bicupola.png
J47 Gyrolongerad femkantig cupolarotunda Gyroelongated pentagonal cupolarotunda.png
J52 Augmented pentagonal Augmented pentagonal prism.png
J75 prisma Biaugmented pentagonal prism.png
J53 Gyrate rhombicosidodecahedron Gyrate rhombicosidodecahedron.png
Biaugmented pentagonal prisma J72 Metabigyrate rhombicosidodecahedron.png
J73 Parabicogyrate 4dembicode Parabigyrate rhombicosidodecahedron.png
J91 cahedron Bilunabirotunda.png
Bilunabirotunda Trigyrate rhombicosidodecahedron Trigyrate rhombicosidodecahedron.png

Triangel, fyrkantig och sexkantig Johnson solids

Åtta Johnson-fasta kroppar har bara triangel-, kvadrat- och hexagonytor:

J3 Triangulär kupol Triangular cupola.png
J18 Långsträckt trekantig kupol Elongated triangular cupola.png
J22 Gyroelång trekantig kupol Gyroelongated triangular cupola.png
J54 Förstärkt sexkantigt prisma Augmented hexagonal prism.png
J55 Parabiaugmented hexagonal prisma Parabiaugmented hexagonal prism.png
J56 Metabiaugmented hexagonal prisma Metabiaugmented hexagonal prism.png
J57 Triaugmented hexagonal prisma Triaugmented hexagonal prism.png
J65 Augmented trunkated tetrahedron Augmented truncated tetrahedron.png

Triangel, fyrkantig och åttakantig Johnson solids

Fem Johnson-kroppar har bara triangel-, kvadrat- och oktagonytor:

J4 Fyrkantig kupol Square cupola.png
J19 Avlång fyrkantig kupol Elongated square cupola.png
J23 Gyroelång fyrkantig kupol Gyroelongated square cupola.png
J66 Augmented trunkerad kub Augmented truncated cube.png
J67 Biaugmented trunkerad kub Biaugmented truncated cube.png

Triangel-, pentagon- och dekagon-faced Johnson solids

Två Johnson solids har bara triangel-, femkant- och dekagonytor:

J06 Pentagonal rotunda Pentagonal rotunda.png
J25 Gyrolängd femkantig rotunda Gyroelongated pentagonal rotunda.png

Triangel-, kvadrat-, femhörnings- och hexagon-faced Johnson solids

Endast en Johnson solid har triangel-, kvadrat-, femkant- och hexagonytor:

J92 Triangulär hebesphenorotunda Triangular hebesphenorotunda.png

Triangel-, kvadrat-, femhörnings- och dekagon-faced Johnson solids

Sexton Johnson solids har bara triangel-, kvadrat-, pentagon- och dekagonytor:

J05 Femkantig kupol Pentagonal cupola.png
J20 Förlängd femkantig kupol Elongated pentagonal cupola.svg
J21 Förlängd femkantig rotunda Elongated pentagonal rotunda.png
J24 Gyroförlängd femkantig kupol Gyroelongated pentagonal cupola.png
J68 Augmented trunkerad dodekaeder Augmented truncated dodecahedron.png
J69 Parabiaugmented trunkerad dodekaeder Parabiaugmented truncated dodecahedron.png
J70 Metabiaugmented trunkerad trunkerad dodekaeder Metabiaugmented truncated dodecahedron.png
Trekantig dodekaeder Trekantig dodekaeder Triaugmented truncated dodecahedron.png
J76 Förminskad rhombicosidodecahedron Diminished rhombicosidodecahedron.png
J77 Paragyrat förminskad rhombicosidodecahedron Paragyrate diminished rhombicosidodecahedron.png
J78 Gyrat dubbelförminskad rhombicosidodecahedron Gyrate bidiminished rhombicosidodecahedron.png
Metagyrat förminskad rhombicosidodecahedron Metagyrate diminished rhombicosidodecahedron.png
J79 Bigyrate förminskad rhombicosidodecahedron Bigyrate diminished rhombicosidodecahedron.png
J82 J80 Metabidiminished rhombicosidodecahedron.png
Parabidiminished rhombicosidodecahedron J8sminished rhombicosidocahedr ron Parabidiminished rhombicosidodecahedron.png
J83 Treförminskad rhombicosidodecahedron Tridiminished rhombicosidodecahedron.png

Omskrivbara Johnson fasta ämnen

25 av Johnson-fastämnena har hörn som finns på ytan av en sfär : 1–6,11,19,27,34,37,62,63,72–83. Alla av dem kan ses vara relaterade till en regelbunden eller enhetlig polyedra genom gyration, förminskning eller dissektion.

Oktaeder Cuboctahedron Rhombicuboctahedron
J1
Square pyramid.png 		J 3
Triangular cupola.png 		J27
Triangular orthobicupola.png 		J4
Square cupola.png 		J19
Elongated square cupola.png 		J37
Elongated square gyrobicupola.png
Icosahedron Icosidodecahedron
J2
Pentagonal pyramid.png 		J11
Gyroelongated pentagonal pyramid.png 		J62
Metabidiminished icosahedron.png 		J63
Tridiminished icosahedron.png 		J6
Pentagonal rotunda.png 		J34
Pentagonal orthobirotunda.png
Rhombicosidodecahedron
J5
Pentagonal cupola.png 		J72
Gyrate rhombicosidodecahedron.png 		J73
Parabigyrate rhombicosidodecahedron.png 		J74
Metabigyrate rhombicosidodecahedron.png 		J75
Trigyrate rhombicosidodecahedron.png 		J76
Diminished rhombicosidodecahedron.png 		J77
Paragyrate diminished rhombicosidodecahedron.png
J78
Metagyrate diminished rhombicosidodecahedron.png 		J79
Bigyrate diminished rhombicosidodecahedron.png 		J80
Parabidiminished rhombicosidodecahedron.png 		J81
Metabidiminished rhombicosidodecahedron.png 		J82
Gyrate bidiminished rhombicosidodecahedron.png 		J83
Tridiminished rhombicosidodecahedron.png

Se även

  •    Johnson, Norman W. (1966). "Konvexa fasta ämnen med regelbundna ytor" . Canadian Journal of Mathematics . 18 : 169–200. doi : 10.4153/cjm-1966-021-8 . ISSN 0008-414X . Zbl 0132.14603 . Innehåller den ursprungliga uppräkningen av de 92 fasta ämnena och gissningen att det inte finns några andra.
  •    Zalgaller, Victor A. (1967). "Konvex polyeder med regelbundna ansikten". Zap. Nauchn. Semin. Leningr. Otd. Matta. Inst. Steklova (på ryska). 2 : 1-221. ISSN 0373-2703 . Zbl 0165.56302 . Det första beviset på att det bara finns 92 Johnson-fastämnen. Engelsk översättning:    Zalgaller, Victor A. (1969). "Konvex polyeder med regelbundna ansikten". Seminarier i matematik, VA Steklov Math. Inst., Leningrad . Konsultbyrån. 2 . ISSN 0080-8873 . Zbl 0177.24802 .
  •   Anthony Pugh (1976). Polyhedra: Ett visuellt tillvägagångssätt . Kalifornien: University of California Press Berkeley. ISBN 0-520-03056-7 . Kapitel 3 Ytterligare konvexa polyedrar
  • Timofeenko, AV (2009). "Den icke-platoniska och icke-arkimediska icke-sammansatta polyedrarna". J. Math. Sci. 162 . 162 : 710-729. [1]

olyhedra." J. Math. Sci. 162, 710-729, 2009.

externa länkar

Hämtad från " https://en.wikipedia.org/w/index.php?title=Johnson_solid&oldid=1136197889 "