Pentagonal icositetrahedron

Pentagonal icositetrahedron
(Klicka ccw* eller cw för roterande modeller.)*
Typ	katalanska
Conway notation	gC
Coxeter diagram
Ansiktspolygon	oregelbunden femhörning
Ansikten	24
Kanter	60
Vertices	38 = 6 + 8 + 24
Ansiktskonfiguration	V3.3.3.3.4
Dihedral vinkel	136° 18' 33'
Symmetrigrupp	O , ½BC ₃ , [4,3] ⁺ , 432
Dubbel polyeder	snubb kub
Egenskaper	konvex , ansiktstransitiv , kiral
Netto

En geometrisk konstruktion av Tribonacci-konstanten (AC), med kompass och markerad linjal, enligt den metod som beskrivs av Xerardo Neira.

3D-modell av en femkantig icositetrahedron

Inom geometrin är en femkantig icositetrahedron eller pentagonal icosikaitetrahedron ett katalanskt fast ämne som är dual av snubkuben . Inom kristallografi kallas det också en gyroid .

Den har två distinkta former, som är spegelbilder (eller " enantiomorfer ") av varandra.

Konstruktion

Den femkantiga icositetrahedronen kan konstrueras av en snubkub utan att ta den dubbla. Fyrkantiga pyramider läggs till de sex fyrkantiga ytorna på snubbningskuben, och triangulära pyramider läggs till de åtta triangulära ytorna som inte delar en kant med en kvadrat. Pyramidens höjder är justerade för att göra dem i samma plan som de andra 24 triangulära ytorna på snubbningskuben. Resultatet är den femkantiga icositetrahedronen.

kartesiska koordinater

Beteckna tribonacci-konstanten med $t\approx 1.839\,286\,755\,21$ . (Se snub kub för en geometrisk förklaring av tribonacci-konstanten.) Sedan är kartesiska koordinater för de 38 hörnen av en femkantig icositetrahedron centrerad vid origo, följande:

de 12 jämna permutationerna av (±1, ±(2t+1), ±t ² ) med ett jämnt antal minustecken
de 12 udda permutationerna av (±1, ±(2t+1), ±t ² ) med ett udda antal minustecken
de 6 punkterna (±t ³ , 0, 0), (0, ±t ³ , 0) och (0, 0, ±t ³ )
de 8 punkterna (±t ² , ±t ² , ±t ² )

De konvexa skroven för dessa hörn skalade med $t^{-3}$ resulterar i en enhet circumradius oktaeder centrerad vid origo, en enhetskub centrerad vid origo skalad till $R\approx 0,9416969935$ och en oregelbunden kiral snubbkub skalad till $R$ , som visualiseras i figuren nedan:

Geometri

De femkantiga ytorna har fyra vinklar med $\arccos((1-t)/2)\approx 114.812,\4,074,\074,\ ^{\circ }$ och en vinkel av $\arccos(2-t)\approx 80.751\,702\,088\,39}^{\circ$ . Pentagonen har tre korta kanter av enhetslängd vardera och två långa kanter av längd $(t+1)/2\approx 1.419\,643\,377\ ,607\,08$ . Den spetsiga vinkeln är mellan de två långa kanterna. Den dihedriska vinkeln är lika med $\arccos(-1/(t^{2}-2))\approx 136.329,\,\ 892\,32^{\cirkel }$ .

Om dess dubbla snubkub har enhetskantlängd, är dess yta och volym:

{\displaystyle\begin{aligned}sq&rt \frac {22(5t-1)}{4t-3}}}&&\approx 19.299\,94\\V&={\sqrt {\frac {11(t-4)}{2(20t-37)} }}&&\approx 7.4474\end{aligned}}}

Ortogonala projektioner

Den femkantiga icositetraedern har tre symmetripositioner, två centrerade på hörn och en på mittkanten.

Ortogonala projektioner
Projektiv symmetri	[3]	[4] ⁺	[2]
Bild
Dubbel bild

Variationer

Isoedriska variationer med samma kirala oktaedriska symmetri kan konstrueras med femkantiga ytor med 3 kantlängder.

Denna variant som visas kan konstrueras genom att lägga till pyramider till 6 fyrkantiga ytor och 8 triangulära ytor av en snubbig kub så att de nya triangulära ytorna med 3 koplanära trianglar smälter samman till identiska femkantsytor.

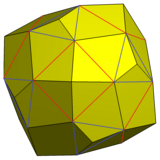Snub kub med utökade pyramider och sammanslagna ansikten	Pentagonal icositetrahedron	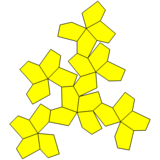Netto

Relaterade polyedrar och plattsättningar

Sfärisk femkantig icositetrahedron

Denna polyeder är topologiskt relaterad som en del av sekvensen av polyedrar och beläggningar av femhörningar med ansiktskonfigurationer (V3.3.3.3. n ). (Sekvensen fortskrider till att tillägga det hyperboliska planet till vilket n som helst .) Dessa ansiktstransitiva figurer har (n32) rotationssymmetri .

n 32 symmetrimutationer av snubbade plattsättningar: 3.3.3.3.n
Symmetri n 32	Sfärisk				euklidisk	Kompakt hyperbolisk		Paracomp.
Symmetri n 32	232	332	432	532	632	732	832	∞32
Snubbade figurer
Konfig.	3.3.3.3.2	3.3.3.3.3	3.3.3.3.4	3.3.3.3.5	3.3.3.3.6	3.3.3.3.7	3.3.3.3.8	3.3.3.3.∞
Gyrofigurer _
Konfig.	V3.3.3.3.2	V3.3.3.3.3	V3.3.3.3.4	V3.3.3.3.5	V3.3.3.3.6	V3.3.3.3.7	V3.3.3.3.8	V3.3.3.3.∞

Den femkantiga icositetrahedronen är tvåa i en serie av dubbla snubbade polyedrar och plattsättningar med ansiktskonfiguration V3.3.4.3. n .

4 n 2 symmetrimutationer av snubbade plattsättningar: 3.3.4.3.n
Symmetri 4 n 2	Sfärisk		euklidisk	Kompakt hyperbolisk				Paracomp.
Symmetri 4 n 2	242	342	442	542	642	742	842	∞42
Snubbiga figurer
Konfig.	3.3.4.3.2	3.3.4.3.3	3.3.4.3.4	3.3.4.3.5	3.3.4.3.6	3.3.4.3.7	3.3.4.3.8	3.3.4.3.∞
Gyrofigurer _
Konfig.	V3.3.4.3.2	V3.3.4.3.3	V3.3.4.3.4	V3.3.4.3.5	V3.3.4.3.6	V3.3.4.3.7	V3.3.4.3.8	V3.3.4.3.∞

Den femkantiga icositetraedern är en av en familj av dualer till de enhetliga polyedrarna relaterade till kuben och den vanliga oktaedern.

Uniforma oktaedriska polyedrar
Symmetri : [4,3], (*432)							[4,3] ⁺ (432)	[1 ⁺ ,4,3] = [3,3] (*332)		[3 ⁺ ,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{3 ^1,1 }	t{3,4} t{3 ^1,1 }	{3,4} {3 ^1,1 }	rr{4,3} s ₂ {3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h ₂ {4,3} t{3,3}	s{3,4} s{3 ^1,1 }

		=	=	=				= eller	= eller	=

Dual till enhetliga polyedrar
V4 ³	V3.8 ²	V(3.4) ²	V4.6 ²	V3 ⁴	V3.4 ³	V4.6.8	V3 ⁴ .4	V3 ³	V3.6 ²	V3 ⁵

Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design . Dover Publications, Inc. ISBN 0-486-23729-X . (Avsnitt 3-9)
Wenninger, Magnus (1983), Dual Models , Cambridge University Press , doi : 10.1017/CBO9780511569371 , ISBN 978-0-521-54325-5 , MR 0730208 (The thirteen semihedracular, Pentagraregular och 2 dux dux)
The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss , ISBN 978-1-56881-220-5 [1] (Kapitel 21, Naming the Archimedean and Catalan polyhedra and tilings, sida 287, pentagonal sektion )

externa länkar

Pentagonal Icositetrahedron – Interactive Polyhedron Model