Generaliserad logistisk distribution

Termen generaliserad logistisk fördelning används som namn på flera olika familjer av sannolikhetsfördelningar . Till exempel, Johnson et al. lista fyra former, som listas nedan.

Typ I har också kallats skew-logistic distribution . Typ IV subsumerar de andra typerna och erhålls när logittransformen tillämpas på beta - slumpvarianter. Enligt samma konvention som för log-normalfördelningen kan typ IV hänvisas till som sigmoid-beta-fördelningen , med hänvisning till den logistiska sigmoiden , som är inversen av logittransformen.

För andra familjer av distributioner som också har kallats generaliserade logistiska distributioner, se den förskjutna logistiska distributionen, som är en generalisering av den logistiska distributionen ; och metalog ("meta-logistic") distribution , som är mycket flexibel i form och gränser och kan anpassas till data med linjära minsta kvadrater.

Definitioner

Följande definitioner är för standardiserade versioner av familjerna, som kan utökas till den fullständiga formen som en platsskalig familj . Var och en definieras med antingen den kumulativa fördelningsfunktionen ( F ) eller sannolikhetstäthetsfunktionen ( ƒ ), och definieras på (-∞,∞).

Typ I

F(x;\alpha )={\frac {1}{( 1+e^{-x})^{\alpha }}}\equiv (1+e^{-x})^{-\alpha },\quad \alpha >0.

Motsvarande sannolikhetstäthetsfunktion är:

f(x;\alpha )={\frac {\alpha e^{-x}} {\left(1+e^{-x}\right)^{\alpha +1}}},\quad \alpha >0.

Denna typ har också kallats "skew-logistic" distribution.

Typ II

F(x;\alpha )=1-{\frac {e^{-\alpha x }}{(1+e^{-x})^{\alpha }}},\quad \alpha >0.

Motsvarande sannolikhetstäthetsfunktion är:

f(x;\alpha )={\frac {\alpha e^{-\alpha x}}{(1+e^{-x})^{\alpha +1}}},\quad \alpha >0.

Typ III

f(x;\alpha )={\frac {1}{ B(\alpha ,\alpha )}}{\frac {e^{-\alpha x}}{(1+e^{-x})^{2\alpha }}},\quad \alpha >0.

Här är B betafunktionen . Den momentgenererande funktionen för denna typ är

M(t)={\frac {\Gamma (\alpha -t)\Gamma (\alpha +t)}{(\Gamma (\alpha ))^{2}}},\quad -\alpha <t<\alpha .

Den motsvarande kumulativa fördelningsfunktionen är:

F(x;\alpha )={\frac {\left(e^{x}+1\right)\Gamma (\alpha )e^{ \alpha (-x)}\left(e^{-x}+1\right)^{-2\alpha }\,_{2}{\tilde {F}}_{1}\left(1, 1-\alpha ;\alpha +1;-e^{x}\right)}{B(\alpha ,\alpha )}},\quad \alpha >0.

Typ IV

{\begin{aligned}f(x;\alpha ,\beta )&={\frac {1}{B(\alpha ,\beta )}}{\frac {e^{-\beta x} }{(1+e^{-x})^{\alpha +\beta }}},\quad \alpha ,\beta >0\\[4pt]&={\frac {\sigma (x)^{ \alpha }\sigma (-x)^{\beta }}{B(\alpha ,\beta )}}.\end{aligned}}

Där B är betafunktionen och $\sigma$ är den logistiska sigmoiden . Den momentgenererande funktionen för denna typ är

M(t)={\frac {\Gamma (\beta -t)\Gamma (\alpha +t)}{\Gamma (\alpha )\Gamma (\beta)}},\quad -\alpha <t<\beta .

Denna typ kallas också för "exponentiell generaliserad beta av den andra typen".

Den motsvarande kumulativa fördelningsfunktionen är:

F(x;\alpha ,\beta )={\frac {\left(e^{x}+1\right)\ Gamma (\alpha )e^{\beta (-x)}\left(e^{-x}+1\right)^{-\alpha -\beta }\,_{2}{\tilde {F} }_{1}\left(1,1-\beta ;\alpha +1;-e^{x}\right)}{B(\alpha ,\beta )}},\quad \alpha ,\beta > 0.

Förhållande mellan typer

Typ IV är den mest allmänna formen av distributionen. Typ III-fördelningen kan erhållas från typ IV genom att fixera $\beta =\alpha$ . Typ II-fördelningen kan erhållas från typ IV genom att fixera $\alpha =1$ (och byta namn på $\beta$ till $\alpha$ ). Typ I-fördelningen kan erhållas från typ IV genom att fixera $\beta =1$ . Att fixera $\alpha =\beta =1$ ger standardlogistikfördelningen .

Typ IV (sigmoid-beta) egenskaper

Typ IV sannolikhetstäthetsfunktioner (medelvärde=0, varianser=1)

Typ IV generaliserade logistiska $\alpha ,\beta >0$ eller sigmoid-beta- distribution, med stöd för $x\in \mathbb {R}$ och formparametrarna , har ( som visas ovan ) sannolikhetstäthetsfunktionen (pdf):

f(x;\alpha ,\beta )={\frac {\sigma (x)^{\alpha }\sigma (-x)^{\beta }}{B(\alpha ,\beta )} }.

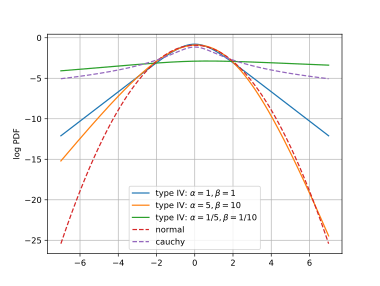
Pdf:erna för tre olika uppsättningar av formparametrar visas i diagrammet, där fördelningarna har skalats och skiftats för att ge noll medelvärden och enhetsvarianser, för att underlätta jämförelse av formerna.

Relation med Gamma Distribution

Denna fördelning kan erhållas i termer av gammafördelningen enligt följande. Låt $y\sim {\text{Gamma}}(\alpha ,1)$ och oberoende , $z\sim {\text{ Gamma}}(\beta ,1)$ och låt $x=\ln y-\ln z$ . Då har $x$ typ IV- fördelningen, med parametrarna $\alpha ,\beta$ .

Medelvärde, varians och skevhet

Genom att använda de logaritmiska förväntningarna på gammafördelningen kan medelvärdet och variansen härledas som:

{\begin{aligned}{\text{E}}[x]& =\psi (\alpha )-\psi (\beta )\\{\text{var}}[x]&=\psi '(\alpha )+\psi '(\beta )\\\end{aligned} }

där $\psi$ är digammafunktionen , medan $\psi '$ är dess första derivata, även känd som trigammafunktionen . På liknande sätt skevheten uttryckas i termer av tetragammafunktionen :

{\text{skew}}[x]=\psi ''(\alpha )-\psi ''(\beta )

tecken (och därmed handedness ) är detsamma som tecknet för $\alpha -\beta$ .

Läge

Läget (pdf maximum) kan härledas genom att hitta $x$ där log pdf-derivatan är noll:

{\frac {d}{dx}}\ln f(x;\alpha ,\ beta )=\alpha \sigma (-x)-\beta \sigma (x)=0

Detta förenklar till ${\displaystyle \alpha /\beta =e^{x}} ,$ så att:

{\text{läge}}[x]=\ln {\frac {\alpha }{\beta }}

Svansbeteende

Svansjämförelse: Typ IV (medel=0, varianser=1) vs standard normal , vs standard Cauchy

I var och en av vänster och höger svans mättas en av sigmoiderna i pdf:en till en, så att svansen bildas av den andra sigmoiden. För stora negativa $x$ är den vänstra svansen av pdf:en proportionell mot $\sigma (x)^{\alpha }\approx e^{\alpha x}$ , medan den högra svansen (stor positiv $x$ ) är proportionell mot $\sigma (-x)^{\beta }\approx e^{- \beta x}$ . Detta betyder att svansarna styrs oberoende av $\alpha$ och $\beta$ . Även om svansar av typ IV är tyngre än normalfördelningen ( e $\displaystyle e^{-{\frac {x^{2}}{2v}}}},$ för varians $v$ ), förblir typ IV medelvärden och varianser ändliga för alla $\alpha ,\beta >0$ . Detta står i kontrast till Cauchy-fördelningen för vilken medelvärdet och variansen inte existerar. I log pdf-plotterna som visas här är svansarna av typ IV linjära, normalfördelningssvansarna är kvadratiska och Cauchy-svansarna är logaritmiska.

Relationer med andra distributioner

Relationer med andra distributioner inkluderar:

Om $y\sim {\text{BetaPrime}}(\alpha ,\beta )$ , så har ${\displaystyle x=\ln y} en$ typ IV distribution, med parametrarna $\alpha$ och $\beta$ . Se betaprimefördelning .
Om $z\sim {\text{Gamma}}(\beta ,1)$ och $y\sim {\text{Gamma} }(\alpha ,z)$ , där $z$ används som hastighetsparameter för den andra gammafördelningen, då har $y$ en sammansatt gammafördelning , som är samma som ${\text{BetaPrime}}(\alpha ,\beta )$ , så att $x=\ln y$ har en typ IV- fördelning.
Om $p\sim {\text{Beta}}(\alpha ,\beta )$ , då $x={\text{logit}}\, p$ har en typ IV- fördelning, med parametrarna $\alpha$ och $\beta$ . Se betadistribution . Logitfunktionen , $\log {\frac {p}{1-p}}$ är inversen av den logistiska sigmoiden. Detta förhållande förklarar namnet sigmoid-beta för denna distribution: om sigmoid appliceras på sigmoid-beta-variationer är den transformerade fördelningen beta.

Stora formparametrar

Typ IV vs normalfördelning (medelvärde=0, varianser = 1). För stora värden på

\alpha ,\beta

, är pdf-filerna väldigt lika, förutom mycket sällsynta värden på

x

.

För stora värden på formparametrarna, ${\displaystyle \alpha ,\beta \gg 1} ,$ blir fördelningen mer gaussisk . Detta visas i pdf- och log-pdf-plotterna här.

Slumpmässig variationsgenerering

Eftersom slumpmässigt urval från gamma- och betadistributionerna är lättillgängliga på många programvaruplattformar, kan ovanstående relationer med dessa distributioner användas för att generera variationer från typ IV-distributionen.

Generalisering med plats- och skalparametrar

En flexibel familj med fyra parametrar kan erhållas genom att lägga till plats- och skalparametrar . Återigen, låt $y\sim {\text{Gamma}}(\alpha ,1)$ och $z\sim {\text{ Gamma}}(\beta ,1)$ och nu mer allmänt låt

x=\mu +s(\ln y-\ln z)

.

där $\mu \in \mathbb {R}$ och $s>0$ , då är den resulterande pdf:en:

f(x;\alpha ,\beta , \mu ,s)={\frac {\sigma ({\frac {x-\mu }{s}})^{\alpha }\sigma (-{\frac {x-\mu }{s}}) ^{\beta }}{sB(\alpha ,\beta )}}

Medelvärdet och variansen är nu:

{\begin{ aligned}{\text{E}}[x]&=\mu +s(\psi (\alpha )-\psi (\beta ))\\{\text{var}}[x]&=s^{ 2}(\psi ^{(1)}(\alpha )+\psi ^{(1)}(\beta ))\\\end{aligned}}

Maximal likelihood-parameteruppskattning

Eftersom (logaritmerna för) sigmoid- och betafunktionerna är lätt tillgängliga i mjukvarupaket med automatisk differentiering , kan gradienter av log-pdf med avseende på parametrarna lätt erhållas, så att gradientbaserad numerisk optimering kan användas för att göra maximal sannolikhetsuppskattningar av parametrarna för denna fördelning.

Se även

Champernowne distribution , en annan generalisering av den logistiska distributionen.

^ ^a ^b Johnson, NL, Kotz, S., Balakrishnan, N. (1995) Continuous Univariate Distributions, Volym 2 , Wiley. ISBN 0-471-58494-0 (sidorna 140–142)
^ ^a ^b ^c Leigh J. Halliwell (2018). "Log-gamma-distributionen och icke-normalt fel" . Hämtad 22 februari 2023 . {{ citera journal }} : Citera journal kräver |journal= ( hjälp )

[J1-1] Johnson, NL, Kotz, S., Balakrishnan, N. (1995) Continuous Univariate Distributions, Volym 2 , Wiley. ISBN 0-471-58494-0 (sidorna 140–142)

[Haliwell-2] Leigh J. Halliwell (2018). "Log-gamma-distributionen och icke-normalt fel" . Hämtad 22 februari 2023 . {{ citera journal }} : Citera journal kräver |journal= ( hjälp )