Metalog distribution

Tre-term metalog distributioner

Fyrterms metalogfördelning när $a_{3}=0$

Metalogfördelningen är en flexibel kontinuerlig sannolikhetsfördelning utformad för enkel användning i praktiken . Tillsammans med sina transformationer är metalogfamiljen av kontinuerliga distributioner unik eftersom den förkroppsligar alla följande egenskaper: praktiskt taget obegränsad formflexibilitet; ett val mellan obundna, semi-bounded och bounded distributioner; enkel anpassning till data med linjära minsta kvadrater; kvantilfunktionsekvationer i sluten form (invers CDF ) som underlättar simulering ; en enkel, sluten PDF ; och Bayesiansk uppdatering i sluten form i ljuset av nya data. Dessutom, precis som en Taylor-serie , kan metalogdistributioner ha valfritt antal termer, beroende på graden av önskad formflexibilitet och andra applikationsbehov.

Tillämpningar där metalogfördelningar kan vara användbara involverar typiskt anpassning av empiriska data, simulerade data eller expertframkallade kvantiler för att jämna, kontinuerliga sannolikhetsfördelningar. Användningsområdena är omfattande och inkluderar ekonomi, vetenskap, teknik och många andra områden. Metalog-distributionerna, även kända som Keelin-distributionerna, publicerades först 2016 av Tom Keelin.

Historia

Sannolikhetsfördelningarnas historia kan delvis ses som en utveckling av utvecklingen mot större flexibilitet i form och gränser vid anpassning till data . Normalfördelningen publicerades första gången 1756, och Bayes sats 1763. Normalfördelningen lade grunden för mycket av den klassiska statistikens utveckling . Däremot lade Bayes teorem grunden för informationstillståndet, trosbaserade sannolikhetsrepresentationer. Eftersom trosbaserade sannolikheter kan anta vilken form som helst och kan ha naturliga gränser, behövdes sannolikhetsfördelningar som var tillräckligt flexibla för att rymma båda. Dessutom uppvisade många empiriska och experimentella datamängder former som inte kunde matchas väl av normala eller andra kontinuerliga distributioner . Så började sökandet efter kontinuerliga sannolikhetsfördelningar med flexibla former och gränser.

Tidigt på 1900-talet uppstod Pearson- familjen av distributioner, som inkluderar normal , beta , uniform , gamma , student-t , chi-square , F och fem andra, som ett stort framsteg i formflexibilitet. Dessa följdes av Johnson- utdelningarna. Båda familjerna kan representera de första fyra momenten av data ( medelvärde , varians , skevhet och kurtos ) med jämna kontinuerliga kurvor. Däremot har de ingen förmåga att matcha ögonblick av femte eller högre ordningen. Dessutom, för en given skevhet och kurtosis finns det inget val av gränser. Till exempel kan matchning av de första fyra momenten i en datamängd ge en fördelning med en negativ nedre gräns, även om det kan vara känt att kvantiteten i fråga inte kan vara negativ. Slutligen inkluderar deras ekvationer svårlösta integraler och komplexa statistiska funktioner, så att anpassning till data vanligtvis kräver iterativa metoder.

Tidigt på 2000-talet började beslutsanalytiker arbeta med att utveckla kontinuerliga sannolikhetsfördelningar som exakt skulle passa alla specificerade tre punkter på den kumulativa fördelningsfunktionen för en osäker kvantitet (t.ex. expertutlöst $0.10,0.50$ och $0,90$ kvantiler). Pearson- och Johnson-familjens distributioner var i allmänhet otillräckliga för detta ändamål. Dessutom sökte beslutsanalytiker också sannolikhetsfördelningar som skulle vara lätta att parametrisera med data (t.ex. genom att använda linjära minsta kvadrater eller motsvarande multipel linjär regression ). Introducerad 2011, uppnådde klassen av kvantilparameteriserade distributioner (QPD) båda målen. Även om det var ett betydande framsteg av denna anledning, användes QPD ursprungligen för att illustrera denna klass av distributioner, Simple Q-Normal-fördelningen, hade mindre formflexibilitet än Pearson- och Johnson-familjerna och saknade förmågan att representera semi-bounded och bounded distributions . Kort därefter utvecklade Keelin familjen av metalogdistributioner, en annan instans av QPD-klassen, som är mer formflexibel än Pearson- och Johnson-familjerna, erbjuder ett val av begränsning, har sluten formekvationer som kan anpassas till data med linjär kvantilfunktioner i sluten form, vilket underlättar Monte Carlo-simulering .

Definition och kvantilfunktion

Metalogdistributionen är en generalisering av den logistiska distributionen , där termen "metalog" är en förkortning för "metalogistisk". Börjar med den logistiska kvantilfunktionen , $x=Q(y)=\mu +s{\mbox{ }}\ln {\Bigl (}{y \över {1-y}}{\Bigr )}$ , Keelin ersatte potensserieexpansionerna i kumulativ sannolikhet $y=F(x)$ för $\ mu$ och parametrarna $s$ , som styr plats respektive skala.

$\mu =a_{1 }+a_{4}(y-0.5)+a_{5}(y-0.5)^{2}+a_{7}(y-0.5)^{3}+a_{9}(y-0.5)^ {4}+\dots$

${\ displaystyle s=a_{2}+a_{3}(y-0.5)+a_{6}(y-0.5)^{2}+a_{8}(y-0.5)^{3}+a_{10} (y-0,5)^{4}+\dots }$

Keelins motivering för detta utbyte var femfaldigt. För det första skulle den resulterande kvantilfunktionen ha betydande formflexibilitet, styrd av koefficienterna $a_{i}$ . För det andra skulle det ha en enkel sluten form som är linjär i dessa koefficienter, vilket antyder att de lätt kan bestämmas från CDF- data genom linjära minsta kvadrater . För det tredje skulle den resulterande kvantilfunktionen vara jämn, differentierbar och analytisk , vilket säkerställer att en jämn, sluten PDF -fil är tillgänglig. För det fjärde simulering underlättas av den resulterande inversa CDF i sluten form . För det femte, som en Taylor-serie , kan valfritt antal termer $k$ användas, beroende på graden av önskad formflexibilitet och andra applikationsbehov.

Observera att sänkningarna av $a$ -koefficienterna är sådana att $a_{1}$ och $a_{4}$ är i expansionen ${\displaystyle \mu } ,$$a_{2}$ och $a_{3}$ finns i $s$ -expansionen, och abonnemang växlar därefter. Denna ordning valdes så att de två första termerna i den resulterande metalogkvantilfunktionen exakt motsvarar den logistiska fördelningen; $a_{3}\neq 0$ tredje term med justerar skevhet; lägga till $a_{4}\neq 0$ fjärde term med justerar kurtos primärt; och att lägga till efterföljande termer som inte är noll ger mer nyanserade formförfinningar.

Att skriva om den logistiska kvantilfunktionen för att införliva ovanstående ersättningar för $\mu$ och $s$ ger metalog- kvantilfunktionen , för kumulativ sannolikhet $0<y<1$ .

$M_{k}(y)=\left\{{\begin{array}{ll}a_{1}+a_{2}\ln {\Bigl (}{y \over {1 -y}}{\Bigr )}&{\mbox{för }}k=2\\a_{1}+a_{2}\ln {\Bigl (}{y \över {1-y}}{\ Bigr )}+a_{3}(y-0.5)\ln {\Bigl (}{y \over {1-y}}{\Bigr )}&{\mbox{för }}k=3\\a_{ 1}+a_{2}\ln {\Bigl (}{y \over {1-y}}{\Bigr )}+a_{3}(y-0.5)\ln {\Bigl (}{y \over {1-y}}{\Bigr )}+a_{4}(y-0.5)&{\mbox{för }}k=4\\M_{k-1}(y)+a_{k}(y -0.5)^{k-1 \över 2}&{\mbox{för udda }}k\geq 5\\M_{k-1}(y)+a_{k}(y-0.5)^{{k \over 2}-1}\ln {\Bigl (}{y \over {1-y}}{\Bigr )}&{\mbox{för även }}k\geq 6\\\end{array}} \höger.$

På motsvarande sätt kan metalog-kvantilfunktionen uttryckas i termer av basfunktioner: $M_{k}(y)=\summa _{i= 1}^{k}a_{i}g_{i}(y)$ , där metalogbasfunktionerna är ${\ displaystyle g_{1}(y)=1,{\mbox{ }}g_{2}(y)=\ln {\Bigl (}{y \over {1-y}}{\Bigr )},}$ och varje efterföljande $g_{i}(y)$ definieras som uttrycket som multipliceras med $a_{i}$ i ekvationen för $M_ {k}(y)$ ovan. Observera att koefficienten $a_{1}$ är medianen eftersom alla andra termer är lika med noll när $y=0,5$ . Specialfall av metalog-kvantilfunktionen är den logistiska fördelningen ( $k=2$ ) och den enhetliga fördelningen ( $k\ geq 4,a_{1}=0.5,a_{4}=1,a_{i}=0$ annars).

Sannolikhetstäthetsfunktion

Att differentiera $x=M_{k}(y)$ med avseende på $y$ ger kvantildensitetsfunktionen $q( y)=dx/dy$ . Det ömsesidiga av denna kvantitet, $(q(y))^{-1}=dy/dx=f(Q (y))$ , är sannolikhetstäthetsfunktionen uttryckt som en p-PDF,

$m_ {k}(y)=\left\{{\begin{array}{ll}{y(1-y) \over {a_{2}}}&{\mbox{för }}k=2\\{ \Bigl (}{a_{2} \över {y(1-y)}}+a_{3}{\Bigl (}{y-0.5 \over {y(1-y)}}+\ln {y \över {1-y}}{\Bigr )}{\Bigr )}^{-1}&{\mbox{för }}k=3\\{\Bigl (}{a_{2} \över {y (1-y)}}+a_{3}{\Bigl (}{y-0.5 \over {y(1-y)}}+\ln {y \over {1-y}}{\Bigr )} +a_{4}{\Bigr )}^{-1}&{\mbox{för }}k=4\\{\Bigl (}{1 \över {m_{k-1}(y)}}+ a_{k}{k-1 \över 2}(y-0.5)^{(k-3)/2}{\Bigr )}^{-1}&{\mbox{för udda }}k\geq 5 \\{\Bigl (}{1 \över {m_{k-1}(y)}}+a_{k}{\Bigl (}{(y-0.5)^{k/2-1} \över { y(1-y)}}+({k \over 2}-1)(y-0.5)^{(k/2-2)}\ln {y \over {1-y}}{\Bigr ) }{\Bigr )}^{-1}&{\mbox{för jämn }}k\geq 6,\\\end{array}}\right.}$

som kan uttryckas likvärdigt i termer av basfunktioner som

${\displaystyle m_{k}(y)=\left(\summa _{i=1}^{k }a_{i}{{dg_{i}(y)} \över {dy}}\right)^{-1}} där < y < 1 {\displaystyle$ where $0<y<1$.

Observera att denna PDF uttrycks som en funktion av kumulativ sannolikhet, $y$ , snarare än variabel av intresse, $x$ . För att plotta PDF-filen (t.ex. som visas i figurerna på denna sida), kan man variera $y\in (0,1)$ parametriskt, och sedan plotta $x=M_{k}(y)$ på den horisontella axeln och $m_{k}(y)$ på den vertikala axeln.

Baserat på ovanstående ekvationer och följande transformationer som möjliggör val av gränser, består familjen av metalogfördelningar av obundna, semibounded och bounded metalogs, tillsammans med deras symmetrisk-percentile triplett (SPT) specialfall.

Ogränsade, semi-bounded och bounded metalogdistributioner

Som definierats ovan är metalogfördelningen obegränsad, förutom i det ovanliga specialfallet där $a_{i}=0$ för alla termer som innehåller $\ln {\ Bigl (}{y \over {1-y}}{\Bigr )}$ . Men många applikationer kräver flexibla sannolikhetsfördelningar som har en nedre gräns $b_{l}$ , en övre gräns $b_{u}$ , eller båda. För att möta detta behov använde Keelin transformationer för att härleda semi-bounded och bounded metalog distributioner. Sådana transformationer styrs av en allmän egenskap hos kvantilfunktioner: för valfri kvantilfunktion $x=Q(y)$ och ökande funktion $z(x),x=z^{-1}(Q(y))$ är också en kvantilfunktion . Till exempel är kvantilfunktionen för normalfördelningen $x=\mu +\sigma \Phi ^{-1}(y)$ ; eftersom den naturliga logaritmen, $z(x)=\ln(x-b_{l})$ , är en ökande funktion, $x=b_{l}+e^{\mu +\sigma \Phi ^{-1}(y)}$ är kvantilfunktionen för lognormalfördelningen . Analogt, applicering av denna egenskap på metalog-kvantilfunktionen $M_{k}(y)$ med hjälp av transformationerna nedan ger de semi-bounded och bounded medlemmarna av metalog-familjen Genom att betrakta $z(x)$ som metalogfördelad, uppfyller alla medlemmar av metalogfamiljen Keelin och Powleys definition av en kvantilparameteriserad fördelning och har därmed egenskaperna därav.

${\begin{array}{l|c|c|c|c|c}&&&&&{ \mbox{form}}\\&{\mbox{transformation}}&{\mbox{kvantilfunktion}}&{\mbox{PDF}}&{\mbox{där}}&{\mbox{parametrar}}\ \\hline {\mbox{Metalog (unbounded)}}&z(x)=x&M_{k}(y)&m_{k}(y)&0<y<1&k-2\\\hline {\mbox{Log metalog} }&z(x)=\ln(x-b_{l})&M_{k}^{\log(}y)=b_{l}+e^{M_{k}(y)}&m_{k}^ {\log(}y)=m_{k}(y)e^{-M_{k}(y)}&0<y<1&k-1\\{\mbox{(avgränsat nedan)}}&&=b_{ l}&=0&y=0\\\hline {\mbox{Negative-log metalog}}&z(x)=-\ln(b_{u}-x)&M_{k}^{\operatörsnamn {nlog} }( y)=b_{u}-e^{-M_{k}(y)}&m_{k}^{\operatörsnamn {nlog} }(y)=m_{k}(y)e^{M_{k} (y)}&0<y<1&k-1\\{\mbox{(avgränsat ovan)}}&&=b_{u}&=0&y=1\\\hline {\mbox{Logit metalog}}&z(x) =\ln {\Bigl (}{x-b_{l} \over {b_{u}-x}}{\Bigr )}&M_{k}^{\operatörsnamn {logit} }(y)={b_{ l}+b_{u}e^{M_{k}(y)} \över {1+e^{M_{k}(y)}}}&m_{k}^{\operatörsnamn {logit} }(y )=m_{k}(y){{\bigl (}1+e^{M_{k}(y)}{\bigr )}^{2} \över {(b_{u}-b_{l} )e^{M_{k}(y)}}}&0<y<1&k\\{\mbox{(bounded)}}&&=b_{l}&=0&y=0\\&&=b_{u}& =0&y=1\end{array}}$

Observera att antalet formparametrar i metalogfamiljen ökar linjärt med antalet termer $k$ . Därför kan vilken som helst av ovanstående metaloger ha vilket antal formparametrar som helst. Däremot är Pearson- och Johnson-familjerna av distributioner begränsade till två formparametrar.

SPT metalog distributioner

Begränsad SPT metalog parametriserad med CDF-data $(20,0.1),(30,0.5),$ och $(50,0.9)$ och med nedre och övre gränser $0$ respektive $100$ .

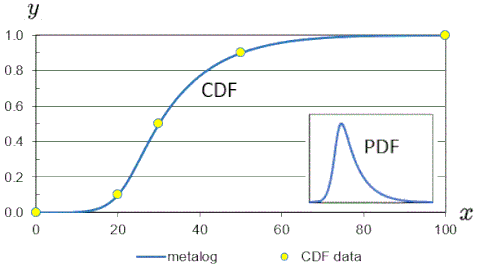
Metalogfördelningarna med symmetrisk-percentil-triplett (SPT) är en treterm $(k=3)$ specialfall av de obundna, semi-bounded och bounded metalog-fördelningarna. Dessa parametriseras av de tre $(x,y)$ punkterna utanför CDF-kurvan , av formen $(x_{1},\alpha )$ , $(x_{2},0.5)$ , och $(x_{3},1-\alpha )$ , där ${\ displaystil 0<\alpha <0.5}$ . SPT metalogs är användbara när, till exempel, kvantiler $(x_{1},x_{2},x_{3})$ som motsvarar CDF-sannolikheterna (t.ex. $0.1,0.5,0.9$ ) framkallas från en expert och används för att parametrisera de tre termiga metalogfördelningarna. Som noteras nedan förenklas vissa matematiska egenskaper genom SPT-parameterisering.

Egenskaper

Metalogfamiljen av sannolikhetsfördelningar har följande egenskaper.

Genomförbarhet

En funktion av formen av $M_{k}(y)$ eller någon av dess transformationer ovan är en möjlig sannolikhetsfördelning om och endast om dess PDF är större än noll för alla $y\in (0,1).$ Detta innebär en genomförbarhetsbegränsning på uppsättningen av koefficienter ${\boldsymbol {a}}= (a_{1},...,a_{k})\in \mathbb {R} ^{k}$ ,

$m_{k}(y)>0$ för alla $\displaystyle y\in (0,1)}$ .

I praktiska tillämpningar måste genomförbarheten generellt kontrolleras snarare än antas. För $k=2$ säkerställer $a_{2}>0} genomförbarhet.$ displaystyle För $k=3$ (inklusive SPT metalogs), är genomförbarhetsvillkoret $a_{2}>0$ och ${|a_{3}|/a_{2}}<1.66711$ . För $k=4$ har en liknande sluten form härletts. För $k\geq 5$ kontrolleras genomförbarheten vanligtvis grafiskt eller numeriskt.

Den obegränsade metalogen och dess transformationer ovan delar samma uppsättning möjliga koefficienter. Därför, för en given uppsättning koefficienter, bekräftar att $m_{k}(y)>0$ för alla ${\displaystyle y\in (0,1)$ räcker oavsett vilken transformation som används.

Konvexitet

Uppsättningen av möjliga metalogkoefficienter $S_{\boldsymbol {a}}=\{{\boldsymbol {a}}\in \mathbb {R} ^{k}|m_{k}(y)>0$ för all $y\in (0,1)\}$ är konvex . Eftersom konvexa optimeringsproblem kräver konvexa genomförbara uppsättningar, kan den här egenskapen förenkla optimeringsproblem som involverar metalogs. Dessutom garanterar den här egenskapen att varje konvex kombination av ${\displaystyle {\boldsymbol {a}}}-$ vektorerna för genomförbara metaloger är genomförbar, vilket är användbart till exempel när man kombinerar åsikter från flera experter eller interpolerar mellan genomförbara metaloger. Underförstått är varje probabilistisk blandning av metalogfördelningar i sig en metalog.

Anpassning till data

10-terms log metalog-fördelning över den maximala årliga flodmätarhöjden (ft) från 1920 till 2014 för Williamsonfloden nedanför Sprague River-sammanflödet, Chiloquin, Oregon. Datakälla: USGS .

Koefficienterna ${\boldsymbol {a}}$ kan bestämmas från data genom linjära minsta kvadrater . Givet $n$ datapunkter $(x_{i},y_{i})$ som är avsedda att karakterisera en metalog CDF, och en $n\ gånger k$ matris ${\boldsymbol {Y}}$ vars element består av basfunktionerna $g_{j}(y_{i})$ , sedan så länge som ${\boldsymbol {Y}}^{T}{\boldsymbol {Y}}$ är inverterbar, kolumnvektorn ${\boldsymbol {a}}$ av koefficienterna $a_ {i}$ ges av ${\boldsymbol {a}}=({\boldsymbol {Y}}^{T}{\boldsymbol {Y}}) ^{-1}{\boldsymbol {Y}}^{T}{\boldsymbol {z}}$ , där $n\geq k$ och kolumnvektor ${\boldsymbol {z}}=(z(x_{1}),\ldots ,z(x_{n}))$ . Om $n=k$ reduceras denna ekvation till ${\boldsymbol {a}}={\boldsymbol {Y}}^{-1}{\boldsymbol {z }}$ , där den resulterande metalogen CDF kör igenom alla datapunkter exakt. För SPT-metaloger reduceras det ytterligare till uttryck i termer av de tre $(x_{i},y_{i})$ punkterna direkt.

En alternativ anpassningsmetod, implementerad som ett linjärt program, bestämmer koefficienterna genom att minimera summan av absoluta avstånd mellan CDF och data, med förbehåll för genomförbarhetsbegränsningar.

Hur metaloger konvergerar till standardnormalfördelning när $k$ ökar från 2 till 10

Weibull-fördelningar (blå) nära approximerade av nio-terms semi-bounded metalog-fördelningar (streckade, gula)

Formflexibilitet

Enligt metalogens flexibilitetssats kan varje sannolikhetsfördelning med en kontinuerlig kvantilfunktion approximeras godtyckligt noggrant av en metalog. Dessutom visade Keelin i den ursprungliga artikeln att tiotermsmetalogfördelningar parametriserade med 105 CDF-poäng från 30 traditionella källfördelningar (inklusive normal-, student-t-, lognormal-, gamma-, beta- och extremvärdesfördelningar) approximerar varje sådan källa distribution inom ett KS- avstånd på 0,001 eller mindre. Sålunda är metalogformflexibiliteten praktiskt taget obegränsad.

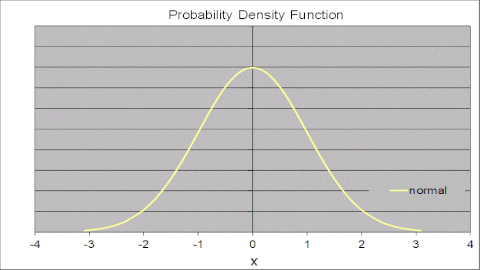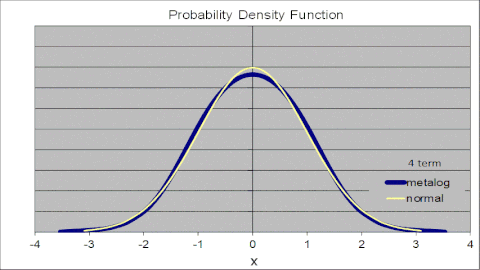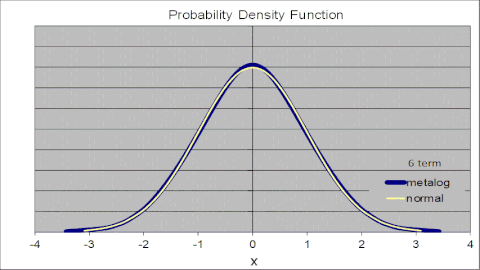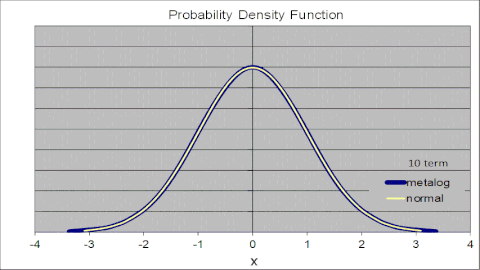
Den animerade figuren till höger illustrerar detta för standardnormalfördelningen, där metaloger med olika antal termer parametriseras av samma uppsättning av 105 punkter från standardnormal CDF. Metalog PDF konvergerar till den vanliga normala PDF-filen när antalet termer ökar. Med två termer approximerar metalogen normalen med en logistisk fördelning. Med varje ökning i antal termer kommer passformen närmare. Med 10 termer är metalog PDF och standard normal PDF visuellt omöjliga att skilja.

På liknande sätt är nio-terms semi-bounded metalog PDF-filer med $b_{l}=0$ visuellt omöjliga att skilja från en rad Weibull-distributioner . De sex fallen som visas till höger motsvarar Weibulls formparametrar 0.5, 0.8, 1.0, 1.5, 2 och 4. I varje fall parametriseras metalogen av de nio x {\displaystyle x} $från$ Weibull CDF som motsvarar de kumulativa sannolikheterna $y=(0,001,0,02,0,0,0,0,0,0,0,0,0,0,0,0,0,5,0,0,0,0,0,0,0,0,0,0,0,0,0,5 ,0,999)$ .

Sådan konvergens är inte unik för normal- och Weibull-fördelningarna. Keelin visade ursprungligen analoga resultat för ett brett utbud av distributioner och har sedan dess tillhandahållit ytterligare illustrationer.

Median

Medianen för varje distribution i metalogfamiljen har en enkel sluten form. Observera att $y=0.5$ definierar medianen, och $M_{k}(0.5)=a_{1}$ (eftersom alla efterföljande termer är noll för $y=0,5$ ). Det följer att medianerna för de obegränsade metalog-, log-metalog-, negativ-log metalog- och logit-metalog-fördelningarna är $a_{1}$ , $b_{l}+e^ {a_{1}}$ , $b_{u}-e^{-a_{1}}$ och ${\ displaystyle {b_{l}+b_{u}e^{a_{1}} \över {1+e^{a_{1}}}}} ,$ respektive.

Ögonblick

Momentet $m^{th}$ för den obundna metalogfördelningen, ${\displaystyle E[x^{m}]= \int _{y=0}^{1}{M_{k}(y)}^{m}\,dy} ,$ är ett specialfall av den mer allmänna formeln för QPD. För den obegränsade metalogen utvärderas sådana integraler till moment i sluten form som är $m^{th}$ ordningens polynom i koefficienterna $a_{i}$ . De fyra första centrala momenten i den fyra termiska ogränsade metalogen är:

${\begin{aligned}{\text{mean}}={}&a_{1}+{a_{3} \over 2}\\[6pt]{\text{ varians}}={}&\pi ^{2}{{a_{2}}^{2} \over 3}+{{a_{3}}^{2} \over {12}}+\pi ^ {2}{{a_{3}}^{2} \over {36}}+a_{2}a_{4}+{{a_{4}}^{2} \over {12}}\\[ 6pt]{\text{skewness}}={}&\pi ^{2}{a_{2}}^{2}{a_{3}}+\pi ^{2}{{a_{3}}^ {3} \over {24}}+{{{a_{2}}{a_{3}}{a_{4}}} \over {2}}+\pi ^{2}{{{a_{2 }}{a_{3}}{a_{4}}} \över {6}}+{{{a_{3}}{a_{4}}^{2}} \över {8}}\\[ 6pt]{\text{kurtosis}}={}&7\pi ^{4}{{a_{2}}^{4} \över {15}}+3\pi ^{2}{{{a_{2 }}^{2}{a_{3}}^{2}} \over {24}}+7\pi ^{4}{{{a_{2}}^{2}{a_{3}}^ {2}} \over {30}}+{{{a_{3}}^{4}} \over {80}}+\pi ^{2}{{a_{3}}^{4} \over {24}}+7\pi ^{4}{{a_{3}}^{4} \over {1200}}+2\pi ^{2}{a_{2}}^{3}{a_{ 4}}\\[6pt]&{}+{{{a_{2}}{a_{3}}^{2}{a_{4}}} \över {2}}+2\pi ^{2 {{{a_{2}}{a_{3}}^{2}{a_{4}}} \over {3}}+2{{a_{2}}^{2}{a_{4} }^{2}}+\pi ^{2}{{{a_{2}}^{2}{a_{4}}^{2}} \över {6}}+{{{a_{3} }^{2}{a_{4}}^{2}} \över {8}}+\pi ^{2}{{{a_{3}}^{2}{a_{4}}^{2 }} \over {40}}+{{{a_{2}}{a_{4}}^{3}} \over {3}}+{{a_{4}}^{4} \over {80 }}\end{aligned}}$

Moment för färre termer ingår i dessa ekvationer. Till exempel kan moment av tretermmetalogen erhållas genom att ställa in $a_{4}$ till noll. Moment för metalogs med fler termer och högre ordningens moment ( $m>4$ ), är också tillgängliga. Moment för semi-bounded och bounded metalogs är inte tillgängliga i sluten form.

Parametrering med moment

Tre-term unbounded metalogs kan parametriseras i sluten form med sina tre första centrala moment . Låt $m,v,$ och $s$ vara medelvärdet, variansen och skevheten, och låt $s_{s}$ vara den standardiserade skevheten, $s_{s}=s/v^{3/2}$ . Ekvivalenta uttryck för momenten i termer av koefficienter och koefficienter i termer av moment, är följande:

${\begin{array}{ll}m=a_{1}+{a_{3} \över 2}&&a_ {1}=m-{a_{3} \over 2}\\[6pt]v=\pi ^{2}{{a_{2}}^{2} \over 3}+{{a_{3} }^{2} \over {12}}+\pi ^{2}{{a_{3}}^{2} \over {36}}&&a_{2}={1 \over {\pi }}{ \Bigl [}3{\Bigl (}v-{\Bigl (}{1 \over {12}}+{{\pi }^{2} \over {36}}{\Bigr )}{a_{3 }}^{2}{\Bigr )}{\Bigr ]}^{1 \över {2}}\\[6pt]s=\pi ^{2}{a_{2}}^{2}{a_ {3}}+\pi ^{2}{{a_{3}}^{3} \over {24}}&&a_{3}=4{\Bigl (}{6v \over {6+\pi ^{ 2}}}{\Bigr )}^{1 \over {2}}\cos {\Bigl [}{1 \over {3}}{\Bigl (}\cos ^{-1}{\Bigl (} -{s_{s} \over {4}}{\Bigl (}1+{{\pi }^{2} \over {6}}{\Bigr )}^{1 \over {2}}{\ Bigr )}+4\pi {\Bigr )}{\Bigr ]}\\[6pt]\end{array}}$

Ekvivalensen för dessa två uppsättningar uttryck kan härledas genom att notera att momentekvationerna till vänster bestämmer ett kubiskt polynom i termer av koefficienterna $a_{1},a_{2},$ och $a_{3}$ , som kan lösas i sluten form som funktioner av $m,v,$ och $s$ . Dessutom är denna lösning unik. När det gäller moment är genomförbarhetsvillkoret ${\displaystyle |s_{s}|\leq 2.07093} ,$ vilket kan visas vara ekvivalent med följande genomförbarhetsvillkor vad gäller koefficienterna: $a_{2}>0$ ; och ${|a_{3}|/a_{2}}<1.66711$ .

Den här egenskapen kan till exempel användas för att representera summan av oberoende, icke-identiskt fördelade slumpvariabler . Baserat på kumulanter är det känt att för varje uppsättning oberoende slumpvariabler är medelvärdet, variansen och skevheten för summan summan av respektive medelvärde, varianser och skevheter. Parametrering av en tre-term metalog med dessa centrala moment ger en kontinuerlig fördelning som exakt bevarar dessa tre moment, och ger följaktligen en rimlig approximation till formen av fördelningen av summan av oberoende slumpvariabler.

Simulering

Eftersom deras kvantilfunktioner uttrycks i sluten form, underlättar metalogs Monte Carlo-simulering . Genom att ersätta enhetligt fördelade slumpmässiga sampel av $y$ i Metalog- kvantilfunktionen (invers CDF) produceras slumpmässiga sampel av $x$ i sluten form, vilket eliminerar behovet av att invertera en CDF. Se nedan för simuleringsapplikationer.

Framkalla och kombinera expertutlåtanden

På grund av sin formflexibilitet kan metalogdistributioner vara ett attraktivt val för att framkalla och representera expertutlåtanden. Dessutom, om åsikterna från flera experter uttrycks som $k$ -term metalogs, kan konsensusuppfattningen beräknas som en $k$ -term metalog i sluten form, där a $\displaystyle {\ fetsymbol {a}}}$ -koefficienter för konsensusmetallogen är helt enkelt ett viktat medelvärde av de individuella experternas. Detta resultat följer av Vincentization , där konsensuskvantilfunktionen är ett viktat medelvärde av individuella kvantilfunktioner.

Bayesiansk uppdatering i stängd form

I en klassisk artikel visar Howard (1970) hur beta-binomialfördelningen kan användas för att uppdatera, enligt Bayes regel i sluten form, osäkerheten över långtidsfrekvensen $\phi$ för en myntkastning som kommer upp "huvuden" i ljuset av nya myntkastningsdata. Däremot, om osäkerheten av intresse som ska uppdateras inte definieras av en skalär sannolikhet över en diskret händelse (som resultatet av ett myntkast) utan av en sannolikhetstäthetsfunktion över en kontinuerlig variabel, kan metalog Bayesian uppdatering användas. Under vissa förhållanden kan metalog-kvantilparametrar och ${\boldsymbol {a}}$ -koefficienter uppdateras i sluten form i ljuset av nya data enligt Bayes regel .

Ansökningar

För 3 474 steelhead-öringar som fångats och släppts ut på Babine River i British Columbia under 2006-2010, passade empiriska viktdata (histogram) och 10-term log metalog PDF (blå kurva) till dessa data med minsta kvadrater.

På grund av deras flexibilitet i form och gränser, kan metalogs användas för att representera empiriska eller andra data i praktiskt taget alla områden av mänsklig strävan.

• Astronomi . Metalogs användes för att bedöma riskerna för asteroidpåverkan.
• Cybersäkerhet . Metalogs användes vid riskbedömning av cybersäkerhet.
• Framkalla och kombinera expertutlåtanden . Statistics Canada fick fram expertutlåtanden om framtida kanadensiska fertilitetstal från 18 experter, vilket inkluderade användningen av kalkylbladsbaserad realtids-PDF-feedback baserad på fem-terms metalogs. De enskilda expertutlåtandena viktades sedan och kombinerades till en övergripande metalogbaserad prognos.
• Empirisk datautforskning och visualisering . Inom fiskbiologi passade en 10-terms log metalog-fördelning (avgränsad nedan vid 0) till vikten av 3 474 steelhead-öringar som fångats och släppts ut på Babine River i British Columbia under 2006–2010. Bimodaliteten i den resulterande utbredningen har tillskrivits närvaron av både förstagångs- och andragångslek i floden, av vilka de senare tenderar att väga mer.
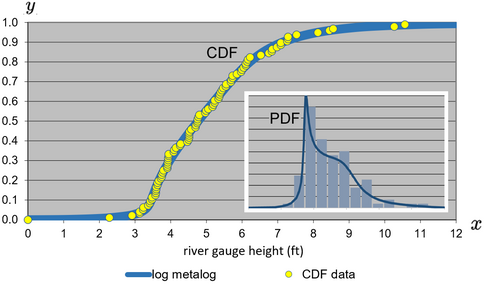
• Hydrologi . En 10-terms semi-bounded metalog användes för att modellera sannolikhetsfördelningen av årliga flodspårhöjder.
• Oljefältsproduktion . Semi-bounded SPT metalogs användes för att analysera fördomar i projektioner av oljefältsproduktion jämfört med observerad produktion i efterhand.
• Portföljförvaltning . SPT metalogs har använts för att modellera kommersiellt värde för nya produkter och produktportföljer.
• Simuleringsingångsfördelningar . För att stödja ett anbudsbeslut representerades osäkerheten om det framtida värdet av var och en av 259 finansiella tillgångar som en SPT-metallog. En simulering av det totala portföljvärdet visade sig ge mer realistiska resultat än en motsvarande simulering baserad på diskreta låga, median- och höga värden för varje tillgång.
• Simuleringsutgångsfördelningar . Metalogs har också använts för att anpassa utdata från simuleringar för att representera dessa utdata som kontinuerliga distributioner i sluten form (både CDF och PDF). Används på detta sätt är de vanligtvis mer stabila och jämnare än histogram.
• Summor av lognormaler . Metalogs möjliggör en representation i sluten form av kända distributioner vars CDF:er inte har något uttryck i sluten form. Keelin et al. (2019) tillämpar detta på summan av oberoende identiskt fördelade lognormalfördelningar, där kvantiler av summan kan bestämmas genom ett stort antal simuleringar. Nio sådana kvantiler används för att parametrisera en semi-bounded metalogdistribution som går igenom var och en av dessa nio kvantiler exakt. Kvantilparametrar lagras i en tabell, som sedan kan interpoleras för att ge mellanliggande värden; dessa värden är garanterat genomförbara av konvexitetsegenskapen ovan.

Metalog panel för stålhuvudviktsdata

Välj antal termer

För en given applikation och datamängd beror valet av antalet metalogtermer $k$ på sammanhanget och kan kräva bedömning. För expertinlärning räcker vanligtvis tre till fem termer. För datautforskning och matchning av andra sannolikhetsfördelningar som summan av lognormaler räcker det vanligtvis med åtta till 12 termer. En metalog-panel, som visar metalog-PDF-filerna som motsvarar olika antal termer $k$ för en given datamängd, kan hjälpa denna bedömning. Till exempel, i metalog-panelen med stålhuvudvikt, är användning av mindre än sju termer utan tvekan underpassad data genom att dölja datas inneboende bimodalitet. Att använda mer än 11 ​​termer är onödigt och kan i princip överpassa data. Fallet med 16 termer är omöjligt för denna datauppsättning, vilket indikeras av den tomma cellen i metalogpanelen. Andra verktyg (som regularisering , Akaike-informationskriterium och Bayesianskt informationskriterium ) kan också vara användbara. Till exempel, när den tillämpas på stålhuvudviktsdata, identifierar AIC-rankningen av metalogfördelningar från 2-16 termer tillsammans med ett brett utbud av klassiska distributioner den 11-termiga logmetallogen som den bästa passformen till dessa data. En liknande BIC-rankning identifierar 10-term log metalogen som den bästa passformen. Keelin (2016) ger ytterligare perspektiv på distributionsvalet inom metalogfamiljen.

Relaterade distributioner

Metalogfördelningarna tillhör gruppen av fördelningar som definieras i termer av kvantilfunktionen, som inkluderar de kvantilparameteriserade fördelningarna , Tukey lambda-fördelningen , dess generalisering, GLD, Govindarajulu-fördelningen och andra. Följande distributioner ingår i metalogfamiljen:

• Den logistiska fördelningen är ett specialfall av den obegränsade metalogen där $a_{i}=0$ för alla $i>2$ .
• Den enhetliga fördelningen är ett specialfall av: 1) den obegränsade metalogen där $k\geq 4$ , $a_{1}=0,5$ , $a_ {4}=1$ och $a_{i}=0$ annars; och 2) den avgränsade metalogen där $k\geq 2$ , $b_{l}=0$ , $b_{u}=1$ , $a_{2}=1$ och $a_{i}=0$ annars.
• Log -logistikfördelningen , även känd som Fisk-fördelningen inom ekonomi, är ett specialfall av stockmetallogen där $b_{l}=0$ och $a_{i}= 0$ för alla $i>2$ .
• Den log-likformiga fördelningen är ett specialfall av logmetalog där $k\geq 4$ , ${\displaystyle a_{1}=0.5} ,$ a $\displaystyle a_{ 4}=1}$ och $a_{i}=0$ annars.
• Logit-logistic distribution är ett specialfall av logit metalog där $a_{i}=0$ för alla $i>2$ .

programvara

Fritt tillgängliga mjukvaruverktyg kan användas för att arbeta med metalog-distributioner:

• Excel-arbetsböcker. Genom att klistra in eller skriva in CDF-data, visas metalogs (med val av gränser) omedelbart.
  • SPT metalogs arbetsbok beräknar 2–3 term metalogs bestämt av tre $(x_{i},y_{i})$ CDF-data.
  • Metalogs arbetsbok beräknar 2–16 termer metalogs (inklusive metalog panel) bestämt av 2-10 000 $(x_{i},y_{i})$ CDF-data.
  • ELD (lika troliga data) Metalog-arbetsböcker beräknar 2–16 termmetaloger bestämt av 2–10 000 $(x_{i})$ CDF-data, där $y_{i}$ s och metalog panel beräknas automatiskt.
• R. rmetalog (på Complehensive R Archive Network, CRAN ) .
• Pytonorm. Pymetalog återspeglar nära R-paketet. Metalogistic drar fördel av SciPy -plattformen.
• Webbläsare . MakeDistribution.com underlättar experiment med metalogs parametriserade av flera CDF-datapunkter. SPT metalog-kalkylatorn, metalog-kalkylatorn och ELD metalog-kalkylatorn är onlineversioner av Excel-arbetsböckerna.
• SIPmath Modeler Tools stöder metalog-distributioner i ett Excel-tillägg för simulering.
• Luminas programvara Analytica Free 101 för modellering och hjälp med svåra beslut.
• BayesFusions Metalog Builder möjliggör interaktiv uppbyggnad av metalogdistributioner. BayesFusions GeNIe (akademisk version av programvaran är gratis för akademisk forskning och undervisning) implementerar metalogdistributionerna.

Kommersiellt tillgängliga paket stöder också användningen av metalogdistributioner:

• FrontLine Solvers: Analytic Solver, RASON och Solver SDK, programvara för optimering. Anpassar automatiskt användardata till hela spektrumet av (avgränsade och obegränsade, multi-term) metalog-distributioner och ger möjlighet att jämföra metalog-distributioner med klassiska distributioner baserat på användarvalda godhetskriterier.
• Lone Star Analysis: TruNavigator och AnalyticsOS programvara för prediktiv och preskriptiv analys.

externa länkar

• Metalog Distributions webbplats, www.metalogs.org
• Metalog Distributions YouTube-kanal, utbildningsvideor