Kontinuerlig Bernoulli-distribution

Ej att förväxla med Bernoulli-distribution .

Kontinuerlig Bernoulli-distribution

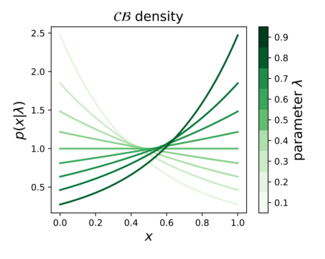
Sannolikhetstäthetsfunktion
Notation	${\mathcal {CB}}(\lambda )$
Parametrar	$\lambda \in (0,1)$
Stöd	$x\in [0,1]$
PDF	$C(\lambda )\lambda ^{x}(1-\lambda )^{1-x}\!$ där $C(\lambda )={\begin{cases}2&{\text{if }}\lambda ={\ frac {1}{2}}\\{\frac {2\tanh ^{-1}(1-2\lambda )}{1-2\lambda }}&{\text{ annars}}\end{case }}$
CDF	${\begin{cases}x&{\text{ if }}\lambda ={\frac { 1}{2}}\\{\frac {\lambda ^{x}(1-\lambda )^{1-x}+\lambda -1}{2\lambda -1}}&{\text{ annars }}\end{cases}}\!$
Betyda	$\operatorname {E} [X]={\begin{cases }{\frac {1}{2}}&{\text{ if }}\lambda ={\frac {1}{2}}\\{\frac {\lambda }{2\lambda -1}}+ {\frac {1}{2\tanh ^{-1}(1-2\lambda )}}&{\text{ annars}}\end{case}}\!$
Variation	$\operatornamn { var} [X]={\begin{cases}{\frac {1}{12}}&{\text{ if }}\lambda ={\frac {1}{2}}\\{\frac {( 1-\lambda )\lambda }{(1-2\lambda )^{2}}}+{\frac {1}{(2\tanh ^{-1}(1-2\lambda ))^{2 }}}&{\text{ annars}}\end{cases}}\!$

Inom sannolikhetsteori , statistik och maskininlärning $\lambda \in (0,1)$ den kontinuerliga Bernoulli-fördelningen en familj av kontinuerliga sannolikhetsfördelningar parametriserade av en enda formparameter , definierad på enhetsintervall $x\in [0,1]$ , av:

$p(x|\lambda )\propto \lambda ^{x}(1-\lambda )^{1-x}.$

Den kontinuerliga Bernoulli-distributionen uppstår i djupinlärning och datorseende , speciellt i samband med variationsautokodare , för modellering av pixelintensiteten hos naturliga bilder. Som sådan definierar den en korrekt probabilistisk motsvarighet för den vanligen använda binära $[0,1]$ , som ofta tillämpas på kontinuerliga, -värderade data. Denna praxis går ut på att ignorera normaliseringskonstanten för den kontinuerliga Bernoulli-fördelningen, eftersom den binära korsentropiförlusten endast definierar en sann log-sannolikhet för diskreta, { , $displaystyle \{0,1\}}$ -värderade data.

Den kontinuerliga Bernoulli definierar också en exponentiell familj av distributioner. Om du skriver $\eta =\log \left(\lambda /(1-\lambda )\right)$ för den naturliga parametern kan densiteten skrivas om i kanonisk form: $p(x|\eta )\propto \exp(\eta x)$ .

Relaterade distributioner

Bernoulli distribution

Den kontinuerliga Bernoulli kan ses som en kontinuerlig relaxation av Bernoulli-fördelningen , som definieras på den diskreta mängden $\{0,1\}$ , av sannolikhetsmassfunktionen

$p(x)=p^{x}(1-p)^{1-x},$

där $p$ är en skalär parameter mellan 0 och 1. Att tillämpa samma funktionella form på det kontinuerliga intervallet $[0,1]$ resulterar i den kontinuerliga Bernoullis sannolikhetstäthetsfunktion , upp till en normaliserande konstant.

Betadistribution

Betafördelningen har densitetsfunktionen :

$p(x)\propto x^{\alpha -1}(1-x)^{\beta -1},$

som kan skrivas om som:

$p(x)\propto x_{1}^{\alpha _{1}-1}x_{2}^{\alpha _{2}-1},$

där $\alpha _{1},\alpha _{2}$ är positiva skalära parametrar och $(x_{1},x_{2})$ representerar en godtycklig punkt inuti 1- simplexet , $\Delta ^{1}=\ {(x_{1},x_{2}):x_{1}>0,x_{2}>0,x_{1}+x_{2}=1\}$ . Genom att byta roll för parametern och argumentet i denna densitetsfunktion får vi:

$p(x)\propto \alpha _{1}^{x_{1}}\alpha _{2}^{x_{2}}.$

Denna familj är endast identifierbar upp till den linjära begränsningen ${\displaystyle \alpha _{1}+\alpha _{2}=1} ,$ varifrån vi får:

$p(x)\propto \lambda ^{x_{1}}(1-\lambda )^{x_{2}},$

motsvarande exakt den kontinuerliga Bernoulli-densiteten.

Exponentiell fördelning

En exponentiell fördelning begränsad till enhetsintervallet är ekvivalent med en kontinuerlig Bernoulli-fördelning med lämplig parameter.

Kontinuerlig kategorisk fördelning

Den multivariata generaliseringen av den kontinuerliga Bernoulli kallas den kontinuerliga-kategoriska.