Triangulär fördelning

Triangulär

Sannolikhetstäthetsfunktion
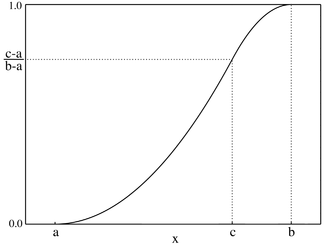
Kumulativ fördelningsfunktion
Parametrar	$a:~a\in (-\infty ,\infty )$$b:~a<b\,$$c:~a\leq c\leq b\,$
Stöd	$a\leq x\leq b\!$
PDF	${\begin{cases}0&{\text{för }}x<a,\\{\frac {2(xa)}{(ba)(ca)}}&{\text{för }}a \leq x<c,\\[4pt]{\frac {2}{ba}}&{\text{för }}x=c,\\[4pt]{\frac {2(bx)}{(ba )(bc)}}&{\text{för }}c<x\leq b,\\[4pt]0&{\text{för }}b<x.\end{cases}}$
CDF	${\begin{cases}0&{\text{för }}x\leq a,\\[2pt]{\frac {(xa)^{2}}{(ba)(ca)}}&{ \text{för }}a<x\leq c,\\[4pt]1-{\frac {(bx)^{2}}{(ba)(bc)}}&{\text{för }}c <x<b,\\[4pt]1&{\text{för }}b\leq x.\end{cases}}$
Betyda	${\frac {a+b+c}{3}}$
Median	${\begin{cases}a+{\sqrt {\frac {(ba)(ca)}{2}}}&{\text{för }}c\geq {\frac {a+b}{2 }},\\[6pt]b-{\sqrt {\frac {(ba)(bc)}{2}}}&{\text{för }}c\leq {\frac {a+b}{2 }}.\end{cases}}$
Läge	$c\,$
Variation	${\frac {a^{2}+b^{2}+c^{2}-ab-ac-bc}{ 18}}$
Skevhet	${\frac {{\sqrt {2}}(a\!+\!b\!-\!2c)(2a\!-\!b\!-\!c)(a\!-\!2b\ !+\!c)}{5(a^{2}\!+\!b^{2}\!+\!c^{2}\!-\!ab\!-\!ac\!- \!bc)^{\frac {3}{2}}}}$
Ex. kurtosis	$-{\frac {3}{5}}$
Entropi	${\frac {1}{2}}+\ln \left({\frac {ba}{2}}\right)$
MGF	$2{\ frac {(b\!-\!c)e^{at}\!-\!(b\!-\!a)e^{ct}\!+\!(c\!-\!a)e ^{bt}}{(ba)(ca)(bc)t^{2}}}$
CF	${\ displaystyle -2{\frac {(b\!-\!c)e^{iat}\!-\!(b\!-\!a)e^{ict}\!+\!(c\!- \!a)e^{ibt}}{(ba)(ca)(bc)t^{2}}}}$

Inom sannolikhetsteori och statistik är triangulärfördelningen en kontinuerlig sannolikhetsfördelning med undre gräns a , övre gräns b och mod c , där a < b och a ≤ c ≤ b .

Speciella fall

Läge på gränsen

Fördelningen förenklas när c = a eller c = b . Till exempel, om a = 0, b = 1 och c = 1, blir PDF: en och CDF :en:

$\left.{\begin{array}{rl}f(x)&=2x\\[8pt]F(x) )&=x^{2}\end{array}}\right\}{\text{ för }}0\leq x\leq 1$

${ \displaystyle {\begin{aligned}\operatörsnamn {E} (X)&={\frac {2}{3}}\\[8pt]\operatörsnamn {Var} (X)&={\frac {1}{ 18}}\end{aligned}}}$

Fördelning av den absoluta skillnaden mellan två enhetliga standardvariabler

Denna fördelning för a = 0, b = 1 och c = 0 är fördelningen av X = | X ₁ − X ₂ |, där X ₁ , X ₂ är två oberoende stokastiska variabler med enhetlig standardfördelning .

${\begin {aligned}f(x)&=2-2x{\text{ för }}0\leq x<1\\[6pt]F(x)&=2x-x^{2}{\text{ för }} 0\leq x<1\\[6pt]E(X)&={\frac {1}{3}}\\[6pt]\operatörsnamn {Var} (X)&={\frac {1}{18 }}\end{aligned}}$

Symmetrisk triangulär fördelning

Det symmetriska fallet uppstår när c = ( a + b ) / 2. I detta fall är en alternativ form av fördelningsfunktionen:

${\begin{aligned}f(x)&={\frac {(bc)-|cx|}{(bc)^{2}}}\\[6pt]\end {Justerat}}$

Fördelning av medelvärdet av två enhetliga standardvariabler

Denna fördelning för a = 0, b = 1 och c = 0,5—moden (dvs toppen) är exakt i mitten av intervallet—motsvarar fördelningen av medelvärdet av två enhetliga standardvariabler, det vill säga fördelningen av X = ( X ₁ + X ₂ ) / 2, där X ₁ , X ₂ är två oberoende slumpvariabler med enhetlig standardfördelning i [0, 1]. Det är fallet med Bates-fördelningen för två variabler.

$f(x)={\begin{cases}4x&{\text{for }}0 \leq x<{\frac {1}{2}}\\4(1-x)&{\text{för }}{\frac {1}{2}}\leq x\leq 1\end{case }}$

$F(x)={\begin{cases} 2x^{2}&{\text{för }}0\leq x<{\frac {1}{2}}\\2x^{2}-(2x-1)^{2}&{\text{ för }}{\frac {1}{2}}\leq x\leq 1\end{cases}}$

${\begin{aligned} E(X)&={\frac {1}{2}}\\[6pt]\operatörsnamn {Var} (X)&={\frac {1}{24}}\end{aligned}}$

Genererar triangulärt fördelade slumpmässiga variationer

Givet en slumpmässig variant U dragen från den enhetliga fördelningen i intervallet (0, 1), då variaten

$X={\begin{cases}a+{\sqrt {U(ba)(ca)}}&{\text{ för }}0<U<F(c)\\&\\b-{\ sqrt {(1-U)(ba)(bc)}}&{\text{ för }}F(c)\leq U<1\end{cases}}$

där $F(c)=(ca)/(ba)$ , har en triangulär fördelning med parametrarna $a,b$ och $c$ . Detta kan erhållas från den kumulativa fördelningsfunktionen.

Användning av distributionen

Se även: Trepunktsuppskattning

Triangulärfördelningen används vanligtvis som en subjektiv beskrivning av en population för vilken det bara finns begränsade urvalsdata, och särskilt i de fall där förhållandet mellan variabler är känt men data är knapphändig (möjligen på grund av den höga kostnaden för insamling). Den bygger på kunskap om minimum och maximum och en "inspirerad gissning" om det modala värdet. Av dessa skäl har triangelfördelningen kallats en "kunskapsbrist"-fördelning.

Affärssimuleringar

Triangulärfördelningen används därför ofta i affärsbeslut , särskilt i simuleringar . I allmänhet, när inte mycket är känt om fördelningen av ett resultat (säg bara dess minsta och största värden), är det möjligt att använda den enhetliga fördelningen . Men om det mest sannolika utfallet också är känt, så kan utfallet simuleras med en triangulär fördelning. Se till exempel under corporate finance .

Projektledning

Den triangulära distributionen, tillsammans med PERT-distributionen , används också i stor utsträckning inom projektledning (som en input till PERT och därmed kritisk vägmetod (CPM)) för att modellera händelser som äger rum inom ett intervall som definieras av ett minimum- och maximivärde.

Ljudvibrering

Den symmetriska triangulära fördelningen används vanligen vid ljudvibrering , där den kallas TPDF (triangular probability density function).

Strålformning

Den triangulära fördelningen har en tillämpning på strålformning och mönstersyntes.

Se även

• Trapetsfördelning
• Thomas Simpson
• Trepunktsuppskattning
• Femsiffrig sammanfattning
• Sjusiffrig sammanfattning
• Triangulär funktion
• Central limit theorem — Triangelfördelningen uppstår ofta som ett resultat av att två enhetliga slumpvariabler adderas. Med andra ord är triangelfördelningen ofta (inte alltid) resultatet av den första iterationen av summeringsprocessen för centralgränssatsen (dvs ${\textstil n=2} )$ . I denna mening kan triangelfördelningen ibland förekomma naturligt. Om denna process att summera fler slumpvariabler fortsätter (dvs ${\textstyle n\geq 3} )$ , så kommer fördelningen att bli allt mer klockformad.
• Irwin–Hall-fördelning — Att använda en Irwin–Hall-fördelning är ett enkelt sätt att generera en triangelfördelning.
• Bates-fördelning — Liknar Irwin-Hall-fördelningen, men med värdena skalade tillbaka till intervallet 0 till 1. Användbar för beräkning av en triangelfördelning som sedan kan skalas om och skiftas för att skapa andra triangelfördelningar utanför intervallet 0 till 1.

externa länkar

• Weisstein, Eric W. "Triangulär distribution" . MathWorld .
• Triangle Distribution , decisionsciences.org
• Triangular Distribution , brighton-webs.co.uk
• Bevis för variansen av triangulär distribution, math.stackexchange.com