Logit-normalfördelning

Logit-normal

Sannolikhetstäthetsfunktion
Kumulativ fördelningsfunktion
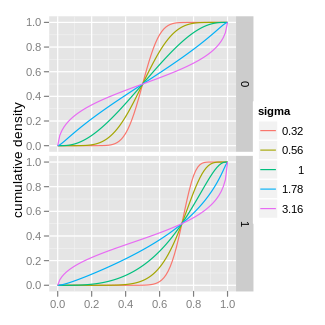
Notation	$P({\mathcal {N}}(\mu ,\,\sigma ^{2}))$
Parametrar	σ 2 > 0 — kvadratisk skala (real), μ ∈ R — plats
Stöd	x ∈ (0, 1)
PDF	${\frac {1}{\sigma {\sqrt {2\pi }}}}\ ,e^{-{\frac {(\operatörsnamn {logit} (x)-\mu )^{2}}{2\sigma ^{2}}}}{\frac {1}{x(1-x )}}$
CDF	${\frac {1}{2}}{\Big [}1+\operatörsnamn {erf} {\Big (} {\frac {\operatörsnamn {logit} (x)-\mu }{\sqrt {2\sigma ^{2}}}}{\Big )}{\Big ]}$
Betyda	ingen analytisk lösning
Median	$P(\mu )\,$
Läge	ingen analytisk lösning
Variation	ingen analytisk lösning
MGF	ingen analytisk lösning

I sannolikhetsteorin är en logit-normalfördelning en sannolikhetsfördelning av en slumpvariabel vars logit har en normalfördelning . Om Y är en slumpvariabel med en normalfördelning och t är den logistiska standardfunktionen , så har X = t ( Y ) en logit-normalfördelning; på samma sätt, om X är logit-normalfördelad, då är Y = logit ( X )= log ( X /(1- X )) normalfördelad. Det är också känt som den logistiska normalfördelningen , som ofta hänvisar till en multinomial logitversion (t.ex.).

En variabel kan modelleras som logit-normal om det är en proportion, som begränsas av noll och ett, och där värden på noll och ett aldrig förekommer.

Karakterisering

Sannolikhetstäthetsfunktion

Sannolikhetstäthetsfunktionen (PDF) för en logit-normalfördelning, för 0 < x < 1, är:

$f_{X}(x;\mu ,\ sigma )={\frac {1}{\sigma {\sqrt {2\pi }}}}\,{\frac {1}{x(1-x)}}\,e^{-{\frac { (\operatörsnamn {logit} (x)-\mu )^{2}}{2\sigma ^{2}}}}$

där μ och σ är medelvärdet och standardavvikelsen för variabelns logit (definitivt är variabelns logit normalfördelad).

Densiteten som erhålls genom att ändra tecknet för μ är symmetrisk, eftersom den är lika med f(1-x;- μ , σ ), vilket skiftar läget till andra sidan av 0,5 (mittpunkten av (0,1) intervallet ).

Plott av Logitnormal PDF för olika kombinationer av μ (facetter) och σ (färger)

Ögonblick

Momenten för logit-normalfördelningen har ingen analytisk lösning. Momenten kan uppskattas genom numerisk integration , men numerisk integration kan vara oöverkomlig när värdena för ${\textstyle \mu ,\sigma ^{2}}$ är sådana att densitetsfunktionen divergerar till oändligt vid ändpunkterna noll och en. Ett alternativ är att använda observationen att logit-normalen är en transformation av en normal slumpvariabel. Detta gör att vi kan approximera det $n$ -th momentet via följande kvasi Monte Carlo-uppskattning $E[X^{n}]\approx {\frac {1}{K-1}}\summa _{i=1}^{K-1}\left( P\left(\Phi _{\mu ,\sigma ^{2}}^{-1}(i/K)\right)\right)^{n},$

där ${\textstyle P}$ är standardlogistikfunktionen, och ${\textstyle \Phi _{\mu ,\sigma ^{2}}^{-1}}$ är den inversa kumulativa fördelningsfunktionen av en normalfördelning med medelvärde och varians ${\textstyle \mu ,\sigma ^{2}}$ .

Läge eller lägen

När derivatan av densiteten är lika med 0 så uppfyller läget för moden x följande ekvation:

$\operatörsnamn {logit} (x)=\sigma ^{2}(2x-1)+\mu .$

För vissa värden på parametrarna finns två lösningar, dvs fördelningen är bimodal .

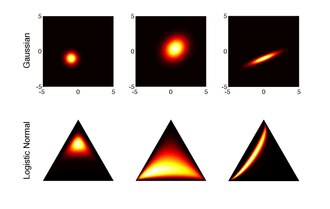
Multivariat generalisering

Den logistiska normalfördelningen är en generalisering av logit-normalfördelningen till D-dimensionella sannolikhetsvektorer genom att ta en logistisk transformation av en multivariat normalfördelning.

Sannolikhetstäthetsfunktion

Sannolikhetstäthetsfunktionen är :

$f_{X}(\mathbf {x} ;{\boldsymbol {\mu }},{\boldsymbol {\Sigma }})={\frac {1}{|(2\pi )^{D- 1}{\boldsymbol {\Sigma }}|^{\frac {1}{2}}}}\,{\frac {1}{\prod \limits _{i=1}^{D}x_{i }}}\,e^{-{\frac {1}{2}}\left\{\log \left({\frac {\mathbf {x} _{-D}}{x_{D}}} \right)-{\boldsymbol {\mu }}\right\}^{\top }{\boldsymbol {\Sigma }}^{-1}\left\{\log \left({\frac {\mathbf { x} _{-D}}{x_{D}}}\right)-{\boldsymbol {\mu }}\right\}}\quad ,\quad \mathbf {x} \in {\mathcal {S} }^{D}\;\;,$

där $\mathbf {x} _{-D}$ anger en vektor av de första (D-1) komponenterna av $\mathbf {x}$ och ${\mathcal {S}}^{D}$ betecknar simplexet för D-dimensionella sannolikhetsvektorer. Detta följer av att tillämpa den additiva logistiska transformationen för att kartlägga en multivariat normal stokastisk variabel ${\displaystyle \mathbf {y} \sim {\mathcal {N}}\left( {\boldsymbol {\mu }},{\boldsymbol {\Sigma }}\right)\;,\;\mathbf {y} \in \mathbb {R} ^{D-1}} till simplex$ :

$\mathbf {x} =\left[{\frac {e^{y_{1}}}{1+\sum _{i=1}^{D-1}e^{y_ {i}}}},\dots ,{\frac {e^{y_{D-1}}}{1+\sum _{i=1}^{D-1}e^{y_{i}} }},{\frac {1}{1+\sum _{i=1}^{D-1}e^{y_{i}}}}\right]^{\top }$

Gaussiska densitetsfunktioner och motsvarande logistiska normaldensitetsfunktioner efter logistisk transformation.

Den unika inversa mappningen ges av:

$\mathbf {y} =\left[\log \left({\frac {x_{1 }}{x_{D}}}\right),\dots ,\log \left({\frac {x_{D-1}}{x_{D}}}\right)\right]^{\top }$ .

Detta är fallet med en vektor x som sammanfattar komponenter till ett. I fallet med x med sigmoidala element, det vill säga när

$\mathbf {y} =\left[\log \left({\frac {x_ {1}}{1-x_{1}}}\right),\dots ,\log \left({\frac {x_{D}}{1-x_{D}}}\right)\right]^ {\topp }$

vi har

$f_{X}(\mathbf {x} ;{\boldsymbol {\mu }},{\boldsymbol {\Sigma }})={\frac {1}{|2\pi {\boldsymbol {\Sigma }}|^{\frac {1}{2}}}}\,{\frac {1}{\prod \limits _{i=1}^{D}\left(x_{i}(1-x_ {i})\right)}}\,e^{-{\frac {1}{2}}\left\{\log \left({\frac {\mathbf {x} }{1-\mathbf { x} }}\right)-{\boldsymbol {\mu }}\right\}^{\top }{\boldsymbol {\Sigma }}^{-1}\left\{\log \left({\frac {\mathbf {x} }{1-\mathbf {x} }}\right)-{\boldsymbol {\mu }}\right\}}$

där loggen och divisionen i argumentet tas elementmässigt. Detta beror på att transformationens jakobiska matris är diagonal med elementen ${\frac {1}{x_{i}(1-x_{i})}}$ .

Använd i statistisk analys

Den logistiska normalfördelningen är ett mer flexibelt alternativ till Dirichlet-fördelningen genom att den kan fånga korrelationer mellan komponenter i sannolikhetsvektorer. Det har också potential att förenkla statistiska analyser av sammansättningsdata genom att tillåta en att svara på frågor om log-förhållanden mellan komponenterna i datavektorerna. Man är ofta intresserad av kvoter snarare än absoluta komponentvärden.

Sannolikhetssimplexet är ett avgränsat utrymme, vilket gör standardtekniker som vanligtvis tillämpas på vektorer i $\mathbb {R} ^{n}$ mindre meningsfulla. Aitchison beskrev problemet med falska negativa korrelationer när man tillämpar sådana metoder direkt på enkla vektorer. Mappning av sammansättningsdata i ${\mathcal {S}}^{D}$ genom inversen av den additiva logistiska transformationen ger emellertid realvärderade data i $\mathbb {R} ^ {D-1}$ . Standardtekniker kan tillämpas på denna representation av data. Detta tillvägagångssätt motiverar användningen av den logistiska normalfördelningen, som alltså kan betraktas som "simplexens Gauss".

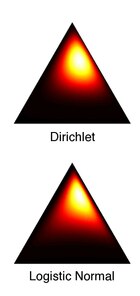
Förhållande till Dirichlet-distributionen

Logistisk normal approximation till Dirichlet distribution

Dirichlet och logistisk normalfördelning är aldrig exakt lika för val av parametrar . Aitchison beskrev emellertid en metod för att approximera en Dirichlet med en logistisk normal så att deras Kullback–Leibler divergens (KL) minimeras:

$K(p,q)=\int _{ {\mathcal {S}}^{D}}p\left(\mathbf {x} \mid {\boldsymbol {\alpha }}\right)\log \left({\frac {p\left(\mathbf { x} \mid {\boldsymbol {\alpha }}\right)}{q\left(\mathbf {x} \mid {\boldsymbol {\mu }},{\boldsymbol {\Sigma }}\right)}} \right)\,d\mathbf {x}$

Detta minimeras genom:

${\boldsymbol {\mu }}^{*}=\ mathbf {E} _{p}\left[\log \left({\frac {\mathbf {x} _{-D}}{x_{D}}}\right)\right]\quad ,\quad { \boldsymbol {\Sigma }}^{*}={\textbf {Var}}_{p}\left[\log \left({\frac {\mathbf {x} _{-D}}{x_{D }}}\eller hur]$

Med hjälp av momentegenskaper för Dirichlet-fördelningen kan lösningen skrivas i termer av funktionerna digamma $\psi$ och trigamma ${\displaystyle \psi '} :$

$\mu _{i}^{*}=\psi \left(\alpha _{i} \right)-\psi \left(\alpha _{D}\right)\quad ,\quad i=1,\ldots ,D-1$

$\Sigma _{ii}^{*}=\psi '\left(\alpha _{i}\right)+\psi '\left(\alpha _{D}\right)\quad ,\quad i=1,\ldots ,D-1$

$\Sigma _{ij}^{* }=\psi '\left(\alpha _{D}\right)\quad ,\quad i\neq j$

Denna uppskattning är särskilt korrekt för stora ${\boldsymbol {\alpha }}$ . I själva verket kan man visa att för ${\displaystyle \alpha _{i}\rightarrow \infty ,i=1,\ldots ,D} ,$ har vi att $p\left(\mathbf {x} \mid {\boldsymbol {\alpha }}\right)\högerpil q\left(\mathbf {x} \mid {\boldsymbol {\mu }}^{*},{\boldsymbol {\Sigma }}^{*}\right)$ .

Se även

• Betadistribution och Kumaraswamy-distribution , andra tvåparameterdistributioner på ett begränsat intervall med liknande former

Vidare läsning

• Frederic, P. & Lad, F. (2008) Two Moments of the Logitnormal Distribution. Kommunikation i statistik-simulering och beräkning . 37: 1263-1269
•    Mead, R. (1965). "En generaliserad logit-normal distribution". Biometri . 21 (3): 721–732. doi : 10.2307/2528553 . JSTOR 2528553 . PMID 5858101 .

externa länkar

• logitnorm-paket för R