Burr typ XII
Sannolikhetstäthetsfunktion
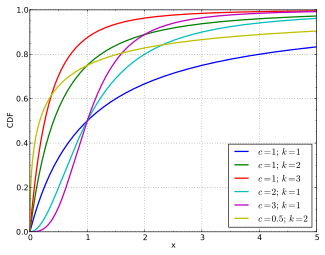
Kumulativ fördelningsfunktion
Parametrar
c >
0
{\displaystyle c>0\!}
k >
0
{\displaystyle k>0\!}
Stöd
x >
0
{\displaystyle x>0\!}
PDF
c k
x
c − 1
( 1 +
x
c
)
k + 1
{\displaystyle ck{\frac {x^{c-1}}{(1+x^{c})^{k+1}}}\ !}
CDF
1 −
(
1 +
x
c
)
− k
{\displaystyle 1-\left(1+x^{c}\right)^{-k}}
Betyda
μ
1
= k
B
( k − 1
/
c , 1 + 1
/
c )
{\displaystyle \mu _{1}=k\operatörsnamn {\mathrm {B} } (k-1/c,\,1+ 1/c)}
betafunktionen
Median
(
2
1 k
− 1
)
1 c
{\displaystyle \left(2^{\frac {1}{k}}-1\right)^{\frac {1}{c}}}
Läge
(
c − 1
k c + 1
)
1 c
{\displaystyle \left({\frac {c-1}{kc+1}}\right)^{\frac {1}{c}}}
Variation
−
μ
1
2
+
μ
2
{\displaystyle -\mu _{1}^{2}+\mu _{2}}
Skevhet
2
μ
1
3
− 3
μ
1
μ
2
+
μ
3
(
−
μ
1
2
+
μ
2
)
3
/
2
{\displaystyle {\frac {2\mu _{1}^{3}-3\mu _{1 }\mu _{2}+\mu _{3}}{\left(-\mu _{1}^{2}+\mu _{2}\right)^{3/2}}}}
Ex. kurtosis
− 3
μ
1
4
+ 6
μ
1
2
μ
2
− 4
μ
1
μ
3
+
μ
4
(
−
μ
1
2
+
μ
2
)
2
− 3
{\displaystyle {\frac {-3\mu _{1}^{ 4}+6\mu _{1}^{2}\mu _{2}-4\mu _{1}\mu _{3}+\mu _{4}}{\left(-\mu _ {1}^{2}+\mu _{2}\right)^{2}}}-3}
se )
μ
r
= k
B
(
c k − r
c
,
c + r
c
)
{ \displaystyle \mu _{r}=k\operatörsnamn {\mathrm {B} } \left({\frac {ck-r}{c}},\,{\frac {c+r}{c}}\ höger)}
CF
=
,
c ( −i t
)
k c
Γ ( k )
H
1 , 2
2
|
1
[
( −i t
)
c
_
_
( − k , 1 )
0
( , 1 ) , ( − k c , c )
]
, t ≠
0
{\displaystyle ={\frac {c(-it)^{kc}}{\Gamma (k)}}H_{ 1,2}^{2,1}\!\left[(-it)^{c}\left|{\begin{matris}(-k,1)\\(0,1),(-kc, c)\end{matrix}}\right.\right],t\neq 0}
= 1 , t =
0
{\displaystyle =1,t=0}
Γ
{\displaystyle \Gamma }
gammafunktionen och
H
{ \displaystyle H}
Fox H-funktionen .
Inom sannolikhetsteori , statistik och ekonometri är Burr Type XII-fördelningen eller helt enkelt Burr-fördelningen en kontinuerlig sannolikhetsfördelning för en icke-negativ stokastisk variabel . Det är också känt som Singh-Maddala-distributionen och är en av ett antal olika distributioner som ibland kallas "generaliserad log-logistisk distribution" . Det används oftast för att modellera hushållsinkomst , se till exempel: Hushållsinkomst i USA och jämför med magentafärgad graf till höger.
Burr (Typ XII)-fördelningen har sannolikhetstäthetsfunktion :
f ( x ; c , k )
= c k
x
c − 1
( 1 +
x
c
)
k + 1
f ( x ; c , k , λ )
=
c k
λ
(
x λ
)
c − 1
[
1 +
(
x ) λ
)
c
]
− k − 1
{\displaystyle {\begin{aligned}f(x;c,k)&=ck{\frac {x^{c-1}}{(1+x^{c}) ^{k+1}}}\\[6pt]f(x;c,k,\lambda )&={\frac {ck}{\lambda }}\left({\frac {x}{\lambda } }\right)^{c-1}\left[1+\left({\frac {x}{\lambda }}\right)^{c}\right]^{-k-1}\end{aligned }}}
och kumulativ distributionsfunktion :
F ( x ; c , k ) = 1 −
(
1 +
x
c
)
− k
{\displaystyle F(x;c,k)=1-\left(1+x^{c}\right)^{-k }}
F ( x ; c , k , λ ) = 1 −
[
1 +
(
x λ
)
c
]
− k
{\displaystyle F(x;c,k,\lambda )=1-\vänster[1+\vänster ({\frac {x}{\lambda }}\right)^{c}\right]^{-k}}
Relaterade distributioner
Burr Type XII-distributionen är en medlem av ett system med kontinuerliga distributioner som introducerades av Irving W. Burr (1942), som omfattar 12 distributioner. Dagum -fördelningen , även känd som den omvända Burr-fördelningen, är fördelningen av 1/ X , där X har Burr-fördelningen
Vidare läsning
externa länkar
Riktad
Degenererad och singular
Familjer













![{\displaystyle ={\frac {c(-it)^{kc}}{\Gamma (k)}}H_{1,2}^{2,1}\!\left[(-it)^{c}\left|{\begin{matrix}(-k,1)\\(0,1),(-kc,c)\end{matrix}}\right.\right],t\neq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d57864ffe50078a34292d9f949f09e0f47ab2b3)



![{\displaystyle {\begin{aligned}f(x;c,k)&=ck{\frac {x^{c-1}}{(1+x^{c})^{k+1}}}\\[6pt]f(x;c,k,\lambda )&={\frac {ck}{\lambda }}\left({\frac {x}{\lambda }}\right)^{c-1}\left[1+\left({\frac {x}{\lambda }}\right)^{c}\right]^{-k-1}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3c758cb4945e4a43a37fb66ad628b53ca8de40c)

![{\displaystyle F(x;c,k,\lambda )=1-\left[1+\left({\frac {x}{\lambda }}\right)^{c}\right]^{-k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00238e8a5ecdca4563db2344bfca37b93baee67f)