Gumbel distribution

Gumbel

Sannolikhetstäthetsfunktion
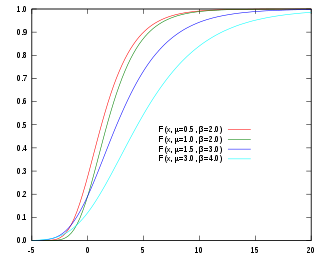
Kumulativ fördelningsfunktion
Notation	${\text{Gumbel}}(\mu ,\beta )$
Parametrar	$\mu ,$ plats ( verklig ) $\beta >0,$ skala (riktig)
Stöd	$x\in \mathbb {R}$
PDF	${\frac {1}{\beta }}e^{-(z+e^{-z})}$ där ${\ displaystyle z={\frac {x-\mu }{\beta }}}$
CDF	$e^{-e^{-(x-\mu )/\beta }}$
Betyda	$\mu +\beta \gamma$ där $\gamma$ är Euler–Mascheroni-konstanten
Median	$\mu -\beta \ln(\ln 2)$
Läge	$\mu$
Variation	${\frac {\pi ^{2}}{6}}\beta ^{2}$
Skevhet	${\frac {12{\sqrt {6}}\,\zeta (3)}{\pi ^{3}}}\ca 1.14$
Ex. kurtosis	${\frac {12}{5}}$
Entropi	$\ln(\beta )+\gamma +1$
MGF	$\Gamma (1-\beta t)e^{\mu t}$
CF	$\Gamma (1-i\beta t)e^{i\mu t}$

I sannolikhetsteori och statistik används Gumbel-fördelningen (även känd som typ-I-generaliserad extremvärdesfördelning) för att modellera fördelningen av maximum (eller minimum) av ett antal urval av olika distributioner .

Denna fördelning kan användas för att representera fördelningen av maxnivån i en flod under ett visst år om det fanns en lista med maximivärden för de senaste tio åren. Det är användbart för att förutsäga risken att en extrem jordbävning, översvämning eller annan naturkatastrof kommer att inträffa. Den potentiella tillämpbarheten av Gumbel-fördelningen för att representera fördelningen av maxima relaterar till extremvärdesteori , vilket indikerar att det sannolikt kommer att vara användbart om fördelningen av de underliggande provdata är av normal eller exponentiell typ. Den här artikeln använder Gumbel-fördelningen för att modellera fördelningen av det maximala värdet . För att modellera minimivärdet, använd det negativa av de ursprungliga värdena.

Gumbel-fördelningen är ett särskilt fall av den generaliserade extremvärdesfördelningen (även känd som Fisher-Tippett-fördelningen). Det är också känt som log- Weibull-fördelningen och den dubbla exponentialfördelningen (en term som ibland används för att referera till Laplace-fördelningen ). Det är relaterat till Gompertz-fördelningen : när dess densitet först reflekteras kring origo och sedan begränsas till den positiva halvlinjen, erhålls en Gompertz-funktion.

I den latenta variabelformuleringen av multinomial logit -modellen - vanlig i teorin om diskret val - följer felen hos de latenta variablerna en Gumbel-fördelning. Detta är användbart eftersom skillnaden mellan två Gumbel-fördelade slumpvariabler har en logistisk fördelning .

Gumbeldistributionen är uppkallad efter Emil Julius Gumbel (1891–1966), baserat på hans originalhandlingar som beskriver distributionen.

Definitioner

Den kumulativa fördelningsfunktionen för Gumbel-distributionen är

$F(x;\mu ,\beta )=e^{-e^{-(x-\mu )/\beta }}.\,$

Standard Gumbel distribution

Standard Gumbel-fördelningen är fallet där $\mu =0$ och $\beta =1$ med kumulativ fördelningsfunktion

$F(x)=e^{-e^{(-x)}}\,$

och sannolikhetstäthetsfunktion

$f(x)=e^{-(x+e^{-x})}.$

I det här fallet är läget 0, medianen är $-\ln(\ln(2))\approx 0,3665$ , medelvärdet är $\gamma \approx 0,5772$ ( Euler–Mascheroni-konstanten ), och standardavvikelsen är $\pi /{\sqrt {6}}\approx 1,2825.$

Kumulanterna, för n>1, ges av

$\kappa _{n}=(n-1)!\zeta (n).$

Egenskaper

Läget är μ, medan medianen är $\mu -\beta \ln \left(\ln 2\right),$ och medelvärdet ges av

$\operatörsnamn {E} (X)=\mu +\gamma \beta$ ,

där $\gamma$ är Euler-Mascheroni-konstanten .

Standardavvikelsen $\sigma$ är $\beta \pi /{\sqrt {6}}$ alltså $\beta =\sigma {\sqrt {6}}/\pi \approx 0,78\sigma .$

I läget, där ${\displaystyle x=\mu } ,$ blir värdet på $F(x;\mu ,\beta )$${\ displaystyle e^{-1}\approx 0.37} ,$ oavsett värdet på $\beta .$

Relaterade distributioner

• Om $X$ har en Gumbel-fördelning, så har den villkorliga fördelningen av Y=−X givet att Y är positiv, eller motsvarande givet att X är negativ, en Gompertz-fördelning . CDF G för Y är relaterad till F , CDF för X , med formeln $G(y)=P(Y\leq y)=P(X\geq -y|X\leq 0)=(F(0)-F(-y))/F (0)$ för y >0. Följaktligen är densiteterna relaterade till $g(y)=f(-y)/F(0)$ : Gompertz-densiteten är proportionell mot en reflekterad Gumbel densitet, begränsad till den positiva halvlinjen.
• Om X är en exponentiellt fördelad variabel med medelvärde 1, så har −log( X ) en standard Gumbelfördelning.
• Om $X\sim \mathrm {Gumbel} (\alpha _{X},\beta )$ och $Y\sim \mathrm {Gumbel} (\alpha _{Y},\beta )$ är oberoende, då ${\displaystyle XY\sim \mathrm {Logistisk} (\alpha _{X}-\alpha _{Y},\beta )\,} ($ se Logistisk distribution ).
• Om $X,Y\sim \mathrm {Gumbel} (\alpha ,\beta )$ är oberoende, då är $X+Y\nsim \mathrm {Logistic} (2\alpha ,\beta )$ . Observera att $E(X+Y)=2\alpha + 2\beta \gamma \neq 2\alpha =E\left(\mathrm {Logistic} (2\alpha ,\beta )\right)$ . Mer allmänt kan fördelningen av linjära kombinationer av oberoende Gumbel-slumpvariabler approximeras med GNIG- och GIG-fördelningar.

Teori relaterad till den generaliserade multivariata log-gamma-fördelningen ger en multivariat version av Gumbel-fördelningen.

Förekomst och tillämpningar

Distributionsanpassning med konfidensband av en kumulativ Gumbel-fördelning till maximala endagsregn i oktober.

Gumbel har visat att det maximala värdet (eller sista ordningens statistik ) i ett urval av slumpvariabler efter en exponentiell fördelning minus den naturliga logaritmen för urvalsstorleken närmar sig Gumbel-fördelningen när urvalsstorleken ökar.

Konkret, låt $\rho (x)=e^{-x}$ vara sannolikhetsfördelningen av $x$ och ${ \displaystyle Q(x)=1-e^{-x}}$ dess kumulativa fördelning. Då är det maximala värdet av $N$ realisationer av $x$ mindre än $X$ om och endast om alla realisationer är mindre än $X$ . Så den kumulativa fördelningen av det maximala värdet ${\tilde {x}}$ uppfyller

$P({\tilde {x}}-\log(N)\leq X)=P({\tilde {x}}\leq X+\log(N))=[Q(X+\log( N))]^{N}=\left(1-{\frac {e^{-X}}{N}}\höger)^{N}$ ,

och för stora $N}$$e^{-e^{(-X)}}.$ konvergerar den högra sidan till

Inom hydrologi används därför Gumbel-fördelningen för att analysera sådana variabler som månatliga och årliga maximivärden för daglig nederbörd och flodutsläppsvolymer, och även för att beskriva torka.

Gumbel har också visat att estimatorn r ⁄ ( n +1) för sannolikheten för en händelse — där r är rangnumret för det observerade värdet i dataserien och n är det totala antalet observationer — är en opartisk estimator av kumulativ sannolikhet kring fördelningsläget . Därför används denna estimator ofta som en plottningsposition .

I talteorin approximerar Gumbel-fördelningen antalet termer i en slumpmässig partition av ett heltal såväl som de trendjusterade storlekarna för maximala primtalsluckor och maximala gap mellan primtalskonstellationer .

Gumbel omparametriseringstrick

I maskininlärning används ibland Gumbel-distributionen för att generera prover från den kategoriska distributionen . Denna teknik kallas "Gumbel-max-trick" och är ett speciellt exempel på "reparametriseringstrick".

I detalj, låt $(\pi _{1},...,\pi _{n})$ vara icke-negativ, och inte alla noll, och låt $g_{1},...,g_{n}$ vara oberoende prover av Gumbel(0, 1), sedan genom rutinintegrering,

$$Pr(j=\arg \max _{i}(g_{i}+\log \ pi _{i}))={\frac {\pi _{j}}{\sum _{i}\pi _{i}}}$$

Det vill säga, $\arg \max _{i}(g_{i}+\log \pi _{ i})\sim {\text{Kategorisk}}\left({\frac {\pi _{j}}{\sum _{i}\pi _{i}}}\right)_{j}$

På motsvarande sätt, givet valfri ${\displaystyle x_{1},...,x_{n}\in \mathbb {R} } ,$ vi kan sampla från dess Boltzmann-fördelning genom att

$$_{i}(g_{i}+x_{i }))={\frac {e^{x_{j}}}{\sum _{i}e^{x_{i}}}}}$$

Relaterade ekvationer inkluderar:

• Om $x\sim Exp(\lambda )$ , då $(-\ln x-\gamma )\sim {\text{Gumbel}}(-\gamma +\ln \lambda ,1)$ .
• $\arg \max _{i}(g_{i}+\log \pi _{i}) \sim {\text{Kategorisk}}\left({\frac {\pi _{j}}{\sum _{i}\pi _{i}}}\right)_{j}$ .
• $\max _{i}(g_{i}+\log \pi _{i })\sim {\text{Gumbel}}\left(-\gamma +\log \left(\sum _{i}\pi _{i}\right),1\right)$ . Det vill säga att Gumbel-distributionen är en max-stabil distributionsfamilj.
• $\mathbb {E} [\max _{i}(g_{i}+\beta x_{i })]=\log \left(\sum _{i}e^{\beta x_{i}}\right)$ .

Slumpmässig variationsgenerering

Ytterligare information: Ojämn generering av slumpmässiga variationer

Eftersom kvantilfunktionen (invers kumulativ fördelningsfunktion ), $Q(p)$ , av en Gumbelfördelning ges av

$Q(p)=\mu -\beta \ln(-\ln(p)),$

varianten $Q(U)$ har en Gumbel-fördelning med parametrarna $\mu$ och $\beta$ när slumpvarianten $U$ dras från uniformen fördelning på intervallet $(0,1)$ .

Sannolikhetspapper

En bit millimeterpapper som innehåller Gumbel-fördelningen.

I tider före programvaran användes sannolikhetspapper för att avbilda Gumbel-fördelningen (se illustration). Papperet är baserat på linjärisering av den kumulativa fördelningsfunktionen $F$ :

$-\ln[-\ln(F)]=(x-\mu )/\beta$

I papperet är den horisontella axeln konstruerad i en dubbel stockskala. Den vertikala axeln är linjär. Genom att plotta $F$ på papperets horisontella axel och $x$ -variabeln på den vertikala axeln, representeras fördelningen av en rät linje med en lutning 1 $/\beta$ . När distributionsanpassningsprogramvara som CumFreq blev tillgänglig gjordes uppgiften att plotta distributionen enklare, vilket visas i avsnittet nedan.

Se även

• Typ-2 Gumbel distribution
• Extremvärdesteori
• Generaliserad extremvärdesfördelning
• Fisher–Tippett–Gnedenkos sats
• Emil Julius Gumbel