Inlindad Cauchy distribution

Inlindad Cauchy

Sannolikhetstäthetsfunktion 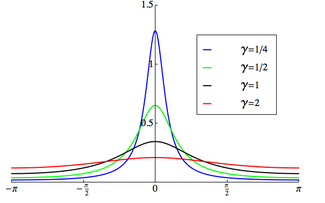Stödet är valt att vara [-π,π)
Kumulativ fördelningsfunktion Stödet är valt att vara [-π,π)
Parametrar	$\mu$ Real $\gamma >0$
Stöd	$-\pi \leq \theta <\pi$
PDF	${\frac {1}{2\pi }}\,{\frac {\sinh(\gamma )}{ \cosh(\gamma )-\cos(\theta -\mu )}}$
CDF	$\,$
Betyda	$\mu$ (cirkulär)
Variation	$1-e^{-\gamma }$ (cirkulär)
Entropi	$\ln(2\pi (1-e^{-2\gamma }))$ (differential)
CF	$e^{in\mu -|n|\gamma }$

Inom sannolikhetsteori och riktningsstatistik är en inlindad Cauchy-fördelning en inlindad sannolikhetsfördelning som är ett resultat av "lindningen" av Cauchy-fördelningen runt enhetscirkeln . Cauchy-fördelningen är ibland känd som en Lorentz-fördelning, och den inslagna Cauchy-fördelningen kan ibland kallas en inslagen Lorentzi-fördelning.

Den lindade Cauchy-fördelningen finns ofta inom spektroskopi där den används för att analysera diffraktionsmönster (se t.ex. Fabry–Pérot interferometer) .

Beskrivning

Sannolikhetstäthetsfunktionen för den lindade Cauchy-fördelningen är :

$f_{WC}( ;\mu ,\gamma )=\summa _{n=-\infty }^{\infty }{\frac {\gamma }{\pi (\gamma ^{2}+(\theta -\mu +2\ pi n)^{2})}}\qquad -\pi <\theta <\pi$

där $\gamma$ är skalfaktorn och $\mu$ är topppositionen för den "oupppackade" fördelningen. Att uttrycka ovanstående pdf i termer av den karakteristiska funktionen för Cauchy-fördelningen ger:

$f_{WC}(\theta ;\mu ,\gamma )={\frac {1}{2\pi }}\ summa _{n=-\infty }^{\infty }e^{in(\theta -\mu )-|n|\gamma }={\frac {1}{2\pi }}\,\,{ \frac {\sinh \gamma }{\cosh \gamma -\cos(\theta -\mu )}}$

PDF:en kan också uttryckas i termer av den cirkulära variabeln z = e ^iθ och den komplexa parametern ζ = e ^{i ( μ + iγ )}

$f_{WC}(z;\zeta )={\frac {1}{2\pi }}\,\,{\frac {1-|\zeta |^{2}}{|z- \zeta |^{2}}}$

där, som visas nedan, ζ = ⟨ z ⟩.

När det gäller den cirkulära variabeln $z=e^{i\theta }$ är de cirkulära momenten för den lindade Cauchy-fördelningen den karakteristiska funktionen för Cauchy-fördelningen utvärderad med heltalsargument:

$\langle z^{n}\rangle =\int _{\Gamma }e^{in\theta }\,f_{WC}(\theta ;\mu ,\gamma )\,d\theta =e ^{in\mu -|n|\gamma }.$

där $\Gamma \,$ är något intervall med längden $2\pi$ . Det första ögonblicket är då medelvärdet av z , även känt som medelresultant, eller medelresultatvektor:

$\langle z\rangle =e^{i\mu -\gamma }$

Medelvinkeln är

$\langle \theta \rangle =\mathrm {Arg} \langle z\rangle =\mu$

och längden på medelresultanten är

$R=|\langle z\rangle |=e^{-\gamma }$

ger en cirkulär varians på 1 − R .

Uppskattning av parametrar

En serie av N mätningar $z_{n}=e^{i\theta _{n}}$ dragna från en lindad Cauchy-fördelning kan användas för att uppskatta vissa parametrar för fördelningen. Genomsnittet av serien ${\overline {z}}$ definieras som

${\overline {z}}={\frac {1}{N}}\summa _{n=1}^{N}z_{n}$

och dess förväntningsvärde kommer bara att vara det första ögonblicket:

$\langle {\overline {z}}\rangle =e^{i\mu -\gamma }$

Med andra ord, ${\overline {z}}$ är en opartisk estimerare av det första ögonblicket. Om vi ​​antar att topppositionen $\mu$ ligger i intervallet $[-\pi ,\pi )$ , då Arg $({\overline {z}})$ kommer att vara en (biased) estimator av topppositionen $\mu$ .

Om man ser $z_{n}$ som en uppsättning vektorer i det komplexa planet, är ${\overline {R}}^{2}$ -statistiken längden på den genomsnittliga vektorn:

${\overline {R}}^ {2}={\overline {z}}\,{\overline {z^{*}}}=\left({\frac {1}{N}}\summa _{n=1}^{N} \cos \theta _{n}\right)^{2}+\left({\frac {1}{N}}\summa _{n=1}^{N}\sin \theta _{n}\ höger)^{2}$

och dess förväntningsvärde är

$\langle {\overline {R}}^{2}\rangle ={\frac {1}{N}}+{\frac {N-1}{N}}e^{-2\gamma } .$

Med andra ord statistiken

$R_{e}^{2}={\frac {N}{N-1}}\left({\overline {R}} ^{2}-{\frac {1}{N}}\right)$

kommer att vara en opartisk skattare av $e^{-2\gamma }$ , och $\ln(1/R_{e}^{2 })/2$ kommer att vara en (biased) estimator av $\gamma$ .

Entropi

Informationsentropin för den lindade Cauchy - fördelningen definieras som:

$H=-\int _{\Gamma }f_{WC}(\ theta ;\mu ,\gamma )\,\ln(f_{WC}(\theta ;\mu ,\gamma ))\,d\theta$

där $\Gamma$ är vilket intervall som helst med längden $2\pi$ . Logaritmen för densiteten för den lindade Cauchy-fördelningen kan skrivas som en Fourier-serie i $\theta \,$ :

$\ln(f_{WC}(\theta ;\mu,\gamma ))=c_{0}+2\summa _{m=1}^{\infty }c_{m}\cos(m\theta )$

var

$c_{m}={\frac {1}{2 \pi }}\int _{\Gamma }\ln \left({\frac {\sinh \gamma }{2\pi (\cosh \gamma -\cos \theta )}}\right)\cos(m\ theta )\,d\theta$

Vilket ger:

$c_{0}=\ln \left({\frac {1-e^{-2\gamma }}{2\pi }}\right )$

(jfr Gradshteyn och Ryzhik 4.224.15) och

$c_{m}={\frac {e^{-m\gamma }}{m}}\qquad \mathrm {for} \,m>0$

(jfr Gradshteyn och Ryzhik 4.397.6). Den karakteristiska funktionsrepresentationen för den lindade Cauchy-fördelningen på vänster sida av integralen är:

$f_{WC}(\theta ;\mu,\gamma )= {\frac {1}{2\pi }}\left(1+2\sum _{n=1}^{\infty }\phi _{n}\cos(n\theta)\right)$

där $\phi _{n}=e^{-|n|\gamma }$ . Genom att ersätta dessa uttryck i entropiintegralen, byta ut ordningen för integration och summering och använda ortogonaliteten hos cosinus, kan entropin skrivas:

$H=-c_{ 0}-2\sum _{m=1}^{\infty }\phi _{m}c_{m}=-\ln \left({\frac {1-e^{-2\gamma }}{ 2\pi }}\right)-2\sum _{m=1}^{\infty }{\frac {e^{-2n\gamma }}{n}}$

Serien är bara Taylor-expansionen för logaritmen av $(1-e^{-2\gamma })$ så entropin kan skrivas i sluten form som:

$H=\ln(2\pi (1-e^{-2\gamma }))\,$

Cirkulär Cauchy-fördelning

Om X är Cauchy fördelad med median μ och skalparameter γ, då den komplexa variabeln

$Z={\frac {Xi}{X+i}}$

har enhetsmodul och är fördelad på enhetscirkeln med densitet:

$f_{CC}(\theta ,\mu ,\gamma )={\frac {1}{2\pi }}{\frac {1-|\zeta |^{2}}{|e^ {i\theta }-\zeta |^{2}}}$

var

$\zeta ={\frac {\psi -i}{\psi +i}}$

och ψ uttrycker de två parametrarna för den associerade linjära Cauchy-fördelningen för x som ett komplext tal:

$\psi =\mu +i\gamma \,$

Det kan ses att den cirkulära Cauchy-fördelningen har samma funktionella form som den lindade Cauchy-fördelningen i z och ζ (dvs. f _WC (z,ζ)). Den cirkulära Cauchy-fördelningen är en omparametriserad inlindad Cauchy-fördelning:

$f_{CC}(\theta ,m,\gamma )=f_ {WC}\left(e^{i\theta},\,{\frac {m+i\gamma -i}{m+i\gamma +i}}\right)$

Fördelningen $f_{CC}(\theta ;\mu ,\gamma )$ kallas den cirkulära Cauchyfördelningen (även den komplexa Cauchyfördelningen) med parametrarna μ och γ. (Se även McCullaghs parametrisering av Cauchy-distributionerna och Poisson-kärnan för relaterade begrepp.)

Den cirkulära Cauchy-fördelningen uttryckt i komplex form har ändliga moment av alla ordningar

$\operatorname {E} [Z^{n}]=\zeta ^{n},\quad \operatorname {E } [{\bar {Z}}^{n}]={\bar {\zeta }}^{n}$

för heltal n ≥ 1. För |φ| < 1, förvandlingen

$U(z,\phi )={\frac {z-\phi }{1-{\bar {\phi }}z}}$

är holomorf på enhetsskivan, och den transformerade variabeln U ( Z , φ) är fördelad som komplex Cauchy med parametern U (ζ, φ).

Givet ett urval z ₁ , ..., z _n av storleken n > 2, maximal sannolikhetsekvationen

$n^{-1}U\left(z,{\hat {\zeta }}\right) =n^{-1}\summa U\left(z_{j},{\hat {\zeta }}\right)=0$

kan lösas med en enkel fixpunkts iteration:

$\zeta ^{(r+1)}=U\vänster(n^{- 1}U(z,\zeta ^{(r)}),\,-\zeta ^{(r)}\right)\,$

börjar med ζ ⁽⁰⁾ = 0. Sekvensen av sannolikhetsvärden är icke-minskande och lösningen är unik för prover som innehåller minst tre distinkta värden.

Maximal sannolikhetsuppskattning för medianen ( ${\hat {\mu }}$ ) och skalparametern ( ${\displaystyle {\hat {\gamma }}})$ för ett verkligt Cauchy-prov erhålls genom den omvända transformationen:

${\hat {\mu }}\pm i{\hat {\gamma }}=i{\frac {1+{\hat {\zeta }}}{1-{\hat {\zeta }} }}.$

För n ≤ 4 är uttryck i sluten form kända för ${\hat {\zeta }}$ . Tätheten för skattaren för maximal sannolikhet vid t i enhetsskivan är nödvändigtvis av formen:

${\frac {1}{4\pi }}{\frac {p_{n}(\chi ( t,\zeta ))}{(1-|t|^{2})^{2}}},$

var

$\chi (t,\zeta )={\frac {|t-\zeta |^{2}}{4(1- |t|^{2})(1-|\zeta |^{2})}}$ .

Formler för p ₃ och p ₄ finns tillgängliga.

Se även

• Inslagen distribution
• Dirac kam
• Inlindad normalfördelning
• Cirkulär enhetlig fördelning
• McCullaghs parametrisering av Cauchy-distributionerna

•   Borradaile, Graham (2003). Statistik över geovetenskapliga data . Springer . ISBN 978-3-540-43603-4 . Hämtad 31 dec 2009 .
•   Fisher, NI (1996). Statistisk analys av cirkulär data . Cambridge University Press . ISBN 978-0-521-56890-6 . Hämtad 2010-02-09 .