Beställningsstatistik

Sannolikhetstäthetsfunktioner för ordningsstatistiken för ett urval av storlek n = 5 från en exponentiell fördelning med enhetsskalaparameter

I statistik är k : te ordningens statistik för ett statistiskt urval lika med dess k: te minsta värde. Tillsammans med rankstatistik är ordningsstatistik bland de mest grundläggande verktygen i icke-parametrisk statistik och slutledning .

Viktiga specialfall av orderstatistiken är det lägsta och högsta värdet av ett prov, och (med vissa kvalifikationer som diskuteras nedan) provmedianen och andra provkvantiler .

När man använder sannolikhetsteori för att analysera orderstatistik för slumpmässiga urval från en kontinuerlig fördelning , används den kumulativa fördelningsfunktionen för att reducera analysen till fallet med orderstatistik för den enhetliga fördelningen .

Notation och exempel

Anta till exempel att fyra siffror observeras eller registreras, vilket resulterar i ett urval av storlek 4. Om urvalsvärdena är

6, 9, 3, 8,

orderstatistiken skulle betecknas

$x_{(1)}=3,\ \ x_{(2)}=6 ,\ \ x_{(3)}=8,\ \ x_{(4)}=9,\,$

där nedsänkningen ( i ) inom parentes indikerar den i:te ordningens statistik för provet.

Första ordningens statistik (eller minsta ordningens statistik ) är alltid minimum av urvalet, det vill säga

$X_{(1)}=\min\{\,X_{1},\ldots ,X_{n}\,\}$

där vi, enligt en vanlig konvention, använder versaler för att referera till slumpvariabler, och gemener (enligt ovan) för att referera till deras faktiska observerade värden.

På liknande sätt, för ett urval av storlek n , är n :te ordningens statistik (eller största ordningens statistik ) det maximala , dvs.

$X_{(n)}=\max\{\,X_{1},\ldots ,X_{n}\,\}.$

Sampelintervallet är skillnaden mellan maximum och minimum . Det är en funktion av orderstatistiken:

${\rm {Range}}\{\,X_{1},\ldots ,X_{n}\,\}=X_{(n)}-X_{(1)}.$

En liknande viktig statistik inom explorativ dataanalys som helt enkelt är relaterad till orderstatistiken är det interkvartila urvalet .

Urvalsmedianen kan vara en ordningsstatistik eller inte, eftersom det bara finns ett enda mittvärde när antalet n observationer är udda . Närmare bestämt, om n = 2 m +1 för något heltal m , så är sampelmedianen $X_{(m+1)}$ och så är en ordningsstatistik. Å andra sidan, när n är jämn , n = 2 m och det finns två mittvärden, $X_{(m)}$ och $X_{(m+ 1)}$ , och urvalsmedianen är någon funktion av de två (vanligtvis genomsnittet) och därför inte en ordningsstatistik. Liknande anmärkningar gäller för alla provkvantiler.

Probabilistisk analys

Givet eventuella slumpvariabler X ₁ , X ₂ ..., X _n , är ordningsstatistiken X ₍₁₎ , X ₍₂₎ , ..., X _{( n )} också slumpvariabler, definierade genom att sortera värdena ( realisationer ) av X1 _, ..., _Xn i stigande ordning.

När de slumpmässiga variablerna X ₁ , X ₂ ..., Xn bildar ett urval är de oberoende och identiskt _fördelade . Detta är fallet som behandlas nedan. Generellt sett kan de slumpmässiga variablerna X ₁ , ..., X _n uppstå genom sampling från mer än en population. Sedan är de oberoende , men inte nödvändigtvis identiskt fördelade, och deras gemensamma sannolikhetsfördelning ges av Bapat–Beg-satsen .

Från och med nu kommer vi att anta att de slumpvariabler som övervägs är kontinuerliga och, där det är lämpligt, kommer vi också att anta att de har en sannolikhetstäthetsfunktion (PDF), det vill säga att de är absolut kontinuerliga . Särdragen med analysen av fördelningar som tilldelar massa till poäng (särskilt diskreta fördelningar ) diskuteras i slutet.

Kumulativ fördelningsfunktion för orderstatistik

För ett slumpmässigt urval enligt ovan, med kumulativ fördelning $F_{X}(x)$ , har orderstatistiken för det urvalet kumulativa fördelningar enligt följande (där r anger vilken orderstatistik):

$F_{X_{(r)}} (x)=\summa _{j=r}^{n}{\binom {n}{j}}[F_{X}(x)]^{j}[1-F_{X}(x)] ^{nj}$

motsvarande sannolikhetstäthetsfunktion kan härledas från detta resultat och befinns vara det

$f_{X_{(r)}}(x)={\frac {n!}{(r-1)!(nr)!}}f_{X}(x)[F_{X}(x) )]^{r-1}[1-F_{X}(x)]^{nr}.$

Dessutom finns det två specialfall, som har CDF:er som är lätta att beräkna.

$F_{X_{(n)}}(x)= \operatörsnamn {Prob} (\max\{\,X_{1},\ldots ,X_{n}\,\}\leq x)=[F_{X}(x)]^{n}$

$F_{X_{(1)}}(x) =\operatörsnamn {Prob} (\min\{\,X_{1},\ldots ,X_{n}\,\}\leq x)=1-[1-F_{X}(x)]^{n }$

Vilket kan härledas genom noggrant övervägande av sannolikheter.

Sannolikhetsfördelningar av orderstatistik

Orderstatistik samplad från en enhetlig fördelning

I detta avsnitt visar vi att ordningsstatistiken för den enhetliga fördelningen på enhetsintervallet har marginalfördelningar som tillhör betafördelningsfamiljen . Vi ger också en enkel metod för att härleda den gemensamma distributionen av valfritt antal orderstatistik, och slutligen översätter dessa resultat till godtyckliga kontinuerliga distributioner med hjälp av cdf .

Vi antar genom hela detta avsnitt att $X_{1},X_{2},\ldots ,X_{n}$ är ett slumpmässigt urval från en kontinuerlig fördelning med cdf $F_{X}$ . Betecknar $U_{i}=F_{X}(X_{i})}$$U_{1}, \ldots ,U_{n}$ får vi motsvarande slumpmässiga urval från den enhetliga standardfördelningen . Observera att orderstatistiken även uppfyller $U_{(i)}=F_{X}(X_{(i)})$ .

Sannolikhetstäthetsfunktionen för orderstatistiken $U_{(k)}$ är lika med

$f_{U_{(k)}}(u)={n! \över (k-1)!(nk)!}u^{k-1}(1-u)^{nk}$

det vill säga att k: te ordningens statistik för den enhetliga fördelningen är en beta-fördelad slumpvariabel.

$U_{(k)}\sim \operatörsnamn {Beta} (k,n+1\mathbf {-} k).$

Beviset för dessa uttalanden är följande. För att $U_{(k)}$ ska vara mellan u och u + du , är det nödvändigt att exakt k − 1 element i urvalet är mindre än u , och att minst ett är mellan u och u + d u . Sannolikheten att mer än en finns i det senare intervallet är redan $O(du^{2})$ , så vi måste beräkna sannolikheten för att exakt k − 1, 1 och n − k observationer faller i intervallen $(0,u)$ , $(u,u+du)$ och $(u+du,1)$ respektive. Detta är lika med (se multinomial distribution för detaljer)

${n! \över (k-1)!(nk)!}u^{k-1}\cdot du\cdot (1-u-du)^{nk}$

och resultatet följer.

Medelvärdet för denna fördelning är k / ( n + 1).

Den gemensamma fördelningen av den enhetliga fördelningens orderstatistik

På liknande sätt, för i < j , kan den gemensamma sannolikhetstäthetsfunktionen för tvåordningsstatistiken U _{( i )} < U _{( j )} visas vara

$f_{U_{(i)},U_{(j)}}(u,v)=n!{u^{i-1} \over (i-1)!}{(vu)^{ ji-1} \over (ji-1)!}{(1-v)^{nj} \over (nj)!}$

vilket är (upp till termer av högre ordning än $O(du\,dv)$ ) sannolikheten att i − 1, 1, j − 1 − i , 1 och n − j sampel element faller i intervallen $(0,u)$ , $(u,u+du)$ , $(u+du,v)$ , $(v,v+dv)$ , $(v+dv,1)$ respektive.

Man resonerar på ett helt analogt sätt för att härleda de högre ordningens gemensamma fördelningar. Kanske överraskande visar sig den gemensamma tätheten för n -ordningens statistik vara konstant :

$f_{U_{(1)},U_{(2)},\ldots ,U_{(n)}}(u_{1},u_{2},\ldots ,u_{n})=n !.$

Ett sätt att förstå detta är att det oordnade provet har konstant densitet lika med 1, och att det finns n ! olika permutationer av provet som motsvarar samma sekvens av orderstatistik. Detta hänger samman med att 1/ n ! är volymen för regionen $0<u_{1}<\cdots <u_{n}<1$ . Det är också relaterat till en annan särdrag av ordningsstatistik för enhetliga slumpvariabler: Det följer av BRS -olikheten att det maximala förväntade antalet enhetliga U(0,1] slumpvariabler man kan välja från ett urval av storlek n med en summa upp inte överstiger $0<s<n/2$ begränsas ovan av ${\displaystyle {\sqrt {2sn}}} ,$ som alltså är invariant på mängden av alla $s,n$ med konstant produkt $sn$ .

Med hjälp av formlerna ovan kan man härleda fördelningen av intervallet för orderstatistiken, det vill säga fördelningen av $U_{(n)}-U_{(1)}$ , dvs max minus minimum. Mer allmänt, för $n\geq k>j\geq 1$ , $U_{(k)}-U_{(j)}$ har också en betadistribution:

$$U_{(k)}-U_{(j)}\sim \operatörsnamn {Beta} (kj,n-(kj)+1)$$

Från dessa formler kan vi härleda kovariansen mellan två ordningsstatistik:

$$\operatorname {Cov} (U_{(k)},U_ {(j)})={\frac {j(n-k+1)}{(n+1)^{2}(n+2)}}$$

Formeln följer av att notera det

$$\operatörsnamn {Var} (U_{(k)}-U_{(j)})=\operatörsnamn {Var} (U_{(k)})+\operatörsnamn {Var} (U_{( j)})-2\cdot \operatörsnamn {Cov} (U_{(k)},U_{(j)})={\frac {k(n-k+1)}{(n+1)^{ 2}(n+2)}}+{\frac {j(n-j+1)}{(n+1)^{2}(n+2)}}-2\cdot \operatörsnamn {Cov} ( U_{(k)},U_{(j)})$$

och jämföra det med

$$\operatorname {Var} (U)={\frac {( kj)(n-(kj)+1)}{(n+1)^{2}(n+2)}}$$

där ${\displaystyle U\sim \operatörsnamn {Beta} (kj,n-(kj)+1)} ,$ vilket är den faktiska fördelningen av skillnaden.

Orderstatistik samplad från en exponentiell fördelning

För $X_{1},X_{2},..,X_{n}$ ett slumpmässigt urval av storlek n från en exponentialfördelning med parametern λ , orderstatistiken X _{( i )} för i = 1, 2,3, ..., n var och en har fördelning

$X_{(i)}{\stackrel {d}{=}}{\frac {1}{\lambda }}\left(\sum _{j=1}^{i}{\frac {Z_{j}}{n-j+1}}\right)$

där Zj är iid standardexponentiella slumpvariabler (dvs med hastighetsparameter 1) _. Detta resultat publicerades först av Alfréd Rényi .

Orderstatistik samplad från en Erlang-distribution

Laplace -transformeringen av orderstatistik kan samplas från en Erlang-distribution via en vägräkningsmetod [ .

Den gemensamma fördelningen av orderstatistiken av en absolut kontinuerlig fördelning

Om F _X är absolut kontinuerlig , har den en densitet så att $dF_{X}(x)=f_{X}(x)\,dx$ , och vi kan använda ersättningarna

$u=F_{X}(x)$

och

$du=f_{X}(x)\,dx$

för att härleda följande sannolikhetstäthetsfunktioner för ordningsstatistiken för ett urval av storlek n från fördelningen av X :

$f_{X_{(k)}}(x)={\frac {n!} {(k-1)!(nk)!}}[F_{X}(x)]^{k-1}[1-F_{X}(x)]^{nk}f_{X}(x)$

$f_{X_{(j)},X_{(k)}}(x,y)={\frac {n!}{(j-1)!(kj-1)!(nk)!} [F_{X}(x)]^{j-1}[F_{X}(y)-F_{X}(x)]^{k-1-j}[1-F_{X}(y )]^{nk}f_{X}(x)f_{X}(y)$ där $x\leq y$

$f_{X_{(1)},\ldots ,X_{(n)}}(x_{1},\ldots ,x_{n})= n!f_{X}(x_{1})\cdots f_{X}(x_{n})$ där $x_{1}\leq x_{2}\leq \dots \leq x_{n}.$

Användning: konfidensintervall för kvantiler

En intressant fråga är hur väl orderstatistiken presterar som estimerare av kvantilerna i den underliggande fördelningen.

Ett exempel i liten provstorlek

Det enklaste fallet att överväga är hur väl urvalsmedianen uppskattar populationsmedianen.

Som ett exempel, betrakta ett slumpmässigt urval av storlek 6. I så fall definieras urvalsmedianen vanligtvis som mittpunkten av intervallet avgränsat av 3:e och 4:e ordningens statistik. Men vi vet från den föregående diskussionen att sannolikheten att detta intervall faktiskt innehåller populationsmedianen är [

${6 \choose 3}(1/2)^{6}={5 \over 16}\approx 31\%.$

Även om urvalsmedianen förmodligen är bland de bästa fördelningsoberoende punktuppskattningarna av populationsmedianen, är vad detta exempel illustrerar att det inte är särskilt bra i absoluta tal. I detta speciella fall är ett bättre konfidensintervall för medianen det som avgränsas av 2:a och 5:e ordningens statistik, som innehåller populationsmedianen med sannolikhet

$\left[{6 \choose 2}+{6 \choose 3}+{6 \choose 4}\right](1/2)^{6}={25 \over 32}\approx 78\% .$

Med en så liten urvalsstorlek, om man vill ha minst 95% konfidens, reduceras man till att säga att medianen ligger mellan minimum och maximum av de 6 observationerna med sannolikhet 31/32 eller ungefär 97%. Storlek 6 är i själva verket den minsta urvalsstorleken så att intervallet som bestäms av minimum och maximum är minst ett 95 % konfidensintervall för populationsmedianen.

Stora provstorlekar

För den likformiga fördelningen, eftersom n tenderar till oändligheten, är den p ^:te provkvantilen asymptotiskt normalfördelad eftersom den approximeras av

$U_{(\lceil np\rceil )}\sim AN\left(p,{\frac {p(1-p)}{n}}\right).$

För en allmän fördelning F med en kontinuerlig densitet som inte är noll vid F ⁻¹ ( p ), gäller en liknande asymptotisk normalitet:

$X_{(\lceil np\rceil ) }\sim AN\left(F^{-1}(p),{\frac {p(1-p)}{n[f(F^{-1}(p))]^{2}}} \höger)$

där f är densitetsfunktionen och F ⁻¹ är den kvantilfunktion som är associerad med F. En av de första personerna som nämnde och bevisade detta resultat var Frederick Mosteller i hans framstående artikel 1946. Ytterligare forskning ledde på 1960-talet till Bahadur -representationen som ger information om felgränserna.

En intressant observation kan göras i fallet där fördelningen är symmetrisk och populationsmedianen är lika med populationsmedelvärdet. I det här fallet är stickprovets medelvärde , med centrala gränssatsen , också asymptotiskt normalfördelad, men med varians σ ² /n istället. Denna asymptotiska analys tyder på att medelvärdet överträffar medianen i fall av låg kurtos och vice versa. Till exempel uppnår medianen bättre konfidensintervall för Laplace-fördelningen , medan medelvärdet presterar bättre för X som är normalfördelade.

Bevis

Det kan man visa

$B(k,n+1-k)\ {\stackrel {\mathrm {d} }{=}}\ {\frac { X}{X+Y}},$

var

$X=\sum _{i=1}^{k}Z_{i},\quad Y= \sum _{i=k+1}^{n+1}Z_{i},$

där Z _i är oberoende identiskt fördelade exponentiella slumpvariabler med hastighet 1. Eftersom X / n och Y / n är asymptotiskt normalfördelade av CLT, följer våra resultat genom tillämpning av deltametoden .

Användning: Icke-parametrisk densitetsuppskattning

Moment av fördelningen för första ordningens statistik kan användas för att utveckla en icke-parametrisk densitetsuppskattare. Antag att vi vill uppskatta densiteten $f_{X}$ vid punkten $x^{*}$ . Betrakta de slumpmässiga variablerna $Y_{i}=|X_{i}-x^{*}|$ , som är iid med fördelningsfunktionen $g_{Y}(y)=f_{X}(y+x^{*})+f_{X}(x^{*}-y)$ . Speciellt $f_{X}(x^{*})={\frac {g_{Y}(0)}{2}}$ .

Det förväntade värdet för första ordningens statistik $Y_{(1)}$ givet ett urval av $N$ totala observationsavkastningar,

$E( Y_{(1)})={\frac {1}{(N+1)g(0)}}+{\frac {1}{(N+1)(N+2)}}\int _{ 0}^{1}Q''(z)\delta _{N+1}(z)\,dz$

där $Q$ är kvantilfunktionen associerad med fördelningen $g_{Y}$ , och $\delta _ {N}(z)=(N+1)(1-z)^{N}$ . Denna ekvation i kombination med en jackknifing -teknik blir grunden för följande densitetsuppskattningsalgoritm,

 Indata: Ett urval av $N$ observationer. $\{x_{\ell }\}_{\ell =1}^{M}$ punkter för densitetsutvärdering. Stämningsparameter  $a\in (0,1)$ (vanligtvis 1/3). Utdata:  ${\displaystyle \{{\hat {f}}_{\ell }\}_{\ell =1}^{M}} uppskattad densitet$ vid utvärderingspunkterna. 

      1: Set ${\displaystyle m_{N}=\operatörsnamn {round} (N^{1-a})} 2:$ Set $s_ {N}={\frac {N}{m_{N}}}$ 3: Skapa en $s_{N}\times m_{N}$ matris $M_{ ij}$ som innehåller $m_{N}$ delmängder med $s_{N}$ observationer vardera. 4: Skapa en vektor  ${\hat {f}}$ för att hålla densitetsutvärderingarna. 5:   för $\ell =1\to M$ till  6:  för $k=1\to m_{N}$ till  7: Hitta närmaste avstånd $d_{\ell k}$ till den aktuella punkten $x_{\ell }$ inom $​​{\displaystyle k}:$ e delmängden 8:  slut för  9: Beräkna delmängdens medelvärde av avstånd till $x_{\ell }:d_{\ell }=\summa _{k=1}^{m_{N}}{\frac {d_{\ell k}}{m_{N}}}$ 10: Beräkna densitetsuppskattningen vid ${\displaystyle x_{\ell }:{ \hat {f}}_{\ell }={\frac {1}{2(1+s_{N})d_{\ell }}}} 11: slut för 12: returnera$ f  ^  {  \ $\ hatt {f}}}$

I motsats till de bandbredds/längdbaserade avstämningsparametrarna för histogram- och kärnbaserade tillvägagångssätt, är avstämningsparametern för den ordningsstatistiska baserade densitetsuppskattaren storleken på provdelmängder. En sådan estimator är mer robust än histogram- och kärnbaserade tillvägagångssätt, till exempel kan densiteter som Cauchy-fördelningen (som saknar ändliga moment) härledas utan behov av specialiserade modifieringar såsom IQR- baserade bandbredder . Detta beror på att det första momentet i orderstatistiken alltid existerar om det förväntade värdet av den underliggande fördelningen gör det, men det omvända är inte nödvändigtvis sant.

Att hantera diskreta variabler

Antag att $X_{1},X_{2},\ldots ,X_{n}$ är iid slumpvariabler från en diskret fördelning med kumulativ fördelningsfunktion ${\ displaystyle F(x)}$ och sannolikhetsmassfunktion $f(x)$ . För att hitta sannolikheterna för $k^{\text{th}}$ ordningsstatistiken behövs först tre värden, nämligen

$p_{1}=P(X<x)=F(x)-f(x),\ p_{2}=P(X=x)=f(x),{\text{ och }} p_{3}=P(X>x)=1-F(x).$

Den kumulativa fördelningsfunktionen för $k^{\text{th}}$ ordningsstatistiken kan beräknas genom att notera att

${\begin{aligned}P(X_{(k)}\leq x)&=P({\text{det finns minst }}k{\text{ observationer mindre än eller lika med }}x) ,\\&=P({\text{det finns som mest }}nk{\text{ observationer större än }}x),\\&=\summa _{j=0}^{nk}{n \choose j}p_{3}^{j}(p_{1}+p_{2})^{nj}.\end{aligned}}$

På liknande sätt ges ${\displaystyle P(X_{(k)}<x)} av$

${\begin{aligned}P(X_{(k)}<x)&=P({\text{det finns minst }}k{\text{ observationer mindre än }}x),\\& =P({\text{det finns som mest }}nk{\text{ observationer större än eller lika med }}x),\\&=\summa _{j=0}^{nk}{n \choose j }(p_{2}+p_{3})^{j}(p_{1})^{nj}.\end{aligned}}$

Observera att sannolikhetsmassfunktionen för $X_{(k)}$ bara är skillnaden mellan dessa värden, det vill säga

${\begin{aligned}P(X_{(k)}=x)&=P(X_{(k)}\leq x)-P(X_{(k)}<x),\\& =\summa _{j=0}^{nk}{n \choose j}\left(p_{3}^{j}(p_{1}+p_{2})^{nj}-(p_{2} }+p_{3})^{j}(p_{1})^{nj}\höger),\\&=\summa _{j=0}^{nk}{n \choose j}\left( (1-F(x))^{j}(F(x))^{nj}-(1-F(x)+f(x))^{j}(F(x)-f(x) )^{nj}\right).\end{aligned}}$

Beräkningsorderstatistik

Huvudartiklar: Urvalsalgoritm och Sampling i ordning

Problemet med att beräkna det k: te minsta (eller största) elementet i en lista kallas urvalsproblemet och löses med en urvalsalgoritm. Även om detta problem är svårt för mycket stora listor, har sofistikerade urvalsalgoritmer skapats som kan lösa detta problem i tid proportionellt mot antalet element i listan, även om listan är helt oordnad. Om data lagras i vissa specialiserade datastrukturer kan denna tid föras ner till O(log n ). I många applikationer krävs all orderstatistik, i vilket fall en sorteringsalgoritm kan användas och tiden det tar är O( n log n ).

Se även

• Rankit
• Box tomt
• BRS-ojämlikhet
• Samtidigt (statistik)
• Fisher–Tippett distribution
• Bapat–Beg-satsen för ordningsstatistiken för oberoende men inte nödvändigtvis identiskt fördelade slumpvariabler
• Bernstein polynom
• L-estimator – linjära kombinationer av orderstatistik
• Rang-storleksfördelning
• Urvalsalgoritm

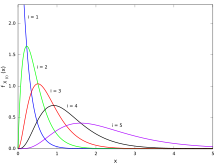
Exempel på orderstatistik

• Prov max och minimum
• Kvantil
• Percentil
• Decil
• Kvartil
• Median

externa länkar

• Beställningsstatistik hos PlanetMath . Hämtad 2005-02-02
• Weisstein, Eric W. "Orderstatistik" . MathWorld . Hämtad 2005-02-02
• C++-källa Dynamisk orderstatistik