Gini koefficient

Världskarta över inkomstojämlikhet Gini-koefficienter per land (som %). Baserat på Världsbankens data från 1992 till 2020.

Över 50
Mellan 45 och 50
Mellan 40 och 45
Mellan 35 och 40
Mellan 30 och 35
Under 30
Inga data

En karta som visar Gini-koefficienter för välstånd inom länder för 2019

Global andel av förmögenhet per förmögenhetsgrupp. Omritad från data från Credit Suisse, 2021

Inom ekonomi är Gini -koefficienten ( / på statistisk ) ˈdʒiːn i / JEE -nee , även känd som Gini-index eller Gini-kvot , ett mått spridning avsett att representera inkomstojämlikheten eller ojämlikheten i förmögenhet inom en nation eller en social grupp . Den utvecklades av statistikern och sociologen Corrado Gini .

Gini-koefficienten mäter ojämlikheten mellan värden för en frekvensfördelning , såsom inkomstnivåer . En Gini-koefficient på 0 reflekterar perfekt jämlikhet , där alla inkomst- eller förmögenhetsvärden är desamma, medan en Gini-koefficient på 1 (eller 100%) reflekterar maximal ojämlikhet mellan värden. Till exempel, om alla har samma inkomst, blir Gini-koefficienten 0. Däremot indikerar en Gini-koefficient på 1 att inom en grupp människor har en enskild individ all inkomst eller konsumtion, medan alla andra inte har någon.

Gini-koefficienten föreslogs av Corrado Gini som ett mått på ojämlikhet i inkomst eller förmögenhet . För OECD-länder varierade inkomst Gini-koefficienten i slutet av 1900-talet, med tanke på effekten av skatter och transfereringar , mellan 0,24 och 0,49, med Slovenien som lägst och Mexiko högst. Afrikanska länder hade de högsta Gini-koefficienterna före skatt 2008–2009, med Sydafrika som hade världens högsta, uppskattad till 0,63 till 0,7, även om denna siffra sjunker till 0,52 efter att socialbidrag har beaktats, och sjunker igen till 0,47 efter beskattning. Den globala inkomstens Gini-koefficient 2005 har uppskattats till mellan 0,61 och 0,68 av olika källor.

Det finns några problem med att tolka en Gini-koefficient; samma värde kan vara resultatet av många olika fördelningskurvor. Den demografiska strukturen bör beaktas. Länder med en åldrande befolkning eller med ett ökat födelsetal upplever en ökande Gini-koefficient före skatt även om realinkomstfördelningen för arbetande vuxna förblir konstant. Forskare har utarbetat över ett dussin varianter av Gini-koefficienten.

Historia

Gini-koefficienten utvecklades av den italienske statistikern Corrado Gini och publicerades i hans 1912 uppsats Variability and Mutability ( italienska : Variabilità e mutabilità) . Med utgångspunkt i den amerikanske ekonomen Max Lorenz' arbete föreslog Gini att skillnaden mellan den hypotetiska räta linjen som visar perfekt jämlikhet och den faktiska linjen som visar människors inkomster, skulle användas som ett mått på ojämlikhet.

Definition

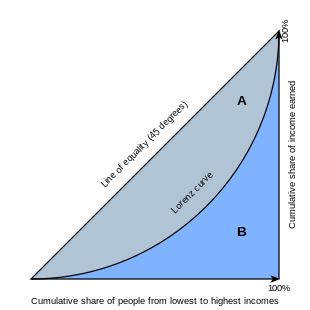
Grafisk representation av Gini-koefficienten:

Grafen visar att Gini-koefficienten är lika med arean markerad A dividerat med summan av areorna markerade A och B , det vill säga Gini = A /( A + B ) . Det är också lika med 2 A och med 1 − 2 B på grund av att A + B = 0,5 (eftersom axlarna skalar från 0 till 1).

Gini-koefficienten är ett index för graden av ojämlikhet i fördelningen av inkomst/förmögenhet, som används för att uppskatta hur långt ett lands förmögenhet eller inkomstfördelning avviker från en jämn fördelning.

Gini-koefficienten definieras vanligtvis matematiskt baserat på Lorenz-kurvan , som plottar andelen av befolkningens totala inkomst (y-axeln) som kumulativt tjänas av befolkningens nedersta x (se diagram). Linjen vid 45 grader representerar alltså perfekt jämställdhet i inkomster. Gini-koefficienten kan då ses som förhållandet mellan arean som ligger mellan jämlikhetslinjen och Lorenzkurvan (markerad A i diagrammet) över den totala arean under likhetslinjen (markerade A och B i diagrammet) ; dvs G = A /( A + B ) . Om det inte finns några negativa inkomster är det också lika med 2 A och med 1 − 2 B på grund av att A + B = 0,5 .

Anta att alla människor har icke-negativ inkomst (eller förmögenhet, beroende på vad som är fallet). I så fall kan Gini-koefficienten teoretiskt sträcka sig från 0 (fullständig jämställdhet) till 1 (fullständig ojämlikhet) och uttrycks ibland som en procentandel som sträcker sig mellan 0 och 100. Om negativa värden är möjliga (som rikedomen hos personer med skulder) , då skulle Gini-koefficienten teoretiskt kunna vara mer än 1. Vanligtvis antas medelvärdet (eller totalen) vara positivt, vilket utesluter en Gini-koefficient som är mindre än noll.

Ett alternativt tillvägagångssätt är att definiera Gini-koefficienten som hälften av den relativa genomsnittliga absoluta skillnaden, vilket är matematiskt ekvivalent med definitionen baserad på Lorenz-kurvan. Den genomsnittliga absoluta skillnaden är den genomsnittliga absoluta skillnaden för alla par av objekt i populationen, och den relativa genomsnittliga absoluta skillnaden är den genomsnittliga absoluta skillnaden dividerat med medelvärdet , ${\displaystyle {\bar {x}}} ,$ för att normalisera för skala. Om x _i är förmögenheten eller inkomsten för person i och det finns n personer, så ges Gini-koefficienten G av:

G={\frac {\displaystyle {\sum _{i=1}^{n}\summa _{j=1}^{n}\left|x_{i}-x_ {j}\right|}}{\displaystyle {2\sum _{i=1}^{n}\summa _{j=1}^{n}x_{j}}}}={\frac {\ displaystyle {\sum _{i=1}^{n}\sum _{j=1}^{n}\left|x_{i}-x_{j}\right|}}{\displaystyle {2n\sum _{j=1}^{n}x_{j}}}}={\frac {\displaystyle {\sum _{i=1}^{n}\summa _{j=1}^{n}\ vänster|x_{i}-x_{j}\right|}}{\displaystyle {2n^{2}{\bar {x}}}}}

När inkomstfördelningen (eller förmögenhetsfördelningen ges som en kontinuerlig sannolikhetstäthetsfunktion p ( x ), är Gini-koefficienten återigen hälften av den relativa genomsnittliga absoluta skillnaden:

G={\frac {1}{2\mu }}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }p(x )p(y)\,|xy|\,dx\,dy

där $\textstyle \mu =\int _{-\infty }^{\infty }xp(x)\,dx$ är medelvärdet av fördelningen, och de nedre gränserna för integration kan ersättas med noll när alla inkomster är positiva.

Beräkning

Rikaste u av befolkningen (röd) delar lika f av all inkomst eller förmögenhet; andra (gröna) delar lika på resten: G = f − u . En jämn fördelning (blå) med samma u och f har alltid G > f − u .

Även om inkomstfördelningen för ett visst land inte kommer att motsvara de teoretiska modellerna perfekt, kan dessa modeller ge en kvalitativ förklaring av inkomstfördelningen i en nation givet Gini-koefficienten.

Exempel: två inkomstnivåer

De extrema fallen representeras av det "mest jämställda" samhället där varje person får samma inkomst ( G = 0 ) och det "mest ojämlika" samhället (som består av N individer) där en ensam person får 100 % av den totala inkomsten och de återstående N − 1 personerna får inga ( G = 1 − 1/ N ).

Ett förenklat fall skiljer bara två inkomstnivåer, låg och hög. Om höginkomstgruppen är en andel u av befolkningen och tjänar en andel f av all inkomst, så är Gini-koefficienten f − u . En mer graderad fördelning med samma värden u och f kommer alltid att ha en högre Gini-koefficient än f − u .

Ett exempel på fall där de rikaste 20 % av befolkningen har 80 % av all inkomst (se Pareto-principen ) skulle leda till en Gini-inkomstkoefficient på minst 60 %.

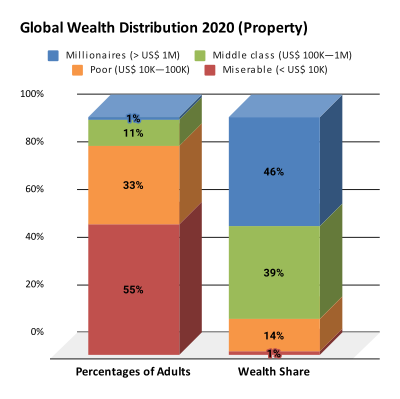
Ett annat exempelfall, där 1 % av världens befolkning äger 50 % av all förmögenhet, skulle resultera i en Gini-koefficient för förmögenhet på minst 49 %.

Alternativa uttryck

I vissa fall kan denna ekvation användas för att beräkna Gini-koefficienten utan direkt hänvisning till Lorenz-kurvan . Till exempel (med y för att ange inkomst eller förmögenhet för en person eller hushåll):

För en populationsuniform på värdena y _i , i = 1 till n , indexerad i icke-minskande ordning ( y _i ≤ y _{i +1} ):

{\displaystyle G={\frac {1}{n}}\left(n+1-2\left({\frac {\sum _{i=1}^{n}(n+1-i)y_ {i}}{\summa _{i=1}^{n}y_{i}}}\right)\right).} Detta kan förenklas till

:

G={\frac {2\sum _{i=1}^{n}iy_{i}}{n\sum _{i=1}^{n}y_{i}}}-{\ frac {n+1}{n}}.

Den här formeln gäller faktiskt för alla verkliga populationer, eftersom varje person kan tilldelas sin egen y _i .

Eftersom Gini-koefficienten är hälften av den relativa genomsnittliga absoluta skillnaden, kan den också beräknas med formler för den relativa genomsnittliga absoluta skillnaden. För ett slumpmässigt urval S som består av värden y _i , i = 1 till n , som är indexerade i icke-fallande ordning ( y _i ≤ y _{i +1} ), statistiken:

G(S)={\frac {1}{n-1}}\left(n+1-2\left({\frac {\sum _{i=1}^{n}(n+1-i)y_{i}}{\ summa _{i=1}^{n}y_{i}}}\right)\right)

är en konsekvent skattare av Gini-populationskoefficienten, men är i allmänhet inte opartisk . Liksom G har G : ( S ) en enklare form

G(S)=1-{\frac {2}{n-1}}\left(n-{\frac {\sum _{i=1}^{n}iy_{i}}{\ summa _{i=1}^{n}y_{i}}}\höger).

Det finns ingen provstatistik som i allmänhet är en opartisk skattare av Gini-populationskoefficienten, som den relativa genomsnittliga absoluta skillnaden .

Diskret sannolikhetsfördelning

För en diskret sannolikhetsfördelning med sannolikhetsmassfunktion $f(y_{i}),$ $i=1,\ldots ,n$ , där $f(y_{i})$ är andelen av befolkningen med inkomst eller förmögenhet $y_{i}>0$ , Gini-koefficienten är:

G={\frac {1}{2\mu }}\sum \limits _{i=1}^{n}\summa \limits _{j=1}^{n}\,f(y_ {i})f(y_{j})|y_{i}-y_{j}|

var

\mu =\sum \limits _{i=1}^{n}y_{i}f(y_{i}).

Om punkterna med sannolikheter som inte är noll indexeras i ökande ordning ${\displaystyle (y_{i}<y_{i+1})},$ då:

\frac {\sum _{i=1}^{n}f( y_{i})(S_{i-1}+S_{i})}{S_{n}}}}

var

S_{i}=\summa _{j=1}^{i}f(y_{j})\,y_{j}\,

och

S_{0}=0.

Dessa formler är också tillämpliga i gränsen, eftersom

n\rightarrow \infty .

Kontinuerlig sannolikhetsfördelning

När befolkningen är stor kan inkomstfördelningen representeras av en kontinuerlig sannolikhetstäthetsfunktion f ( x ) där f ( x ) dx är andelen av befolkningen med förmögenhet eller inkomst i intervallet dx omkring x . Om F ( x ) är den kumulativa fördelningsfunktionen för f ( x ):

F(x)=\int _{0}^{x}f(x)\,dx

och L ( x ) är Lorenz-funktionen:

L(x)={\frac {\int _{0}^{x}x\,f( x)\,dx}{\int _{0}^{\infty }x\,f(x)\,dx}}

då kan Lorenzkurvan L ( F ) representeras som en funktionsparametrisk i L ( x ) och F ( x ) och värdet på B kan hittas genom integration :

B=\int _{0}^{1}L(F)\,dF.

Gini-koefficienten kan också beräknas direkt från den kumulativa fördelningsfunktionen för fördelningen F ( y ). Genom att definiera μ som medelvärdet av fördelningen och specificera att F ( y ) är noll för alla negativa värden, ges Gini-koefficienten av:

G=1-{\frac {1 }{\mu }}\int _{0}^{\infty }(1-F(y))^{2}\,dy={\frac {1}{\mu }}\int _{0} ^{\infty }F(y)(1-F(y))\,dy

Det senare resultatet kommer från integrering av delar . (Observera att denna formel kan användas när det finns negativa värden om integrationen tas från minus oändlighet till plus oändlighet.)

Gini-koefficienten kan uttryckas i termer av kvantilfunktionen Q ( F ) (invers av den kumulativa fördelningsfunktionen: Q ( F ( x )) = x )

G={\frac {1}{2\mu }}\int _{0}^{1}\int _{0}^{1}|Q(F_{1})-Q(F_{ 2})|\,dF_{1}\,dF_{2}.

Eftersom Gini-koefficienten är oberoende av skalan , om fördelningsfunktionen kan uttryckas i formen f(x,φ,a,b,c...) där φ är en skalfaktor och a,b,c... är dimensionslösa parametrar, så kommer Gini-koefficienten att vara en funktion endast av a,b,c... . Till exempel, för exponentialfördelningen , som är en funktion av endast x och en skalparameter, är Gini-koefficienten en konstant, lika med 1/2.

För vissa funktionella former kan Gini-indexet beräknas explicit. Till exempel, om y följer en log-normalfördelning med standardavvikelsen för loggar lika med $\sigma$ , då $G=\operatörsnamn {erf} \left({ \frac {\sigma }{2}}\right)$ där $\operatorname {erf}$ är felfunktionen (eftersom ${\displaystyle G=2\Phi \ left({\frac {\sigma }{\sqrt {2}}}\right)-1} ,$ där $\Phi$ är den kumulativa fördelningsfunktionen för en standardnormalfördelning). I tabellen nedan visas några exempel på sannolikhetstäthetsfunktioner med stöd på ${\displaystyle [0,\infty )} .$ Dirac-deltatfördelningen representerar fallet där alla har samma förmögenhet (eller inkomst); det innebär inga variationer mellan inkomster.

Funktion för inkomstfördelning	PDF(x)	Gini koefficient
Dirac delta funktion	$\delta (x-x_{0}),\,x_{0}>0$	0
Jämn fördelning	${\begin{cases}{\frac {1}{ba}}&a\leq x\leq b\\0&\mathrm {annat} \end{cases}}$	${\frac {(ba)}{3(b+a)}}$
Exponentiell fördelning	$\lambda e^{-x\lambda },\,\,x>0$	$\displaystyle 1/2$
Log-normalfördelning	${\frac {1}{x\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {\ln \,(x)-\mu }{\sigma }}\right)^{2}}$	${\textrm {erf}}(\sigma /2)=2\Phi \left({\frac {\sigma }{\sqrt {2 }}}\right)-1$
Pareto distribution	${\begin{cases}{\frac {\alpha k^{\alpha }}{x^{\alpha +1}}}&x\geq k\\0&x<k\end{cases}}$	$\displaystyle {\begin{cases}1&0<\alpha <1\\{\frac {1}{2\alpha -1}}&\alpha \geq 1\end{case}}}$
Chi distribution	$f(x;k)={\begin{cases }{\dfrac {x^{k-1}e^{-x^{2}/2}}{2^{k/2-1}\Gamma \left({\frac {k}{2}} \right)}},&x\geq 0\\0,&x<0\end{cases}}$	$(-1)^{k}\left\|I_{-1}(k,{\tfrac {1}{2}})\right\|$
Chi-kvadratfördelning	${\frac {2^{-k/2}e^{-x/2}x^{k/ 2-1}}{\Gamma (k/2)}}$	${\frac {2\,\Gamma \left({\frac {1+k}{2}}\right)}{k\ ,\Gamma (k/2){\sqrt {\pi }}}}$
Gammafördelning	${\frac {e^{-x/\theta }x^{k-1}\theta ^{-k}}{\Gamma (k)}}$	${\frac {\Gamma \left({\frac {2k+1}{2}}\right)}{k\,\Gamma (k ){\sqrt {\pi }}}}$
Weibull distribution	${\frac {k}{\lambda }}\,\left({\frac {x}{\lambda }}\right) ^{k-1}e^{-(x/\lambda )^{k}}$	$1-2^{-1/k}$
Betadistribution	${\frac {x^{\alpha -1}(1-x)^{\beta -1}}{B(\ alfa ,\beta )}}$	$\left({\frac {2}{\alpha }}\right){\frac { B(\alpha +\beta ,\alpha +\beta )}{B(\alpha ,\alpha )B(\beta ,\beta )}}$
Logistisk distribution	${\frac {(\beta /\alpha )(x/\alpha )^{\beta -1 }}{\left(1+(x/\alpha )^{\beta }\right)^{2}}}$	$1/\beta$

$\Gamma (\,)$ är gammafunktionen
$B(\,)$ är betafunktionen
$I_{k}(\,)$ är den Regularized incomplete beta-funktionen

Andra tillvägagångssätt

Ibland är hela Lorenz-kurvan inte känd, och endast värden vid vissa intervall anges. I så fall kan Gini-koefficienten approximeras med hjälp av olika tekniker för att interpolera de saknade värdena på Lorenz-kurvan. Om ( X _k , Y _k ) är de kända punkterna på Lorenz-kurvan, med X _k indexerad i stigande ordning ( X _{k – 1} < X _k ), så att:

₀ X _k är den kumulerade andelen av populationsvariabeln, för k = 0,..., n , med X = 0, X _n = 1.
₀ Y _k är den ackumulerade andelen av inkomstvariabeln, för k = 0,..., n , med Y = 0, Y _n = 1.
Y _k ska indexeras i icke-minskande ordning ( Y _k > Y _{k – 1} )

Om Lorenz-kurvan är approximerad på varje intervall som en linje mellan på varandra följande punkter, så kan arean B approximeras med trapetser och:

G_{1}=1-\summa _{k=1}^{n} (X_{k}-X_{k-1})(Y_{k}+Y_{k-1})

är den resulterande approximationen för G. Mer exakta resultat kan erhållas med andra metoder för att approximera arean B, som att approximera Lorenz-kurvan med en kvadratisk funktion över par av intervall eller bygga en lämplig jämn approximation till den underliggande fördelningsfunktionen som matchar den kända data. Om populationsmedelvärdena och gränsvärdena för varje intervall också är kända kan dessa också ofta användas för att förbättra approximationens noggrannhet.

Gini-koefficienten som beräknas från ett urval är en statistik, och dess standardfel, eller konfidensintervall för populationens Gini-koefficient, bör rapporteras. Dessa kan beräknas med hjälp av bootstrap -tekniker, matematiskt komplicerade och beräkningskrävande även i en tid av snabba datorer. Ekonomen Tomson Ogwang effektiviserade processen genom att sätta upp en "trick-regressionsmodell" där respektive inkomstvariabler i urvalet rangordnas, där den lägsta inkomsten tilldelas rang 1. Modellen uttrycker sedan rangen (beroende variabel) som summan av en konstant A och en normal felterm vars varians är omvänt proportionell mot y _k :

k=A+\ N(0,s^{2}/y_{k})

Således kan G uttryckas som en funktion av den viktade minsta kvadrat-uppskattningen av konstanten A och att denna kan användas för att påskynda beräkningen av jackknife -estimatet för standardfelet. Ekonomen David Giles hävdade att standardfelet för skattningen av A kan användas för att härleda uppskattningen av G direkt utan att använda en jackkniv. Denna metod kräver endast användning av vanlig minsta kvadratregression efter att provdata har beställts. Resultaten jämförs positivt med uppskattningarna från jackkniven med överensstämmelse som förbättras med ökande urvalsstorlek.

Det har dock hävdats att detta beror på modellens antaganden om felfördelningarna och feltermernas oberoende. Dessa antaganden är ofta inte giltiga för verkliga datamängder. Det pågår fortfarande debatt kring detta ämne.

Guillermina Jasso och Angus Deaton föreslog oberoende av varandra följande formel för Gini-koefficienten:

G={\frac {N+1}{N-1}}-{\ frac {2}{N(N-1)\mu }}(\summa _{i=1}^{n}P_{i}X_{i})

där $\mu$ är befolkningens medelinkomst, P _i är inkomstgraden P för person i, med inkomst X, så att den rikaste personen får en rang av 1 och den fattigaste en rang av N . Detta ger i praktiken högre vikt till fattigare människor i inkomstfördelningen, vilket gör att Gini kan uppfylla överföringsprincipen . Observera att Jasso-Deaton-formeln skalar om koefficienten så att dess värde är ett om alla $X_{i}$ är noll utom en. Notera dock Allisons svar om behovet av att dividera med N² istället.

FAO förklarar en annan version av formeln.

Generaliserade ojämlikhetsindex

Gini-koefficienten och andra standardojämlikhetsindex reduceras till en vanlig form. Perfekt jämlikhet – frånvaron av ojämlikhet – existerar när och endast när ojämlikhetsförhållandet, ${\displaystyle r_{j}=x_{j}/{\overline {x}}}, är$ lika med 1 för alla j-enheter i någon population (till exempel, det finns perfekt inkomstlikhet när allas inkomst $x_{j}$ är lika med medelinkomsten ${\overline {x}}$ , så att $r_{j}=1$ för alla). Mått på ojämlikhet är alltså mått på de genomsnittliga avvikelserna för $r_{j}=1$ från 1; ju större genomsnittlig avvikelse, desto större ojämlikhet. Baserat på dessa observationer har ojämlikhetsindexen denna vanliga form:

{\text{Ojämlikhet}}=\summa _{j}p_{j}\,f(r_{j}),

där p _j viktar enheterna med deras befolkningsandel, och f ( r _j ) är en funktion av avvikelsen för varje enhets r _j från 1, punkten för likhet. Insikten i detta generaliserade ojämlikhetsindex är att ojämlikhetsindex skiljer sig eftersom de använder olika funktioner för avståndet mellan ojämlikhetskvoterna (rj) från 1 _.

Av inkomstfördelningar

Härledning av Lorenzkurvan och Gini-koefficienten för global inkomst 2011

Gini-inkomstkoefficienter beräknas på en marknadsmässig inkomst och en disponibel inkomstbasis. Gini-koefficienten på marknadsinkomst – ibland kallad en Gini-koefficient före skatt – beräknas på inkomst före skatter och transfereringar. Den mäter ojämlikhet i inkomst utan att beakta effekten av skatter och sociala utgifter som redan finns i ett land. Gini-koefficienten på disponibel inkomst – ibland kallad Gini-koefficienten efter skatt – beräknas på inkomst efter skatter och transfereringar. Den mäter ojämlikhet i inkomst efter att ha beaktat effekten av skatter och sociala utgifter som redan finns i ett land.

För OECD- länderna under perioden 2008–2009 varierade Gini-koefficienten (före skatter och transfereringar) för en total befolkning mellan 0,34 och 0,53, med Sydkorea den lägsta och Italien den högsta. Gini-koefficienten (efter skatter och transfereringar) för en total befolkning varierade mellan 0,25 och 0,48, med Danmark den lägsta och Mexiko den högsta. För USA, landet med den största befolkningen bland OECD-länderna, var Gini-indexet före skatt 0,49 och Gini-indexet efter skatt var 0,38 2008–2009. OECD-genomsnittet för den totala befolkningen i OECD-länderna var 0,46 för Gini-index för inkomst före skatt och 0,31 för Gini-index för inkomst efter skatt. Skatter och sociala utgifter som var på plats under perioden 2008–2009 i OECD-länder minskade avsevärt den faktiska inkomstskillnaden, och generellt sett uppnår "Europeiska länder - särskilt nordiska och kontinentala välfärdsstater - lägre nivåer av inkomstskillnader än andra länder."

Att använda Gini kan hjälpa till att kvantifiera skillnader i välfärds- och kompensationspolicyer och filosofier. Man bör dock komma ihåg att Gini-koefficienten kan vara missvisande när den används för att göra politiska jämförelser mellan stora och små länder eller de med olika invandringspolitik (se avsnittet om begränsningar ).

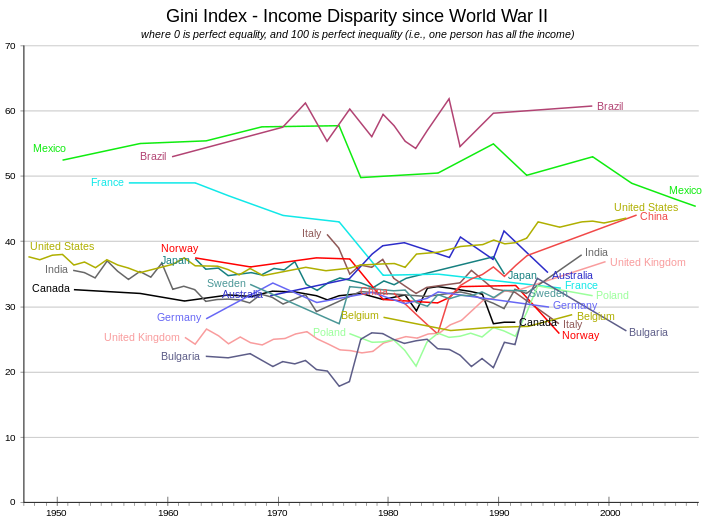
Gini-koefficienten för hela världen har av olika parter uppskattats till mellan 0,61 och 0,68. Grafen visar värdena uttryckta i procent i deras historiska utveckling för ett antal länder.

Regionala inkomst Gini-index

Enligt UNICEF hade Latinamerika och den karibiska regionen världens högsta nettoinkomst Gini-index på 48,3, på ett oviktat genomsnitt 2008. De återstående regionala genomsnitten var: Afrika söder om Sahara (44,2), Asien (40,4), Mellanöstern och Nordafrika (39,2), Östeuropa och Centralasien (35,4) och höginkomstländer (30,9). Med samma metod påstås USA ha ett Gini-index på 36, medan Sydafrika hade högsta inkomst Gini-index på 67,8.

Världsinkomst Gini-index sedan 1800-talet

Om man tar inkomstfördelningen för alla människor, har den globala inkomstskillnaden ökat konstant sedan början av 1800-talet. Det skedde en stadig ökning av Gini-poängen för global inkomstojämlikhet från 1820 till 2002, med en betydande ökning mellan 1980 och 2002. Denna trend verkar ha nått sin topp och inlett en vändning med snabb ekonomisk tillväxt i tillväxtekonomier, särskilt i de stora befolkningarna i BRIC- länder.

Tabellen nedan visar de uppskattade Gini-koefficienterna för världsinkomsten under de senaste 200 åren, beräknade av Milanovic.

Inkomst Gini-koefficient - Världen, 1820–2005
År	Världens Gini-koefficienter
1820	0,43
1850	0,53
1870	0,56
1913	0,61
1929	0,62
1950	0,64
1960	0,64
1980	0,66
2002	0,71
2005	0,68

Mer detaljerade data från liknande källor visar en kontinuerlig nedgång sedan 1988. Detta tillskrivs globaliseringen som ökar inkomsterna för miljarder fattiga människor, mestadels i länder som Kina och Indien. Utvecklingsländer som Brasilien har också förbättrat grundläggande tjänster som hälsovård, utbildning och sanitet; andra som Chile och Mexiko har antagit en mer progressiv skattepolitik .

Inkomst Gini-koefficient - Världen, 1988–2013
År	Världens Gini-koefficienter
1988	0,80
1993	0,76
1998	0,74
2003	0,72
2008	0,70
2013	0,65

Av social utveckling

Gini-koefficienten används i stor utsträckning inom så olika områden som sociologi, ekonomi, hälsovetenskap, ekologi, teknik och jordbruk. Till exempel, inom samhällsvetenskap och ekonomi, förutom inkomst Gini-koefficienter, har forskare publicerat utbildning Gini-koefficienter och möjlighet Gini-koefficienter.

Utbildning

Utbildning Gini-index uppskattar ojämlikheten i utbildning för en given befolkning. Det används för att urskilja trender i social utveckling genom utbildningsnivå över tid. En studie i 85 länder av tre ekonomer från Världsbanken, Vinod Thomas, Yan Wang och Xibo Fan, uppskattade att Mali hade det högsta utbildnings-Gini-indexet på 0,92 år 1990 (vilket innebär mycket hög ojämlikhet i utbildningsnivåer över hela befolkningen), medan USA hade lägst utbildningsojämlikhet Gini-index på 0,14. Mellan 1960 och 1990 hade Kina, Indien och Sydkorea den snabbaste nedgången i Gini-index för ojämlikhet i utbildning. De hävdar också att utbildningens Gini-index för USA ökade något under perioden 1980–1990.

Även om Indiens Gini-index för utbildning har sjunkit från 1960 till 1990, har de flesta av befolkningen fortfarande inte fått någon utbildning, medan 10 procent av befolkningen fick mer än 40 % av de totala utbildningstimmarna i landet. Det innebär att en stor del av kapabla barn i landet inte får det stöd som krävs för att de ska kunna bli positiva bidragsgivare till samhället. Detta kommer att leda till en dödviktsförlust för det nationella samhället eftersom det finns många människor som är underutvecklade och underutnyttjade.

Möjlighet

I likhet med Gini-inkomstkoefficienten mäter Gini-möjlighetskoefficienten ojämlikhet i möjligheter. Konceptet bygger på Amartya Sens förslag att ojämlikhetskoefficienter för social utveckling bör baseras på processen att utöka människors valmöjligheter och förbättra deras förmåga, snarare än på processen att minska inkomstskillnaderna. Kovacevic, i en genomgång av Gini-möjlighetskoefficienten, förklarade att koefficienten uppskattar hur väl ett samhälle gör det möjligt för sina medborgare att nå framgång i livet där framgången är baserad på en persons val, ansträngningar och talanger, inte hans bakgrund definierad av en uppsättning av förutbestämda omständigheter vid födseln, såsom kön, ras, födelseort, förälders inkomst och omständigheter utanför den personens kontroll.

2003 rapporterade Roemer att Italien och Spanien uppvisade det största Gini-indexet för ojämlikhet bland avancerade ekonomier.

Inkomströrlighet

1978 introducerade Anthony Shorrocks ett mått baserat på inkomst Gini-koefficienter för att uppskatta inkomströrlighet. Detta mått, generaliserat av Maasoumi och Zandvakili, kallas nu allmänt för Shorrocks index , ibland som Shorrocks mobilitetsindex eller Shorrocks rigidity index. Den försöker uppskatta om Gini-koefficienten för inkomstojämlikhet är permanent eller tillfällig och i vilken utsträckning ett land eller en region möjliggör ekonomisk rörlighet till sina invånare så att de kan flytta från en (t.ex. de lägsta 20 %) inkomstkvantilerna till en annan (t.ex. 20 %) över tiden. Med andra ord jämför Shorrocks-index ojämlikhet mellan kortsiktiga inkomster, såsom hushållens årsinkomst, med ojämlikhet i långsiktiga inkomster, såsom 5-åriga eller 10-åriga totala inkomster för samma hushåll.

Shorrocks index beräknas på flera olika sätt, ett vanligt tillvägagångssätt är utifrån förhållandet mellan inkomst Gini-koefficienter mellan kortsiktigt och långsiktigt för samma region eller land.

En studie från 2010 som använder socialförsäkringsinkomstdata för USA sedan 1937 och Gini-baserade Shorrocks index drar slutsatsen att inkomströrlighet i USA har haft en komplicerad historia, främst på grund av massinflödet av kvinnor till den amerikanska arbetskraften efter världskriget II. Inkomstskillnaderna och inkomströrligheten har varit olika för manliga och kvinnliga arbetare mellan 1937 och 2000-talet. När män och kvinnor betraktas tillsammans, innebär de Gini-koefficientbaserade Shorrocks-indextrenderna att långsiktig inkomstskillnad har minskat avsevärt bland alla arbetare, under de senaste decennierna för USA. Andra forskare, som bara använder 1990-talsdata eller andra korta perioder, har kommit till andra slutsatser. Till exempel drar Sastre och Ayala slutsatsen från sin studie av inkomst Gini-koefficientdata mellan 1993 och 1998 för sex utvecklade ekonomier att Frankrike hade minst inkomströrlighet, Italien högst och USA och Tyskland mellanliggande nivåer av inkomströrlighet under dessa fem år .

Funktioner

Gini-koefficienten har egenskaper som gör den användbar som ett mått på spridning i en befolkning, och i synnerhet ojämlikheter.

Begränsningar

Gini-koefficienten är ett relativt mått. Gini-koefficienten för ett utvecklingsland kan stiga (på grund av ökande inkomstskillnad) även när antalet människor i absolut fattigdom minskar. Detta beror på att Gini-koefficienten mäter relativ, inte absolut, rikedom. Förändrad inkomstojämlikhet, mätt med Gini-koefficienter, kan bero på strukturella förändringar i ett samhälle som växande befolkning (ökade födelsetal, åldrande befolkningar, ökade skilsmässor, familjehushåll som splittras i kärnfamiljer, emigration, immigration ) och inkomströrlighet . Gini-koefficienter är enkla, och denna enkelhet kan leda till förbiseenden och kan förvirra jämförelsen av olika populationer; till exempel, medan både Bangladesh (inkomst per capita på 1 693 USD) och Nederländerna (inkomst per capita på 42 183 USD) hade en Gini-inkomstkoefficient på 0,31 2010, är livskvaliteten, de ekonomiska möjligheterna och den absoluta inkomsten i dessa länder väldigt olika, dvs länder kan ha identiska Gini-koefficienter, men skiljer sig mycket åt i rikedom. Basförnödenheter kan vara tillgängliga för alla i en utvecklad ekonomi, medan i en outvecklad ekonomi med samma Gini-koefficient kan basförnödenheter vara otillgängliga för de flesta eller ojämlikt tillgängliga på grund av lägre absolut rikedom.

Tabell A. Olika inkomstfördelningar med samma Gini-index
Hushållsgrupp	Land A årsinkomst ($)	Land B årsinkomst ($)
1	20 000	9 000
2	30 000	40 000
3	40 000	48 000
4	50 000	48 000
5	60 000	55 000
Total inkomst	200 000 USD	200 000 USD
Countrys Gini	0,2	0,2

Olika inkomstfördelningar med samma Gini-koefficient

Även när den totala inkomsten för en befolkning är densamma, kan i vissa situationer två länder med olika inkomstfördelningar ha samma Gini-index (t.ex. fall då inkomst-Lorenz-kurvorna korsar varandra). Tabell A illustrerar en sådan situation. Båda länderna har en Gini-koefficient på 0,2, men den genomsnittliga inkomstfördelningen för hushållsgrupper är olika. Som ett annat exempel, i en befolkning där de lägsta 50 % av individerna inte har någon inkomst, och de andra 50 % har samma inkomst, är Gini-koefficienten 0,5; För en annan befolkning där de lägsta 75 % av människorna har 25 % av inkomsten och de översta 25 % har 75 % av inkomsten, är Gini-indexet också 0,5. Ekonomier med liknande inkomster och Gini-koefficienter kan ha väldigt olika inkomstfördelningar. Bellù och Liberati hävdar att det inte alltid är möjligt att rangordna inkomstskillnader mellan två populationer baserat på deras Gini-index. På liknande sätt illustrerar beräkningssamhällsvetaren Fabian Stephany att inkomstojämlikhet inom befolkningen, t.ex. i specifika socioekonomiska grupper i samma ålder och utbildning, också förblir oupptäckta av konventionella Gini-index.

Extrem ojämlikhet i välstånd, men ändå låginkomst Gini-koefficient

Ett Gini-index innehåller inte information om absoluta nationella eller personliga inkomster. Populationer kan samtidigt ha mycket låga inkomster Gini-index och mycket höga Gini-index. Genom att mäta ojämlikhet i inkomst ignorerar Gini den differentiella effektiviteten i användningen av hushållsinkomst. Genom att ignorera rikedom (förutom när den bidrar till inkomster) kan Gini skapa sken av ojämlikhet när de jämförda människorna befinner sig i olika skeden av sitt liv. Rika länder som Sverige kan uppvisa en låg Gini-koefficient för den disponibla inkomsten på 0,31 och därigenom verka lika, men har en mycket hög Gini-koefficient för förmögenhet på 0,79 till 0,86, vilket tyder på en extremt ojämn förmögenhetsfördelning i samhället. Dessa faktorer bedöms inte i inkomstbaserad Gini.

Tabell B. Samma inkomstfördelning, men olika Gini-index
Hushållsnummer	Lands årsinkomst ($)	Hushållens sammanlagda nummer	Land A kombinerad årsinkomst ($)
1	20 000	1 & 2	50 000
2	30 000	1 & 2	50 000
3	40 000	3 & 4	90 000
4	50 000	3 & 4	90 000
5	60 000	5 & 6	130 000
6	70 000	5 & 6	130 000
7	80 000	7 & 8	170 000
8	90 000	7 & 8	170 000
9	120 000	9 och 10	270 000
10	150 000	9 och 10	270 000
Total inkomst	710 000 USD		710 000 USD
Countrys Gini	0,303		0,293

Små urvalsbias – glest befolkade regioner har mer sannolikt låg Gini-koefficient

Gini-index har en nedåtgående förspänning för små populationer. Län eller stater eller länder med liten befolkning och mindre olika ekonomier kommer att tendera att rapportera små Gini-koefficienter. För ekonomiskt olika stora befolkningsgrupper förväntas en mycket högre koefficient än för var och en av dess regioner. Om man till exempel tar världsekonomin som helhet och inkomstfördelningen för alla människor, uppskattar olika forskare att det globala Gini-indexet ligger mellan 0,61 och 0,68. Som med andra ojämlikhetskoefficienter påverkas Gini-koefficienten av mätningarnas granularitet . Till exempel kommer fem 20%-kvantiler (låg granularitet) vanligtvis att ge en lägre Gini-koefficient än tjugo 5% kvantiler (hög granularitet) för samma fördelning. Philippe Monfort har visat att användning av inkonsekvent eller ospecificerad granularitet begränsar användbarheten av Gini-koefficientmätningar.

Gini-koefficientmåttet ger olika resultat när det tillämpas på individer istället för hushåll, för samma ekonomi och samma inkomstfördelningar. Om hushållsdata används beror det uppmätta värdet av inkomst Gini på hur hushållet definieras. Jämförelsen är inte meningsfull när olika populationer inte mäts med konsekventa definitioner.

Deininger och Squire (1996) visar att inkomst Gini-koefficienten baserad på individuell inkomst snarare än hushållsinkomst är annorlunda. Till exempel, för USA, fann de att det individuella inkomstbaserade Gini-indexet var 0,35, medan det för Frankrike var 0,43. Enligt deras individfokuserade metod hade Sydafrika världens högsta Gini-koefficient på 0,62 i de 108 länder de studerade, Malaysia hade Asiens högsta Gini-koefficient på 0,5, Brasilien högst på 0,57 i Latinamerika och Karibien och Turkiet. den högsta med 0,5 i OECD-länder.

Tabell C. Hushållens penninginkomstfördelningar och Gini Index, USA
Inkomstklass (i 2010 justerade dollar)	% av befolkningen 1979	% av befolkningen 2010
Under $15 000	14,6 %	13,7 %
$15 000 – $24 999	11,9 %	12,0 %
$25 000 – $34 999	12,1 %	10,9 %
$35 000 – $49 999	15,4 %	13,9 %
50 000 - 74 999 $	22,1 %	17,7 %
$75 000 – $99 999	12,4 %	11,4 %
100 000 - 149 999 $	8,3 %	12,1 %
150 000 - 199 999 $	2,0 %	4,5 %
$200 000 och över	1,2 %	3,9 %
Totalt hushåll	80 776 000	118 682 000
USA:s Gini före skatt	0,404	0,469

Gini-koefficienten kan inte urskilja effekterna av strukturella förändringar i populationer

För att utvidga vikten av livslängdsmått, ignorerar Gini-koefficienten som en punktuppskattning av jämlikhet vid en viss tidpunkt livslängdsförändringar i inkomst. Vanligtvis kommer ökningar av andelen unga eller gamla medlemmar i ett samhälle att driva på uppenbara förändringar i jämställdhet helt enkelt för att människor generellt har lägre inkomster och förmögenhet när de är unga än när de är gamla. På grund av detta kan faktorer som åldersfördelning inom en befolkning och rörlighet inom inkomstklasser skapa sken av ojämlikhet när ingen existerar, med hänsyn tagen till demografiska effekter. En given ekonomi kan alltså ha en högre Gini-koefficient vid vilken tidpunkt som helst jämfört med en annan, medan Gini-koefficienten beräknad över individers livsinkomst är lägre än den till synes mer lika (vid en given tidpunkt) ekonomins. ^{[ förtydligande behövs ]} I grund och botten är det viktiga inte bara ojämlikheten under ett visst år utan fördelningens sammansättning över tiden.

Miljardären Thomas Kwok hävdade att inkomst Gini-koefficienten för Hongkong har varit hög (0,434 2010), delvis på grund av strukturella förändringar i dess befolkning. Under de senaste decennierna har Hongkong sett ett ökande antal små hushåll, äldre hushåll och äldre som bor ensamma. Den sammanlagda inkomsten är nu uppdelad på fler hushåll. Många äldre bor separat från sina barn i Hong Kong. Dessa sociala förändringar har orsakat betydande förändringar i hushållens inkomstfördelning. Gini-inkomstkoefficienten, hävdar Kwok, urskiljer inte dessa strukturella förändringar i sitt samhälle. Hushållens inkomstfördelning för USA, sammanfattad i tabell C i detta avsnitt, bekräftar att denna fråga inte är begränsad till bara Hongkong. Enligt US Census Bureau, mellan 1979 och 2010, upplevde befolkningen i USA strukturella förändringar i hushållen överlag; inkomsten för alla inkomstgrupper ökade i inflationsjusterade termer, hushållens inkomstfördelningar skiftade över tid till högre inkomstklasser, medan inkomst Gini-koefficienten ökade.

En annan begränsning av Gini-koefficienten är att den inte är ett korrekt mått på jämlikhet , eftersom den bara mäter inkomstspridning. Anta till exempel att två lika jämlika länder driver olika invandringspolitik. I så fall kommer det land som accepterar en högre andel låginkomsttagare eller fattiga migranter att rapportera en högre Gini-koefficient och kan därför uppvisa större inkomstskillnader.

Oförmåga att värdera fördelar och inkomster från informell ekonomi påverkar Gini-koefficientens noggrannhet

Vissa länder delar ut förmåner som är svåra att värdera. Länder som tillhandahåller subventionerat boende, sjukvård, utbildning eller andra sådana tjänster är svåra att objektivt värdera, eftersom det beror på förmånens kvalitet och omfattning. I avsaknad av en fri marknad är det subjektivt att värdera dessa inkomstöverföringar som hushållsinkomst. Den teoretiska modellen för Gini-koefficienten är begränsad till att acceptera korrekta eller felaktiga subjektiva antaganden.

I försörjningsdrivna och informella ekonomier kan människor ha betydande inkomster i andra former än pengar, till exempel genom subsistensjordbruk eller byteshandel . Dessa inkomster tenderar att tillfalla den del av befolkningen som ligger under fattigdomsgränsen eller mycket fattiga i länder med framväxande och övergångsekonomi, såsom de i Afrika söder om Sahara, Latinamerika, Asien och Östeuropa. Informell ekonomi står för över hälften av den globala sysselsättningen och så mycket som 90 procent av sysselsättningen i några av de fattigare länderna söder om Sahara med höga officiella Gini-ojämlikhetskoefficienter. Schneider et al., i sin studie från 2010 av 162 länder, rapporterar att cirka 31,2 %, eller cirka 20 biljoner dollar, av världens BNP är informell. I utvecklingsländer dominerar den informella ekonomin för alla inkomstklasser utom de rikare, urbana övre inkomstgrupperna. Även i utvecklade ekonomier är 8 % (USA) till 27 % (Italien) av varje nations BNP informell. Den resulterande informella inkomsten dominerar som en försörjningsverksamhet för dem i de lägsta inkomstklasserna. Värdet och fördelningen av inkomsterna från informell eller underjordisk ekonomi är svår att kvantifiera, vilket gör uppskattningar av verkliga Gini-koefficienter svåra. Olika antaganden och kvantifieringar av dessa inkomster kommer att ge olika Gini-koefficienter.

Gini har också vissa matematiska begränsningar. Det är inte additivt och olika uppsättningar av människor kan inte beräknas i medeltal för att få fram Gini-koefficienten för alla personer i uppsättningarna.

Alternativ

Med tanke på Gini-koefficientens begränsningar används andra statistiska metoder i kombination eller som ett alternativt mått på befolkningsspridningen. Till exempel används entropimått ofta (t.ex. Atkinsonindex eller Theil Index och Mean log deviation som specialfall av det generaliserade entropiindexet ). Dessa åtgärder försöker jämföra fördelningen av resurser av intelligenta agenter på marknaden med en maximal entropi slumpmässig fördelning , vilket skulle inträffa om dessa medel agerade som icke-interagerande partiklar i ett slutet system enligt statistisk fysiks lagar.

Förhållande till andra statistiska mått

Det finns ett sammanfattande mått på den diagnostiska förmågan hos ett binärt klassificeringssystem som också kallas Gini-koefficienten , som definieras som två gånger arean mellan mottagarens operationskarakteristik (ROC) kurva och dess diagonal. Det är relaterat till AUC- måttet ( Area Under ROC-kurvan) på prestanda som ges av $AUC=(G+1)/2$ och till Mann–Whitney U . Även om båda Gini-koefficienterna definieras som områden mellan vissa kurvor och delar vissa egenskaper, finns det inget enkelt direkt samband mellan Gini-koefficienten för statistisk spridning och Gini-koefficienten för en klassificerare.

Gini-indexet är också relaterat till Pietra-indexet - som båda mäter statistisk heterogenitet och är härledda från Lorenz-kurvan och den diagonala linjen.

används invers Simpsons index ${\displaystyle 1/\lambda } för att kvantifiera mångfald, och detta bör inte förväxlas med$ Simpson-indexet $\lambda$ . Dessa indikatorer är relaterade till Gini. Det omvända Simpson-indexet ökar med mångfalden, till skillnad från Simpson-indexet och Gini-koefficienten, som minskar med mångfalden. Simpson-indexet ligger i intervallet [0, 1], där 0 betyder maximal och 1 betyder minsta mångfald (eller heterogenitet). Eftersom diversitetsindex vanligtvis ökar med ökande heterogenitet, omvandlas Simpson-indexet ofta till invers Simpson, eller med hjälp av komplementet $1-\lambda$ , känt som Gini-Simpson Index.

Gini-koefficienter för förmoderna samhällen

Under de senaste decennierna har forskare försökt uppskatta Gini-koefficienter för samhällen före 1900-talet. I avsaknad av hushållsinkomstundersökningar och inkomstskatter har forskare förlitat sig på proxyvariabler. Dessa inkluderar förmögenhetsskatter i medeltida europeiska stadsstater, mönster för jordägande i det romerska Egypten, variation av storleken på hus i samhällen från antikens Grekland till Aztekiska Mexiko, och arv och hemgift i det babyloniska samhället. Andra data dokumenterar inte direkt variationer i förmögenhet eller inkomst men är kända för att återspegla ojämlikhet, såsom förhållandet mellan hyror och löner eller mellan arbete och kapital.

Andra användningsområden

Även om Gini-koefficienten är mest populär inom ekonomi, kan den i teorin tillämpas inom alla vetenskapsområden som studerar en fördelning. Till exempel, inom ekologi, har Gini-koefficienten använts som ett mått på biologisk mångfald , där den kumulativa andelen arter plottas mot den kumulativa andelen individer. Inom hälsa har det använts som ett mått på ojämlikheten i hälsorelaterad livskvalitet i en befolkning. Inom utbildning har det använts som ett mått på universitetens ojämlikhet. Inom kemin har det använts för att uttrycka selektiviteten hos proteinkinashämmare mot en panel av kinaser. Inom tekniken har det använts för att utvärdera rättvisan som uppnås av Internetroutrar vid schemaläggning av paketöverföringar från olika trafikflöden.

Gini-koefficienten används ibland för att mäta den diskriminerande kraften hos ratingsystem i kreditriskhantering .

En studie från 2005 fick tillgång till amerikanska folkräkningsdata för att mäta ägande av hemdatorer och använde Gini-koefficienten för att mäta ojämlikheter mellan vita och afroamerikaner. Resultaten visade att även om de minskade totalt sett, var ojämlikheten i hemdatorägande betydligt mindre bland vita hushåll.

En peer-reviewed studie från 2016 med titeln Att använda Gini-koefficienten för att mäta ojämlikhet i deltagande i behandlingsfokuserade digitala hälso-sociala nätverk illustrerade att Gini-koefficienten var till hjälp och korrekt för att mäta förändringar i ojämlikhet, men som ett fristående mått misslyckades den med att införliva den övergripande nätverksstorleken .

Diskriminerande makt hänvisar till en kreditriskmodells förmåga att skilja mellan kunder som inte förfaller. Formeln ${\displaystyle G_{1}},$ i beräkningsavsnittet ovan, kan användas för den slutliga modellen och på den individuella modellfaktornivån för att kvantifiera den diskriminerande styrkan hos individuella faktorer. Det är relaterat till noggrannhetsförhållandet i populationsbedömningsmodeller.

Gini-koefficienten har också använts för att analysera ojämlikhet i dejtingappar .

Kaminskiy och Krivtsov utökade konceptet med Gini-koefficienten från ekonomi till tillförlitlighetsteori och föreslog en Gini-typ koefficient som hjälper till att bedöma graden av åldrande av icke-reparerbara system eller åldrande och föryngring av reparerbara system. Koefficienten är definierad mellan -1 och 1 och kan användas i både empiriska och parametriska livsfördelningar. Den tar negativa värden för klassen av minskande felfrekvensfördelningar och punktprocesser med minskande felintensitetsfrekvens och är positiv för de ökande felfrekvensfördelningarna och punktprocesser med ökande felintensitetsfrekvens. Värdet på noll motsvarar den exponentiella livsfördelningen eller den homogena poissonprocessen .

Se även

Vidare läsning

Amiel, Y.; Cowell, F.A. (1999). Funderar på ojämlikhet . Cambridge. ISBN 978-0-521-46696-7 .
Anand, Sudhir (1983). Ojämlikhet och fattigdom i Malaysia . New York: Oxford University Press. ISBN 978-0-19-520153-6 .
Brown, Malcolm (1994). "Att använda Gini-stilsindex för att utvärdera de rumsliga mönstren för hälsoutövare: Teoretiska överväganden och en tillämpning baserad på Alberta-data". Samhällsvetenskap & medicin . 38 (9): 1243–1256. doi : 10.1016/0277-9536(94)90189-9 . PMID 8016689 .
Chakravarty, S.R. (1990). Etiska sociala indexnummer . New York: Springer-Verlag. ISBN 978-0-387-52274-6 .
Deaton, Angus (1997). Analys av hushållsundersökningar . Baltimore MD: Johns Hopkins University Press. ISBN 978-0-585-23787-9 .
Dixon, Philip M.; Weiner, Jacob; Mitchell-Olds, Thomas; Woodley, Robert (1987). "Bootstrapping Gini-koefficienten för ojämlikhet". Ekologi . 68 (5): 1548–1551. doi : 10.2307/1939238 . JSTOR 1939238 . S2CID 84940050 .
Dorfman, Robert (1979). "En formel för Gini-koefficienten". Översikten av ekonomi och statistik . 61 (1): 146–149. doi : 10.2307/1924845 . JSTOR 1924845 .
Firebaugh, Glenn (2003). Den nya geografin för global inkomstojämlikhet . Cambridge, Massachusetts: Harvard University Press. ISBN 978-0-674-01067-3 .
Gastwirth, Joseph L. (1972). "Uppskattningen av Lorenz-kurvan och Gini-index". Översikten av ekonomi och statistik . 54 (3): 306–316. doi : 10.2307/1937992 . JSTOR 1937992 .
Giles, David (2004). "Beräkna ett standardfel för gini-koefficienten: några ytterligare resultat" ( PDF) . Oxford Bulletin of Economics and Statistics . 66 (3): 425–433. CiteSeerX 10.1.1.202.6462 . doi : 10.1111/j.1468-0084.2004.00086.x . S2CID 16972099 . Arkiverad från originalet (PDF) den 5 maj 2004.
Gini, Corrado (1912). Variabilitet och mutabilitet . Bibcode : 1912vamu.book.....G . Återtryckt i Pizetti, E.; Salvemini, T., red. (1955). Memorie di metodologica statistica . Rom: Libreria Eredi Virgilio Veschi.
Gini, Corrado (1921). "Mätning av inkomstskillnader" . The Economic Journal . 31 (121): 124–126. doi : 10.2307/2223319 . JSTOR 2223319 .
Giorgi, Giovanni Maria (1990). "Bibliografiskt porträtt av Gini-koncentrationsförhållandet" (PDF) . Metron . 48 : 183–231. Arkiverad från originalet (PDF) den 4 augusti 2016.
Karagiannis, E.; Kovacevic, M. (2000). "En metod för att beräkna Jackknife Variance Estimator för Gini-koefficienten". Oxford Bulletin of Economics and Statistics . 62 : 119-122. doi : 10.1111/1468-0084.00163 .
Mills, Jeffrey A.; Zandvakili, Sourushe (1997). "Statistisk slutledning via bootstrapping för mätningar av ojämlikhet" ( PDF) . Journal of Applied Econometrics . 12 (2): 133–150. CiteSeerX 10.1.1.172.5003 . doi : 10.1002/(SICI)1099-1255(199703)12:2<133::AID-JAE433>3.0.CO;2-H . hdl : 10419/186818 . JSTOR 2284908 . Arkiverad (PDF) från originalet den 18 juli 2012.
Modarres, Reza; Gastwirth, Joseph L. (2006). "En försiktig anmärkning om att uppskatta standardfelet för Gini-indexet för ojämlikhet". Oxford Bulletin of Economics and Statistics . 68 (3): 385–390. doi : 10.1111/j.1468-0084.2006.00167.x . S2CID 122716409 .
Morgan, James (1962). "Inkomstfördelningens anatomi". Översikten av ekonomi och statistik . 44 (3): 270–283. doi : 10.2307/1926398 . JSTOR 1926398 .
Ogwang, Tomson (2000). "En bekväm metod för att beräkna Gini-index och dess standardfel". Oxford Bulletin of Economics and Statistics . 62 : 123–129. doi : 10.1111/1468-0084.00164 .
Ogwang, Tomson (2004). "Beräkna ett standardfel för Gini-koefficienten: Några ytterligare resultat: Svara". Oxford Bulletin of Economics and Statistics . 66 (3): 435–437. doi : 10.1111/j.1468-0084.2004.00087.x . S2CID 122160535 .
Xu, Kuan (januari 2004). "Hur har litteraturen på Ginis index utvecklats under de senaste 80 åren?" (PDF) . Institutionen för ekonomi, Dalhousie University. Arkiverad från originalet (PDF) den 28 september 2006 . Hämtad 1 juni 2006 . {{ citera journal }} : Citera journal kräver |journal= ( hjälp ) Den kinesiska versionen av denna artikel finns i Xu, Kuan (2003). "Hur har litteraturen på Ginis index utvecklats under de senaste 80 åren?". China Economic Quarterly . 2 : 757-778.
Yitzhaki, Shlomo (1991). "Beräkna Jackknife Variance Estimators för parametrar för Gini-metoden". Journal of Business and Economic Statistics . 9 (2): 235–239. doi : 10.2307/1391792 . JSTOR 1391792 .

externa länkar

Deutsche Bundesbank: Dividerar bankerna låneportföljer? , 2005 (om användning av t.ex. Gini-koefficienten för riskvärdering av låneportföljer)
Forbes artikel, Till beröm av ojämlikhet
Mätning av mjukvaruprojektrisk med Gini-koefficienten, en tillämpning av Gini-koefficienten på programvara
Världsbanken: Mätning av ojämlikhet
Travis Hale, University of Texas Inequality Project: Theoretical Basics of Popular Inequality Measures , onlineberäkning av exempel: 1A , 1B
Artikel från The Guardian som analyserar ojämlikhet i Storbritannien 1974–2006
World Income Inequality Database
Inkomstfördelning och fattigdom i OECD-länder
USA:s inkomstfördelning: hur ojämlikt?