Stericerade 5-simplex

Ortogonala projektioner i A ₅ och A ₄ Coxeter plan
5-simplex	Stericerad 5-simplex
Steritruncated 5-simplex	Steriskantellerad 5-simplex
Stericantitruncated 5-simplex	Sterrunkat 5-simplex
Steriruncicantitruncated 5-simplex (Omnitruncicated 5-simplex)

I femdimensionell geometri är en stericated 5-simplex en konvex enhetlig 5-polytop med fjärde ordningens trunkationer ( sterication ) av den vanliga 5-simplexen .

Det finns sex unika sterikationer av 5-simplex, inklusive permutationer av trunkationer, kantelleringar och runcinationer. Den enklaste stericerade 5-simplexen kallas också en expanderad 5-simplex , med den första och sista noden ringade, för att kunna konstrueras av en expansionsoperation som tillämpas på den vanliga 5-simplexen. Den högsta formen, steriruncicantitruncated 5-simplex kallas enklare en omnitruncated 5-simplex med alla noder ringade.

Stericerad 5-simplex

Stericerad 5-simplex
Typ	Uniform 5-polytop
Schläfli symbol	2r2r{3,3,3,3} 2r{3 ^2,2 } = $2r\left\{{\begin{array}{l}3,3\\ 3,3\end{array}}\right\}$
Coxeter-Dynkin diagram	eller
4-ansikten	62	6+6 {3,3,3} 15+15 {}×{3,3} 20 {3}×{3}
Celler	180	60 {3,3} 120 {}×{3}
Ansikten	210	120 {3} 90 {4}
Kanter	120
Vertices	30
Vertex figur	Tetraedrisk antiprisma
Coxeter grupp	A ₅ × 2, [[3,3,3,3]], order 1440
Egenskaper	konvex , isogonal , isotoxal

En steriliserad 5-simplex kan konstrueras genom en expansionsoperation som tillämpas på den vanliga 5-simplexen , och kallas därför ibland för en expanderad 5-simplex . Den har 30 hörn , 120 kanter , 210 ytor (120 trianglar och 90 kvadrater ), 180 celler (60 tetraedrar och 120 triangulära prismor ) och 62 4-ytor (12 5-celler , 30 tetraedriska prismor och 3 duo 3- ).

Alternativa namn

Utökad 5-simplex
Sterikerat hexateron
Liten cellad dodecateron (Akronym: scad) (Jonathan Bowers)

Tvärsnitt

Det maximala tvärsnittet av det stericerade hexateronet med ett 4-dimensionellt hyperplan är en runcinerad 5-cell . Detta tvärsnitt delar upp det sterikerade hexateronet i två pentakorala hyperkupoler bestående av 6 5-celler , 15 tetraedriska prismor och 10 3-3 duoprismor vardera.

Koordinater

Topparna av det stericerade 5-simplexet kan konstrueras på ett hyperplan i 6-rum som permutationer av (0,1,1,1,1,2). Detta representerar den positiva ortanta aspekten av det stericerade 6-ortoplexet .

En andra konstruktion i 6-utrymme, från mitten av ett likriktat 6-ortoplex ges av koordinatpermutationer av:

(1,-1,0,0,0,0)

De kartesiska koordinaterna i 5-utrymmet för de normaliserade hörnen av ett ursprungscentrerat sterikerat hexateron är:

{\displaystyle \left(\pm 1,\ 0,\ ​​0,\ ​​0,\ ​​0\right)} ( ,

displaystyle \left(0,\ \pm 1,\ 0,\ ​​0,\ ​​0\right)}

\left(0,\ 0,\ ​​\pm 1,\ 0,\ ​​0\right)

\left(\pm 1/2,\ 0,\ ​​\pm 1/2,\ -{\sqrt {1 /8}},\ -{\sqrt {3/8}}\right)

{\displaystyle \left(\pm 1/ 2,\

\left(0,\ \pm 1/2,\ \pm 1/2,\ -{\sqrt {1/8}},\ {\sqrt {3/8}}\right)

\left(0,\ \pm 1/2,\ \pm 1/2,\ {\sqrt {1/8}},\ -{\sqrt {3/8}}\right)

\left(\pm 1/2,\ \pm 1/2,\ 0,\ \pm {\sqrt {1/2}},\ 0\right)

Rotsystem

Dess 30 hörn representerar rotvektorerna för den enkla Lie-gruppen A ₅ . Det är också vertexfiguren för 5-simplex honeycomb .

Bilder

ortografiska projektioner
Ett _k Coxeter-plan	En ₅	A ₄
Graf
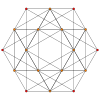
Dihedral symmetri	[6]	[[5]]=[10]
Ett _k Coxeter-plan	A ₃	A ₂
Graf
Dihedral symmetri	[4]	[[3]]=[6]

ortogonal projektion med [6] symmetri