Runcic 5-kuber

5-kub	Runcic 5-kub =
5-demikub =	Runcicantic 5-kub =
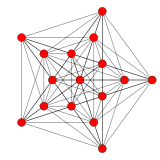Ortogonala projektioner i B 5 Coxeter-plan

I sexdimensionell geometri är en runcic 5-kub eller ( runcic 5-demicube , runcihalf 5-cube ) en konvex enhetlig 5-polytop . Det finns 2 runiska former för 5-kuben. Runcic 5-kuber har hälften av hörn av runcinerade 5-kuber .

Runcic 5-kub

Runcic 5-kub
Typ	enhetlig 5-polytop
Schläfli symbol	h 3 {4,3,3,3}
Coxeter-Dynkin diagram
4-ansikten	42
Celler	360
Ansikten	880
Kanter	720
Vertices	160
Vertex figur
Coxeter grupper	D5 , [3 2,1,1 ]
Egenskaper	konvex

Alternativa namn

• Kantellerad 5-demikub/demipenterakt
• Liten rhomberad hemipenteract (sirhin) (Jonathan Bowers)

kartesiska koordinater

De kartesiska koordinaterna för de 960 hörnen av en runkisk 5-kub centrerad vid ursprunget är koordinatpermutationer:

(±1,±1,±1,±3,±3)

med ett udda antal plustecken.

Bilder

ortografiska projektioner

Coxeter plan	B 5
Graf
Dihedral symmetri	[10/2]
Coxeter plan	D 5	D 4
Graf
Dihedral symmetri	[8]	[6]
Coxeter plan	D 3	A 3
Graf
Dihedral symmetri	[4]	[4]

Besläktade polytoper

Den har hälften av hörnen av den runcinerade 5-kuben , jämfört här i B5 Coxeter-planets projektioner:

Runcic 5-kub

Runcinerad 5-kub

Runcic n -kuber
n	4	5	6	7	8
[1 + ,4,3 n-2 ] = [3,3 n-3,1 ]	[1 + ,4,3 2 ] = [3,3 1,1 ]	[1 + ,4,3 3 ] = [3,3 2,1 ]	[1 + ,4,3 4 ] = [3,3 3,1 ]	[1 + ,4,3 5 ] = [3,3 4,1 ]	[1 + ,4,3 6 ] = [3,3 5,1 ]
Runcic figur
Coxeter	=	=	=	=	=
Schläfli	h 3 {4,3 2 }	h 3 {4,3 3 }	h 3 {4,3 4 }	h 3 {4,3 5 }	h 3 {4,3 6 }

Runcicantic 5-kub

Runcicantic 5-kub
Typ	enhetlig 5-polytop
Schläfli symbol	t 0,1,2 {3,3 2,1 } h 3 {4,3 3 }
Coxeter-Dynkin diagram
4-ansikten	42
Celler	360
Ansikten	1040
Kanter	1200
Vertices	480
Vertex figur
Coxeter grupper	D5 , [3 2,1,1 ]
Egenskaper	konvex

Alternativa namn

• Cantitruncated 5-demicube/demipenteract
• Stor romberad hemipenteract (girhin) (Jonathan Bowers)

kartesiska koordinater

De kartesiska koordinaterna för de 480 hörnen av en runcicantic 5-kub centrerad vid origo är koordinatpermutationer:

(±1,±1,±3,±5,±5)

med ett udda antal plustecken.

Bilder

ortografiska projektioner

Coxeter plan	B 5
Graf
Dihedral symmetri	[10/2]
Coxeter plan	D 5	D 4
Graf
Dihedral symmetri	[8]	[6]
Coxeter plan	D 3	A 3
Graf
Dihedral symmetri	[4]	[4]

Besläktade polytoper

Den har hälften av hörnen av den runcikantella 5-kuben , jämfört här i B5 Coxeter-planets projektioner:

Runcicantic 5-kub

Runcikantellerad 5-kub

Besläktade polytoper

Denna polytop är baserad på 5-demikuben , en del av en dimensionell familj av enhetliga polytoper som kallas demihyperkuber för att vara alternerande av hyperkubfamiljen .

Det finns 23 enhetliga 5-polytoper som kan konstrueras från D _5- symmetrin hos 5-demikuben, av vilka är unika för denna familj, och 15 delas inom 5- kubfamiljen .

Anteckningar

• HSM Coxeter :
  • HSM Coxeter, Regular Polytopes , 3:e upplagan, Dover New York, 1973
  •   Kaleidoscopes: Selected Writings of HSM Coxeter , redigerad av F. Arthur Sherk, Peter McMullen , Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
    • (Papper 22) HSM Coxeter, Regular and Semi Regular Polytopes I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Papper 23) HSM Coxeter, Regular and Semi-Regular Polytopes II , [Math. Zeit. 188 (1985) 559-591]
    • (Papper 24) HSM Coxeter, Regular and Semi-Regular Polytopes III , [Math. Zeit. 200 (1988) 3-45]
• Norman Johnson Uniform Polytopes , Manuscript (1991)
  • NW Johnson: Theory of Uniform Polytopes and Honeycombs , Ph.D.
• Klitzing, Richard. "5D enhetliga polytoper (polytera)" . x3o3o *b3x3o - sirhin, x3x3o *b3x3o - girhin

externa länkar

• Weisstein, Eric W. "Hypercube" . MathWorld .
• Polytoper av olika dimensioner
• Flerdimensionell ordlista