Rättade 5-ortoplexer

Ortogonala projektioner i A ₅ Coxeter-plan
5-kub	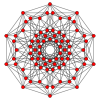Rättad 5-kub	Birektifierad 5-kub Birekifierad 5-ortoplex
5-ortoplex	Rättad 5-ortoplex	Birektifierad 5-kub Birekifierad 5-ortoplex

I femdimensionell geometri är en rätad 5-ortoplex en konvex enhetlig 5-polytop , som är en rätning av den vanliga 5-ortoplexen .

Det finns 5 grader av rätningar för varje 5-polytop, den nolla här är själva 5-ortoplexet och den fjärde och sista är 5-kuben . Vertices av det rätade 5-ortoplexet är belägna vid kant-centrum av 5-ortoplexet. Vertices av det birectifierade 5-ortoplexet är belägna i de triangulära ansiktscentrumen av 5-ortoplexet.

Rättad 5-ortoplex

Rättad pentacross
Typ	enhetlig 5-polytop
Schläfli symbol	t ₁ {3,3,3,4}
Coxeter-Dynkin diagram
Hyperceller	42 totalt: 10 {3,3,4} 32 t ₁ {3,3,3}
Celler	240 totalt: 80 {3,4} 160 {3,3}
Ansikten	400 totalt: 80+320 {3}
Kanter	240
Vertices	40
Vertex figur	Oktaedriskt prisma
Petrie polygon	Decagon
Coxeter grupper	BC ₅ , [3,3,3,4] D ₅ , [3 ^2,1,1 ]
Egenskaper	konvex

Dess 40 hörn representerar rotvektorerna för den enkla Lie-gruppen D ₅ . Topparna kan ses i 3 hyperplan , med de 10 hörnen rätade 5-cellsceller på motsatta sidor och 20 hörn av en runcinerad 5-cell som passerar genom mitten. När de kombineras med de 10 hörnen av 5-ortoplexet representerar dessa hörn de 50 rotvektorerna i B ₅ och C ₅ enkla Lie-grupper.

EL Elte identifierade den 1912 som en halvregelbunden polytop och identifierade den som Cr ₅¹ som en första rektifikation av en 5-dimensionell korspolytop .

Alternativa namn

korrigerad pentacross
rektifierad triacontiditeron (32-facetterad 5-polytop)

Konstruktion

Det finns två Coxeter-grupper associerade med den rätade pentacrossen , en med C ₅ eller [4,3,3,3] Coxeter-gruppen, och en lägre symmetri med två kopior av 16- cellsfasetter, alternerande, med D ₅ eller [ 3 ^2,1,1 ] Coxeter grupp.

kartesiska koordinater

Kartesiska koordinater för hörn av en rätad pentacross, centrerad vid origo, kantlängd ${\sqrt {2}}\$ är alla permutationer av:

(±1,±1,0,0,0)

Bilder

ortografiska projektioner
Coxeter plan	B ₅	B ₄ / D ₅	B ₃ / D ₄ / A ₂
Graf
Dihedral symmetri	[10]	[8]	[6]
Coxeter plan	B ₂	A ₃
Graf
Dihedral symmetri	[4]	[4]

Besläktade polytoper

Den rätade 5-ortoplexen är vertexfiguren för 5-demikubens honungskaka :

eller

Denna polytop är en av 31 enhetliga 5-polytoper som genereras från den vanliga 5-kuben eller 5-ortoplexen .

Anteckningar

HSM Coxeter :
- HSM Coxeter, Regular Polytopes , 3:e upplagan, Dover New York, 1973
- Kaleidoscopes: Selected Writings of HSM Coxeter , redigerad av F. Arthur Sherk, Peter McMullen , Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
  - (Papper 22) HSM Coxeter, Regular and Semi Regular Polytopes I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
  - (Papper 23) HSM Coxeter, Regular and Semi-Regular Polytopes II , [Math. Zeit. 188 (1985) 559-591]
  - (Papper 24) HSM Coxeter, Regular and Semi-Regular Polytopes III , [Math. Zeit. 200 (1988) 3-45]
Norman Johnson Uniform Polytopes , Manuscript (1991)
- NW Johnson: Theory of Uniform Polytopes and Honeycombs , Ph.D.
Klitzing, Richard. "5D enhetliga polytoper (polytera)" . o3x3o3o4o - råtta

externa länkar

Grundläggande konvexa regelbundna och enhetliga polytoper i dimensionerna 2–10
Familj	A _n	B _n	I ₂ (p) / D _n	E ₆ / E ₇ / E ₈ / F ₄ / G ₂	H _n
Vanlig polygon	Triangel	Fyrkant	p-gon	Sexhörning	Pentagon
Uniform polyeder	Tetraeder	Oktaeder • Kub	Demicube		Dodekaeder • Ikosaeder
Uniform polychoron	Pentachoron	16-celler • Tesseract	Demitesseract	24-celler	120-celler • 600-celler
Uniform 5-polytop	5-simplex	5-ortoplex • 5-kub	5-demikub
Uniform 6-polytop	6-simplex	6-ortoplex • 6-kub	6-demikub	1 ₂₂ • 2 ₂₁
Uniform 7-polytop	7-simplex	7-ortoplex • 7-kub	7-demikub	1 ₃₂ • 2 ₃₁ • 3 ₂₁
Uniform 8-polytop	8-simplex	8-ortoplex • 8-kub	8-demikub	1 ₄₂ • 2 ₄₁ • 4 ₂₁
Uniform 9-polytop	9-simplex	9-ortoplex • 9-kub	9-demikub
Uniform 10-polytop	10-simplex	10-ortoplex • 10-kub	10-demikub
Uniform n - polytop	n - simplex	n - ortoplex • n - kub	n - demikub	1 _k2 • 2 _k1 • k ₂₁	n - femkantig polytop
Ämnen: Polytopfamiljer • Vanlig polytop • Lista över vanliga polytoper och sammansättningar

B5 polytoper
β ₅	t ₁ β ₅	t ₂ γ ₅	t ₁ γ ₅	γ ₅	t _0,1 β5 _{_}	t _0,2 β ₅	t _1,2 β ₅
t _0,3 β5 _{_}	t _1,3 y ₅	t _1,2 y ₅	t _0,4 y ₅	t _0,3 y ₅	t _0,2 y ₅	t _0,1 y ₅	t _0,1,2 p5 _{_}
t _0,1,3 p5 _{_}	t _0,2,3 p5 _{_}	t _1,2,3 y ₅	t _0,1,4 p5 _{_}	t _0,2,4 y ₅	t _0,2,3 y ₅	t _0,1,4 y ₅	t _0,1,3 y ₅
t _0,1,2 y ₅	t _0,1,2,3 p5 _{_}	t _0,1,2,4 β5 _{_}	t _0,1,3,4 y ₅	t _0,1,2,4 y ₅	t _0,1,2,3 y ₅	t _0,1,2,3,4 y ₅