Röntgenkristallografi

En pulverröntgendiffraktometer i rörelse

Röntgenkristallografi är den experimentella vetenskapen som bestämmer den atomära och molekylära strukturen hos en kristall , där den kristallina strukturen får en stråle av infallande röntgenstrålar att diffraktera i många specifika riktningar. Genom att mäta vinklarna och intensiteterna för dessa diffrakterade strålar kan en kristallograf producera en tredimensionell bild av tätheten av elektroner i kristallen. Från denna elektrontäthet kan medelpositionerna för atomerna i kristallen bestämmas, såväl som deras kemiska bindningar , deras kristallografiska störning och diverse annan information.

Eftersom många material kan bilda kristaller - såsom salter , metaller , mineraler , halvledare , såväl som olika oorganiska, organiska och biologiska molekyler - har röntgenkristallografi varit grundläggande i utvecklingen av många vetenskapliga områden. Under de första decennierna av användning bestämde denna metod storleken på atomer, längderna och typerna av kemiska bindningar och skillnaderna i atomskala mellan olika material, särskilt mineraler och legeringar . Metoden avslöjade också strukturen och funktionen hos många biologiska molekyler, inklusive vitaminer , läkemedel, proteiner och nukleinsyror som DNA . Röntgenkristallografi är fortfarande den primära metoden för att karakterisera den atomära strukturen av nya material och i kräsna material som verkar liknande genom andra experiment . Röntgenkristallstrukturer kan också stå för ovanliga elektroniska eller elastiska egenskaper hos ett material, kasta ljus över kemiska interaktioner och processer , eller tjäna som grund för att designa läkemedel mot sjukdomar .

I en enkristallröntgendiffraktionsmätning är en kristall monterad på en goniometer . Goniometern används för att placera kristallen i utvalda riktningar. Kristallen är upplyst med en finfokuserad monokromatisk stråle av röntgenstrålar, som producerar ett diffraktionsmönster av regelbundet åtskilda fläckar som kallas reflektioner . De tvådimensionella bilderna tagna med olika orienteringar omvandlas till en tredimensionell modell av tätheten av elektroner i kristallen med hjälp av den matematiska metoden Fourier-transformationer , kombinerat med kemiska data som är kända för provet. Dålig upplösning (suddighet) eller till och med fel kan uppstå om kristallerna är för små eller inte tillräckligt enhetliga i sin inre makeup.

Röntgenkristallografi är relaterad till flera andra metoder för att bestämma atomära strukturer. Liknande diffraktionsmönster kan produceras genom att sprida elektroner eller neutroner , och neutronspridning kan tolkas på liknande sätt genom Fourier-transformation . Om enkristaller av tillräcklig storlek inte kan erhållas, kan olika andra röntgenmetoder användas för att erhålla mindre detaljerad information; sådana metoder inkluderar fiberdiffraktion , pulverdiffraktion och (om provet inte är kristalliserat) småvinkelröntgenspridning ( SAXS). Om materialet som undersöks endast är tillgängligt i form av nanokristallina pulver eller lider av dålig kristallinitet, kan metoderna för elektrondiffraktion , transmissionselektronmikroskopi och elektronkristallografi användas för att bestämma atomstrukturen.

För alla ovan nämnda röntgendiffraktionsmetoder är spridningen elastisk ; de spridda röntgenstrålarna har samma våglängd som den inkommande röntgenstrålningen. Däremot oelastiska röntgenspridningsmetoder användbara för att studera excitationer av provet såsom plasmoner , kristallfälts- och orbitalexcitationer, magnoner och fononer , snarare än fördelningen av dess atomer.

Historia

Tidig vetenskaplig historia av kristaller och röntgenstrålar

Ritning av kvadratisk (A) och sexkantig (B) packning från Keplers verk, Strena seu de Nive Sexangula .

Den hexagonala symmetrin hos snöflingor är resultatet av det tetraedriska arrangemanget av vätebindningar runt varje vattenmolekyl.

Kristaller, även om de länge beundrades för sin regelbundenhet och symmetri, undersöktes inte vetenskapligt förrän på 1600-talet. Johannes Kepler antog i sitt verk Strena seu de Nive Sexangula (A New Year's Gift of Hexagonal Snow) (1611) att den hexagonala symmetrin hos snöflingakristaller berodde på en regelbunden packning av sfäriska vattenpartiklar. Den danske vetenskapsmannen Nicolas Steno (1669) var banbrytande för experimentella undersökningar av kristallsymmetri. Steno visade att vinklarna mellan ytorna är desamma i varje exemplar av en viss typ av kristall. René Just Haüy (1784) upptäckte att varje yta av en kristall kan beskrivas genom enkla staplingsmönster av block av samma form och storlek. Därför kunde William Hallowes Miller 1839 ge varje ansikte en unik etikett med tre små heltal, Miller-indexen som fortfarande används för att identifiera kristallytor. Haüys studie ledde till idén att kristaller är en regelbunden tredimensionell grupp (ett Bravais-gitter ) av atomer och molekyler ; en enda enhetscell upprepas i det oändliga längs tre huvudriktningar. På 1800-talet utarbetades en komplett katalog över de möjliga symmetrierna hos en kristall av Johan Hessel , Auguste Bravais , Evgraf Fedorov , Arthur Schönflies och (försenat) William Barlow (1894). Barlow föreslog flera kristallstrukturer på 1880-talet som validerades senare genom röntgenkristallografi; dock var tillgängliga data för knappa på 1880-talet för att acceptera hans modeller som avgörande.

Modell av arrangemanget av vattenmolekyler i is, avslöjar vätebindningarna (1) som håller ihop det fasta ämnet.

Wilhelm Röntgen upptäckte röntgenstrålning 1895. Fysiker var osäkra på röntgenstrålningens natur, men misstänkte snart att de var vågor av elektromagnetisk strålning . Maxwell -teorin om elektromagnetisk strålning var väl accepterad, och experiment av Charles Glover Barkla visade att röntgenstrålar uppvisade fenomen associerade med elektromagnetiska vågor, inklusive transversell polarisation och spektrallinjer liknande de som observerades i de synliga våglängderna. Barkla skapade också röntgennotationen, och noterade 1909 två separata typer av diffraktionsstrålar, först genom att namnge dem "A" och "B" och sedan anta att det kan finnas linjer före "A", startade han en alfabetisk numrering som börjar med "K". Enkelslitsexperiment i Arnold Sommerfelds laboratorium antydde att röntgenstrålar hade en våglängd på cirka 1 ångström . Röntgenstrålar är inte bara vågor utan är också fotoner och har partikelegenskaper som får Sommerfeld att mynta namnet Bremsstrahlung för denna vågliknande typ av diffraktion. Albert Einstein introducerade fotonkonceptet 1905, men det blev inte allmänt accepterat förrän 1922, när Arthur Compton bekräftade det genom spridning av röntgenstrålar från elektroner. Röntgenstrålningens partikelliknande egenskaper, såsom deras jonisering av gaser, hade fått William Henry Bragg att 1907 hävda att röntgenstrålar inte var elektromagnetisk strålning. Braggs åsikt visade sig vara impopulär och observationen av röntgendiffraktion av Max von Laue 1912 bekräftade för de flesta forskare att röntgenstrålning är en form av elektromagnetisk strålning.

Röntgendiffraktion

Den inkommande strålen (som kommer från övre vänster) får varje spridare att återutstråla en liten del av sin intensitet som en sfärisk våg. Om spridare är arrangerade symmetriskt med en separation d , kommer dessa sfäriska vågor att vara synkroniserade (lägga till konstruktivt) endast i riktningar där deras väglängdsskillnad 2 d sin θ är lika med en heltalsmultipel av våglängden λ. I det fallet avböjes en del av den inkommande strålen med en vinkel 2θ, vilket ger en reflektionsfläck i diffraktionsmönstret .

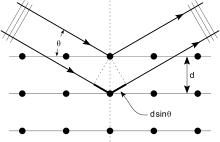
Kristaller är regelbundna uppsättningar av atomer, och röntgenstrålar kan betraktas som vågor av elektromagnetisk strålning. Atomer sprider röntgenvågor, främst genom atomernas elektroner. Precis som en havsvåg som träffar en fyr producerar sekundära cirkulära vågor som emanerar från fyren, så producerar en röntgenstråle som träffar en elektron sekundära sfäriska vågor som utgår från elektronen. Detta fenomen är känt som elastisk spridning , och elektronen (eller fyren) är känd som spridaren . En regelbunden uppsättning av spridare producerar en regelbunden uppsättning av sfäriska vågor. Även om dessa vågor tar ut varandra i de flesta riktningar genom destruktiv interferens , lägger de till konstruktivt i några specifika riktningar, bestämt av Braggs lag :

$n\lambda =2d\sin \theta$

Här är d avståndet mellan diffraktionsplan, $\theta$ är infallsvinkeln, n är vilket heltal som helst och λ är strålens våglängd. Dessa specifika riktningar visas som fläckar på diffraktionsmönstret som kallas reflektioner . Således är röntgendiffraktion ett resultat av en elektromagnetisk våg (röntgenstrålningen) som träffar en regelbunden uppsättning av spridare (det upprepade arrangemanget av atomer i kristallen).

Röntgenstrålar används för att producera diffraktionsmönstret eftersom deras våglängd λ vanligtvis är i samma storleksordning (1–100 ångström) som avståndet d mellan planen i kristallen. I princip producerar alla vågor som träffar en regelbunden uppsättning av spridare diffraktion , som förutspåddes först av Francesco Maria Grimaldi 1665. För att producera signifikant diffraktion bör avståndet mellan spridarna och våglängden på den träffande vågen vara lika i storlek. Som illustration rapporterades diffraktionen av solljus genom en fågels fjäder först av James Gregory under det senare 1600-talet. De första artificiella diffraktionsgittren för synligt ljus konstruerades av David Rittenhouse 1787 och Joseph von Fraunhofer 1821. Synligt ljus har dock en för lång våglängd (vanligtvis 5500 ångström) för att observera diffraktion från kristaller. Före de första röntgendiffraktionsexperimenten var avstånden mellan gitterplanen i en kristall inte kända med säkerhet.

Tanken att kristaller skulle kunna användas som ett diffraktionsgitter för röntgenstrålar uppstod 1912 i ett samtal mellan Paul Peter Ewald och Max von Laue i den engelska trädgården i München . Ewald hade föreslagit en resonatormodell av kristaller för sin avhandling, men denna modell kunde inte valideras med hjälp av synligt ljus , eftersom våglängden var mycket större än avståndet mellan resonatorerna. Von Laue insåg att elektromagnetisk strålning med en kortare våglängd behövdes för att observera så små avstånd, och föreslog att röntgenstrålar kan ha en våglängd som är jämförbar med enhetscellsavståndet i kristaller. Von Laue arbetade med två tekniker, Walter Friedrich och hans assistent Paul Knipping, för att lysa en stråle av röntgenstrålar genom en kopparsulfatkristall och registrera dess diffraktion på en fotografisk platta . Efter att ha utvecklats visade plattan ett stort antal väldefinierade fläckar arrangerade i ett mönster av korsande cirklar runt fläcken som produceras av den centrala strålen. Von Laue utvecklade en lag som kopplar samman spridningsvinklarna och storleken och orienteringen av enhetscellsavstånden i kristallen, för vilken han tilldelades Nobelpriset i fysik 1914.

Spridning

Som beskrivs i den matematiska härledningen nedan bestäms röntgenspridningen av tätheten av elektroner i kristallen. Eftersom energin hos en röntgenstrålning är mycket större än en valenselektron, kan spridningen modelleras som Thomson-spridning , interaktionen mellan en elektromagnetisk stråle och en fri elektron. Denna modell används generellt för att beskriva polariseringen av den spridda strålningen.

Intensiteten av Thomson-spridning för en partikel med massa m och elementär laddning q är:

$I_{o}=I_ {e}\left({\frac {q^{4}}{m^{2}c^{4}}}\right){\frac {1+\cos ^{2}2\theta }{2 }}=I_{e}7.94.10^{-26}{\frac {1+\cos ^{2}2\theta }{2}}=I_{e}f$

Därför bidrar atomkärnorna, som är mycket tyngre än en elektron, försumbart till den spridda röntgenstrålningen. Följaktligen kan den koherenta spridningen som detekteras från en atom noggrant approximeras genom att analysera den kollektiva spridningen från elektronerna i systemet.

Utveckling från 1912 till 1920

Även om diamanter (överst till vänster) och grafit (överst till höger) är identiska i kemisk sammansättning - eftersom de båda är rent kol - visade röntgenkristallografi att arrangemanget av deras atomer (nederst) förklarar deras olika egenskaper. I diamant är kolatomerna arrangerade tetraedriskt och hålls samman av enkla kovalenta bindningar , vilket gör den stark i alla riktningar. Däremot är grafit sammansatt av staplade ark. Inom arket är bindningen kovalent och har hexagonal symmetri, men det finns inga kovalenta bindningar mellan arken, vilket gör grafit lätt att klyva till flingor.

Efter Von Laues banbrytande forskning utvecklades området snabbt, framför allt av fysikerna William Lawrence Bragg och hans far William Henry Bragg . 1912–1913 utvecklade den yngre Bragg Braggs lag , som förbinder den observerade spridningen med reflektioner från jämnt fördelade plan inom kristallen. Braggs, far och son, delade 1915 års Nobelpris i fysik för sitt arbete med kristallografi. De tidigaste strukturerna var i allmänhet enkla och markerade av endimensionell symmetri. Men eftersom beräkningsmetoder och experimentella metoder förbättrades under de kommande decennierna, blev det möjligt att härleda tillförlitliga atompositioner för mer komplicerade två- och tredimensionella arrangemang av atomer i enhetscellen.

Potentialen hos röntgenkristallografi för att bestämma strukturen hos molekyler och mineraler - då endast vagt känt från kemiska och hydrodynamiska experiment - realiserades omedelbart. De tidigaste strukturerna var enkla oorganiska kristaller och mineraler, men även dessa avslöjade grundläggande fysik- och kemilagar. Den första atomupplösningsstrukturen som "löstes" (dvs. bestämdes) 1914 var den av bordssalt . Fördelningen av elektroner i bordsaltstrukturen visade att kristaller inte nödvändigtvis består av kovalent bundna molekyler, och bevisade förekomsten av joniska föreningar . Strukturen av diamant löstes samma år, vilket bevisade det tetraedriska arrangemanget av dess kemiska bindningar och visade att längden på C-C enkelbindning var 1,52 ångström. Andra tidiga strukturer inkluderade koppar , kalciumfluorid (CaF ₂ , även känd som fluorit ), kalcit (CaCO ₃ ) och pyrit (FeS ₂ ) 1914; spinell (MgAl ₂ O ₄ ) 1915; rutil- och anatasformerna av titandioxid (TiO ₂ ) 1916; pyrokroit Mn(OH) ₂ och, i förlängningen, brucite Mg(OH) ₂ 1919. Också 1919 bestämdes natriumnitrat ( NaNO ₃ ) och cesiumdiklorjodid (CsICl _{2 ) av} Ralph Walter Graystone Wyckoff och hexagonwurtzite ZnS)-strukturen blev känd 1920.

Grafitens struktur löstes 1916 med den relaterade metoden för pulverdiffraktion , som utvecklades av Peter Debye och Paul Scherrer och oberoende av Albert Hull 1917. Grafitens struktur bestämdes från enkristalldiffraktion 1924 av två grupper självständigt. Hull använde också pulvermetoden för att bestämma strukturerna hos olika metaller, som järn och magnesium.

Kulturell och estetisk betydelse

År 1951 var Festival Pattern Group vid Festival of Britain värd för en samarbetsgrupp av textiltillverkare och erfarna kristallografer för att designa spetsar och tryck baserat på röntgenkristallografi av insulin , porslin och hemoglobin . En av de ledande forskarna i projektet var Helen Megaw , assisterande forskningsdirektör vid Cavendish Laboratory i Cambridge vid den tiden. Megaw är krediterad som en av de centrala figurerna som hämtade inspiration från kristalldiagram och såg sin potential i design. 2008 kurerade Wellcome Collection i London en utställning om Festival Pattern Group kallad "From Atom to Patterns".

Bidrag till kemi och materialvetenskap

Röntgenkristallografi har lett till en bättre förståelse av kemiska bindningar och icke-kovalenta interaktioner . De första studierna avslöjade atomernas typiska radier och bekräftade många teoretiska modeller för kemisk bindning, såsom den tetraedriska bindningen av kol i diamantstrukturen, den oktaedriska bindningen av metaller som observerats i ammoniumhexaklorplatinat (IV) och den resonans som observeras i plan karbonatgrupp och i aromatiska molekyler. Kathleen Lonsdales struktur från 1928 av hexametylbensen etablerade den hexagonala symmetrin av bensen och visade en tydlig skillnad i bindningslängd mellan de alifatiska C–C-bindningarna och aromatiska C–C-bindningarna; detta fynd ledde till idén om resonans mellan kemiska bindningar, vilket fick djupgående konsekvenser för kemins utveckling. Hennes slutsatser förutsågs av William Henry Bragg , som publicerade modeller av naftalen och antracen 1921 baserade på andra molekyler, en tidig form av molekylär ersättning .

Även på 1920-talet utvecklade Victor Moritz Goldschmidt och senare Linus Pauling regler för att eliminera kemiskt osannolika strukturer och för att bestämma atomernas relativa storlekar. Dessa regler ledde till strukturen av brookite (1928) och en förståelse för den relativa stabiliteten hos rutil- , brookit- och anatasformerna av titandioxid .

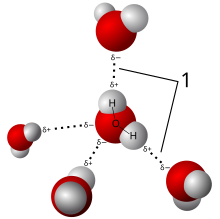
Avståndet mellan två bundna atomer är ett känsligt mått på bindningsstyrkan och dess bindningsordning ; sålunda har röntgenkristallografiska studier lett till upptäckten av ännu mer exotiska typer av bindning inom oorganisk kemi , såsom metall-metall-dubbelbindningar, metall-metall-fyrdubbelbindningar och tre-center, två-elektronbindningar. Röntgenkristallografi - eller, strikt taget, ett oelastiskt Compton-spridningsexperiment - har också gett bevis för den delvis kovalenta karaktären hos vätebindningar . Inom fältet av metallorganisk kemi initierade röntgenstrukturen av ferrocene vetenskapliga studier av sandwichföreningar , medan Zeises salt stimulerade forskning om "back bonding" och metall-pi-komplex. Slutligen hade röntgenkristallografi en banbrytande roll i utvecklingen av supramolekylär kemi , särskilt för att klargöra strukturerna för kronetrarna och principerna för värd-gästkemi .

Röntgendiffraktion är ett mycket kraftfullt verktyg vid katalysatorutveckling . Ex-situ mätningar utförs rutinmässigt för att kontrollera kristallstrukturen hos material eller för att nysta upp nya strukturer. In-situ-experiment ger en omfattande förståelse om katalysatorers strukturella stabilitet under reaktionsförhållanden.

Inom materialvetenskap har många komplicerade oorganiska och metallorganiska system analyserats med enkristallmetoder, såsom fullerener , metalloporfyriner och andra komplicerade föreningar. Enkristalldiffraktion används också inom läkemedelsindustrin , på grund av nyligen problem med polymorfer . De viktigaste faktorerna som påverkar kvaliteten på enkristallstrukturer är kristallens storlek och regelbundenhet; omkristallisation är en vanlig teknik för att förbättra dessa faktorer i småmolekylära kristaller. Cambridge Structural Database innehåller över 1 000 000 strukturer från och med juni 2019; över 99% av dessa strukturer bestämdes genom röntgendiffraktion.

Mineralogi och metallurgi

Första röntgendiffraktionsvy av Mars-jord – CheMin-analys avslöjar fältspat , pyroxener , olivin och mer ( Curiosity rover på " Rocknest ", 17 oktober 2012).

Sedan 1920-talet har röntgendiffraktion varit den huvudsakliga metoden för att bestämma arrangemanget av atomer i mineraler och metaller . Tillämpningen av röntgenkristallografi på mineralogi började med strukturen av granat , som bestämdes 1924 av Menzer. En systematisk röntgenkristallografisk studie av silikaterna genomfördes på 1920-talet. Denna studie visade att när Si / O -förhållandet ändras, uppvisar silikatkristallerna betydande förändringar i sina atomära arrangemang. Machatschki utökade dessa insikter till mineraler där aluminium ersätter silikonatomerna i silikaterna. Den första tillämpningen av röntgenkristallografi på metallurgi inträffade också i mitten av 1920-talet. Mest anmärkningsvärt Linus Paulings struktur av legeringen Mg ₂ Sn till hans teori om stabiliteten och strukturen hos komplexa jonkristaller.

Den 17 oktober 2012 utförde Curiosity-rovern på planeten Mars vid " Rocknest " den första röntgendiffraktionsanalysen av Mars mark . Resultaten från roverns CheMin-analysator avslöjade närvaron av flera mineraler, inklusive fältspat , pyroxener och olivin , och antydde att marsjorden i provet liknade den "vittrade basaltjorden " i Hawaii-vulkaner .

Tidiga organiska och små biologiska molekyler

Den tredimensionella strukturen av penicillin , löst av Dorothy Crowfoot Hodgkin 1945. De gröna, röda, gula och blå sfärerna representerar atomer av kol , syre , svavel och kväve , respektive. De vita sfärerna representerar väte , som bestämdes matematiskt snarare än genom röntgenanalys.

Den första strukturen av en organisk förening, hexametylentetramin , löstes 1923. Detta följdes av flera studier av långkedjiga fettsyror , som är en viktig komponent i biologiska membran . På 1930-talet började strukturerna för mycket större molekyler med tvådimensionell komplexitet att lösas. Ett betydande framsteg var strukturen av phthalocyanine , en stor plan molekyl som är nära besläktad med porfyrinmolekyler som är viktiga i biologi, såsom heme , corrin och klorofyll .

Röntgenkristallografi av biologiska molekyler tog fart med Dorothy Crowfoot Hodgkin , som löste strukturerna för kolesterol (1937), penicillin (1946) och vitamin B ₁₂ (1956), för vilka hon belönades med Nobelpriset i kemi 1964. I 1969 lyckades hon lösa insulinstrukturen, som hon arbetade med i över trettio år.

Biologisk makromolekylär kristallografi

Banddiagram över strukturen av myoglobin , som visar alfaspiraler . Sådana proteiner är långa, linjära molekyler med tusentals atomer; ändå har den relativa positionen för varje atom bestämts med subatomär upplösning genom röntgenkristallografi. Eftersom det är svårt att visualisera alla atomer på en gång visar bandet den grova vägen för proteinets ryggrad från dess N-terminal till dess C-terminal.

- talet, med början med strukturen av kaskelotmyoglobin av Sir John Cowdery Kendrew , för vilket han delade Nobelpriset i kemi med Max Perutz 1962. Sedan framgången har över 130 000 röntgenkristallstrukturer av proteiner, nukleinsyror och andra biologiska molekyler fastställts. Den närmast konkurrerande metoden i antal analyserade strukturer är kärnmagnetisk resonans (NMR) spektroskopi, som har löst mindre än en tiondel så många. Kristallografi kan lösa strukturer av godtyckligt stora molekyler, medan NMR i lösningstillstånd är begränsad till relativt små (mindre än 70 kDa ) . Röntgenkristallografi används rutinmässigt för att bestämma hur ett farmaceutiskt läkemedel interagerar med dess proteinmål och vilka förändringar som kan förbättra det. Emellertid förblir inre membranproteiner utmanande att kristallisera eftersom de kräver detergenter eller andra denatureringsmedel för att solubilisera dem i isolering, och sådana detergenter stör ofta kristallisering. Membranproteiner är en stor komponent i genomet och inkluderar många proteiner av stor fysiologisk betydelse, såsom jonkanaler och receptorer . Heliumkryogenik används för att förhindra strålningsskador i proteinkristaller.

I andra änden av storleksskalan kan även relativt små molekyler utgöra utmaningar för upplösningsförmågan hos röntgenkristallografi. Strukturen som tilldelades 1991 till antibiotikumet isolerat från en marin organism, diazonamid A (C ₄₀ H ₃₄ Cl ₂ N ₆ O ₆ , molmassa 765,65 g/mol), visade sig vara felaktig genom det klassiska beviset på struktur: ett syntetiskt prov var inte identisk med naturprodukten. Misstaget tillskrevs oförmågan hos röntgenkristallografi att skilja mellan den korrekta -OH / -NH och de utbytta -NH ₂ / -O- grupperna i den felaktiga strukturen. Med framsteg inom instrumentering kan emellertid liknande grupper särskiljas med hjälp av moderna enkristallröntgendiffraktometrar.

Trots att det är ett ovärderligt verktyg inom strukturell biologi , har proteinkristallografi några inneboende problem i sin metodik som hindrar datatolkning. Kristallgittret, som bildas under kristallisationsprocessen, innehåller många enheter av det renade proteinet, som är tätt och symmetriskt packade i kristallen. När man letar efter ett tidigare okänt protein kan det vara svårt att ta reda på dess form och gränser inom kristallgittret. Proteiner är vanligtvis sammansatta av mindre underenheter, och uppgiften att skilja mellan underenheterna och identifiera det faktiska proteinet kan vara utmanande även för de erfarna kristallograferna. De icke-biologiska gränssnitten som uppstår under kristallisering är kända som kristallpackningskontakter (eller helt enkelt kristallkontakter) och kan inte särskiljas med kristallografiska medel. När en ny proteinstruktur löses genom röntgenkristallografi och deponeras i Protein Data Bank , uppmanas dess författare att specificera den "biologiska sammansättningen" som skulle utgöra det funktionella, biologiskt relevanta proteinet. Fel, saknade data och felaktiga anteckningar under inlämnandet av data ger dock upphov till oklara strukturer och äventyrar databasens tillförlitlighet. Felfrekvensen enbart i fallet med felaktiga anteckningar har rapporterats vara uppåt 6,6 % eller ungefär 15 %, utan tvekan en icke-trivial storlek med tanke på antalet deponerade strukturer. Detta "gränssnittsklassificeringsproblem" angrips vanligtvis av beräkningsmetoder och har blivit ett erkänt ämne inom strukturell bioinformatik .

Spridningstekniker

Ytterligare information: Röntgenspridningstekniker

Elastisk vs oelastisk spridning

Röntgenkristallografi är en form av elastisk spridning ; de utgående röntgenstrålarna har samma energi, och därmed samma våglängd, som de inkommande röntgenstrålarna, endast med ändrad riktning. Däremot oelastisk spridning när energi överförs från den inkommande röntgenstrålen till kristallen, t.ex. genom att excitera en elektron i det inre skalet till en högre energinivå . Sådan oelastisk spridning minskar energin (eller ökar våglängden) hos den utgående strålen. Oelastisk spridning är användbar för att undersöka sådana excitationer av materia, men inte för att bestämma fördelningen av spridare inom materien, vilket är målet med röntgenkristallografi.

Röntgenstrålar varierar i våglängd från 10 till 0,01 nanometer ; en typisk våglängd som används för kristallografi är 1 Å (0,1 nm), vilket är på skalan av kovalenta kemiska bindningar och radien för en enda atom. Längre våglängdsfotoner (som ultraviolett strålning ) skulle inte ha tillräcklig upplösning för att bestämma atompositionerna. I den andra ytterligheten är fotoner med kortare våglängd, såsom gammastrålar, svåra att producera i stort antal, svåra att fokusera och interagerar för starkt med materia, vilket ger partikel-antipartikelpar . Därför är röntgenstrålar "sweetspot" för våglängd när man bestämmer atomupplösningsstrukturer från spridningen av elektromagnetisk strålning .

Andra röntgentekniker

Andra former av elastisk röntgenspridning förutom enkristalldiffraktion inkluderar pulverdiffraktion , Small-Angle X-ray Scatering ( SAXS ) och flera typer av röntgenfiberdiffraktion, som användes av Rosalind Franklin för att bestämma dubbelhelixstrukturen av DNA . I allmänhet erbjuder enkristallröntgendiffraktion mer strukturell information än dessa andra tekniker; det kräver dock en tillräckligt stor och regelbunden kristall, vilket inte alltid är tillgängligt.

Dessa spridningsmetoder använder i allmänhet monokromatiska röntgenstrålar, som är begränsade till en enda våglängd med mindre avvikelser. Ett brett spektrum av röntgenstrålar (det vill säga en blandning av röntgenstrålar med olika våglängder) kan också användas för att utföra röntgendiffraktion, en teknik som kallas Laue-metoden. Detta är metoden som användes i den ursprungliga upptäckten av röntgendiffraktion. Laue-spridning ger mycket strukturell information med endast en kort exponering för röntgenstrålen, och används därför i strukturella studier av mycket snabba händelser ( Time resolved crystallography) . Den är dock inte lika väl lämpad som monokromatisk spridning för att bestämma hela atomstrukturen hos en kristall och fungerar därför bättre med kristaller med relativt enkla atomarrangemang.

Laue-backreflektionsläget registrerar röntgenstrålar som sprids bakåt från en bredspektrumkälla. Detta är användbart om provet är för tjockt för att röntgenstrålar ska kunna överföras genom det. Diffraktionsplanen i kristallen bestäms genom att veta att normalen till diffraktionsplanet delar vinkeln mellan den infallande strålen och den diffrakterade strålen. Ett Greninger-diagram kan användas för att tolka Laue-fotografiet med bakreflektion.

Elektron- och neutrondiffraktion

Andra partiklar, såsom elektroner och neutroner , kan användas för att producera ett diffraktionsmönster . Även om elektron-, neutron- och röntgenspridning är baserad på olika fysikaliska processer, analyseras de resulterande diffraktionsmönstren med samma diffraktionstekniker .

Såsom härleds nedan är elektrondensiteten inom kristall- och diffraktionsmönstren ofta relaterad till en enkel matematisk metod, Fouriertransformen, som gör att densiteten kan beräknas relativt enkelt från mönstren. Detta fungerar dock endast om spridningen är svag , dvs om de spridda strålarna är mycket mindre intensiva än den inkommande strålen. Svagt spridda röntgen- eller neutronstrålar passerar genom resten av kristallen utan att genomgå en andra spridningshändelse. Sådana återspridda vågor kallas "sekundär spridning" eller "dynamisk diffraktion" och ändrar analysen. Alla tillräckligt tjocka kristaller kommer att producera dynamisk diffraktion, men eftersom röntgenstrålar och neutroner interagerar relativt svagt med materia, är detta i allmänhet inte ett betydande problem när de används.

Eftersom de interagerar via Coulomb-krafterna är spridningen av elektroner genom materia 1000 eller fler gånger starkare än för röntgenstrålar. Därför producerar elektronstrålar stark dynamisk spridning även för relativt tunna kristaller (>10 nm). Även om det finns likheter mellan diffraktionen av röntgenstrålar och elektroner, som kan hittas i boken av John M. Cowley , är tillvägagångssättet vanligtvis annorlunda eftersom det är baserat på Hans Bethes ursprungliga tillvägagångssätt och lösning av Schrödinger-ekvationen för relativistiska elektroner , snarare än ett kinematiskt eller Braggs lag tillvägagångssätt. Information om mycket små regioner, ner till enstaka atomer är möjlig. Användningsområdet för elektrondiffraktion , transmissionselektronmikroskopi och transmissionselektronkristallografi med högenergielektroner är omfattande; se relevanta länkar för mer information och citat. Förutom transmissionsmetoder lågenergielektrondiffraktion en teknik där elektroner är tillbakaspridda på ytor och har använts i stor utsträckning för att bestämma ytstrukturer på atomär skala, och reflektion med hög energi elektrondiffraktion är en annan som används i stor utsträckning för att övervaka tillväxt av tunn film.

Neutrondiffraktion är en utmärkt metod för strukturbestämning, även om det har varit svårt att få fram intensiva, monokromatiska strålar av neutroner i tillräckliga mängder. Traditionellt kärnreaktorer använts, även om källor som producerar neutroner genom spallation blir alltmer tillgängliga. Eftersom neutronerna är oladdade sprids de mycket lättare från atomkärnorna snarare än från elektronerna. Därför är neutronspridning mycket användbar för att observera positionerna för lätta atomer med få elektroner, särskilt väte , som är väsentligen osynligt i röntgendiffraktionen. Neutronspridning har också den anmärkningsvärda egenskapen att lösningsmedlet kan göras osynligt genom att justera förhållandet mellan normalt vatten , H ₂ O, och tungt vatten , D ₂ O.

Metoder

Översikt över enkristallröntgendiffraktion

Arbetsflöde för att lösa strukturen hos en molekyl genom röntgenkristallografi.

Den äldsta och mest exakta metoden för röntgenkristallografi är enkristallröntgendiffraktion, där en stråle av röntgenstrålar träffar en enda kristall och producerar spridda strålar . När de landar på ett stycke film eller annan detektor bildar dessa strålar ett diffraktionsmönster av fläckar; styrkorna och vinklarna för dessa strålar registreras när kristallen gradvis roteras. Varje fläck kallas en reflektion , eftersom den motsvarar reflektionen av röntgenstrålar från en uppsättning jämnt fördelade plan inom kristallen. För enkristaller med tillräcklig renhet och regelbundenhet kan röntgendiffraktionsdata bestämma de genomsnittliga kemiska bindningarnas längder och vinklar inom några tusendels ångström respektive inom några tiondelar av en grad . Atomerna i en kristall är inte statiska, utan oscillerar runt sina medelpositioner, vanligtvis med mindre än några tiondels ångström. Röntgenkristallografi gör det möjligt att mäta storleken på dessa svängningar.

Procedur

Tekniken för enkristallröntgenkristallografi har tre grundläggande steg. Det första – och ofta svåraste – steget är att få en adekvat kristall av det material som studeras. Kristallen bör vara tillräckligt stor (vanligtvis större än 0,1 mm i alla dimensioner), ren till sammansättning och regelbunden struktur, utan betydande inre defekter som sprickor eller tvillingar .

I det andra steget placeras kristallen i en intensiv stråle av röntgenstrålar, vanligtvis med en enda våglängd ( monokroma röntgenstrålar ), som producerar det regelbundna mönstret av reflektioner. Vinklarna och intensiteterna för diffrakterade röntgenstrålar mäts, där varje förening har ett unikt diffraktionsmönster. När kristallen gradvis roteras försvinner tidigare reflektioner och nya dyker upp; intensiteten av varje fläck registreras vid varje orientering av kristallen. Flera datamängder kan behöva samlas in, där varje uppsättning täcker något mer än en halv hel rotation av kristallen och innehåller vanligtvis tiotusentals reflektioner.

I det tredje steget kombineras dessa data beräkningsmässigt med kompletterande kemisk information för att producera och förfina en modell av arrangemanget av atomer i kristallen. Den slutliga, förfinade modellen av atomarrangemanget – som nu kallas en kristallstruktur – lagras vanligtvis i en offentlig databas.

Begränsningar

Se även: Upplösning (elektrondensitet)

När kristallens repeterande enhet, dess enhetscell, blir större och mer komplex, blir bilden på atomnivå som tillhandahålls av röntgenkristallografi mindre välupplöst (mer "suddrig") för ett givet antal observerade reflektioner. Två begränsande fall av röntgenkristallografi - "liten molekyl" (som inkluderar kontinuerliga oorganiska fasta ämnen) och "makromolekylär" kristallografi - urskiljs ofta. Småmolekylär kristallografi involverar typiskt kristaller med färre än 100 atomer i sin asymmetriska enhet ; sådana kristallstrukturer är vanligtvis så väl upplösta att atomerna kan urskiljas som isolerade "blobbar" av elektrondensitet. Däremot makromolekylär kristallografi ofta tiotusentals atomer i enhetscellen. Sådana kristallstrukturer är i allmänhet mindre välupplösta (mer "utsmetade"); atomerna och de kemiska bindningarna framstår som rör med elektrondensitet, snarare än som isolerade atomer. I allmänhet är små molekyler också lättare att kristallisera än makromolekyler; dock har röntgenkristallografi visat sig möjlig även för virus och proteiner med hundratusentals atomer, genom förbättrad kristallografisk avbildning och teknologi. Även om röntgenkristallografi normalt endast kan utföras om provet är i kristallform, har ny forskning gjorts för att ta prover från icke-kristallina former av prover.

Kristallisation

Ytterligare information: Kristallisation , Omkristallisation (kemi) § Enkla perfekta kristaller (för röntgenanalys) och Proteinkristallisation

En proteinkristall sedd under ett mikroskop . Kristaller som används i röntgenkristallografi kan vara mindre än en millimeter tvärs över.

Även om kristallografi kan användas för att karakterisera störningen i en oren eller oregelbunden kristall, kräver kristallografi i allmänhet en ren kristall med hög regelbundenhet för att lösa strukturen hos ett komplicerat arrangemang av atomer. Rena, vanliga kristaller kan ibland erhållas från naturliga eller syntetiska material, såsom prover av metaller , mineraler eller andra makroskopiska material. Regelbundenheten hos sådana kristaller kan ibland förbättras med makromolekylär kristallglödgning och andra metoder. Men i många fall är att erhålla en kristall av diffraktionskvalitet den främsta barriären för att lösa dess atomupplösningsstruktur.

Småmolekylär och makromolekylär kristallografi skiljer sig åt i intervallet av möjliga tekniker som används för att producera kristaller av diffraktionskvalitet. Små molekyler har i allmänhet få grader av konformationsfrihet och kan kristalliseras med ett brett spektrum av metoder, såsom kemisk ångavsättning och omkristallisation . Däremot har makromolekyler i allmänhet många frihetsgrader och deras kristallisering måste utföras för att bibehålla en stabil struktur. Till exempel kan proteiner och större RNA- molekyler inte kristalliseras om deras tertiära struktur har vecklats ut ; därför är området för kristallisationsbetingelser begränsad till lösningsbetingelser där sådana molekyler förblir vikta.

Tre metoder för att förbereda kristaller, A: Hängande droppe. B: Sittdropp. C: Mikrodialys

Proteinkristaller odlas nästan alltid i lösning. Det vanligaste tillvägagångssättet är att sänka lösligheten av dess komponentmolekyler mycket gradvis; om detta görs för snabbt kommer molekylerna att falla ut från lösningen och bilda ett värdelöst damm eller amorf gel på botten av behållaren. Kristalltillväxt i lösning kännetecknas av två steg: kärnbildning av en mikroskopisk kristallit (möjligen med endast 100 molekyler), följt av tillväxt av den kristalliten, idealiskt till en kristall av diffraktionskvalitet. Lösningsbetingelserna som gynnar det första steget (kärnbildning) är inte alltid samma förhållanden som gynnar det andra steget (efterföljande tillväxt). Kristallografens mål är att identifiera lösningsförhållanden som gynnar utvecklingen av en enda, stor kristall, eftersom större kristaller ger förbättrad upplösning av molekylen. Följaktligen bör lösningsbetingelserna missgynna det första steget (kärnbildning) men gynna det andra (tillväxt), så att endast en stor kristall bildas per droppe. Om kärnbildning gynnas för mycket, kommer en dusch av små kristalliter att bildas i droppen, snarare än en stor kristall; om den gynnas för lite kommer ingen kristall att bildas överhuvudtaget. Andra tillvägagångssätt innefattar att kristallisera proteiner under olja, där vattenhaltiga proteinlösningar fördelas under flytande olja och vatten avdunstar genom oljeskiktet. Olika oljor har olika avdunstningspermeabilitet, vilket ger förändringar i koncentrationshastigheter från olika percipient/proteinblandningar.

Det är extremt svårt att förutsäga goda förhållanden för kärnbildning eller tillväxt av välordnade kristaller. I praktiken identifieras gynnsamma förhållanden genom screening ; en mycket stor sats av molekylerna framställs och en mängd olika kristallisationslösningar testas. Hundratals, till och med tusentals, lösningsförhållanden prövas i allmänhet innan man hittar den framgångsrika. De olika förhållandena kan använda en eller flera fysikaliska mekanismer för att sänka molekylens löslighet; till exempel kan vissa ändra pH, vissa innehåller salter av Hofmeister-serien eller kemikalier som sänker lösningens dielektriska konstant, och ytterligare andra innehåller stora polymerer som polyetylenglykol som driver molekylen ur lösningen genom entropiska effekter. Det är också vanligt att prova flera temperaturer för att uppmuntra kristallisation, eller att gradvis sänka temperaturen så att lösningen blir övermättad. Dessa metoder kräver stora mängder av målmolekylen, eftersom de använder hög koncentration av molekylen/molekylerna som ska kristalliseras. På grund av svårigheten att erhålla så stora mängder ( milligram ) protein av kristallisationsgrad, har robotar utvecklats som är kapabla att exakt dispensera kristallisationsförsöksdroppar som är i storleksordningen 100 nanoliter i volym. Detta innebär att 10 gånger mindre protein används per experiment jämfört med kristallisationsförsök som görs för hand (i storleksordningen 1 mikroliter ).

Flera faktorer är kända för att hämma eller fördärva kristallisation. De växande kristallerna hålls i allmänhet vid en konstant temperatur och skyddas från stötar eller vibrationer som kan störa deras kristallisering. Föroreningar i molekylerna eller i kristallisationslösningarna är ofta skadliga mot kristallisation. Konformationell flexibilitet i molekylen tenderar också att göra kristallisering mindre sannolik, på grund av entropi. Molekyler som tenderar att självmontera till vanliga spiraler är ofta ovilliga att montera ihop till kristaller. Kristaller kan fördärvas av tvillingar , vilket kan inträffa när en enhetscell kan packas lika fördelaktigt i flera orienteringar; även om de senaste framstegen inom beräkningsmetoder kan göra det möjligt att lösa strukturen hos vissa tvillingkristaller. Efter att ha misslyckats med att kristallisera en målmolekyl kan en kristallograf försöka igen med en något modifierad version av molekylen; även små förändringar i molekylära egenskaper kan leda till stora skillnader i kristallisationsbeteende.

Datainsamling

Montering av kristallen

Animation som visar de fem möjliga rörelserna med en kappa-goniometer med fyra cirklar. Rotationerna kring var och en av de fyra vinklarna φ, κ, ω och 2θ lämnar kristallen inom röntgenstrålen, men ändrar kristallorienteringen. Detektorn (röd ruta) kan skjutas närmare eller längre bort från kristallen, vilket gör att data med högre upplösning kan tas (om närmare) eller bättre urskiljning av Bragg-topparna (om längre bort).

Kristallen är monterad för mätningar så att den kan hållas i röntgenstrålen och roteras. Det finns flera metoder för montering. Tidigare laddades kristaller i glaskapillärer med kristallisationslösningen (moderluten ) . Nuförtiden är kristaller av små molekyler vanligtvis fästa med olja eller lim till en glasfiber eller en ögla, som är gjord av nylon eller plast och fäst på en solid stång. Proteinkristaller tas upp av en slinga och snabbfrysas sedan med flytande kväve . Denna frysning minskar strålningsskadorna från röntgenstrålningen, liksom bruset i Bragg-topparna på grund av termisk rörelse (Debye-Waller-effekten). Emellertid spricker obehandlade proteinkristaller ofta om de blir snabbfrysta; därför är de i allmänhet fördränkta i en kryoskyddande lösning innan de fryses. Tyvärr kan denna förblötning i sig göra att kristallen spricker, vilket förstör den för kristallografi. I allmänhet identifieras framgångsrika kryotillstånd genom försök och misstag.

Kapillären eller slingan är monterad på en goniometer , vilket gör att den kan placeras exakt i röntgenstrålen och roteras. Eftersom både kristallen och strålen ofta är mycket små, måste kristallen centreras i strålen med en noggrannhet inom ~25 mikrometer, vilket får hjälp av en kamera fokuserad på kristallen. Den vanligaste typen av goniometer är "kappa goniometer", som erbjuder tre rotationsvinklar: ω-vinkeln, som roterar runt en axel vinkelrät mot strålen; κ-vinkeln, kring en axel vid ~50° mot ω-axeln; och slutligen φ-vinkeln kring slingan/kapilläraxeln. När κ-vinkeln är noll, är ω- och φ-axlarna inriktade. K-rotationen möjliggör bekväm montering av kristallen, eftersom armen i vilken kristallen är monterad kan svängas ut mot kristallografen. Oscillationerna som utförs under datainsamlingen (som nämns nedan) involverar endast ω-axeln. En äldre typ av goniometer är fyrcirklar goniometer, och dess släktingar som sexcirklar goniometer.

Röntgenkällor

Ytterligare information: Diffraktometer , synkrotronljuskälla och frielektronlaser

Roterande anod

Småskalig kristallografi kan göras med en lokal röntgenrörkälla, vanligtvis kopplad till en bildplattadetektor . Dessa har fördelen att de är relativt billiga och lätta att underhålla och möjliggör snabb screening och insamling av prover. Våglängden på ljuset som produceras begränsas dock av tillgången på olika anodmaterial . Vidare begränsas intensiteten av den tillförda effekten och den tillgängliga kylkapaciteten för att undvika smältning av anoden. I sådana system kokas elektroner bort från en katod och accelereras genom en stark elektrisk potential på ~50 kV ; efter att ha nått en hög hastighet kolliderar elektronerna med en metallplatta och avger bremsstrahlung och några starka spektrallinjer som motsvarar exciteringen av metallens inre skalelektroner . Den vanligaste metallen som används är koppar , som lätt kan hållas kall på grund av sin höga värmeledningsförmåga , och som producerar starka K _α- och K _β -linjer. K _β -linjen undertrycks ibland med en tunn (~10 µm) nickelfolie. Den enklaste och billigaste varianten av förseglade röntgenrör har en stationär anod ( Crookes-röret ) och drivs med ~2 kW elektronstråleeffekt. Den dyrare varianten har en källa av roterande anod som körs med ~14 kW e-stråleeffekt.

Röntgenstrålar filtreras vanligtvis (genom användning av röntgenfilter ) till en enda våglängd (gjord monokromatisk) och kollimeras till en enda riktning innan de tillåts träffa kristallen. Filtreringen förenklar inte bara dataanalysen, utan tar också bort strålning som bryter ned kristallen utan att bidra med användbar information. Kollimation görs antingen med en kollimator (i princip ett långt rör) eller med ett smart arrangemang av mjukt böjda speglar. Spegelsystem är att föredra för små kristaller (under 0,3 mm) eller med stora enhetsceller (över 150 Å).

Roterande anoder användes av Joanna (Joka) Maria Vandenberg i de första experimenten som visade kraften hos röntgenstrålar för snabb (i realtidsproduktion) screening av stora InGaAsP -tunnfilmsskivor för kvalitetskontroll av kvantbrunnslasrar .

Mikrofokusrör

En nyare utveckling är mikrofokusröret , som kan leverera minst lika högt strålflöde (efter kollimering) som roterande anodkällor men bara kräver en stråleffekt på några tiotals eller hundratals watt istället för att kräva flera kilowatt.

Synkrotronstrålning

Synkrotronstrålningskällor är några av de ljusaste ljuskällorna på jorden och är några av de mest kraftfulla verktyg som finns tillgängliga för röntgenkristallografer. Röntgenstrålar som genereras i stora maskiner som kallas synkrotroner som accelererar elektriskt laddade partiklar, ofta elektroner, till nästan ljusets hastighet och begränsar dem i en (ungefär) cirkulär slinga med hjälp av magnetfält.

Synkrotroner är i allmänhet nationella anläggningar, var och en med flera dedikerade strållinjer där data samlas in utan avbrott. Synkrotroner designades ursprungligen för användning av högenergifysiker som studerar subatomära partiklar och kosmiska fenomen. Den största komponenten i varje synkrotron är dess elektronlagringsring. Denna ring är faktiskt inte en perfekt cirkel, utan en mångsidig polygon. Vid varje hörn av polygonen, eller sektorn, böjer exakt inriktade magneter elektronströmmen. När elektronernas väg böjs avger de energiskurar i form av röntgenstrålar.

Att använda synkrotronstrålning har ofta specifika krav för röntgenkristallografi. Den intensiva joniserande strålningen kan orsaka strålningsskador på prover, särskilt makromolekylära kristaller. Kryokristallografi skyddar provet från strålningsskador genom att frysa kristallen vid temperaturer för flytande kväve ( ~100 K ). Kryokristallografimetoder tillämpas också på roterande anodkällor för hemmakälla. Synkrotronstrålning har emellertid ofta fördelen av våglängder som kan väljas av användaren, vilket möjliggör anomala spridningsexperiment som maximerar onormal signal. Detta är kritiskt i experiment som enkelvåglängds anomal dispersion (SAD) och multi-wavelength anomalous dispersion (MAD).

Frielektronlaser

Frielektronlasrar har utvecklats för användning i röntgenkristallografi. Dessa är de ljusaste röntgenkällorna som finns tillgängliga för närvarande; med röntgenstrålning som kommer i femtosekundskurar . Källans intensitet är sådan att diffraktionsmönster för atomupplösning kan lösas för kristaller som annars är för små för insamling. Men den intensiva ljuskällan förstör också provet, vilket kräver att flera kristaller skjuts. Eftersom varje kristall är slumpmässigt orienterad i strålen måste hundratusentals individuella diffraktionsbilder samlas in för att få en komplett datamängd. Denna metod, seriell femtosekundkristallografi, har använts för att lösa strukturen för ett antal proteinkristallstrukturer, ibland noterade skillnader med ekvivalenta strukturer insamlade från synkrotronkällor.

Registrerar reflektionerna

Ett röntgendiffraktionsmönster av ett kristalliserat enzym. Mönstret av fläckar ( reflektioner ) och den relativa styrkan för varje fläck ( intensiteter ) kan användas för att bestämma enzymets struktur.

När en kristall är monterad och exponerad för en intensiv stråle av röntgenstrålar, sprider den röntgenstrålarna till ett mönster av fläckar eller reflektioner som kan observeras på en skärm bakom kristallen. Ett liknande mönster kan ses genom att lysa en laserpekare på en CD-skiva . De relativa intensiteterna av dessa fläckar ger informationen för att bestämma arrangemanget av molekyler i kristallen i atomär detalj. Intensiteten av dessa reflektioner kan registreras med fotografisk film , en områdesdetektor (såsom en pixeldetektor ) eller med en laddningskopplad enhet (CCD) bildsensor. Topparna vid små vinklar motsvarar lågupplösta data, medan de vid höga vinklar representerar högupplösta data; således kan en övre gräns för strukturens slutliga upplösning bestämmas från de första bilderna. Vissa mått på diffraktionskvalitet kan bestämmas vid denna punkt, såsom mosaiciteten hos kristallen och dess totala störning, som observerats i toppbredderna. Vissa patologier hos kristallen som skulle göra den olämplig för att lösa strukturen kan också diagnostiseras snabbt vid denna tidpunkt.

En bild av fläckar är otillräcklig för att rekonstruera hela kristallen; den representerar bara en liten del av den fullständiga Fouriertransformen. För att samla in all nödvändig information måste kristallen roteras steg för steg genom 180°, med en bild inspelad vid varje steg; faktiskt, något mer än 180° krävs för att täcka det reciproka utrymmet , på grund av krökningen av Ewald-sfären . Men om kristallen har en högre symmetri kan ett mindre vinkelområde såsom 90° eller 45° registreras. Rotationsaxeln bör ändras minst en gång för att undvika att det uppstår en "död fläck" i det reciproka utrymmet nära rotationsaxeln. Det är vanligt att vagga kristallen något (med 0,5–2°) för att fånga ett bredare område av ömsesidigt utrymme.

Flera datamängder kan vara nödvändiga för vissa fasningsmetoder . Till exempel avvikande spridningsfasning med flera våglängder att spridningen registreras minst tre (och vanligtvis fyra, för redundans) våglängder av den inkommande röntgenstrålningen. En enskild kristall kan försämras för mycket under insamlingen av en datamängd, på grund av strålningsskador; i sådana fall måste datauppsättningar på flera kristaller tas.

Dataanalys

Kristallsymmetri, enhetscell och bildskalning

Ytterligare information: Rymdgruppen

Den registrerade serien av tvådimensionella diffraktionsmönster, som var och en motsvarar en annan kristallorientering, omvandlas till en tredimensionell modell av elektrondensiteten; konverteringen använder den matematiska tekniken för Fourier-transformer, vilket förklaras nedan . Varje fläck motsvarar en annan typ av variation i elektrondensiteten; kristallografen måste bestämma vilken variation som motsvarar vilken punkt ( indexering ), de relativa styrkorna för fläckarna i olika bilder ( sammanslagning och skalning ) och hur variationerna ska kombineras för att ge den totala elektrontätheten ( fasning ).

Databehandlingen börjar med att indexera reflektionerna. Detta innebär att identifiera måtten på enhetscellen och vilken bildtopp som motsvarar vilken position i det reciproka rummet. En biprodukt av indexering är att bestämma kristallens symmetri, dvs dess rymdgrupp . Vissa rymdgrupper kan elimineras från början. Till exempel kan reflektionssymmetrier inte observeras i kirala molekyler; sålunda tillåts endast 65 rymdgrupper om 230 möjliga för proteinmolekyler som nästan alltid är kirala. Indexering åstadkoms i allmänhet med hjälp av en autoindexeringsrutin . Efter att ha tilldelats symmetri integreras data sedan . Detta konverterar de hundratals bilder som innehåller tusentals reflektioner till en enda fil, bestående av (åtminstone) poster av Miller-indexet för varje reflektion, och en intensitet för varje reflektion (i detta tillstånd innehåller filen ofta också feluppskattningar och mått på partialitet (vilken del av en given reflektion som registrerades på den bilden)).

En fullständig datamängd kan bestå av hundratals separata bilder tagna med olika orienteringar av kristallen. Det första steget är att slå samman och skala dessa olika bilder, det vill säga att identifiera vilka toppar som visas i två eller flera bilder ( sammanslagning ) och att skala de relativa bilderna så att de har en konsekvent intensitetsskala. Att optimera intensitetsskalan är kritisk eftersom den relativa intensiteten av topparna är nyckelinformationen från vilken strukturen bestäms. Den repetitiva tekniken för insamling av kristallografisk data och den ofta höga symmetrin hos kristallina material gör att diffraktometern registrerar många symmetriekvivalenta reflektioner flera gånger. Detta gör det möjligt att beräkna den symmetrirelaterade R-faktorn , ett tillförlitlighetsindex baserat på hur lika de uppmätta intensiteterna av symmetriekvivalenta reflektioner är, [ och därmed bedöma kvaliteten på data.

Inledande fasning

Ytterligare information: Fasproblem

Data som samlats in från ett diffraktionsexperiment är en reciprok rymdrepresentation av kristallgittret. Positionen för varje diffraktions-"fläck" styrs av storleken och formen på enhetscellen, och den inneboende symmetrin i kristallen. Intensiteten för varje diffraktionspunkt registreras, och denna intensitet är proportionell mot kvadraten på strukturfaktoramplituden . Strukturfaktorn är ett komplext tal som innehåller information om både amplituden och fasen för en våg . För att erhålla en tolkbar elektrondensitetskarta måste både amplitud och fas vara kända (en elektrondensitetskarta tillåter en kristallograf att bygga en startmodell av molekylen). Fasen kan inte registreras direkt under ett diffraktionsexperiment: detta är känt som fasproblemet . Initialfasuppskattningar kan erhållas på en mängd olika sätt:

• Ab initio -fasning eller direkta metoder – Detta är vanligtvis den valda metoden för små molekyler (<1000 icke-väteatomer), och har använts framgångsrikt för att lösa fasproblemen för små proteiner. Om upplösningen av data är bättre än 1,4 Å (140 pm ) kan direkta metoder användas för att erhålla fasinformation, genom att utnyttja kända fasförhållanden mellan vissa grupper av reflektioner.
• Molekylär ersättning – om en relaterad struktur är känd kan den användas som en sökmodell vid molekylär ersättning för att bestämma orienteringen och positionen för molekylerna i enhetscellen. Faserna som erhålls på detta sätt kan användas för att generera elektrondensitetskartor.
• Anomal röntgenspridning ( MAD eller SAD fasning ) – röntgenvåglängden kan skannas förbi en absorptionskant [ av en atom, vilket ändrar spridningen på känt sätt. Genom att registrera hela uppsättningar av reflektioner vid tre olika våglängder (långt under, långt ovanför och i mitten av absorptionskanten) kan man lösa understrukturen hos de anomalt diffraktionsatomer och därmed hela molekylens struktur. Den mest populära metoden för att införliva anomala spridningsatomer i proteiner är att uttrycka proteinet i en metionin- auxotrof (en värd som inte kan syntetisera metionin) i ett medium rikt på selenmetionin, som innehåller selenatomer . Ett multi-wavelength anomalous dispersion (MAD) experiment kan sedan utföras runt absorptionskanten, som sedan bör ge positionen för eventuella metioninrester i proteinet, vilket ger initiala faser.
• Tungatommetoder ( multipel isomorf ersättning ) – Om elektrontäta metallatomer kan införas i kristallen, kan direkta metoder eller Patterson-rymdmetoder användas för att bestämma deras placering och för att erhålla initiala faser. Sådana tunga atomer kan införas antingen genom att kristallen blötläggs i en lösning som innehåller tunga atomer eller genom samkristallisation (tillväxt av kristallerna i närvaro av en tung atom). Liksom vid anomal dispersionsfasning med flera våglängder kan förändringarna i spridningsamplituderna tolkas för att ge faserna. Även om detta är den ursprungliga metoden med vilken proteinkristallstrukturer löstes, har den i stort sett ersatts av avvikande dispersionsfasning med flera våglängder med selenometionin.

Modellbyggnad och fasförfining

Struktur av en protein alfa-helix, med stick-figurer för den kovalenta bindningen inom elektrondensitet för kristallstrukturen vid ultrahög upplösning (0,91 Å). Densitetskonturerna är i grått, spiralryggraden i vitt, sidokedjor i cyan, O-atomer i rött, N-atomer i blått och vätebindningar som gröna prickade linjer.

3D-bild av elektrondensitet (blå) för en ligand (orange) bunden till ett bindningsställe i ett protein (gult). Elektrondensiteten erhålls från experimentella data, och liganden modelleras till denna elektrondensitet.

Ytterligare information: Molekylär modellering

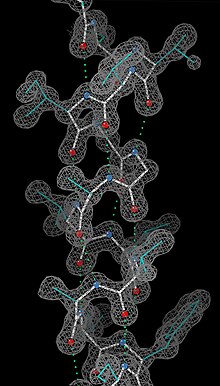
Efter att ha erhållit inledande faser kan en initial modell byggas. Atompositionerna i modellen och deras respektive Debye-Waller-faktorer (eller B -faktorer, som står för atomens termiska rörelse) kan förfinas för att passa de observerade diffraktionsdata, vilket idealiskt ger en bättre uppsättning faser. En ny modell kan sedan anpassas till den nya elektrondensitetskartan och successiva omgångar av förfining genomförs. Denna iterativa process fortsätter tills korrelationen mellan diffraktionsdata och modellen är maximerad. Överenskommelsen mäts med en R -faktor definierad som

$R={\frac {\sum _{\text{alla reflektioner}}\left|F_{\text{obs}}-F_{\text{calc}}\right|}{\sum _{ \text{alla reflektioner}}\left|F_{\text{obs}}\right|}},$

där F är strukturfaktorn . Ett liknande kvalitetskriterium är R _free , som beräknas från en delmängd (~10%) av reflektioner som inte ingick i strukturförfiningen. Båda R -faktorerna beror på dataupplösningen. Som en tumregel R _fri vara ungefär upplösningen i ångström dividerat med 10; således bör en datamängd med 2 Å upplösning ge en slutlig R _fri ~ 0,2. Kemiska bindningsegenskaper som stereokemi, vätebindning och fördelning av bindningslängder och vinklar är komplementära mått på modellkvaliteten. Fasbias är ett allvarligt problem vid sådan iterativ modellbyggnad. Utelämna kartor är en vanlig teknik som används för att kontrollera detta.

Det kanske inte är möjligt att observera varje atom i den asymmetriska enheten. I många fall kristallografisk störning ut elektrondensitetskartan. Svagt spridande atomer som väte är rutinmässigt osynliga. Det är också möjligt för en enskild atom att förekomma flera gånger i en elektrondensitetskarta, t.ex. om en proteinsidokedja har flera (<4) tillåtna konformationer. I ytterligare andra fall kan kristallografen upptäcka att den kovalenta strukturen som härleddes för molekylen var felaktig eller ändrad. Till exempel kan proteiner klyvas eller genomgå posttranslationella modifieringar som inte detekterades före kristalliseringen.

Oordning

Huvudartikel: kristallografisk störning

En vanlig utmaning vid förfining av kristallstrukturer är resultatet av kristallografisk störning. Störning kan ta många former men involverar i allmänhet samexistens av två eller flera arter eller konformationer. Att inte känna igen störningen leder till felaktig tolkning. Fallgropar från felaktig modellering av störningar illustreras av den diskonterade hypotesen om bindningssträckisomerism . Störning modelleras med avseende på den relativa populationen av komponenterna, ofta bara två, och deras identitet. I strukturer av stora molekyler och joner är lösningsmedel och motjoner ofta störda.

Tillämpad beräkningsdataanalys

Användningen av beräkningsmetoder för analys av pulverröntgendiffraktionsdata är nu generaliserad. Den jämför typiskt experimentella data med det simulerade diffraktogrammet för en modellstruktur, med hänsyn till de instrumentella parametrarna, och förfinar modellens strukturella eller mikrostrukturella parametrar med hjälp av minsta kvadraters minimeringsalgoritm. De flesta tillgängliga verktyg som tillåter fasidentifiering och strukturell förfining är baserade på Rietveld-metoden , några av dem är öppna och fri programvara som FullProf Suite, Jana2006, MAUD, Rietan, GSAS, etc. medan andra är tillgängliga under reklamlicenser som Diffrac. Suite TOPAS, Match!, etc. De flesta av dessa verktyg tillåter också Le Bail- förfining (även kallad profilmatchning), det vill säga förfining av cellparametrarna baserat på Bragg-topparnas positioner och toppprofiler, utan att ta hänsyn till den kristallografiska struktur i sig. Nyare verktyg tillåter förfining av både strukturella och mikrostrukturella data, såsom FAULTS-programmet som ingår i FullProf Suite, som tillåter förfining av strukturer med plana defekter (t.ex. staplingsfel, tvillingar, sammanväxter).

Avsättning av strukturen

När modellen för en molekyls struktur har slutförts, deponeras den ofta i en kristallografisk databas som Cambridge Structural Database (för små molekyler), Inorganic Crystal Structure Database (ICSD) (för oorganiska föreningar) eller Protein Data Bank ( för protein och ibland nukleinsyror). Många strukturer som erhållits i privata kommersiella satsningar för att kristallisera medicinskt relevanta proteiner deponeras inte i offentliga kristallografiska databaser.

Diffraktionsteori

Ytterligare information: Dynamisk teori om diffraktion och Bragg diffraktion

Huvudmålet med röntgenkristallografi är att bestämma tätheten av elektroner f ( r ) i hela kristallen, där r representerar den tredimensionella positionsvektorn i kristallen. För att göra detta används röntgenspridning för att samla in data om dess Fouriertransform F ( q ), som inverteras matematiskt för att erhålla densiteten definierad i det verkliga rummet, med hjälp av formeln

$f(\mathbf {r} )={\frac {1}{\left(2\pi \ höger)^{3}}}\int F(\mathbf {q} )e^{\mathrm {i} \mathbf {q} \cdot \mathbf {r} }\mathrm {d} \mathbf {q} ,$

där integralen tas över alla värden på q . Den tredimensionella reella vektorn q representerar en punkt i det reciproka rymden , det vill säga till en viss svängning i elektrontätheten när man rör sig i den riktning i vilken q pekar. Längden på q motsvarar $2\pi$ dividerat med svängningens våglängd. Motsvarande formel för en Fouriertransform kommer att användas nedan

$F(\mathbf {q} )=\int f(\mathbf {r} )\mathrm {e} ^{-\ mathrm {i} \mathbf {q} \cdot \mathbf {r} }\mathrm {d} \mathbf {r} ,$

där integralen summeras över alla möjliga värden för positionsvektorn r i kristallen.

Fouriertransformen F ( q ) är i allmänhet ett komplext tal och har därför en storlek | F ( q )| och en fas φ ( q ) relaterad av ekvationen

$F(\mathbf {q} )=\left|F(\mathbf {q} )\right|\mathrm {e} ^{\mathrm {i} \phi (\mathbf {q} )}.$

Intensiteterna för de reflektioner som observeras i röntgendiffraktion ger oss magnituderna | F ( q )| men inte faserna φ ( q ). För att erhålla faserna samlas hela uppsättningar av reflektioner med kända förändringar av spridningen, antingen genom att modulera våglängden förbi en viss absorptionskant eller genom att lägga till starkt spridande (dvs elektrontäta) metallatomer som kvicksilver . Kombination av magnituderna och faserna ger den fullständiga Fouriertransformen F ( q ), som kan inverteras för att erhålla elektrondensiteten f ( r ).

Kristaller idealiseras ofta som att de är perfekt periodiska. I det ideala fallet är atomerna placerade på ett perfekt gitter, elektrontätheten är perfekt periodisk och Fouriertransformen F ( q ) är noll förutom när q tillhör det reciproka gittret (de så kallade Bragg-topparna ). I verkligheten är dock kristaller inte helt periodiska; atomer vibrerar kring sin genomsnittliga position, och det kan finnas oordning av olika typer, såsom mosaicitet , dislokationer , olika punktdefekter och heterogenitet i konformationen av kristalliserade molekyler. Därför har Bragg-topparna en ändlig bredd och det kan finnas betydande diffus spridning , ett kontinuum av spridda röntgenstrålar som faller mellan Bragg-topparna.

Intuitiv förståelse av Braggs lag

En intuitiv förståelse av röntgendiffraktion kan erhållas från Bragg-modellen för diffraktion . I denna modell är en given reflektion associerad med en uppsättning jämnt fördelade ark som löper genom kristallen, vanligtvis passerar genom mitten av atomerna i kristallgittret. Orienteringen av en viss uppsättning ark identifieras av dess tre Miller-index ( h , k , l ), och låt deras avstånd noteras med d . William Lawrence Bragg föreslog en modell där de inkommande röntgenstrålarna sprids spegelblankt (spegellikt) från varje plan; från det antagandet kommer röntgenstrålar spridda från intilliggande plan att kombineras konstruktivt ( konstruktiv interferens ) när vinkeln θ mellan planet och röntgenstrålningen resulterar i en banlängdsskillnad som är en heltalsmultipel n av röntgenvåglängden λ .

$2d\sin \theta =n\lambda .$

En reflektion sägs vara indexerad när dess Miller-index (eller, mer korrekt, dess reciproka gittervektorkomponenter) har identifierats från den kända våglängden och spridningsvinkeln 2θ. Sådan indexering ger enhetscellparametrarna , längderna och vinklarna för enhetscellen samt dess rymdgrupp . Eftersom Braggs lag inte tolkar de relativa intensiteterna av reflektionerna, är det emellertid i allmänhet otillräckligt att lösa för arrangemanget av atomer inom enhetscellen; för det måste en Fourier-transformmetod utföras.

Spridning som en Fouriertransform

Den inkommande röntgenstrålen har en polarisation och bör representeras som en vektorvåg; låt den dock för enkelhets skull representeras här som en skalär våg. Vi ignorerar också komplikationen av vågens tidsberoende och koncentrerar oss bara på vågens rumsliga beroende. Plana vågor kan representeras av en vågvektor k _in , så styrkan på den inkommande vågen vid tidpunkten t = 0 ges av

$A\mathrm {e} ^{\mathrm {i} \mathbf {k} _{\mathrm {in} }\cdot \mathbf {r} }.$

Vid position r inom provet, låt det finnas en täthet av spridare f ( r ); dessa spridare bör producera en spridd sfärisk våg med amplitud proportionell mot den lokala amplituden för den inkommande vågen gånger antalet spridare i en liten volym dV ca r

${\text{amplitud av spridd våg}}=A\mathrm {e} ^{\mathrm {i} \mathbf {k } \cdot \mathbf {r} }Sf(\mathbf {r} )\mathrm {d} V,$

där S är proportionalitetskonstanten.

Betrakta bråkdelen av spridda vågor som lämnar med en utgående våg-vektor på k _ut och träffar skärmen på r _skärmen . Eftersom ingen energi går förlorad (elastisk, inte oelastisk spridning), är våglängderna desamma som storleken på vågvektorerna | k _i |=| k _ut |. Från det att fotonen sprids vid r tills den absorberas vid r _skärmen genomgår fotonen en fasförändring

$e^{i\mathbf {k} _{\text{out}}\cdot \left(\mathbf {r} _{\text{skärm}}-\mathbf {r} \right)}.$

Nettostrålningen som anländer till r _skärmen är summan av alla spridda vågor genom kristallen

$AS\int \mathrm {d} \mathbf {r} f(\mathbf {r} )\mathrm {e} ^{\mathrm {i} \mathbf {k} _{\text {in}}\cdot \mathbf {r} }e^{i\mathbf {k} _{\text{out}}\cdot \left(\mathbf {r} _{\text{skärm}}-\mathbf {r} \right)}=ASe^{i\mathbf {k} _{\text{out}}\cdot \mathbf {r} _{\text{skärm}}}\int \mathrm {d} \mathbf {r} f(\mathbf {r} )\mathrm {e} ^{\mathrm {i} \left(\mathbf {k} _{\text{i}}-\mathbf {k} _{\text{ ut}}\right)\cdot \mathbf {r} },$

som kan skrivas som en Fouriertransform

$AS\mathrm {e} ^{\mathrm {i} \mathbf {k} _{\text{out}}\cdot \mathbf {r} _{\text{skärm}}}\int d\mathbf {r} f(\mathbf {r} )\mathrm {e} ^{-\mathrm {i} \mathbf {q} \cdot \mathbf {r} }=AS\mathrm {e} ^{\mathrm {i} \mathbf {k} _{\text{out} }\cdot \mathbf {r} _{\text{skärm}}}F(\mathbf {q} ),$

där q = k _ut – k _in . Den uppmätta intensiteten av reflektionen kommer att vara kvadratisk av denna amplitud

$A^{2}S^{2}\left|F(\mathbf {q} )\right|^{2}.$

Friedel och Bijvoet kompisar

För varje reflektion som motsvarar en punkt q i det reciproka rummet, finns det ytterligare en reflektion av samma intensitet i den motsatta punkten - q . Denna motsatta reflektion är känd som den ursprungliga reflektionens Friedel-kompis . Denna symmetri beror på det matematiska faktum att tätheten av elektroner f ( r ) vid en position r alltid är ett reellt tal . Som noterats ovan f ( r ) den inversa transformationen av dess Fouriertransform F ( q ); emellertid är en sådan omvänd transform ett komplext tal i allmänhet. För att säkerställa att f ( r ) är reell måste Fouriertransformen F ( q ) vara sådan att Friedel-paren F (− q ) och F ( q ) är komplexa konjugat av varandra. F (− q ) har alltså samma storlek som F ( q ) men de har motsatt fas, dvs φ ( q ) = − φ ( -q )

$F(-\mathbf {q} )=\left|F(-\mathbf {q} )\right|\mathrm {e} ^{\mathrm {i} \phi (-\mathbf {q} ) }=F^{*}(\mathbf {q} )=\left|F(\mathbf {q} )\right|\mathrm {e} ^{-\mathrm {i} \phi (\mathbf {q} )}.$

Jämlikheten i deras storlek säkerställer att Friedel-kompisarna har samma intensitet | F | ² . Denna symmetri gör att man kan mäta hela Fouriertransformen från endast halva det reciproka utrymmet, t.ex. genom att rotera kristallen något mer än 180° istället för ett helt 360° varv. I kristaller med betydande symmetri kan ännu fler reflektioner ha samma intensitet (Bijvoet kompisar); i sådana fall kan ännu mindre av det reciproka utrymmet behöva mätas. I gynnsamma fall av hög symmetri krävs ibland bara 90° eller till och med bara 45° data för att helt utforska det ömsesidiga utrymmet.

Friedel-mate-begränsningen kan härledas från definitionen av den inversa Fouriertransformen

$f(\mathbf {r} )=\int {\frac {d\mathbf {q} }{\left(2\pi \right)^{3}}}F(\mathbf {q} )\ mathrm {e} ^{\mathrm {i} \mathbf {q} \cdot \mathbf {r} }=\int {\frac {d\mathbf {q} }{\left(2\pi \right)^{ 3}}}\left|F(\mathbf {q} )\right|\mathrm {e} ^{\mathrm {i} \phi (\mathbf {q} )}\mathrm {e} ^{\mathrm { i} \mathbf {q} \cdot \mathbf {r} }.$

Eftersom Eulers formel säger att e ^{i x} = cos( x ) + i sin( x ), kan den inversa Fouriertransformen delas upp i en summa av en rent reell del och en rent imaginär del

$f(\mathbf {r} )=\int {\frac {d\mathbf {q} }{\left(2\pi \right)^{3}}}\left|F(\mathbf {q } )\right|\mathrm {e} ^{\mathrm {i} \left(\phi +\mathbf {q} \cdot \mathbf {r} \right)}=\int {\frac {d\mathbf { q} }{\left(2\pi \right)^{3}}}\left|F(\mathbf {q} )\right|\cos \left(\phi +\mathbf {q} \cdot \mathbf {r} \right)+i\int {\frac {d\mathbf {q} }{\left(2\pi \right)^{3}}}\left|F(\mathbf {q} )\right |\sin \left(\phi +\mathbf {q} \cdot \mathbf {r} \right)=I_{\mathrm {cos} }+iI_{\mathrm {sin} }.$

Funktionen f ( r ) är reell om och endast om den andra integralen I _sin är noll för alla värden på r . I sin tur är detta sant om och endast om ovanstående begränsning är uppfylld

$I_{\sin }=\int {\frac {d\mathbf {q} }{\left(2\pi \right)^{3 }}}\left|F(\mathbf {q} )\right|\sin \left(\phi +\mathbf {q} \cdot \mathbf {r} \right)=\int {\frac {d\mathbf {q} }{\left(2\pi \right)^{3}}}\left|F(\mathbf {-q} )\right|\sin \left(-\phi -\mathbf {q} \ cdot \mathbf {r} \right)=-I_{\sin },$

eftersom jag _syndar = − Jag _syndar innebär att jag _syndar = 0.

Ewalds sfär

Ytterligare information: Ewalds sfär

Representation av en Ewald-konstruktion som visar en incident ( ${\displaystyle {\overrightarrow {k_{b}}}} )$ , spridd ( ${\overrightarrow {k_{b}'}}$ ) , och resulterande vågvektor ( ${\displaystyle {\overrightarrow {\Delta k}}})$ . Eftersom det finns en resulterande vågvektor genererad mellan två reciproka gitterpunkter, kommer diffraktion att tillåtas eftersom den resulterande vågvektorn kommer att uppfylla villkoren för en "reciprok gittervektor".

Varje röntgendiffraktionsbild representerar endast en skiva, en sfärisk skiva av reciprokt utrymme, vilket kan ses av Ewald-sfärkonstruktionen. Både k _out och k _in har samma längd, på grund av den elastiska spridningen, eftersom våglängden inte har förändrats. Därför kan de representeras som två radiella vektorer i en sfär i reciprokt utrymme , som visar värdena på q som samplas i en given diffraktionsbild. Eftersom det finns en liten spridning i de inkommande våglängderna för den inkommande röntgenstrålen, är värdena för| F ( q )|kan endast mätas för q- vektorer placerade mellan de två sfärerna som motsvarar dessa radier. För att erhålla en fullständig uppsättning Fourier-transformationsdata är det därför nödvändigt att rotera kristallen något mer än 180°, eller ibland mindre om tillräcklig symmetri är närvarande. En hel 360° rotation behövs inte på grund av en symmetri som är inneboende i Fouriertransformerna av reella funktioner (såsom elektrondensiteten), men "något mer" än 180° behövs för att täcka hela det reciproka utrymmet inom en given upplösning på grund av Ewaldsfärens krökning . I praktiken vaggas kristallen en liten mängd (0,25–1°) för att införliva reflektioner nära gränserna för det sfäriska Ewalds skal.

Patterson funktion

Ytterligare information: Patterson-funktion

Ett välkänt resultat av Fouriertransformer är autokorrelationssatsen, som säger att autokorrelationen c ( r ) för en funktion f ( r )

$c(\mathbf {r} )=\int d\mathbf {x} f(\mathbf {x} )f(\mathbf {x} +\mathbf {r} )=\int {\frac {d\mathbf {q} }{\left(2\pi \ höger)^{3}}}C(\mathbf {q} )e^{i\mathbf {q} \cdot \mathbf {r} }$

har en Fouriertransform C ( q ) som är den kvadratiska storleken på F ( q )

$C(\mathbf {q} )=\left|F(\mathbf {q} )\right|^{2}.$

Därför kan autokorrelationsfunktionen c ( r ) för elektrondensiteten (även känd som Patterson-funktionen ) beräknas direkt från reflektionsintensiteterna, utan att beräkna faserna. I princip skulle detta kunna användas för att bestämma kristallstrukturen direkt; det är dock svårt att inse i praktiken. Autokorrelationsfunktionen motsvarar fördelningen av vektorer mellan atomer i kristallen; sålunda kan en kristall av N- atomer i sin enhetscell ha N ( N - 1) toppar i sin Patterson-funktion. Med tanke på de oundvikliga felen i att mäta intensiteterna och de matematiska svårigheterna att rekonstruera atompositioner från de interatomära vektorerna, används denna teknik sällan för att lösa strukturer, förutom de enklaste kristallerna.

Fördelar med en kristall

I princip kan en atomstruktur bestämmas genom att applicera röntgenspridning på icke-kristallina prover, till och med på en enda molekyl. Emellertid ger kristaller en mycket starkare signal på grund av deras periodicitet. Ett kristallint prov är per definition periodiskt; en kristall består av många enhetsceller som upprepas oändligt i tre oberoende riktningar. Sådana periodiska system har en Fouriertransform som är koncentrerad till periodiskt upprepade punkter i reciproka rymden som kallas Bragg-toppar ; Bragg-topparna motsvarar reflektionsfläckarna som observeras i diffraktionsbilden. Eftersom amplituden vid dessa reflektioner växer linjärt med antalet N spridare, bör den observerade intensiteten hos dessa fläckar växa kvadratiskt, som N ² . Med andra ord, att använda en kristall koncentrerar den svaga spridningen av de individuella enhetscellerna till en mycket kraftfullare, sammanhängande reflektion som kan observeras ovanför bruset. Detta är ett exempel på konstruktiv interferens .

I ett vätske-, pulver- eller amorft prov är molekylerna i provet i slumpmässig orientering. Sådana sampel har ett kontinuerligt Fourier-spektrum som likformigt sprider sin amplitud och därigenom minskar den uppmätta signalintensiteten, vilket observeras i SAXS . Ännu viktigare är att den orienterande informationen går förlorad. Även om det är teoretiskt möjligt, är det experimentellt svårt att erhålla atomupplösningsstrukturer av komplicerade, asymmetriska molekyler från sådana rotationsmedelvärdesdata. Ett mellanfall är fiberdiffraktion där subenheterna är arrangerade periodiskt i åtminstone en dimension.

Nobelpris som involverar röntgenkristallografi

År	Pristagare	Pris	Logisk grund
1914	Max von Laue	Fysik	"För hans upptäckt av diffraktionen av röntgenstrålar genom kristaller", ett viktigt steg i utvecklingen av röntgenspektroskopi .
1915	William Henry Bragg	Fysik	"För deras tjänster inom analys av kristallstruktur med hjälp av röntgenstrålar"
	William Lawrence Bragg
1962	Max F. Perutz	Kemi	"för sina studier av strukturerna hos klotformiga proteiner "
	John C. Kendrew
1962	James Dewey Watson	Medicin	nukleinsyrors molekylära struktur och dess betydelse för informationsöverföring i levande material"
	Francis Harry Compton Crick
	Maurice Hugh Frederick Wilkins
1964	Dorothy Hodgkin	Kemi	"För hennes bestämningar med röntgentekniker av strukturerna hos viktiga biokemiska ämnen"
1972	Stanford Moore	Kemi	"För deras bidrag till förståelsen av sambandet mellan kemisk struktur och katalytisk aktivitet hos ribonukleasmolekylens aktiva centrum "
	William H. Stein
1976	William N. Lipscomb	Kemi	"För hans studier om strukturen hos boraner som belyser problem med kemisk bindning"
1985	Jerome Karle	Kemi	"För deras enastående prestationer i att utveckla direkta metoder för bestämning av kristallstrukturer"
	Herbert A. Hauptman
1988	Johann Deisenhofer	Kemi	"För deras bestämning av den tredimensionella strukturen hos ett fotosyntetiskt reaktionscentrum "
	Hartmut Michel	Kemi
	Robert Huber	Kemi
1997	John E. Walker	Kemi	"För deras förtydligande av den enzymatiska mekanismen som ligger till grund för syntesen av adenosintrifosfat (ATP)"
2003	Roderick MacKinnon	Kemi	"För upptäckter rörande kanaler i cellmembran [...] för strukturella och mekanistiska studier av jonkanaler "
	Peter Agre		"För upptäckter rörande kanaler i cellmembran [...] för upptäckt av vattenkanaler "
2006	Roger D. Kornberg	Kemi	"För hans studier av den molekylära basen för eukaryot transkription "
2009	Ada E. Yonath	Kemi	ribosomens struktur och funktion "
	Thomas A. Steitz
	Venkatraman Ramakrishnan
2012	Brian Kobilka	Kemi	"För studier av G-proteinkopplade receptorer "

Ansökningar

Röntgendiffraktion har breda och olika tillämpningar inom de kemiska, biokemiska, fysikaliska, material- och mineralogiska vetenskaperna. Laue hävdade 1937 att tekniken "har utökat förmågan att observera minutstruktur tiotusen gånger utöver det som mikroskopet ger oss". Röntgendiffraktion är analog med ett mikroskop med upplösning på atomnivå som visar atomerna och deras elektronfördelning.

Röntgendiffraktion, elektrondiffraktion och neutrondiffraktion ger information om strukturen hos materia, kristallin och icke-kristallin, på atomär och molekylär nivå. Dessutom kan dessa metoder tillämpas vid studiet av egenskaper hos alla material, oorganiska, organiska eller biologiska. På grund av vikten och mångfalden av tillämpningar av diffraktionsstudier av kristaller har många Nobelpriser delats ut för sådana studier.

Läkemedelsidentifiering

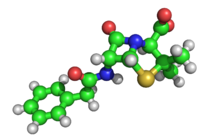
Röntgendiffraktion har använts för identifiering av antibiotikaläkemedel såsom: åtta β-laktam ( ampicillinnatrium , penicillin G prokain , cefalexin , ampicillin trihydrat, bensatin penicillin , bensylpenicillinnatrium , cefotaxim natrium , cefotaxim natrium teoxin Ceft, ricyklin treaxon natrium , hydroklorid , oxytetracyklindehydrat , tetracyklinhydroklorid ) och två makrolid- ( azitromycin , erytromycinestolat ) antibiotika. Vart och ett av dessa läkemedel har ett unikt röntgendiffraktionsmönster (XRD) som gör deras identifiering möjlig.

Karakterisering av nanomaterial, textilfibrer och polymerer

Forensisk undersökning av spårbevis är baserad på Locards utbytesprincip . Där står det att "varje kontakt lämnar spår". I praktiken kan det, även om en överföring av material har skett, vara omöjligt att upptäcka, eftersom det överförda beloppet är mycket litet.

XRD har bevisat sin roll i utvecklingen av nanomaterialforskning. Det är ett av de primära karaktäriseringsverktygen och ger information om de strukturella egenskaperna hos olika nanomaterial i både pulver- och tunnfilmsform.

Textilfibrer är en blandning av kristallina och amorfa ämnen. Därför ger mätningen av graden av kristallin användbara data vid karakterisering av fibrer med användning av röntgendiffraktometri. Det har rapporterats att röntgendiffraktion användes för att identifiera en "kristallin" avsättning som hittades på en stol. Avsättningen visade sig vara amorf, men det närvarande diffraktionsmönstret matchade det för polymetylmetakrylat. Pyrolysmasspektrometri identifierade senare avsättningen som polymetylcyanoakrylaon av Boin-kristallparametrar .

Integrerade kretsar

Röntgendiffraktion har visats som en metod för att undersöka den komplexa strukturen hos integrerade kretsar .

Se även

• Beevers–Lipson strip
• Bragg diffraktion
• Kristallografisk databas
• Kristallografiska punktgrupper
• Skillnadstäthetskarta
• Elektrondiffraktion
• Energidispersiv röntgendiffraktion
• Flack parameter
• Henderson gräns
• Internationella kristallografiåret
• John Desmond Bernal
• Multipoldensitetsformalism
• Neutrondiffraktion
• Pulverdiffraktion
• Ptychografi
• Scherrer ekvation
• Röntgenspridning med liten vinkel (SAXS)
• Strukturbestämning
• Ultrasnabb röntgen
• Vidvinkelröntgenspridning (WAXS)

Vidare läsning

Internationella tabeller för kristallografi

•   Hahn T, red. (2002). Internationella tabeller för kristallografi. Volym A, Space-group Symmetry (5:e upplagan). Dordrecht: Kluwer Academic Publishers , för International Union of Crystallography . ISBN 0-7923-6590-9 .
•   Rossmann MG, Arnold E, red. (2001). Internationella tabeller för kristallografi. Volym F, Kristallografi av biologiska molekyler . Dordrecht: Kluwer Academic Publishers, för International Union of Crystallography. ISBN 0-7923-6857-6 .
•   Hahn T, red. (1996). Internationella tabeller för kristallografi. Brief Teaching Edition av volym A, Space-group Symmetry (4:e upplagan). Dordrecht: Kluwer Academic Publishers, för International Union of Crystallography. ISBN 0-7923-4252-6 .

Inbundna artikelsamlingar

•   Carter Jr CW, Sweet RM, red. (1997). Macromolecular Crystallography, del A (Methods in Enzymology, v. 276) . San Diego: Academic Press. ISBN 0-12-182177-3 .
•   Carter Jr CW, Sweet RM, red. (1997). Macromolecular Crystallography, del B (Methods in Enzymology, v. 277) . San Diego: Academic Press. ISBN 0-12-182178-1 .
•   Ducruix A, Giegé R, red. (1999). Kristallisering av nukleinsyror och proteiner: A Practical Approach (2:a upplagan). Oxford: Oxford University Press. ISBN 0-19-963678-8 .

Läroböcker

•   Birkholz M, Fewster PF, Genzel C (2005). "Kapitel 1: Principer_för_röntgendiffraktion" . Tunnfilmsanalys genom röntgenspridning . Weinheim: Wiley-VCH. ISBN 978-3-527-31052-4 .
•   Blow D (2002). Översikt över kristallografi för biologer . Oxford: Oxford University Press. ISBN 0-19-851051-9 .
•   Burns G, Glazer AM (1990). Space Groups for Scientists and Engineers (2nd ed.). Boston: Academic Press, Inc. ISBN 0-12-145761-3 .
•   Clegg W (1998). Kristallstrukturbestämning (Oxford Chemistry Primer) . Oxford: Oxford University Press. ISBN 0-19-855901-1 .
•   Culity BD (1978). Elements of X-Ray Diffraction (2:a upplagan). Reading, Massachusetts: Addison-Wesley Publishing Company. ISBN 0-534-55396-6 .
•   Drenth J (1999). Principer för proteinröntgenkristallografi . New York: Springer-Verlag. ISBN 0-387-98587-5 .
•   Giacovazzo C (1992). Kristallografins grunder . Oxford: Oxford University Press. ISBN 0-19-855578-4 .
•   Glusker JP, Lewis M, Rossi M (1994). Kristallstrukturanalys för kemister och biologer . New York: VCH Publishers. ISBN 0-471-18543-4 .
•   Massa W (2004). Bestämning av kristallstruktur . Berlin: Springer. ISBN 3-540-20644-2 .
•   McPherson A (1999). Kristallisering av biologiska makromolekyler . Cold Spring Harbor, NY: Cold Spring Harbor Laboratory Press. ISBN 0-87969-617-6 .
•   McPherson A (2003). Introduktion till makromolekylär kristallografi . John Wiley & Sons. ISBN 0-471-25122-4 .
•   McRee DE (1993). Praktisk proteinkristallografi . San Diego: Academic Press. ISBN 0-12-486050-8 .
•   O'Keeffe M, Hyde BG (1996). Kristallstrukturer; I. Mönster och symmetri . Washington, DC: Mineralogical Society of America, Monograph Series. ISBN 0-939950-40-5 .
•   Rhodes G (2000). Kristallografi gjorde kristallklart . San Diego: Academic Press. ISBN 0-12-587072-8 . , PDF-kopia av utvalda kapitel
•   Rupp B (2009). Biomolekylär kristallografi: principer, praxis och tillämpning på strukturbiologi . New York: Garland Science. ISBN 978-0-8153-4081-2 .
•   Warren BE (1969). Röntgendiffraktion . New York. ISBN 0-486-66317-5 .
•   Zachariasen WH (1945). Teori om röntgendiffraktion i kristaller . New York: Dover Publications. LCCN 67026967 .

Tillämpad beräkningsdataanalys

•   Young RA, red. (1993). Rietveldmetoden . Oxford: Oxford University Press & International Union of Crystallography. ISBN 0-19-855577-6 .

Historisk

• Bijvoet MJ , Burgers WG, Hägg G, red. (1969). Tidiga artiklar om diffraktion av röntgenstrålar av kristaller . Vol. I. Utrecht: publicerad för International Union of Crystallography av A. Oosthoek's Uitgeversmaatschappij NV
• Bijvoet JM, Burgers WG, Hägg G, red. (1972). Tidiga artiklar om diffraktion av röntgenstrålar av kristaller . Vol. II. Utrecht: publicerad för International Union of Crystallography av A. Oosthoek's Uitgeversmaatschappij NV
•   Bragg WL, Phillips DC, Lipson H (1992). Utvecklingen av röntgenanalys . New York: Dover. ISBN 0-486-67316-2 .
•   Ewald PP , et al., red. (1962). Femtio år av röntgendiffraktion . Utrecht: publicerad för International Union of Crystallography av A. Oosthoek's Uitgeversmaatschappij NV doi : 10.1007/978-1-4615-9961-6 . ISBN 978-1-4615-9963-0 .
• Ewald PP (red.). "50 år av röntgendiffraktion" . International Union of Crystallography. Omtryckt i pdf-format för IUCr XVIII Congress, Glasgow, Skottland
•   Friedrich W (1922). "Die Geschichte der Auffindung der Röntgenstrahlinterferenzen" . Die Naturwissenschaften . 10 (16): 363. Bibcode : 1922NW.....10..363F . doi : 10.1007/BF01565289 . S2CID 28141506 .
• Lonsdale K (1949). Kristaller och röntgenstrålar . New York: D. van Nostrand.

externa länkar

Handledningar

• Lär dig kristallografi
• Enkel, icke-teknisk introduktion
• The Crystallography Collection , videoserie från Royal Institution
• "Small Molecule Crystalization" ( PDF ) på Illinois Institute of Technologys webbplats
• International Union of Crystallography
• Kristallografi 101
• Handledning för interaktiv strukturfaktor , som visar egenskaperna hos diffraktionsmönstret för en 2D-kristall.
• Picturebook of Fourier Transforms , som illustrerar förhållandet mellan kristall och diffraktionsmönster i 2D.
• Föreläsningsanteckningar om röntgenkristallografi och strukturbestämning
• Onlineföreläsning om moderna röntgenspridningsmetoder för materialanalys i nanoskala av Richard J. Matyi
• Interactive Crystallography Timeline Arkiverad 2021-06-30 på Wayback Machine från Royal Institution

Primära databaser

• Kristallografi öppen databas (COD)
• Protein Data Bank ( PDB )
• Nukleinsyradatabank (NDB)
• Cambridge Structural Database ( CSD )
• Databas för oorganisk kristallstruktur ( ICSD )
• Biologisk makromolekylkristalliseringsdatabas (BMCD)

Derivatdatabaser

• PDBsumma
• Proteopedia – det samarbetande 3D-uppslagsverket av proteiner och andra molekyler
• RNABase
• HIC-Up-databas med PDB-ligander Arkiverad 2020-08-08 på Wayback Machine
• Databas för strukturell klassificering av proteiner
• CATH proteinstrukturklassificering
• Lista över transmembranproteiner med känd 3D-struktur Arkiverad 2011-04-11 på Wayback Machine
• Orientering av proteiner i membrandatabas

Strukturell validering

• MolProbity strukturell valideringssvit
• ProSA-webb
• NQ-Flipper (kontrollera om det finns ogynnsamma rotamerer av Asn- och Gln-rester)
• DALI-server (identifierar proteiner som liknar ett givet protein)