Kristallstruktur

Kristallstruktur av bordssalt (natrium i lila, klor i grönt)

I kristallografi är kristallstruktur en beskrivning av det ordnade arrangemanget av atomer , joner eller molekyler i ett kristallint material . Ordnade strukturer uppstår från den inneboende naturen hos de ingående partiklarna för att bilda symmetriska mönster som upprepas längs de huvudsakliga riktningarna för det tredimensionella rummet i materien.

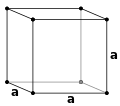
Den minsta gruppen av partiklar i materialet som utgör detta upprepande mönster är enhetscellen i strukturen. Enhetscellen återspeglar helt symmetrin och strukturen hos hela kristallen, som byggs upp genom upprepad translation av enhetscellen längs dess huvudaxlar. Översättningsvektorerna definierar noderna för Bravais-gittret .

Längden på enhetscellens huvudaxlar, eller kanter, och vinklarna mellan dem är gitterkonstanterna, även kallade gitterparametrar eller cellparametrar . Kristallens symmetriegenskaper beskrivs av begreppet rymdgrupper . Alla möjliga symmetriska arrangemang av partiklar i tredimensionellt rymd kan beskrivas av de 230 rymdgrupperna.

Kristallstrukturen och symmetrin spelar en avgörande roll för att bestämma många fysiska egenskaper, såsom klyvning , elektronisk bandstruktur och optisk transparens .

Enhetscell

Huvudartikel: Enhetscell

Kristallstrukturen beskrivs i termer av geometrin för arrangemanget av partiklar i enhetscellerna. Enhetscellen definieras som den minsta repeterande enheten som har kristallstrukturens fulla symmetri. Enhetscellens geometri definieras som en parallellepiped , som tillhandahåller sex gitterparametrar som längden på cellkanterna ( a , b , c ) och vinklarna mellan dem (α, β, γ). Positionerna för partiklar inuti enhetscellen beskrivs av bråkkoordinaterna ( x _i , y _i , z _i ) längs cellkanterna, mätt från en referenspunkt. Det är således endast nödvändigt att rapportera koordinaterna för en minsta asymmetrisk delmängd av partiklar. Denna grupp av partiklar kan väljas så att den upptar det minsta fysiska utrymmet, vilket innebär att inte alla partiklar behöver vara fysiskt placerade innanför de gränser som ges av gitterparametrarna. Alla andra partiklar i enhetscellen genereras av de symmetrioperationer som kännetecknar enhetscellens symmetri. Samlingen av symmetrioperationer för enhetscellen uttrycks formellt som rymdgruppen för kristallstrukturen.

• 

  Enkel kubik (P)

• 

  Kroppscentrerad kubik (I)

• 

  Ansiktscentrerad kubik (F)

Miller index

Plan med olika Miller-index i kubiska kristaller

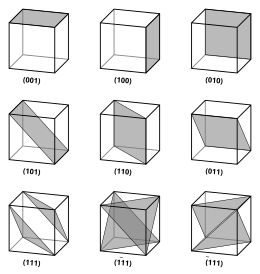
Vektorer och plan i ett kristallgitter beskrivs av Miller-indexnotationen med tre värden. Denna syntax använder indexen h , k och ℓ som riktningsparametrar.

Per definition betecknar syntaxen ( hkℓ ) ett plan som skär de tre punkterna a ₁ / h , a ₂ / k och en ₃ / ℓ , eller någon multipel därav. Det vill säga, Miller-indexen är proportionella mot inverserna av planets skärningar med enhetscellen (i basen av gittervektorerna). Om ett eller flera av indexen är noll betyder det att planen inte skär den axeln (dvs skärningen är "i oändligheten"). Ett plan som innehåller en koordinataxel översätts så att det inte längre innehåller den axeln innan dess Miller-index bestäms. Miller-indexen för ett plan är heltal utan gemensamma faktorer. Negativa index indikeras med horisontella staplar, som i (1 2 3). I ett ortogonalt koordinatsystem för en kubisk cell är Miller-indexen för ett plan de kartesiska komponenterna i en vektor normal mot planet.

Med tanke på endast ( hkℓ ) plan som skär en eller flera gitterpunkter (gitterplanen ) , är avståndet d mellan intilliggande gitterplan relaterat till den (kortaste) reciproka gittervektorn ortogonal mot planen med formeln

$d={\frac {2\pi }{|\mathbf {g} _{hk\ell }|}}$

Flygplan och vägbeskrivningar

De kristallografiska riktningarna är geometriska linjer som förbinder noder ( atomer , joner eller molekyler ) i en kristall. Likaså är de kristallografiska planen geometriska plan som länkar samman noder. Vissa riktningar och plan har en högre täthet av noder. Dessa högdensitetsplan har en inverkan på kristallens beteende enligt följande:

• Optiska egenskaper : Brytningsindex är direkt relaterat till densitet (eller periodiska densitetsfluktuationer).
• Adsorption och reaktivitet : Fysisk adsorption och kemiska reaktioner sker vid eller nära ytatomer eller molekyler. Dessa fenomen är således känsliga för tätheten av noder.
• Ytspänning : Kondensationen av ett material gör att atomerna, jonerna eller molekylerna är mer stabila om de omges av andra liknande arter. Ytspänningen hos ett gränssnitt varierar således beroende på densiteten på ytan.

Täta kristallografiska plan

• Mikrostrukturella defekter : Porer och kristalliter tenderar att ha raka korngränser efter plan med högre densitet.
• Klyvning : Detta sker vanligtvis företrädesvis parallellt med plan med högre densitet.
• Plastisk deformation : Dislokationsglid sker företrädesvis parallellt med plan med högre densitet. Störningen som bärs av dislokationen ( Burgers vektor ) är längs en tät riktning. Förskjutningen av en nod i en mer tät riktning kräver en mindre förvrängning av kristallgittret.

Vissa riktningar och plan definieras av kristallsystemets symmetri. I monokliniska, romboedriska, tetragonala och trigonala/hexagonala system finns det en unik axel (kallas ibland huvudaxeln) som har högre rotationssymmetri än de andra två axlarna. Basplanet är planet vinkelrätt mot huvudaxeln i dessa kristallsystem . För trikliniska, ortorombiska och kubiska kristallsystem är axelbeteckningen godtycklig och det finns ingen huvudaxel.

Kubiska strukturer

För specialfallet med enkla kubiska kristaller är gittervektorerna ortogonala och lika långa (vanligtvis betecknade a ) ; på liknande sätt för det ömsesidiga gittret. betecknar Miller-indexen ( ℓmn ) och [ ℓmn ] båda helt enkelt normaler/riktningar i kartesiska koordinater . För kubiska kristaller med gitterkonstant a är avståndet d mellan intilliggande (ℓmn) gitterplan (från ovan):

$d_{\ell mn}={\frac {a}{\sqrt {\ell ^{2}+m^{2}+n^{ 2}}}}$

På grund av symmetrin hos kubiska kristaller är det möjligt att ändra platsen och tecknet för heltalen och ha motsvarande riktningar och plan:

• Koordinater inom vinkelparenteser såsom ⟨100⟩ betecknar en familj av riktningar som är ekvivalenta på grund av symmetrioperationer, såsom [100], [010], [001] eller det negativa i någon av dessa riktningar.
• Koordinater inom parenteser eller klammerparenteser som {100} anger en familj av plannormaler som är ekvivalenta på grund av symmetrioperationer, ungefär som vinkelparenteser anger en familj av riktningar.

För ansiktscentrerade kubiska (fcc) och kroppscentrerade kubiska (bcc) gitter är de primitiva gittervektorerna inte ortogonala. Men i dessa fall definieras Miller-indexen konventionellt i förhållande till gittervektorerna för den kubiska supercellen och är därför återigen helt enkelt de kartesiska riktningarna .

Interplanar avstånd

Avståndet d mellan intilliggande ( hkℓ ) gitterplan ges av:

• Kubik:

  ${\frac {1}{d^{2}}}={\frac {h^{2}+k^{2}+ \ell ^{2}}{a^{2}}}$

• Tetragonal:

  ${\frac {1}{d^{2}}}={\frac {h^{2}+k^{2 }}{a^{2}}}+{\frac {\ell ^{2}}{c^{2}}}$

• Hexagonal:

  ${\frac {1}{d^{2}}}={\frac {4}{ 3}}\left({\frac {h^{2}+hk+k^{2}}{a^{2}}}\right)+{\frac {\ell ^{2}}{c^ {2}}}$

• Romboedral:

  ${\frac {1}{d^{2}}}={\frac {(h^{2}+k^{2}+\ell ^{2} )\sin ^{2}\alpha +2(hk+k\ell +h\ell )(\cos ^{2}\alpha -\cos \alpha )}{a^{2}(1-3\cos ^{2}\alpha +2\cos ^{3}\alpha )}}$

• Ortorhombisk:

  ${\frac {1}{d^{2}}}={\frac {h^{2}}{a ^{2}}}+{\frac {k^{2}}{b^{2}}}+{\frac {\ell ^{2}}{c^{2}}}$

• Monoklin:

  ${\frac {1}{d ^{2}}}=\left({\frac {h^{2}}{a^{2}}}+{\frac {k^{2}\sin ^{2}\beta }{b^ {2}}}+{\frac {\ell ^{2}}{c^{2}}}-{\frac {2h\ell \cos \beta }{ac}}\right)\csc ^{2 }\beta$

• ${\frac {1}{d^{2}}}={\frac {{\frac {h^{2}}{a^{2 }}}\sin ^{2}\alpha +{\frac {k^{2}}{b^{2}}}\sin ^{2}\beta +{\frac {\ell ^{2}} {c^{2}}}\sin ^{2}\gamma +{\frac {2k\ell }{bc}}(\cos \beta \cos \gamma -\cos \alpha )+{\frac {2h \ell }{ac}}(\cos \gamma \cos \alpha -\cos \beta )+{\frac {2hk}{ab}}(\cos \alpha \cos \beta -\cos \gamma )}{ 1-\cos ^{2}\alpha -\cos ^{2}\beta -\cos ^{2}\gamma +2\cos \alpha \cos \beta \cos \gamma }}$

  :

Klassificering efter symmetri

Huvudartikel: Kristallsystem

Den definierande egenskapen hos en kristall är dess inneboende symmetri. Att utföra vissa symmetrioperationer på kristallgittret lämnar det oförändrat. Alla kristaller har translationssymmetri i tre riktningar, men vissa har andra symmetrielement också. Till exempel kan rotation av kristallen 180° kring en viss axel resultera i en atomkonfiguration som är identisk med den ursprungliga konfigurationen; kristallen har dubbel rotationssymmetri kring denna axel. Förutom rotationssymmetri kan en kristall ha symmetri i form av spegelplan, och även de så kallade sammansatta symmetrierna, som är en kombination av translation och rotation eller spegelsymmetri. En fullständig klassificering av en kristall uppnås när alla inneboende symmetrier i kristallen identifieras.

Gittersystem

Gittersystem är en gruppering av kristallstrukturer enligt det axiella system som används för att beskriva deras gitter. Varje gittersystem består av en uppsättning av tre axlar i ett speciellt geometriskt arrangemang. Alla kristaller faller in i ett av sju gittersystem. De liknar, men inte riktigt samma som de sju kristallsystemen .

Crystal familj	Gallersystem	Punktgrupp ( Schönflies notation )	14 Bravais galler
			Primitiv (P)	Bascentrerad (S)	Kroppscentrerad (I)	Ansiktscentrerad (F)
Triclinic (a)		C i	aP
Monoklinisk (m)		C 2h	mP	Fröken
Ortorhombisk (o)		D 2h	oP	oS	oI	av
Tetragonal (t)		D 4h	tP		tI
Hexagonal (h)	Rhombohedral	D 3d	hR
	Hexagonal	D 6h	hP
Kubik (c)		O h	cP		cI	cF

Det enklaste och mest symmetriska, det kubiska eller isometriska systemet, har en kubs symmetri, det vill säga den uppvisar fyra trefaldiga rotationsaxlar orienterade vid 109,5° (den tetraedriska vinkeln ) i förhållande till varandra. Dessa trefaldiga axlar ligger längs kubens kroppsdiagonaler. De andra sex gittersystemen, är hexagonala , tetragonala , rhombohedral (ofta förväxlade med det trigonala kristallsystemet ), ortorhombic , monoclinic och triclinic .

Bravais galler

Bravais gitter , även kallade rymdgitter , beskriver det geometriska arrangemanget av gitterpunkterna och därför kristallens translationssymmetri. De tre dimensionerna av rymden ger 14 distinkta Bravais-gitter som beskriver translationssymmetrin. Alla kristallina material som känns igen idag, inte inklusive kvasikristaller , passar i ett av dessa arrangemang. De fjorton tredimensionella gittren, klassificerade efter gittersystem, visas ovan.

Kristallstrukturen består av samma grupp av atomer, basen , placerad runt varje gitterpunkt. Denna grupp av atomer upprepas därför i oändlighet i tre dimensioner enligt arrangemanget av ett av Bravais-gittren. Enhetscellens karakteristiska rotations- och spegelsymmetri beskrivs av dess kristallografiska punktgrupp .

Kristallsystem

Se även: Kristallografisk punktgrupp § Isomorfismer

Ett kristallsystem är en uppsättning punktgrupper där själva punktgrupperna och deras motsvarande rymdgrupper är tilldelade ett gittersystem. Av de 32 punktgrupper som finns i tre dimensioner är de flesta tilldelade endast ett gittersystem, i vilket fall kristallsystemet och gittersystemet båda har samma namn. Fem punktgrupper tilldelas dock två gittersystem, romboedriska och hexagonala, eftersom båda gittersystemen uppvisar trefaldig rotationssymmetri. Dessa punktgrupper tilldelas det trigonala kristallsystemet.

Crystal familj	Kristallsystem	Poänggrupp / Kristallklass	Schönflies	Punktsymmetri	Beställa	Abstrakt grupp
triklinik		pedal	C 1	enantiomorf polär	1	trivial $\mathbb {Z} _{1}$
		pinacoidal	Ci ( S2 ) _	centrosymmetrisk	2	cyklisk $\mathbb {Z} _{2}$
monoklinisk		sphenoidal	C 2	enantiomorf polär	2	cyklisk $\mathbb {Z} _{2}$
		domatisk	Cs ( C1h ) _	polär	2	cyklisk $\mathbb {Z} _{2}$
		prismatisk	C 2h	centrosymmetrisk	4	Klein fyra $\mathbb {V} =\mathbb {Z} _{2}\times \mathbb {Z} _{2}$
ortorombisk		rombisk-disfenoidal	D 2 (V)	enantiomorf	4	Klein fyra $\mathbb {V} =\mathbb {Z} _{2}\times \mathbb {Z} _{2}$
		rombisk- pyramidal	C 2v	polär	4	Klein fyra $\mathbb {V} =\mathbb {Z} _{2}\times \mathbb {Z} _{2}$
		rombisk- dipyramidal	D 2h (V h )	centrosymmetrisk	8	$\mathbb {V} \times \mathbb {Z} _{2}$
tetragonal		tetragonal-pyramidal	C 4	enantiomorf polär	4	cyklisk $\mathbb {Z} _{4}$
		tetragonal-disfenoidal	S 4	icke-centrosymmetrisk	4	cyklisk $\mathbb {Z} _{4}$
		tetragonal-dipyramidal	C 4h	centrosymmetrisk	8	$\mathbb {Z} _{4}\times \mathbb {Z} _{2}$
		tetragonal-trapesoedrisk	D 4	enantiomorf	8	dihedral $\mathbb {D} _{8}=\mathbb {Z} _{4}\rtimes \mathbb {Z} _{2}$
		ditetragonal-pyramidal	C 4v	polär	8	dihedral $\mathbb {D} _{8}=\mathbb {Z} _{4}\rtimes \mathbb {Z} _{2}$
		tetragonal-scalenohedral	D 2d (V d )	icke-centrosymmetrisk	8	dihedral $\mathbb {D} _{8}=\mathbb {Z} _{4}\rtimes \mathbb {Z} _{2}$
		ditetragonal-dipyramidal	D 4h	centrosymmetrisk	16	$\mathbb {D} _{8}\times \mathbb {Z} _{2}$
hexagonal	trigonal	trigonal-pyramidal	C 3	enantiomorf polär	3	cyklisk $\mathbb {Z} _{3}$
		romboedrisk	C3i ( S6 ) _	centrosymmetrisk	6	cyklisk $\mathbb {Z} _{6}=\mathbb {Z} _{3}\times \mathbb {Z} _{2}$
		trigonal-trapesoedrisk	D 3	enantiomorf	6	dihedral $\mathbb {D} _{6}=\mathbb {Z} _{3}\rtimes \mathbb {Z} _{2}$
		ditrigonal-pyramidal	C 3v	polär	6	dihedral $\mathbb {D} _{6}=\mathbb {Z} _{3}\rtimes \mathbb {Z} _{2}$
		ditrigonal-scalenohedral	D 3d	centrosymmetrisk	12	dihedral $\mathbb {D} _{12}=\mathbb {Z} _{6}\rtimes \mathbb {Z} _{2}$
	hexagonal	hexagonal-pyramidal	C 6	enantiomorf polär	6	cyklisk $\mathbb {Z} _{6}=\mathbb {Z} _{3}\times \mathbb {Z} _{2}$
		trigonal-dipyramidal	C 3h	icke-centrosymmetrisk	6	cyklisk $\mathbb {Z} _{6}=\mathbb {Z} _{3}\times \mathbb {Z} _{2}$
		hexagonal-dipyramidal	C 6h	centrosymmetrisk	12	$\mathbb {Z} _{6}\times \mathbb {Z} _{2}$
		hexagonal-trapesoedrisk	D 6	enantiomorf	12	dihedral $\mathbb {D} _{12}=\mathbb {Z} _{6}\rtimes \mathbb {Z} _{2}$
		dihexagonal-pyramidal	C 6v	polär	12	dihedral $\mathbb {D} _{12}=\mathbb {Z} _{6}\rtimes \mathbb {Z} _{2}$
		ditrigonal-dipyramidal	D 3h	icke-centrosymmetrisk	12	dihedral $\mathbb {D} _{12}=\mathbb {Z} _{6}\rtimes \mathbb {Z} _{2}$
		dihexagonal-dipyramidal	D 6h	centrosymmetrisk	24	$\mathbb {D} _{12}\times \mathbb {Z} _{2}$
kubisk		tetartoidal	T	enantiomorf	12	alternerande $\mathbb {A} _{4}$
		diploidal	T h	centrosymmetrisk	24	$\mathbb {A} _{4}\times \mathbb {Z} _{2}$
		gyroidal	O	enantiomorf	24	symmetrisk $\mathbb {S} _{4}$
		hextetraedrisk	T d	icke-centrosymmetrisk	24	symmetrisk $\mathbb {S} _{4}$
		hexoktaedrisk	O h	centrosymmetrisk	48	$\mathbb {S} _{4}\times \mathbb {Z} _{2}$

Totalt finns det sju kristallsystem: trikliniska, monokliniska, ortorombiska, tetragonala, trigonala, hexagonala och kubiska.

Punktgrupper

Den kristallografiska punktgruppen eller kristallklassen är den matematiska gruppen som innefattar symmetrioperationerna som lämnar åtminstone en punkt orörlig och som lämnar utseendet på kristallstrukturen oförändrad. Dessa symmetrioperationer inkluderar

• Reflektion , som reflekterar strukturen över ett reflektionsplan
• Rotation , som roterar strukturen en specificerad del av en cirkel kring en rotationsaxel
• Inversion , som ändrar tecknet för koordinaten för varje punkt med avseende på ett symmetricentrum eller inversionspunkt
• Felaktig rotation , som består av en rotation kring en axel följt av en inversion.

Rotationsaxlar (korrekt och felaktig), reflektionsplan och symmetricentrum kallas tillsammans för symmetrielement . Det finns 32 möjliga kristallklasser. Var och en kan klassificeras i ett av de sju kristallsystemen.

Rymdgrupper

Förutom operationerna för punktgruppen innehåller rymdgruppen för kristallstrukturen translationella symmetrioperationer. Dessa inkluderar:

• Rena översättningar , som flyttar en punkt längs en vektor
• Skruvaxlar , som roterar en punkt runt en axel samtidigt som de förflyttas parallellt med axeln.
• Glidplan , som reflekterar en punkt genom ett plan samtidigt som den förflyttas parallellt med planet.

Det finns 230 distinkta rymdgrupper.

Atomisk koordination

Genom att överväga arrangemanget av atomer i förhållande till varandra, deras koordinationsnummer, interatomära avstånd, typer av bindning etc., är det möjligt att bilda sig en allmän bild av strukturerna och alternativa sätt att visualisera dem.

Stäng packning

Huvudartikel: Närpackning av lika sfärer

hcp gitter (vänster) och fcc gitter (höger)

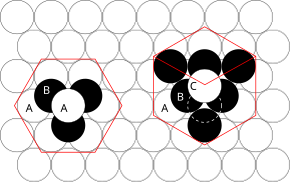
De involverade principerna kan förstås genom att överväga det mest effektiva sättet att packa ihop lika stora sfärer och stapla tätpackade atomplan i tre dimensioner. Till exempel, om plan A ligger under plan B, finns det två möjliga sätt att placera en extra atom ovanpå lager B. Om ett ytterligare lager placerades direkt över plan A skulle detta ge upphov till följande serie:

... ABABABAB ...

Detta arrangemang av atomer i en kristallstruktur är känt som hexagonal close packing (hcp) .

Om dock alla tre plan är förskjutna i förhållande till varandra och det inte är förrän det fjärde lagret är placerat direkt över plan A som sekvensen upprepas, så uppstår följande sekvens:

... ABCABCABC ...

Denna typ av strukturellt arrangemang är känt som cubic close packing (ccp) .

Enhetscellen i ett ccp-arrangemang av atomer är den ansiktscentrerade kubiska (fcc) enhetscellen. Detta är inte omedelbart uppenbart eftersom de tätt packade lagren är parallella med {111}-planen i fcc-enhetscellen. Det finns fyra olika orienteringar av de tätpackade lagren.

APF och CN

Huvudartiklar: Atomisk packningsfaktor och koordinationsnummer

En viktig egenskap hos en kristallin struktur är dess atomära packningsfaktor (APF). Detta beräknas genom att anta att alla atomer är identiska sfärer, med en radie som är tillräckligt stor för att varje sfär anligger mot nästa. Atompackningsfaktorn är andelen utrymme som fylls av dessa sfärer som kan räknas ut genom att beräkna sfärernas totala volym och dividera med cellens volym enligt följande:

$\mathrm {APF} ={\frac {N_{\mathrm {partikel} }V_{\mathrm {partikel} }}{V_{\text{enhetscell}}}}$

En annan viktig egenskap hos en kristallin struktur är dess koordinationsnummer (CN). Detta är antalet närmaste grannar till en central atom i strukturen.

APF och CN för de vanligaste kristallstrukturerna visas nedan:

Kristallstruktur	Atomisk packningsfaktor	Koordinationsnummer ( Geometri )
Diamant kubisk	0,34	4 ( Tetraeder )
Enkel kubisk	0,52	6 ( Octahedron )
Kroppscentrerad kubik (BCC)	0,68	8 ( kub )
Ansiktscentrerad kubik (FCC)	0,74	12 ( Cuboctahedron )
Hexagonal close-packed (HCP)	0,74	12 ( triangulär ortobikupa )

Packningseffektiviteten på 74 % för FCC och HCP är den maximala densiteten som är möjlig i enhetsceller konstruerade av sfärer av endast en storlek.

Mellansideswebbplatser

Huvudartikel: Mellansideswebbplats

Oktaedriska (röda) och tetraedriska (blå) mellanliggande platser i ett ansiktscentrerat kubiskt gitter.

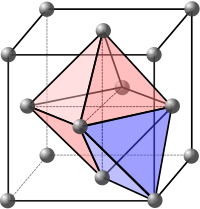
Interstitiella platser hänvisar till de tomma utrymmena mellan atomerna i kristallgittret. Dessa utrymmen kan fyllas av motsatt laddade joner för att bilda strukturer med flera element. De kan också fyllas av föroreningsatomer eller självinterstitialer för att bilda interstitiella defekter .

Defekter och föroreningar

Huvudartikel: Kristallografisk defekt

Riktiga kristaller har defekter eller oregelbundenheter i de idealiska arrangemangen som beskrivs ovan och det är dessa defekter som kritiskt bestämmer många av de elektriska och mekaniska egenskaperna hos verkliga material.

Föroreningar

När en atom ersätter en av de huvudsakliga atomkomponenterna i kristallstrukturen, kan förändringar i materialets elektriska och termiska egenskaper uppstå. Föroreningar kan också visa sig som elektronspinnföroreningar i vissa material. Forskning på magnetiska föroreningar visar att avsevärda förändringar av vissa egenskaper som specifik värme kan påverkas av små koncentrationer av en förorening, eftersom till exempel föroreningar i halvledande ferromagnetiska legeringar kan leda till olika egenskaper som först förutspåddes i slutet av 1960-talet.

Dislokationer

Huvudartikel: Dislokation

Dislokationer i ett kristallgitter är linjedefekter som är associerade med lokala spänningsfält. Dislokationer tillåter skjuvning vid lägre spänning än vad som behövs för en perfekt kristallstruktur. De lokala spänningsfälten resulterar i interaktioner mellan dislokationerna som sedan resulterar i töjningshärdning eller kallbearbetning .

Korngränser

Huvudartikel: Korngräns

Korngränser är gränssnitt där kristaller med olika orienteringar möts. En korngräns är ett enfasgränssnitt, med kristaller på varje sida av gränsen identiska utom i orientering. Termen "kristallitgräns" används ibland, men sällan. Korngränsområden innehåller de atomer som har störts från sina ursprungliga gitterplatser, dislokationer och föroreningar som har migrerat till den lägre energikorngränsen.

Genom att behandla en korngräns geometriskt som ett gränssnitt mellan en enkristall som skärs i två delar, varav den ena är roterad, ser vi att det krävs fem variabler för att definiera en korngräns. De två första talen kommer från enhetsvektorn som anger en rotationsaxel. Den tredje siffran anger kornens rotationsvinkel. De två sista siffrorna anger korngränsens plan (eller en enhetsvektor som är normal mot detta plan).

Korngränser stör rörelsen av dislokationer genom ett material, så att minska kristallitstorleken är ett vanligt sätt att förbättra styrkan, som beskrivs av Hall- Petch- relationen. Eftersom korngränser är defekter i kristallstrukturen tenderar de att minska materialets elektriska och termiska ledningsförmåga . Den höga gränsytenergin och relativt svaga bindningen i de flesta korngränser gör dem ofta till föredragna platser för uppkomsten av korrosion och för utfällning av nya faser från det fasta ämnet. De är också viktiga för många av krypningsmekanismerna .

Korngränser är i allmänhet bara några nanometer breda. I vanliga material är kristalliter tillräckligt stora för att korngränser står för en liten del av materialet. Men mycket små kornstorlekar är möjliga. I nanokristallina fasta ämnen blir korngränser en betydande volymfraktion av materialet, med djupgående effekter på sådana egenskaper som diffusion och plasticitet . I gränsen för små kristalliter, när volymfraktionen av korngränserna närmar sig 100 %, upphör materialet att ha någon kristallin karaktär och blir därmed ett amorft fast ämne .

Förutsägelse av struktur

Huvudartikel: Kristallstrukturförutsägelse

Svårigheten att förutsäga stabila kristallstrukturer baserat på kunskapen om enbart den kemiska sammansättningen har länge varit en stötesten på vägen mot helt beräkningsmässig materialdesign. Nu, med kraftfullare algoritmer och högpresterande beräkningar, kan strukturer av medelhög komplexitet förutsägas med hjälp av sådana tillvägagångssätt som evolutionära algoritmer , slumpmässigt urval eller metadynamik.

Kristallstrukturerna för enkla joniska fasta ämnen (t.ex. NaCl eller bordssalt) har länge rationaliserats i termer av Paulings regler , som först sattes upp 1929 av Linus Pauling , som av många sedan hänvisades till som "den kemiska bindningens fader". Pauling övervägde också arten av de interatomiska krafterna i metaller och drog slutsatsen att ungefär hälften av de fem d-orbitalerna i övergångsmetallerna är involverade i bindning, med de återstående icke-bindande d-orbitalerna som ansvarar för de magnetiska egenskaperna. Pauling kunde därför korrelera antalet d-orbitaler i bindningsbildning med bindningslängden, såväl som med många av ämnets fysikaliska egenskaper. Han introducerade därefter den metalliska orbitalen, en extra orbital som är nödvändig för att tillåta ohämmad resonans av valensbindningar mellan olika elektroniska strukturer.

I teorin om resonansvalensbindning kretsar de faktorer som bestämmer valet av en bland alternativa kristallstrukturer av en metall eller intermetallisk förening kring resonansenergin för bindningar mellan interatomära positioner. Det är tydligt att vissa resonanssätt skulle ge större bidrag (vara mer mekaniskt stabila än andra), och att i synnerhet ett enkelt förhållande mellan antal obligationer och antal positioner skulle vara exceptionellt. Den resulterande principen är att en speciell stabilitet är förknippad med de enklaste förhållandena eller "bindningstalen": 1 ⁄ 2 , 1 ⁄ 3 , 2 ⁄ 3 , 1 ⁄ 4 , 3 ⁄ 4 , etc. Valet av struktur och värdet av det axiella förhållandet (som bestämmer de relativa bindningslängderna) är alltså ett resultat av en atoms ansträngning att använda sin valens vid bildandet av stabila bindningar med enkla bråkbindningstal.

Efter att ha postulerat en direkt korrelation mellan elektronkoncentration och kristallstruktur i beta-faslegeringar, analyserade Hume-Rothery trenderna i smältpunkter, kompressibiliteter och bindningslängder som en funktion av gruppnummer i det periodiska systemet för att etablera ett system av valenser av övergångselementen i metalliskt tillstånd. Denna behandling betonade således den ökande bindningsstyrkan som en funktion av gruppantal. Riktningskrafternas funktion betonades i en artikel om förhållandet mellan bindningshybrider och de metalliska strukturerna. Den resulterande korrelationen mellan elektroniska och kristallina strukturer sammanfattas av en enda parameter, vikten av d-elektronerna per hybridiserad metallisk orbital. "D-vikten" beräknas till 0,5, 0,7 och 0,9 för strukturerna fcc, hcp och bcc. Förhållandet mellan d-elektroner och kristallstruktur blir därmed uppenbart.

I kristallstrukturförutsägelser/simuleringar tillämpas vanligtvis periodiciteten, eftersom systemet föreställs vara obegränsat i alla riktningar. Med utgångspunkt från en triklinisk struktur utan ytterligare symmetriegenskaper kan systemet drivas att visa ytterligare symmetriegenskaper genom att tillämpa Newtons andra lag om partiklar i enhetscellen och en nyligen utvecklad dynamisk ekvation för systemperiodvektorerna (gitterparametrar inklusive vinklar ), även om systemet utsätts för yttre påfrestningar.

Polymorfism

Kvarts är en av flera kristallina former av kiseldioxid , SiO ₂ . De viktigaste formerna av kiseldioxid inkluderar: α-kvarts , β-kvarts , tridymit , cristobalit , coesite och stishovite .

Polymorfism är förekomsten av flera kristallina former av ett material. Det finns i många kristallina material inklusive polymerer , mineraler och metaller . Enligt Gibbs regler för fasjämvikt är dessa unika kristallina faser beroende av intensiva variabler som tryck och temperatur. Polymorfism är relaterad till allotropi , som hänvisar till elementära fasta ämnen . Den fullständiga morfologin av ett material beskrivs av polymorfism och andra variabler såsom kristallvana , amorf fraktion eller kristallografiska defekter . Polymorfer har olika stabilitet och kan spontant och irreversibelt transformeras från en metastabil form (eller termodynamiskt instabil form) till den stabila formen vid en viss temperatur. De uppvisar också olika smältpunkter , lösligheter och röntgendiffraktionsmönster .

Ett bra exempel på detta är kvartsformen av kiseldioxid eller SiO ₂ . I de allra flesta silikater uppvisar Si-atomen tetraedrisk koordination med 4 syreämnen. Alla utom en av de kristallina formerna involverar tetraedriska {SiO ₄ } enheter sammanlänkade av delade hörn i olika arrangemang. I olika mineraler uppvisar tetraedrarna olika grader av nätverksbildning och polymerisation. Till exempel förekommer de ensamma, sammanfogade i par, i större ändliga kluster inklusive ringar, i kedjor, dubbla kedjor, ark och tredimensionella ramverk. Mineralerna klassificeras i grupper utifrån dessa strukturer. , delas endast 2 av 4 av varje kanterna på {SiO _{4 }-tetraedrarna med andra, vilket ger den kemiska nettoformeln för kiseldioxid: SiO 2} .

Ett annat exempel är elementärt tenn (Sn), som är formbart nära omgivningstemperaturer men är skört när det kyls. Denna förändring i mekaniska egenskaper på grund av existensen av dess två stora allotroper , α- och β-tenn. De två allotroperna som påträffas vid normalt tryck och temperatur, α-tenn och β-tenn, är mer kända som grått tenn respektive vitt tenn . Ytterligare två allotroper, γ och σ, finns vid temperaturer över 161 °C och tryck över flera GPa. Vitt tenn är metalliskt och är den stabila kristallina formen vid eller över rumstemperatur. Under 13,2 °C finns tenn i grå form, som har en diamantkubisk kristallstruktur, liknande diamant , kisel eller germanium . Grått tenn har inga metalliska egenskaper alls, är ett matt grått pulverformigt material och har få användningsområden, förutom ett fåtal specialiserade halvledarapplikationer . Även om α–β-omvandlingstemperaturen för tenn nominellt är 13,2 °C, sänker föroreningar (t.ex. Al, Zn, etc.) övergångstemperaturen väl under 0 °C, och vid tillsats av Sb eller Bi kanske omvandlingen inte inträffar alls.

Fysikaliska egenskaper

Tjugo av de 32 kristallklasserna är piezoelektriska , och kristaller som tillhör en av dessa klasser (punktgrupper) visar piezoelektricitet . Alla piezoelektriska klasser saknar inversionssymmetri . Vilket material som helst utvecklar en dielektrisk polarisation när ett elektriskt fält appliceras, men ett ämne som har en sådan naturlig laddningsseparation även i frånvaro av ett fält kallas ett polärt material. Huruvida ett material är polärt eller inte bestäms enbart av dess kristallstruktur. Endast 10 av de 32 punktgrupperna är polära . Alla polära kristaller är pyroelektriska , så de 10 polära kristallklasserna kallas ibland för de pyroelektriska klasserna.

Det finns några få kristallstrukturer, särskilt perovskitstrukturen , som uppvisar ferroelektriskt beteende. Detta är analogt med ferromagnetism , i det att i frånvaro av ett elektriskt fält under produktionen, uppvisar den ferroelektriska kristallen ingen polarisation. Vid applicering av ett elektriskt fält av tillräcklig storlek blir kristallen permanent polariserad. Denna polarisation kan vändas med en tillräckligt stor motladdning, på samma sätt som en ferromagnet kan vändas. Men även om de kallas ferroelektriska, beror effekten på kristallstrukturen (inte närvaron av en järnmetall).

Se även

För mer detaljerad information om specifika tekniska tillämpningar, se Materialvetenskap , Keramisk ingenjörskonst , Metallurgi och Lista över biofysiskt viktiga makromolekylära kristallstrukturer .

• Brillouin-zon – Primitiv cell i det reciproka rymdgittret av kristaller
• Kristallteknik
• Kristalltillväxt – Huvudstadiet i en kristalliseringsprocess
• Kristallografisk databas
• Bråkkoordinater
• Frank–Kasper faser
• Hermann–Mauguin notation – Notation för att representera symmetri i punktgrupper, plangrupper och rymdgrupper
• Laseruppvärmd piedestaltillväxt – kristalltillväxtteknik Sidor som visar wikidata-beskrivningar som reserv
• Flytande kristall – Materiens tillstånd med egenskaper hos både konventionella vätskor och kristaller
• Patterson-funktion – röntgenkristallografi Sidor som visar wikidata-beskrivningar som en reserv
• Periodiska systemet (kristallstruktur) – (för grundämnen som är fasta vid standardtemperatur och standardtryck) ger den kristallina strukturen av den eller de mest termodynamiskt stabila formerna under dessa förhållanden. I alla andra fall är den angivna strukturen för elementet vid dess smältpunkt Sidor som visar wikidata-beskrivningar som en reserv
• Primitiv cell – Upprepande enhet som bildas av vektorerna som spänner över punkterna i ett gitter Sidor som visar korta beskrivningar av omdirigeringsmål
• Frökristall – Liten bit av en enkristall som används för att initiera tillväxt av en större kristall
• Wigner–Seitz-cell – Primitiv cell av kristallgitter med Voronoi-nedbrytning tillämpad

externa länkar

Media relaterade till Kristallstrukturer på Wikimedia Commons

• Kristallernas inre struktur... Kristallografi för nybörjare
• Olika typer av kristallstruktur
• Bilaga A från manualen för Atoms, programvara för XAFS
• Introduktion till mineraler: Kristallklass och system
• Introduktion till kristallografi och mineralkristallsystem
• Kristallplan och Miller-index
• Interaktiva 3D-kristallmodeller
• Specifika Crystal 3D-modeller
• Kristallografi öppen databas (med mer än 140 000 kristallstrukturer)