Dielektrisk

Ej att förväxla med dielektrisk konstant eller dialektik .

Ett polariserat dielektriskt material

Inom elektromagnetism är ett dielektriskt (eller dielektriskt medium ) en elektrisk isolator som kan polariseras av ett applicerat elektriskt fält . När ett dielektriskt material placeras i ett elektriskt fält, elektriska laddningar genom materialet som de gör i en elektrisk ledare , eftersom de inte har några löst bundna, eller fria, elektroner som kan driva genom materialet, utan istället skiftar de, endast något, från deras genomsnittliga jämviktspositioner, vilket orsakar dielektrisk polarisering . På grund av dielektrisk polarisation förskjuts positiva laddningar i fältets riktning och negativa laddningar förskjuts i motsatt riktning mot fältet (till exempel, om fältet rör sig parallellt med den positiva x-axeln, kommer de negativa laddningarna att förskjutas i den negativa riktningen x -riktning). Detta skapar ett internt elektriskt fält som minskar det totala fältet inom själva dielektriken. Om ett dielektrikum är sammansatt av svagt bundna molekyler blir dessa molekyler inte bara polariserade, utan omorienteras också så att deras symmetriaxlar är i linje med fältet.

Studiet av dielektriska egenskaper handlar om lagring och spridning av elektrisk och magnetisk energi i material. Dielektrikum är viktiga för att förklara olika fenomen inom elektronik , optik , fast tillståndsfysik och cellbiofysik .

Terminologi

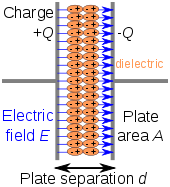
Även om termen isolator antyder låg elektrisk ledning , betyder dielektrisk vanligtvis material med hög polariserbarhet . Det senare uttrycks av ett tal som kallas relativ permittivitet . Termen isolator används vanligtvis för att indikera elektriskt hinder medan termen dielektrikum används för att indikera materialets energilagringskapacitet (med hjälp av polarisation) . Ett vanligt exempel på ett dielektrikum är det elektriskt isolerande materialet mellan metallplattorna i en kondensator . Polariseringen av dielektrikumet av det pålagda elektriska fältet ökar kondensatorns ytladdning för den givna elektriska fältstyrkan.

Termen dielektrisk myntades av William Whewell (från dia + elektrisk ) som svar på en begäran från Michael Faraday . Ett perfekt dielektrikum är ett material med noll elektrisk ledningsförmåga ( jfr perfekt ledare oändlig elektrisk ledningsförmåga), vilket således endast uppvisar en förskjutningsström ; därför lagrar och returnerar den elektrisk energi som om den vore en idealisk kondensator.

Elektrisk känslighet

Huvudartiklar: Elektrisk susceptibilitet och Permittivitet

Den elektriska känsligheten χ _e för ett dielektriskt material är ett mått på hur lätt det polariserar som svar på ett elektriskt fält. Detta bestämmer i sin tur materialets elektriska permittivitet och påverkar således många andra fenomen i det mediet, från kondensatorernas kapacitans till ljusets hastighet .

Den definieras som proportionalitetskonstanten (som kan vara en tensor ) som relaterar ett elektriskt fält E till den inducerade dielektriska polarisationsdensiteten P så att

$$\mathbf {P} =\varepsilon _{0}\chi _{e}\mathbf {E} ,$$

₀ där ε är den elektriska permittiviteten för ledigt utrymme .

mediums känslighet är relaterad till dess relativa permittivitet εr _by

$$\chi _{e}\ =\varepsilon _{r}-1.$$

Så i fallet med ett vakuum,

$$\chi _{e}\ =0.$$

Den elektriska förskjutningen D är relaterad till polarisationsdensiteten P by

$$\mathbf {D} \ =\ \varepsilon _{0}\mathbf {E} +\mathbf {P} \ =\ \varepsilon _{0}\left(1+\chi _{e}\right )\mathbf {E} \ =\ \varepsilon _{0}\varepsilon _{r}\mathbf {E} .$$

Spridning och kausalitet

I allmänhet kan ett material inte polarisera omedelbart som svar på ett applicerat fält. Den mer allmänna formuleringen som en funktion av tiden är

$$\mathbf {P} (t)=\varepsilon _{0}\int _{-\infty }^{t}\chi _{e}\left(tt'\right)\mathbf {E} ( t')\,dt'.$$

Det vill säga, polarisationen är en faltning av det elektriska fältet vid tidigare tidpunkter med tidsberoende susceptibilitet given av χ _e (Δ t ). Den övre gränsen för denna integral kan också utökas till oändligheten om man definierar χ _e (Δ t ) = 0 för Δ t < 0 . Ett momentant svar motsvarar Dirac deltafunktionskänslighet χ _e Δ t ) = χ _e δ (Δ t . ( )

Det är bekvämare i ett linjärt system att ta Fouriertransformen och skriva detta förhållande som en funktion av frekvensen. På grund av faltningssatsen blir integralen en enkel produkt,

$$\mathbf {P} (\omega )=\varepsilon _{0}\chi _{e}(\omega )\mathbf {E} (\omega ).$$

Känsligheten (eller motsvarande permittiviteten) är frekvensberoende. Förändringen av känslighet med avseende på frekvens kännetecknar materialets dispersionsegenskaper .

Dessutom, det faktum att polariseringen endast kan bero på det elektriska fältet vid tidigare tidpunkter (dvs. χ _e (Δ t ) = 0 för Δ t < 0 ), en konsekvens av kausalitet , ålägger Kramers-Kronig begränsningar för det verkliga och imaginära delar av känsligheten χ _e ( ω ).

Dielektrisk polarisation

Grundläggande atommodell

Elektriskt fältinteraktion med en atom enligt den klassiska dielektriska modellen

I det klassiska förhållningssättet till dielektrikumet består materialet av atomer. Varje atom består av ett moln av negativ laddning (elektroner) bundna till och som omger en positiv punktladdning i dess centrum. I närvaro av ett elektriskt fält förvrängs laddningsmolnet, som visas uppe till höger i figuren.

Detta kan reduceras till en enkel dipol med hjälp av superpositionsprincipen . En dipol kännetecknas av dess dipolmoment , en vektorkvantitet som visas i figuren som den blå pilen märkt M. Det är förhållandet mellan det elektriska fältet och dipolmomentet som ger upphov till dielektrikets beteende. (Observera att dipolmomentet pekar i samma riktning som det elektriska fältet i figuren. Detta är inte alltid fallet, och är en stor förenkling, men är sant för många material.)

När det elektriska fältet avlägsnas återgår atomen till sitt ursprungliga tillstånd. Den tid som krävs för att göra det kallas avkopplingstid ; ett exponentiellt förfall.

Detta är kärnan i modellen i fysik. Dielektrikens beteende beror nu på situationen. Ju mer komplicerad situationen är, desto rikare måste modellen vara för att korrekt beskriva beteendet. Viktiga frågor är:

• Är det elektriska fältet konstant eller varierar det med tiden? I vilken takt?
• Beror svaret på riktningen för det applicerade fältet ( materialets isotropi )?
• Är svaret detsamma överallt ( homogenitet i materialet)?
• Måste man ta hänsyn till några gränser eller gränssnitt?
• Är svaret linjärt med avseende på fältet, eller finns det olinjäriteter ?

Förhållandet mellan det elektriska fältet E och dipolmomentet M ger upphov till beteendet hos dielektrikumet, som för ett givet material kan karakteriseras av funktionen F definierad av ekvationen:

$$\mathbf {M} =\mathbf {F} (\mathbf {E} ).$$

När både typen av elektriskt fält och typen av material har definierats, väljer man sedan den enklaste funktionen F som korrekt förutsäger de intressanta fenomenen. Exempel på fenomen som kan modelleras på detta sätt är:

• Brytningsindex
• Grupphastighetsspridning
• Dubbelbrytning
• Självfokuserande
• Harmonisk generering

Dipolär polarisering

Dipolär polarisation är en polarisation som antingen är inneboende i polära molekyler (orienteringspolarisation), eller kan induceras i vilken molekyl som helst där den asymmetriska distorsionen av kärnorna är möjlig (distorsionspolarisation). Orienteringspolarisering är resultatet av en permanent dipol, t.ex. den som uppstår från 104,45° vinkeln mellan de asymmetriska bindningarna mellan syre- och väteatomer i vattenmolekylen, som bibehåller polarisering i frånvaro av ett externt elektriskt fält. Sammansättningen av dessa dipoler bildar en makroskopisk polarisation.

När ett externt elektriskt fält appliceras, förblir avståndet mellan laddningar inom varje permanent dipol, vilket är relaterat till kemisk bindning , konstant i orienteringspolarisation; emellertid roterar själva polarisationsriktningen. Denna rotation sker på en tidsskala som beror på vridmomentet och den omgivande lokala viskositeten hos molekylerna. Eftersom rotationen inte är momentan, förlorar dipolära polarisationer svaret på elektriska fält vid de högsta frekvenserna. En molekyl roterar cirka 1 radian per pikosekund i en vätska, så denna förlust inträffar vid cirka 10 ¹¹ Hz (i mikrovågsområdet). Fördröjningen av svaret på förändringen av det elektriska fältet orsakar friktion och värme.

När ett externt elektriskt fält appliceras vid infraröda frekvenser eller lägre, böjs och sträcks molekylerna av fältet och det molekylära dipolmomentet ändras. Den molekylära vibrationsfrekvensen är ungefär det omvända av den tid det tar för molekylerna att böjas, och denna distorsionspolarisation försvinner över det infraröda.

Jonisk polarisering

Jonisk polarisation är polarisering som orsakas av relativa förskjutningar mellan positiva och negativa joner i jonkristaller (till exempel NaCl ).

Om en kristall eller molekyl består av atomer av mer än ett slag, lutar fördelningen av laddningar runt en atom i kristallen eller molekylen till positiv eller negativ. Som ett resultat, när gittervibrationer eller molekylära vibrationer inducerar relativa förskjutningar av atomerna, förskjuts också centra för positiva och negativa laddningar. Placeringen av dessa centra påverkas av förskjutningarnas symmetri. När centran inte överensstämmer, uppstår polarisering i molekyler eller kristaller. Denna polarisering kallas jonisk polarisering .

Jonisk polarisering orsakar den ferroelektriska effekten såväl som dipolär polarisation. Den ferroelektriska övergången, som orsakas av orienteringen av permanenta dipoler längs en viss riktning, kallas en ordningsstörningsfasövergång . Övergången som orsakas av joniska polarisationer i kristaller kallas en förskjutande fasövergång .

I celler

Jonisk polarisering möjliggör produktion av energirika föreningar i celler (protonpumpen i mitokondrier ) och, vid plasmamembranet , etablerar vilopotentialen , energetiskt ogynnsam transport av joner och cell-till-cell-kommunikation ( Na+/ K+-ATPas ).

Alla celler i djurkroppsvävnader är elektriskt polariserade – med andra ord upprätthåller de en spänningsskillnad över cellens plasmamembran , känd som membranpotentialen . Denna elektriska polarisering är resultatet av ett komplext samspel mellan jontransportörer och jonkanaler .

I neuroner varierar typerna av jonkanaler i membranet vanligtvis över olika delar av cellen, vilket ger dendriterna, axonet och cellkroppen olika elektriska egenskaper. Som ett resultat kan vissa delar av membranet hos en neuron vara exciterbara (kapabla att generera aktionspotentialer), medan andra inte är det.

Dielektrisk dispersion

Inom fysiken är dielektrisk dispersion beroendet av permittiviteten hos ett dielektriskt material på frekvensen av ett pålagt elektriskt fält. Eftersom det finns en fördröjning mellan förändringar i polarisation och förändringar i det elektriska fältet, är dielektrikets permittivitet en komplex funktion av det elektriska fältets frekvens. Dielektrisk dispersion är mycket viktig för tillämpningar av dielektriska material och analys av polarisationssystem.

Detta är ett exempel på ett allmänt fenomen som kallas materialspridning : ett frekvensberoende svar hos ett medium för vågutbredning.

När frekvensen blir högre:

1. Den dipolära polarisationen kan inte längre följa svängningarna i det elektriska fältet i mikrovågsområdet runt 10 ¹⁰ Hz ,
2. Jonpolarisationen och molekylär distorsion kan inte längre spåra det elektriska fältet förbi det infraröda eller långt infraröda området runt 10 ¹³ Hz,
3. Den elektroniska polarisationen förlorar sin respons i det ultravioletta området runt 10 ¹⁵ Hz.

₀₀ I frekvensområdet ovanför ultraviolett närmar permittiviteten konstanten ε i varje ämne, där ε är permittiviteten för det fria utrymmet. Eftersom permittivitet indikerar styrkan av relationen mellan ett elektriskt fält och polarisation, om en polariseringsprocess förlorar sitt svar, minskar permittiviteten.

Dielektrisk avslappning

Dielektrisk relaxation är den momentana fördröjningen (eller fördröjningen) i den dielektriska konstanten för ett material. Detta orsakas vanligtvis av fördröjningen i molekylär polarisation med avseende på ett förändrat elektriskt fält i ett dielektriskt medium (t.ex. inuti kondensatorer eller mellan två stora ledande ytor). Dielektrisk relaxation i föränderliga elektriska fält kan anses vara analog med hysteres vid föränderliga magnetfält (t.ex. i induktor- eller transformatorkärnor ). Relaxation i allmänhet är en fördröjning eller fördröjning i svaret från ett linjärt system , och därför mäts dielektrisk relaxation i förhållande till de förväntade linjära stationära (jämvikts) dielektriska värdena. Tidsfördröjningen mellan det elektriska fältet och polariseringen innebär en irreversibel nedbrytning av Gibbs fria energi .

Inom fysiken hänvisar dielektrisk avslappning till avslappningssvaret hos ett dielektriskt medium på ett externt, oscillerande elektriskt fält . Denna avslappning beskrivs ofta i termer av permittivitet som en funktion av frekvens , vilket för idealiska system kan beskrivas med Debye-ekvationen. Å andra sidan visar distorsionen relaterad till jonisk och elektronisk polarisation beteende av resonans- eller oscillatortyp . Karaktären av distorsionsprocessen beror på strukturen, sammansättningen och omgivningen av provet.

Debye avkoppling

Debye-relaxation är det dielektriska relaxationssvaret för en idealisk, icke-interagerande population av dipoler på ett alternerande externt elektriskt fält. Det uttrycks vanligtvis i den komplexa permittiviteten ε för ett medium som en funktion av fältets vinkelfrekvens ω :

$${\hat {\varepsilon }}(\omega )=\varepsilon _{\infty }+{\frac {\Delta \varepsilon } {1+i\omega \tau }},$$

där ε _∞ är permittiviteten vid högfrekvensgränsen, − _Δ ε = εs ε ∞ _där ε s _är den statiska lågfrekventa permittiviteten och τ är den karakteristiska relaxationstiden för mediet. Att separera i den reella delen $\varepsilon '$ och den imaginära delen $\varepsilon ''$ av den komplexa dielektriska permittiviteten ger:

$${\displayed 'style}\begin{aligned {\begin{aligned} varepsilon _{\infty }+{\frac {\varepsilon _{s}-\varepsilon _{\infty }}{1+\omega ^{2}\tau ^{2}}}\\[3pt]\varepsilon ''&={\frac {(\varepsilon _{s}-\varepsilon _{\infty })\omega \tau }{1+\omega ^{2}\tau ^{2}}}\end{aligned }}}$$

Observera att ekvationen ovan för ${\hat {\varepsilon }}(\omega )$ ibland skrivs med $1-i\omega \tau$ i nämnaren på grund av en pågående tvetydighet i teckenkonventionen där många källor representerar tidsberoendet för det komplexa elektriska fältet med $\exp(-i\omega t)$ medan andra använder $\exp(+i\omega t)$ . I den tidigare konventionen ges funktionerna $\varepsilon '$ och $\varepsilon ''$ som representerar verkliga och imaginära delar av ${\hat {\varepsilon }}(\omega )=\varepsilon '+i\varepsilon ''$ medan i den senare konventionen ${\hat {\varepsilon } }(\omega )=\varepsilon '-i\varepsilon ''$ . Ovanstående ekvation använder den senare konventionen.

Den dielektriska förlusten representeras också av förlusttangenten:

$$\tan(\delta )={\frac {\varepsilon ''}{\varepsilon ' varepsilon '}}={\frac {\left(\varepsilon _{s}-\varepsilon _{\infty }\right)\omega \tau }{\varepsilon _{s}+\varepsilon _{\infty }\ omega ^{2}\tau ^{2}}}$$

Denna avslappningsmodell introducerades av och uppkallad efter fysikern Peter Debye (1913). Det är karakteristiskt för dynamisk polarisering med endast en relaxationstid.

Varianter av Debye-ekvationen

Cole–Cole-ekvation

Denna ekvation används när den dielektriska förlusttoppen visar symmetrisk breddning.

Cole–Davidsons ekvation

Denna ekvation används när den dielektriska förlusttoppen visar asymmetrisk breddning.

Havriliak–Negami-relaxation

Denna ekvation tar hänsyn till både symmetrisk och asymmetrisk breddning.

Kohlrausch–Williams–Watts funktion

Fouriertransform av sträckt exponentialfunktion .

Curie-von Schweidler lag

Detta visar svaret av dielektrikum på ett applicerat DC-fält för att bete sig enligt en effektlag, som kan uttryckas som en integral över viktade exponentialfunktioner.

Paraelektricitet

Se även: Ferroelektricitet

Paraelektricitet är det nominella beteendet hos dielektrika när den dielektriska permittivitetstensorn är proportionell mot enhetsmatrisen, dvs ett pålagt elektriskt fält orsakar polarisering och/eller inriktning av dipoler endast parallellt med det pålagda elektriska fältet. I motsats till analogin med ett paramagnetiskt material behöver det inte finnas någon permanent elektrisk dipol i ett paraelektriskt material. Borttagning av fälten resulterar i att den dipolära polarisationen återgår till noll. De mekanismer som orsakar paraelektriskt beteende är distorsion av enskilda joner (förskjutning av elektronmolnet från kärnan) och polarisering av molekyler eller kombinationer av joner eller defekter.

Paraelektricitet kan uppstå i kristallfaser där elektriska dipoler är oinriktade och därmed har potential att rikta in sig i ett externt elektriskt fält och försvaga det.

De flesta dielektriska material är paraelektriska. Ett specifikt exempel på ett paraelektriskt material med hög dielektricitetskonstant är strontiumtitanat .

LiNbO3 - _oordnad kristallen är ferroelektrisk under 1430 K och över denna temperatur omvandlas den till en paraelektrisk fas. På liknande sätt uppvisar andra perovskiter också paraelektricitet vid höga temperaturer.

Paraelektricitet har utforskats som en möjlig kylmekanism; polarisering av en paraelektrik genom att applicera ett elektriskt fält under adiabatiska processförhållanden höjer temperaturen, medan borttagning av fältet sänker temperaturen. En värmepump som arbetar genom att polarisera det paraelektriska elementet, vilket låter det återgå till omgivningstemperatur (genom att avleda den extra värmen), föra det i kontakt med föremålet som ska kylas och slutligen depolarisera det, skulle resultera i kylning.

Stämbarhet

Avstämbara dielektrika är isolatorer vars förmåga att lagra elektrisk laddning ändras när en spänning appliceras.

I allmänhet används strontiumtitanat ( SrTiO
_{3 ) för enheter som arbetar vid låga temperaturer, medan} bariumstrontiumtitanat ( Ba
_1−x Sr
_x TiO
₃ ) ersätter rumstemperaturenheter. Andra potentiella material inkluderar mikrovågsdielektrik och kolnanorör (CNT) kompositer.

Under 2013 producerade flerskiktsskikt av strontiumtitanat sammanflätade med enstaka skikt av strontiumoxid ett dielektrikum som kan arbeta vid upp till 125 GHz. Materialet skapades via molekylär strålepitaxi . De två har oöverensstämmande kristallavstånd som ger spänning i strontiumtitanatskiktet som gör det mindre stabilt och avstämbart.

System som Ba
_1−x Sr
_x TiO
₃ har en paraelektrisk–ferroelektrisk övergång strax under omgivningstemperaturen, vilket ger hög avstämningsförmåga. Filmer lider betydande förluster till följd av defekter.

Ansökningar

Kondensatorer

Huvudartikel: Kondensator

Laddningsseparation i en kondensator med parallella plattor orsakar ett internt elektriskt fält. En dielektrikum (orange) minskar fältet och ökar kapacitansen.

Kommersiellt tillverkade kondensatorer använder vanligtvis ett fast dielektriskt material med hög permittivitet som mellanliggande medium mellan de lagrade positiva och negativa laddningarna. Detta material benämns ofta i tekniska sammanhang som kondensatorn dielektrikum .

Den mest uppenbara fördelen med att använda ett sådant dielektriskt material är att det förhindrar de ledande plattorna, på vilka laddningarna är lagrade, från att komma i direkt elektrisk kontakt. Mer signifikant är dock att en hög permittivitet tillåter en större lagrad laddning vid en given spänning. Detta kan ses genom att behandla fallet med ett linjärt dielektrikum med permittivitet ε och tjocklek d mellan två ledande plattor med enhetlig laddningstäthet σ _ε . I detta fall ges laddningstätheten av

$$\sigma _{\varepsilon }=\varepsilon {\frac {V}{d}}$$

och kapacitansen per ytenhet med

$$c={\frac {\sigma _{\varepsilon }}{V}}={\frac {\varepsilon }{d}}$$

Av detta kan man lätt se att ett större ε leder till större lagrad laddning och därmed större kapacitans.

Dielektriska material som används för kondensatorer är också valda så att de är resistenta mot jonisering . Detta tillåter kondensatorn att arbeta vid högre spänningar innan det isolerande dielektrikumet joniseras och börjar tillåta oönskad ström.

Dielektrisk resonator

Huvudartikel: Dielektrisk resonator

En dielektrisk resonatoroscillator (DRO) är en elektronisk komponent som uppvisar resonans för polarisationssvaret för ett smalt frekvensområde, vanligtvis i mikrovågsbandet. Den består av en "puck" av keramik som har en stor dielektricitetskonstant och en låg förlustfaktor . Sådana resonatorer används ofta för att tillhandahålla en frekvensreferens i en oscillatorkrets. En oskärmad dielektrisk resonator kan användas som en dielektrisk resonatorantenn (DRA).

BST tunna filmer

Från 2002 till 2004 bedrev United States Army Research Laboratory (ARL) forskning om tunnfilmsteknologi. Barium strontium titanat (BST), en ferroelektrisk tunn film, studerades för tillverkning av radiofrekvens- och mikrovågskomponenter, såsom spänningsstyrda oscillatorer, avstämbara filter och fasskiftare.

Forskningen var en del av ett försök att förse armén med mycket avstämbara, mikrovågskompatibla material för bredbandsavstämbara enheter med elektriska fält, som arbetar konsekvent i extrema temperaturer. Detta arbete förbättrade avstämningsmöjligheten för bulkbariumstrontiumtitanat, som är en tunnfilmsaktiverare för elektronikkomponenter.

I en forskningsartikel från 2004 undersökte forskare från amerikanska ARL hur små koncentrationer av acceptordopanter dramatiskt kan ändra egenskaperna hos ferroelektriska material som BST.

Forskare "dopade" BST-tunna filmer med magnesium och analyserade resultatets "struktur, mikrostruktur, ytmorfologi och film-/substratkompositionskvalitet". De Mg-dopade BST-filmerna visade "förbättrade dielektriska egenskaper, låg läckström och god avstämningsförmåga", vilket förtjänar potential för användning i mikrovågsavstämbara enheter.

Lite praktisk dielektrik

Dielektriska material kan vara fasta ämnen, vätskor eller gaser. (Ett högt vakuum kan också vara ett användbart, nästan förlustfritt dielektrikum även om dess relativa dielektricitetskonstant bara är en enhet.)

Fasta dielektrika är kanske den vanligaste dielektriken inom elektroteknik, och många fasta ämnen är mycket bra isolatorer. Några exempel inkluderar porslin , glas och de flesta plaster . Luft-, kväve- och svavelhexafluorid är de tre vanligaste gasformiga dielektrikumen .

• Industriella beläggningar såsom Parylene ger en dielektrisk barriär mellan substratet och dess miljö.
• Mineralolja används i stor utsträckning inuti elektriska transformatorer som ett flytande dielektrikum och för att hjälpa till med kylning. Dielektriska vätskor med högre dielektriska konstanter, såsom ricinolja av elektrisk kvalitet , används ofta i högspänningskondensatorer för att förhindra koronaurladdning och öka kapacitansen.
• Eftersom dielektrikum motstår flödet av elektricitet, kan ytan på ett dielektrikum behålla strängade överskott av elektriska laddningar. Detta kan inträffa av misstag när dielektrikumet gnuggas (den triboelektriska effekten) . Detta kan vara användbart, som i en Van de Graaff-generator eller elektrofor , eller så kan det vara potentiellt destruktivt som i fallet med elektrostatisk urladdning .
• Speciellt bearbetade dielektrika, kallade elektreter (som inte ska förväxlas med ferroelektriska ämnen ), kan behålla överskott av intern laddning eller "frysa i" polarisation. Elektreter har ett semipermanent elektriskt fält och är den elektrostatiska motsvarigheten till magneter. Elektreter har många praktiska tillämpningar i hemmet och industrin.
• Vissa dielektrika kan generera en potentialskillnad när de utsätts för mekanisk påfrestning , eller (motsvarande) ändra fysisk form om en extern spänning appliceras över materialet. Denna egenskap kallas piezoelektricitet . Piezoelektriska material är en annan klass av mycket användbara dielektrika.
• Vissa jonkristaller och polymerdielektrika uppvisar ett spontant dipolmoment, som kan vändas av ett externt applicerat elektriskt fält. Detta beteende kallas den ferroelektriska effekten . Dessa material är analoga med hur ferromagnetiska material beter sig inom ett externt applicerat magnetfält. Ferroelektriska material har ofta mycket höga dielektriska konstanter, vilket gör dem ganska användbara för kondensatorer.

Se även

• Klassificering av material baserad på permittivitet
• Paramagnetism
• Clausius-Mossotti relation
• Dielektrisk absorption
• Dielektriska förluster
• Dielektrisk styrka
• Dielektrisk spektroskopi
• EIA klass 1 dielektrisk
• EIA klass 2 dielektrikum
• Dielektrisk hög-k
• Låg-k dielektrikum
• läckage
• Linjär svarsfunktion
• Metamaterial
• RC fördröjning
• Roterande Brownsk rörelse
• Paschens lag – variation av gasens dielektriska styrka relaterad till tryck
• Separator (el)

Vidare läsning

•    Jackson, John David (10 augusti 1998) [1962]. Klassisk elektrodynamik (3:e upplagan). John Wiley & Sons . ISBN 978-0-471-30932-1 . OCLC 535998 .

•   Scaife, Brendan KP (3 september 1998). Principer för dielektrikum . Monographs on the Physics & Chemistry of Materials (2nd ed.). Oxford University Press . ISBN 978-0-198-56557-4 .

externa länkar

• Feynmans föreläsning om dielektrik
• Dielektrisk sfär i ett elektriskt fält
• Spridning av IT för främjande av materialvetenskap (DoITPoMS) undervisnings- och inlärningspaket "Dielektriska material" från University of Cambridge
• Texter på Wikisource:
  • " Dielektrisk ". Encyclopedia Americana . 1920.
  • " Dielektrisk ". Encyclopædia Britannica (11:e upplagan). 1911.