Finita elementmetod
| Differentialekvationer |
|---|

|
| Scope |
| Klassificering |
| Lösning |
| människor |
Finita elementmetoden ( FEM ) är en populär metod för att numeriskt lösa differentialekvationer som uppstår i ingenjörskonst och matematisk modellering . Typiska problemområden av intresse inkluderar de traditionella områdena strukturanalys , värmeöverföring , vätskeflöde , masstransport och elektromagnetisk potential .
FEM är en allmän numerisk metod för att lösa partiella differentialekvationer i två eller tre rymdvariabler (dvs. vissa gränsvärdesproblem) . För att lösa ett problem delar FEM upp ett stort system i mindre, enklare delar som kallas finita element . Detta uppnås genom en speciell rymddiskretisering i rymddimensionerna, som implementeras genom konstruktionen av ett nät av objektet: den numeriska domänen för lösningen, som har ett ändligt antal punkter. Den finita elementmetodens formulering av ett gränsvärdesproblem resulterar slutligen i ett system av algebraiska ekvationer . Metoden approximerar den okända funktionen över domänen. De enkla ekvationerna som modellerar dessa ändliga element sätts sedan ihop till ett större ekvationssystem som modellerar hela problemet. FEM approximerar sedan en lösning genom att minimera en tillhörande felfunktion via variationskalkylen .
Att studera eller analysera ett fenomen med FEM kallas ofta för finita elementanalys ( FEA ).
Grundläggande koncept
Uppdelningen av en hel domän i enklare delar har flera fördelar:
- Exakt representation av komplex geometri
- Inkluderande av olika materialegenskaper
- Enkel representation av helhetslösningen
- Fånga lokala effekter.
Typiskt arbete med metoden innefattar:
- dela upp problemets domän i en samling underdomäner, där varje underdomän representeras av en uppsättning elementekvationer till det ursprungliga problemet
- systematiskt rekombinera alla uppsättningar elementekvationer till ett globalt ekvationssystem för den slutliga beräkningen.
Det globala ekvationssystemet har kända lösningstekniker och kan beräknas från initialvärdena för det ursprungliga problemet för att få ett numeriskt svar.
I det första steget ovan är elementekvationerna enkla ekvationer som lokalt approximerar de ursprungliga komplexa ekvationerna som ska studeras, där de ursprungliga ekvationerna ofta är partiella differentialekvationer (PDE). För att förklara approximationen i denna process, introduceras den finita elementmetoden vanligtvis som ett specialfall av Galerkin-metoden . Processen, i matematiskt språk, är att konstruera en integral av den inre produkten av residual- och viktfunktionerna och sätta integralen till noll. Enkelt uttryckt är det en procedur som minimerar approximationsfelet genom att passa in testfunktioner i PDE. Residualen är felet som orsakas av försöksfunktionerna, och viktfunktionerna är polynomapproximationsfunktioner som projicerar residualen. Processen eliminerar alla rumsliga derivator från PDE, vilket approximerar PDE lokalt med
- en uppsättning algebraiska ekvationer för problem med stationära tillstånd ,
- en uppsättning vanliga differentialekvationer för transienta problem.
Dessa ekvationsuppsättningar är elementekvationerna. De är linjära om den underliggande PDE är linjär och vice versa. Algebraiska ekvationsuppsättningar som uppstår i steady-state-problemen löses med numeriska linjära algebrametoder , medan vanliga differentialekvationsuppsättningar som uppstår i de transienta problemen löses genom numerisk integration med hjälp av standardtekniker som Eulers metod eller Runge-Kutta-metoden .
I steg (2) ovan genereras ett globalt system av ekvationer från elementekvationerna genom en transformation av koordinater från underdomänernas lokala noder till domänens globala noder. Denna rumsliga transformation inkluderar lämpliga orienteringsjusteringar som tillämpas i förhållande till referenskoordinatsystemet . Processen utförs ofta av FEM-programvara med hjälp av koordinatdata som genereras från underdomänerna.
Den praktiska tillämpningen av FEM är känd som finita elementanalys (FEA). FEA som tillämpas inom teknik är ett beräkningsverktyg för att utföra ingenjörsanalys . Det inkluderar användning av mesh-genereringstekniker för att dela upp ett komplext problem i små element, samt användning av programvara kodad med en FEM-algoritm. Vid tillämpning av FEA är det komplexa problemet vanligtvis ett fysiskt system med den underliggande fysiken som Euler–Bernoullis strålekvation, värmeekvationen eller Navier - Stokes ekvationer uttryckta i antingen PDE eller integralekvationer , medan de delade små elementen i komplexa problem representerar olika områden i det fysiska systemet.
FEA kan användas för att analysera problem över komplicerade domäner (som bilar och oljeledningar), när domänen förändras (som under en solid state-reaktion med en rörlig gräns), när den önskade precisionen varierar över hela domänen, eller när lösningen saknar jämnhet. FEA-simuleringar ger en värdefull resurs eftersom de tar bort flera instanser av skapande och testning av hårda prototyper för olika högtrohetssituationer. [ citat behövs ] Till exempel, i en frontalkrocksimulering är det möjligt att öka prediktionsnoggrannheten i "viktiga" områden som bilens framsida och minska den baktill (och därmed minska kostnaden för simuleringen). Ett annat exempel skulle vara i numeriska väderförutsägelser , där det är viktigare att ha exakta förutsägelser över att utveckla mycket olinjära fenomen (som tropiska cykloner i atmosfären eller virvlar i havet) snarare än relativt lugna områden.
En tydlig, detaljerad och praktisk presentation av detta tillvägagångssätt finns i The Finite Element Method for Engineers .
Historia
Även om det är svårt att citera ett datum för uppfinningen av finita elementmetoden, har metoden sitt ursprung i behovet av att lösa komplexa elasticitets- och strukturanalysproblem inom civil- och flygteknik . Dess utveckling kan spåras tillbaka till A. Hrennikoffs och R. Courants verk i början av 1940-talet. En annan pionjär var Ioannis Argyris . I Sovjetunionen är införandet av den praktiska tillämpningen av metoden vanligtvis kopplat till namnet Leonard Oganesyan. Det återupptäcktes också självständigt i Kina av Feng Kang under det senare 1950-talet och början av 1960-talet, baserat på beräkningar av dammkonstruktioner, där det kallades den finita skillnadsmetoden baserad på variationsprincipen . Även om tillvägagångssätten som används av dessa pionjärer är olika, delar de en väsentlig egenskap: mesh- diskretisering av en kontinuerlig domän till en uppsättning diskreta underdomäner, vanligtvis kallade element.
Hrennikoffs arbete diskretiserar domänen genom att använda en gitteranalogi , medan Courants tillvägagångssätt delar upp domänen i finita triangulära subregioner för att lösa andra ordningens elliptiska partiella differentialekvationer som uppstår från problemet med torsion av en cylinder . Courants bidrag var evolutionärt och byggde på en stor mängd tidigare resultat för PDE utvecklade av Rayleigh , Ritz och Galerkin .
Den finita elementmetoden fick sin verkliga impuls på 1960- och 1970-talen genom utvecklingen av JH Argyris med medarbetare vid University of Stuttgart , RW Clough med medarbetare vid UC Berkeley , OC Zienkiewicz med medarbetare Ernest Hinton , Bruce Irons och andra vid Swansea University , Philippe G. Ciarlet vid University of Paris 6 och Richard Gallagher med medarbetare vid Cornell University . Ytterligare impulser gavs under dessa år av tillgängliga finita elementprogram med öppen källkod. NASA sponsrade den ursprungliga versionen av NASTRAN , och UC Berkeley gjorde det finita elementprogrammet SAP IV allmänt tillgängligt. I Norge utvecklade fartygsklassificeringssällskapet Det Norske Veritas (numera DNV GL ) Sesam 1969 för användning vid analys av fartyg. En rigorös matematisk grund för den finita elementmetoden gavs 1973 med publikationen av Strang och Fix . Metoden har sedan dess generaliserats för numerisk modellering av fysiska system inom en mängd olika tekniska discipliner, t.ex. elektromagnetism , värmeöverföring och vätskedynamik .
Teknisk diskussion
Strukturen för finita elementmetoder
En finita elementmetod kännetecknas av en variationsformulering , en diskretiseringsstrategi, en eller flera lösningsalgoritmer och efterbehandlingsprocedurer.
Exempel på variationsformuleringen är Galerkinmetoden , den diskontinuerliga Galerkinmetoden, blandade metoder etc.
En diskretiseringsstrategi förstås som en tydligt definierad uppsättning procedurer som täcker (a) skapandet av finita elementmaskor, (b) definitionen av basfunktion på referenselement (även kallade formfunktioner) och (c) kartläggning av referens element på elementen i nätet. Exempel på diskretiseringsstrategier är h-versionen, p-versionen , hp-versionen , x-FEM , isogeometrisk analys etc. Varje diskretiseringsstrategi har vissa fördelar och nackdelar. Ett rimligt kriterium för att välja en diskretiseringsstrategi är att realisera nästan optimal prestanda för den bredaste uppsättningen matematiska modeller i en viss modellklass.
Olika numeriska lösningsalgoritmer kan klassificeras i två breda kategorier; direkta och iterativa lösare. Dessa algoritmer är utformade för att utnyttja glesheten av matriser som beror på valen av variationsformulering och diskretiseringsstrategi.
Efterbehandlingsprocedurer är utformade för att extrahera data av intresse från en finita elementlösning. För att uppfylla kraven på lösningsverifiering måste efterbehandlare tillhandahålla en uppskattning av fel i efterhand när det gäller de kvantiteter som är av intresse. När approximationsfelen är större än vad som anses acceptabelt måste diskretiseringen ändras antingen genom en automatiserad adaptiv process eller genom analytikerns agerande. Det finns några mycket effektiva postprocessorer som tillhandahåller förverkligandet av superkonvergens .
Illustrativa problem P1 och P2
Följande två problem visar den finita elementmetoden.
P1 är ett endimensionellt problem
där ges, är en okänd funktion av , och är andraderivatan av med respekt för .
P2 är ett tvådimensionellt problem ( Dirichlet problem )
där är ett anslutet öppet område i planet vars gräns är fin (t.ex. ett jämnt grenrör eller en polygon ), och och betecknar andraderivatorna med avseende på och , respektive.
Problemet P1 kan lösas direkt genom att beräkna antiderivator . Den här metoden för att lösa gränsvärdesproblemet (BVP) fungerar dock bara när det finns en rumslig dimension och generaliserar inte till högre dimensionella problem eller problem som . Av denna anledning kommer vi att utveckla den finita elementmetoden för P1 och skissera dess generalisering till P2.
Vår förklaring kommer att fortsätta i två steg, som speglar två viktiga steg man måste ta för att lösa ett gränsvärdesproblem (BVP) med hjälp av FEM.
- I det första steget omformulerar man den ursprungliga BVP i dess svaga form. Lite eller ingen beräkning krävs vanligtvis för detta steg. Förvandlingen görs för hand på papper.
- Det andra steget är diskretiseringen, där den svaga formen diskretiseras i ett ändligt dimensionellt utrymme.
Efter detta andra steg har vi konkreta formler för ett stort men änddimensionellt linjärt problem vars lösning ungefär kommer att lösa den ursprungliga BVP. Detta finita dimensionella problem implementeras sedan på en dator .
Svag formulering
Det första steget är att omvandla P1 och P2 till motsvarande svaga formuleringar .
Den svaga formen av P1
Om löser P1, då för varje jämn funktion som uppfyller förskjutningsgränsvillkoren, dvs vid och , vi har
|
|
|
() |
Omvänt, om med uppfyller (1) för varje jämn funktion då kan man visa att denna kommer att lösa P1. Beviset är lättare för två gånger kontinuerligt differentierbar medelvärdessats ) , men kan också bevisas i en fördelningsmässig mening.
Vi definierar en ny operator eller kartlägger genom att använda integrering av delar till höger om (1):
-
()
där vi har använt antagandet att .
Den svaga formen av P2
Om vi integrerar med delar som använder en form av Greens identiteter ser vi att om löser P2, så kan vi definiera för vilken av
där anger gradienten och anger prickprodukten i det tvådimensionella planet. Än en gång omvandlas till en inre produkt på ett lämpligt utrymme av en gång differentierbara funktioner av som är noll på . Vi har också antagit att (se Sobolev-mellanslag ). Lösningens existens och unika kan också visas.
Ett bevis på lösningens existens och unikhet
Vi kan löst tänka på att är de absolut kontinuerliga funktionerna av som är vid och (se Sobolev-mellanslag ). Sådana funktioner är (svagt) en gång differentierbara och det visar sig att den symmetriska bilinjära kartan sedan definierar en inre produkt som gör i ett Hilbert-utrymme (ett detaljerat bevis är inte trivialt). Å andra sidan är den vänstra sidan också en inre produkt, denna gång på Lp-utrymmet . En tillämpning av Riesz-representationssatsen för Hilbert-rum visar att det finns en unik -lösning (2) och därför P1. Denna lösning är a-priori endast en medlem av men med elliptisk regelbundenhet blir den jämn om är .
Diskretisering
P1 och P2 är redo att diskretiseras vilket leder till ett vanligt delproblem (3). Grundidén är att ersätta det oändliga-dimensionella linjära problemet:
- Hitta så att
med en finitdimensionell version:
-
Hitta så att()
där är ett ändligt dimensionellt delrum av . Det finns många möjliga val för (en möjlighet leder till spektralmetoden ). För finita elementmetoden tar vi emellertid för att vara ett utrymme av styckevisa polynomfunktioner.
För problem P1
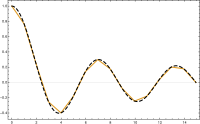
Vi tar intervallet , välj värden av med och vi definierar med:
där vi definierar och . Observera att funktioner i inte är differentierbara enligt den elementära definitionen av kalkyl. Faktum är att om så är derivatan vanligtvis inte definierad vid någon k . Däremot finns derivatan vid vartannat värde på och man kan använda denna derivata för att integrera med delar .
För problem P2
Vi behöver för att vara en uppsättning funktioner av . I figuren till höger har vi illustrerat en triangulering av en 15-sidig polygonal region i planet (nedan), och en bitvis linjär funktion (ovanför, i färg) av denna polygon som är linjär på varje triangel i trianguleringen; utrymmet skulle bestå av funktioner som är linjära på varje triangel i den valda trianguleringen.
Man hoppas att när det underliggande triangulära nätet blir finare och finare, kommer lösningen av det diskreta problemet (3) i någon mening att konvergera till lösningen av det ursprungliga gränsvärdesproblemet P2. För att mäta denna maskfinhet, indexeras trianguleringen med en realvärderad parameter som man tar för att vara mycket liten. Denna parameter kommer att vara relaterad till storleken på den största eller genomsnittliga triangeln i trianguleringen. När vi förfinar trianguleringen måste utrymmet för bitvis linjära funktioner . Av denna anledning läser man ofta istället för i litteraturen. Eftersom vi inte utför en sådan analys kommer vi inte att använda denna notation.
Att välja en grund
För att slutföra diskretiseringen måste vi välja en grund av . I det endimensionella fallet kommer vi för varje kontrollpunkt i vars värde är vid och noll vid varje dvs.
för ; denna bas är en förskjuten och skalad tältfunktion . För det tvådimensionella fallet väljer vi igen en basfunktion per vertex av trianguleringen av det plana området . Funktionen är den unika funktionen för vars värde är vid och noll vid varje .
Beroende på författaren hänvisar ordet "element" i "finita elementmetoden" antingen till trianglarna i domänen, den bitvis linjära basfunktionen eller båda. Så till exempel kan en författare som är intresserad av krökta domäner ersätta trianglarna med krökta primitiver, och så kan beskriva elementen som krökt. Å andra sidan ersätter vissa författare "styckvis linjär" med "styckvis kvadratisk" eller till och med "styckvis polynom". Författaren kan då säga "högre ordningselement" istället för "polynom med högre grad". Den finita elementmetoden är inte begränsad till trianglar (eller tetraedrar i 3-d, eller högre ordningens simplex i flerdimensionella utrymmen), utan kan definieras på fyrsidiga underdomäner (hexaedrar, prismor eller pyramider i 3-d, och så vidare) . Former av högre ordning (krökt element) kan definieras med polynomiska och även icke-polynomformer (t.ex. ellips eller cirkel).
Exempel på metoder som använder högre grad av styckvis polynombasfunktioner är hp-FEM och spektral FEM .
Mer avancerade implementeringar (adaptiva finita elementmetoder) använder en metod för att bedöma kvaliteten på resultaten (baserat på feluppskattningsteori) och modifiera nätet under lösningen i syfte att uppnå en ungefärlig lösning inom vissa gränser från den exakta lösningen av kontinuumproblemet . Mesh adaptivitet kan använda olika tekniker, de mest populära är:
- rörliga noder (r-anpassning)
- raffinerande (och oraffinerade) element (h-adaptivitet)
- ändra ordning av basfunktioner (p-adaptivitet)
- kombinationer av ovanstående ( hp-adaptivity ).
Litet stöd för grunden

Den främsta fördelen med detta val av bas är att de inre produkterna
och
kommer att vara noll för nästan alla . (Matrisen som innehåller i platsen är känd som Gramian matris .) I det endimensionella fallet är stödet för intervallet . Därför är integranderna för och är identiskt noll när .
På liknande sätt, i det plana fallet, om och inte delar en kant av trianguleringen, då integralerna
och
är båda noll.
Problemets matrisform
Om vi skriver och sedan problem (3), tar för , blir
-
för
()
Om vi betecknar med och kolumnvektorerna och och om vi låter
och
vara matriser vars poster är
och
då kan vi omformulera (4) som
|
|
|
() |
Det är inte nödvändigt att anta . För en allmän funktion , problem (3) med för blir faktiskt enklare, eftersom ingen matris används,
|
|
|
() |
där och för .
Som vi har diskuterat tidigare är de flesta ingångarna för och noll eftersom basfunktionerna har litet stöd. Så vi måste nu lösa ett linjärt system i det okända där de flesta ingångarna i matrisen som vi behöver invertera, är noll.
Sådana matriser är kända som glesa matriser , och det finns effektiva lösare för sådana problem (mycket effektivare än att faktiskt invertera matrisen.) Dessutom är symmetrisk och positiv bestämd, så en teknik som den konjugerade gradienten metoden gynnas. För problem som inte är för stora fungerar fortfarande glesa LU-sönderdelningar och Cholesky-sönderdelningar bra. Till exempel MATLAB: s backslash-operator (som använder sparse LU, sparse Cholesky och andra faktoriseringsmetoder) vara tillräcklig för maskor med hundra tusen hörn.
Matrisen kallas vanligtvis för styvhetsmatrisen , medan matrisen kallas massmatrisen .
Allmän form av finita elementmetoden
I allmänhet kännetecknas den finita elementmetoden av följande process.
- Man väljer ett rutnät för . I den föregående behandlingen bestod rutnätet av trianglar, men man kan också använda kvadrater eller krökta polygoner.
- Sedan väljer man basfunktioner. I vår diskussion använde vi styckvis linjära basfunktioner, men det är också vanligt att använda styckvisa polynombasfunktioner.
Separat hänsyn är jämnheten hos basfunktionerna. För andra ordningens elliptiska gränsvärdeproblem räcker det med en styckevis polynombasfunktion som bara är kontinuerlig (dvs. derivatorna är diskontinuerliga.) För partiella differentialekvationer av högre ordningen måste man använda jämnare basfunktioner. Till exempel, för ett fjärde ordningens problem som , kan man använda bitvis kvadratiska basfunktioner som är .
Ett annat övervägande är förhållandet mellan det ändligt dimensionella utrymmet och dess oändliga dimensionella motsvarighet, i exemplen ovan . En överensstämmande elementmetod är en där utrymme är ett underutrymme till elementutrymmet för det kontinuerliga problemet. Exemplet ovan är en sådan metod. Om detta villkor inte är uppfyllt, erhåller vi en icke-överensstämmande elementmetod, ett exempel på vilket är utrymmet av bitvis linjära funktioner över nätet som är kontinuerliga vid varje kantmittpunkt. Eftersom dessa funktioner i allmänhet är diskontinuerliga längs kanterna, är detta änddimensionella utrymme inte ett delrum av det ursprungliga .
Vanligtvis har man en algoritm för att ta ett givet nät och dela upp det. Om huvudmetoden för att öka precisionen är att dela upp nätet, har man en h -metod ( h är vanligtvis diametern på det största elementet i nätet.) På detta sätt, om man visar att felet med ett rutnät avgränsas ovan av , för vissa p , då har man en ordning p metod. Under vissa hypoteser (till exempel om domänen är konvex) kommer en bitvis polynom av ordningen -metod att ha ett fel av ordningen .
Om man istället för att göra h mindre, ökar graden av polynomen som används i basfunktionen, har man en p -metod. Om man kombinerar dessa två förfiningstyper får man en hp -metod ( hp-FEM ) . I hp-FEM kan polynomgraderna variera från element till element. Högordningsmetoder med stort enhetligt p kallas spektrala finita elementmetoder ( SFEM ). Dessa ska inte förväxlas med spektrala metoder .
För vektorpartiella differentialekvationer kan basfunktionerna anta värden i .
Olika typer av finita elementmetoder
AEM
Applied Element Method eller AEM kombinerar funktioner i både FEM och Discrete element method , eller (DEM).
A-FEM
Augmented-Finite Element Method introduceras av Yang och Lui vars mål var att modellera de svaga och starka diskontinuiteterna utan behov av extra DoFs som i PuM anges.
Generaliserad finita elementmetod
Den generaliserade finita elementmetoden (GFEM) använder lokala rum som består av funktioner, inte nödvändigtvis polynom, som återspeglar tillgänglig information om den okända lösningen och därmed säkerställer god lokal approximation. Sedan används en enhetspartition för att "binda" dessa utrymmen tillsammans för att bilda det approximativa underrummet. Effektiviteten av GFEM har visats när den tillämpas på problem med domäner som har komplicerade gränser, problem med mikroskalor och problem med gränsskikt.
Mixed finita element-metod
Den blandade finita elementmetoden är en typ av finita elementmetod där extra oberoende variabler introduceras som nodvariabler under diskretiseringen av ett partiellt differentialekvationsproblem.
Variabel – polynom
hp -FEM kombinerar adaptivt element med variabel storlek h och polynomgrad p för att uppnå exceptionellt snabba, exponentiella konvergenshastigheter.
hpk-FEM
hpk-FEM kombinerar adaptivt element med variabel storlek h , polynomgraden för de lokala approximationerna p och global differentiabilitet för de lokala approximationerna ( k-1) för att uppnå bästa konvergenshastigheter.
XFEM
Den utökade finita elementmetoden (XFEM) är en numerisk teknik baserad på den generaliserade finita elementmetoden (GFEM) och partition of unity-metoden (PUM). Den utökar den klassiska finita elementmetoden genom att berika lösningsutrymmet för lösningar till differentialekvationer med diskontinuerliga funktioner. Utökade finita elementmetoder berikar approximationsutrymmet så att det naturligt kan reproducera det utmanande särdrag som är förknippat med problemet av intresse: diskontinuiteten, singulariteten, gränsskiktet etc. Det visades att för vissa problem, en sådan inbäddning av problemets särdrag i approximationsutrymmet kan avsevärt förbättra konvergenshastigheten och noggrannheten. Dessutom undertrycker behandling av problem med diskontinuiteter med XFEM behovet av att maska in och åter maska diskontinuitetsytorna, vilket minskar de beräkningskostnader och projektionsfel som är förknippade med konventionella finita elementmetoder, till priset av att begränsa diskontinuiteterna till maskkanter.
Flera forskningskoder implementerar denna teknik i olika grader: 1. GetFEM++ 2. xfem++ 3. openxfem++
XFEM har också implementerats i koder som Altair Radios, ASTER, Morfeo och Abaqus. Det antas i allt högre grad av andra kommersiella finita element-programvara, med några plugins och faktiska kärnimplementationer tillgängliga (ANSYS, SAMCEF, OOFELIE, etc.).
Scaled boundary finite element method (SBFEM)
Införandet av den skalade gränsen finita elementmetoden (SBFEM) kom från Song och Wolf (1997). SBFEM har varit ett av de mest lönsamma bidragen inom området för numerisk analys av sprickmekaniska problem. Det är en semi-analytisk fundamental-lösningslös metod som kombinerar fördelarna med både finita element formuleringar och procedurer och gränselement diskretisering. Men till skillnad från gränselementmetoden krävs ingen fundamental differentiallösning.
S-FEM
S-FEM, Smoothed Finite Element Methods, är en speciell klass av numeriska simuleringsalgoritmer för simulering av fysiska fenomen. Den utvecklades genom att kombinera meshfria metoder med finita elementmetoden.
Spektralelementmetod
Spektralelementmetoder kombinerar den geometriska flexibiliteten hos finita element och den akuta noggrannheten hos spektrala metoder. Spektralmetoder är den ungefärliga lösningen av partiella ekvationer med svag form som är baserade på lagrangiska interpolanter av hög ordning och endast används med vissa kvadraturregler.
Meshfria metoder
Diskontinuerliga Galerkin-metoder
Finita element gränsanalys
Sträckt rutnätsmetod
Loubignac iteration
Loubignac-iteration är en iterativ metod i finita elementmetoder.
Crystal plasticity finite element method (CPFEM)
Crystal plasticity finite element method (CPFEM) är ett avancerat numeriskt verktyg utvecklat av Franz Roters. Metaller kan betraktas som kristallaggregat och de uppträder anisotropi under deformation, till exempel, onormal stress och töjningslokalisering. CPFEM baserat på glidning (skjuvtöjningshastighet) kan beräkna dislokation, kristallorientering och annan texturinformation för att beakta kristallanisotropi under rutinen. Nu har det tillämpats i den numeriska studien av materialdeformation, ytjämnhet, brott och så vidare.
Virtuell elementmetod (VEM)
Den virtuella elementmetoden (VEM), introducerad av Beirão da Veiga et al. (2013) som en förlängning av mimetiska finita differensmetoder (MFD), är en generalisering av standardmetoden för finita element för godtyckliga elementgeometrier. Detta tillåter tillträde av allmänna polygoner (eller polyedrar i 3D) som är mycket oregelbundna och icke-konvexa till formen. Namnet virtuell härrör från det faktum att kunskap om den lokala formfunktionsbasen inte krävs, och faktiskt aldrig explicit beräknas.
Länk med gradientdiskretiseringsmetoden
Vissa typer av finita elementmetoder (överensstämmande, icke-överensstämmande, blandade finita elementmetoder) är speciella fall av gradientdiskretiseringsmetoden ( GDM) . Därför gäller konvergensegenskaperna för GDM, som är etablerade för en serie problem (linjära och icke-linjära elliptiska problem, linjära, olinjära och degenererade paraboliska problem), lika bra för dessa speciella FEM.
Jämförelse med finita differensmetoden
Den finita differensmetoden (FDM) är ett alternativt sätt att approximera lösningar av PDE:er. Skillnaderna mellan FEM och FDM är:
- Den mest attraktiva egenskapen hos FEM är dess förmåga att hantera komplicerade geometrier (och gränser) med relativ lätthet. Medan FDM i sin grundform är begränsad till att hantera rektangulära former och enkla förändringar därav, är hanteringen av geometrier i FEM teoretiskt okomplicerad.
- FDM används vanligtvis inte för oregelbundna CAD-geometrier utan oftare rektangulära eller blockformade modeller.
- FEM tillåter generellt mer flexibel mesh-anpassning än FDM.
- Det mest attraktiva med ändliga skillnader är att det är mycket lätt att implementera.
- Det finns flera sätt att betrakta FDM som ett specialfall av FEM-metoden. Till exempel är första ordningens FEM identisk med FDM för Poissons ekvation , om problemet diskretiseras av ett regelbundet rektangulärt nät med varje rektangel delad i två trianglar.
- Det finns skäl att betrakta den matematiska grunden för den finita elementapproximationen mer ljud, till exempel eftersom kvaliteten på approximationen mellan rutnätspunkter är dålig i FDM.
- Kvaliteten på en FEM-approximation är ofta högre än i motsvarande FDM-upplägg, men detta är extremt problemberoende och flera exempel på motsatsen kan ges.
Generellt är FEM den valda metoden i alla typer av analys inom strukturell mekanik (dvs. att lösa för deformation och spänningar i fasta kroppar eller dynamik hos strukturer) medan beräkningsvätskedynamik (CFD) tenderar att använda FDM eller andra metoder som finita volymmetoden ( FVM). CFD-problem kräver vanligtvis diskretisering av problemet till ett stort antal celler/gridpoints (miljoner och fler), därför gynnar kostnaden för lösningen enklare, lägre ordningsapproximation inom varje cell. Detta gäller särskilt för problem med "externt flöde", som luftflödet runt bilen eller flygplanet, eller vädersimulering.
Ansökan
En mängd olika specialiseringar under paraplyet av maskinteknikdisciplinen (som flyg-, biomekanisk och fordonsindustri) använder vanligtvis integrerad FEM i design och utveckling av sina produkter. Flera moderna FEM-paket inkluderar specifika komponenter som termiska, elektromagnetiska, flytande och strukturella arbetsmiljöer. I en strukturell simulering hjälper FEM enormt med att producera styvhet och styrka visualiseringar och även att minimera vikt, material och kostnader.
FEM tillåter detaljerad visualisering av var strukturer böjer eller vrider sig, och indikerar fördelningen av spänningar och förskjutningar. FEM-programvaran tillhandahåller ett brett utbud av simuleringsalternativ för att kontrollera komplexiteten i både modellering och analys av ett system. På liknande sätt kan den önskade noggrannhetsnivån som krävs och tillhörande krav på beräkningstid hanteras samtidigt för att hantera de flesta tekniska tillämpningar. FEM tillåter att hela konstruktioner konstrueras, förfinas och optimeras innan konstruktionen tillverkas. Nätet är en integrerad del av modellen och det måste kontrolleras noggrant för att ge bästa resultat. I allmänhet är ju högre antalet element i ett nät, desto mer exakt lösning av det diskretiserade problemet. Det finns dock ett värde vid vilket resultaten konvergerar och ytterligare nätförfining ökar inte noggrannheten.
Detta kraftfulla designverktyg har avsevärt förbättrat både standarden för teknisk design och metodiken för designprocessen i många industriella tillämpningar. Införandet av FEM har avsevärt minskat tiden för att ta produkter från idé till produktionslinje. Det är främst genom förbättrade initiala prototypdesigner med FEM som testning och utveckling har accelererats. Sammanfattningsvis inkluderar fördelarna med FEM ökad noggrannhet, förbättrad design och bättre insikt i kritiska designparametrar, virtuella prototyper, färre hårdvaruprototyper, en snabbare och billigare designcykel, ökad produktivitet och ökade intäkter.
På 1990-talet föreslogs FEM för användning i stokastisk modellering för att numeriskt lösa sannolikhetsmodeller och senare för tillförlitlighetsbedömning.
Se även
- Tillämpad elementmetod
- Gränselementmetod
- Céas lemma
- Datorexperiment
- Direkt styvhetsmetod
- Optimering av diskontinuitetslayout
- Diskret elementmetod
- Ändlig skillnadsmetod
- Finita element maskin
- Finita elementmetod inom konstruktionsmekanik
- Metod med ändlig volym
- Ändlig volymmetod för ostadigt flöde
- Metod med oändliga element
- Intervall ändligt element
- Isogeometrisk analys
- Lattice Boltzmann metoder
- Lista över ändliga element mjukvarupaket
- Meshfria metoder
- Rörlig cellulär automat
- Multidisciplinär designoptimering
- Multifysik
- Patch test
- Rayleigh-Ritz-metoden
- Rymdkartläggning
- STRAND7
- Tessellation (datorgrafik)
- Försvagad svag form
Vidare läsning
- G. Allaire och A. Craig: Numerisk analys och optimering: En introduktion till matematisk modellering och numerisk simulering .
- KJ Bathe: Numeriska metoder i finita elementanalys , Prentice-Hall (1976).
- Thomas JR Hughes: Den finita elementmetoden: linjär statisk och dynamisk finita elementanalys, Prentice-Hall (1987).
- J. Chaskalovic: Finite Elements Methods for Engineering Sciences , Springer Verlag, (2008).
- Endre Süli : Finita elementmetoder för partiella differentialekvationer .
- OC Zienkiewicz, RL Taylor, JZ Zhu: The Finite Element Method: Dess Basis and Fundamentals , Butterworth-Heinemann (2005).
- N. Ottosen, H. Petersson : Introduktion till finita elementmetoden, Prentice-Hall (1992).
- Zohdi, TI (2018) En finita element primer för nybörjare-förlängd version inklusive provtester och projekt. Andra upplagan https://link.springer.com/book/10.1007/978-3-319-70428-9
















































![{\displaystyle V=\{v:[0,1]\rightarrow \mathbb {R} \;:v{\mbox{ is continuous, }}v|_{[x_{k},x_{k+1}]}{\mbox{ is linear for }}k=0,\dots ,n{\mbox{, and }}v(0)=v(1)=0\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d72f354ee5b50866296ad9e758f442f6a32d4b32)









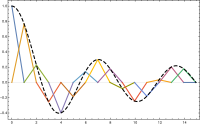




![{\displaystyle v_{k}(x)={\begin{cases}{x-x_{k-1} \over x_{k}\,-x_{k-1}}&{\mbox{ if }}x\in [x_{k-1},x_{k}],\\{x_{k+1}\,-x \over x_{k+1}\,-x_{k}}&{\mbox{ if }}x\in [x_{k},x_{k+1}],\\0&{\mbox{ otherwise}},\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1d8df33dbf412ea446944402c80c7cab51ecd7e)










![[x_{k-1},x_{k+1}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9ab905e7068db95aeddfd9f0fa55af0e0363843)




































