Gyroelång bikupa

Uppsättning av gyrolånga bikupoler

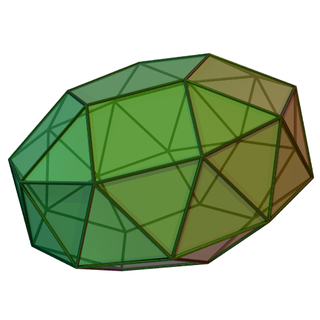Exempel på femkantig form
Ansikten	6n trianglar 2n rutor 2 n-gon
Kanter	16 n
Vertices	6 n
Symmetrigrupp	D n , [n,2] + , (n22)
Rotationsgrupp	D n , [n,2] + , (n22)
Egenskaper	konvex, kiral

I geometri är de gyrolånga bikuporna en oändlig uppsättning polyedrar , konstruerade genom att angränsa två n-gonala kupoler till en n-gonal antiprisma . Den triangulära, fyrkantiga och femkantiga gyrolånga bikupan är tre av fem Johnson solids som är kirala , vilket betyder att de har en "vänsterhänt" och en "högerhänt" form.

Att ansluta två triangulära prismor till en kub genererar också en polyeder, men har intilliggande parallella ytor, så är inte en Johnson solid. Den hexagonala formen är också en polygon, men har koplanära ytor. Högre former kan konstrueras utan regelbundna ytor.

Bild cw	Bild ccw	namn	Ansikten
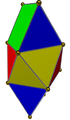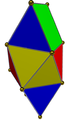
		Gyroelång digonal bikupa	4 trianglar, 4 rutor
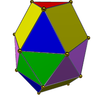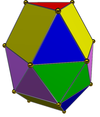
		Gyroelång triangulär bikupa ( J44 )	6+2 trianglar, 6 rutor
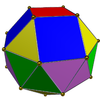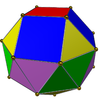		Gyroelång fyrkantig bikupa ( J45 )	8 trianglar, 8+2 rutor
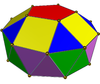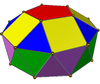		Gyrolånga femkantiga bikupa ( J46 )	30 trianglar, 10 rutor, 2 femhörningar
		Gyroelång sexkantig bikupa	12 trianglar, 24 rutor, 2 hexagoner

Se även

• Avlång kupol

• Norman W. Johnson , "Convex Solids with Regular Faces", Canadian Journal of Mathematics, 18 , 1966, sidorna 169–200. Innehåller den ursprungliga uppräkningen av de 92 fasta ämnena och gissningen att det inte finns några andra.
• Victor A. Zalgaller (1969). Konvex polyeder med regelbundna ytor . Konsultbyrån. Inget ISBN. Det första beviset på att det bara finns 92 Johnson-fastämnen.