Fyrkantig gyrobicupola
| Fyrkantig gyrobicupola | |
|---|---|
 | |
| Typ |
Bicupola , Johnson J 28 – J 29 – J 30 |
| Ansikten |
8 trianglar 2+8 rutor |
| Kanter | 32 |
| Vertices | 16 |
| Vertex-konfiguration | 8(3.4.3.4) 8(3.4 3 ) |
| Symmetrigrupp | D 4d |
| Dubbel polyeder | Långsträckt kvadratisk trapets |
| Egenskaper | konvex |
| Netto | |
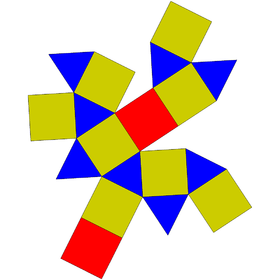 | |
Inom geometri är den kvadratiska gyrobicupola en av Johnsons fasta ämnen ( J 29 ). Liksom den fyrkantiga ortobikupan ( J 28 ) kan den erhållas genom att sammanfoga två fyrkantiga kupoler ( J 4 ) längs deras baser. Skillnaden är att i denna solida rotation roteras de två halvorna 45 grader i förhållande till varandra.
En Johnson solid är en av 92 strikt konvexa polyedrar som är sammansatta av regelbundna polygonytor men som inte är enhetliga polyedrar (det vill säga de är inte platoniska solids , Archimedean solids , prismor , eller antiprismor ). De namngavs av Norman Johnson , som först listade dessa polyedrar 1966.
Den fyrkantiga gyrobicupola är den andra i en oändlig uppsättning av gyrobicupolae .
Besläktad med den fyrkantiga gyrobikupan är den långsträckta fyrkantiga gyrobikupan . Denna polyeder skapas när ett åttakantigt prisma sätts in mellan de två halvorna av den fyrkantiga gyrobikupan. Det diskuteras huruvida den långsträckta fyrkantiga gyrobicupolan är en arkimedisk fast substans , eftersom den inte är särskilt symmetrisk, även om den uppfyller alla andra standarder som krävs för att vara en arkimedisk fast substans.
Formler
Följande formler för volym och ytarea kan användas om alla ytor är regelbundna , med kantlängd a :
Besläktade polyedrar och honungskakor
Den fyrkantiga gyrobicupolan bildar rymdfyllande bikakor med tetraedrar , kuber och cuboctaedra ; och med tetraedrar, fyrkantiga pyramider och långsträckta fyrkantiga bipyramider . (Den senare enheten kan delas upp i långsträckta fyrkantiga pyramider , kuber och/eller fyrkantiga pyramider).

