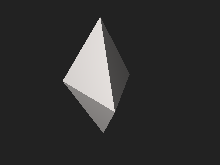Triangulär bipyramid

För den relaterade molekylär geometriska strukturen, se Trigonal bipyramid molekylär geometri .

Triangulär bipyramid
Typ	Bipyramid , Johnson J 11 – J 12 – J 13
Ansikten	6 trianglar
Kanter	9
Vertices	5
Schläfli symbol	{ } + {3}
Coxeter diagram
Symmetrigrupp	D 3h , [3,2], (*223), order 12
Rotationsgrupp	D3 , [3,2] + , (223), ordning 6
Dubbel polyeder	Trekantsprisma
Ansiktskonfiguration	V3.4.4
Egenskaper	Konvex , ansiktstransitiv

3D-modell av en triangulär bipyramid

Netto

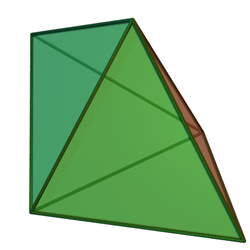
I geometri är den triangulära bipyramiden (eller dipyramiden ) en typ av hexahedron , som är den första i den oändliga uppsättningen av ansiktsövergående bipyramider. Det är dual av det triangulära prismat med 6 likbenta triangelytor.

Som namnet antyder kan den konstrueras genom att sammanfoga två tetraedrar längs en sida. Även om alla dess ytor är kongruenta och det solida är ansiktstransitivt , är det inte ett platoniskt solid eftersom vissa hörn gränsar till tre sidor och andra gränsar till fyra.

Bipyramiden vars sex ytor alla är liksidiga trianglar är en av Johnson solids , ( J ₁₂ ). En Johnson solid är en av 92 strikt konvexa polyedrar som är sammansatta av regelbundna polygonytor men som inte är enhetliga polyedrar (det vill säga de är inte platoniska solids , Archimedean solids , prismor , eller antiprismor ). De namngavs av Norman Johnson , som först listade dessa polyedrar 1966. Som en Johnson solid med alla ansikten liksidiga trianglar, är det också en deltahedron .

Formler

Följande formler för höjd ( $H$ ), yta ( $A$ ) och volym ( $V$ ) kan användas om alla ytor är regelbundna, med kantlängd ${\ displaystyle L}$ :

${\displaystyle H=L\cdot {\frac {2{\sqrt {6}}}{3}}\approx L\cdot 1.632993162$

$A=L^{2}\cdot {\frac {3{\sqrt {3}}}{2}}\approx L^{2}\cdot 2.598076211$

$V=L^{3}\cdot {\frac {\sqrt {2}}{6}}\approx L^{3}\cdot 0,235702260$

Dubbel polyeder

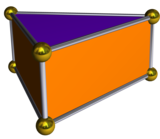
Den dubbla polyhedronen i den triangulära bipyramiden är det triangulära prismat , med fem sidor: två parallella liksidiga trianglar sammanlänkade med en kedja av tre rektanglar. Även om det triangulära prismat har en form som är en likformig polyeder (med fyrkantiga ytor), har den dubbla av Johnson solid form av bipyramiden rektangulära snarare än kvadratiska ytor, och är inte enhetlig.

Dubbel triangulär bipyramid	Netto av dubbel

Besläktade polyedrar och honungskakor

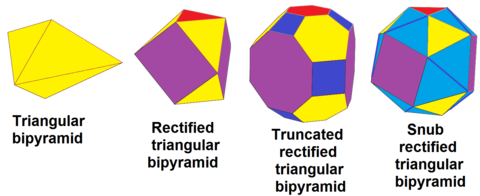
Den triangulära bipyramiden , dt{2,3}, kan i sekvens korrigeras , rdt{2,3}, trunkerad , trdt{2,3} och alternerad ( avstängd ), srdt{2,3}:

Den triangulära bipyramiden kan konstrueras genom förstärkning av mindre, närmare bestämt två staplade vanliga oktaedrar med 3 triangulära bipyramider lagt till runt sidorna, och 1 tetraeder ovanför och under. Denna polyeder har 24 liksidiga triangelytor , men den är inte en Johnson solid eftersom den har koplanära ytor. Det är en coplanar 24-triangel deltahedron . Denna polyeder existerar som förstärkning av celler i en roterande alternerad kubisk bikaka . Större triangulära polyedrar kan genereras på liknande sätt, som 9, 16 eller 25 trianglar per större triangelyta, sett som en sektion av en triangulär plattsättning .

Den triangulära bipyramiden kan bilda en tessellation av rymden med oktaedrar eller med trunkerade tetraedrar .

Lager av den enhetliga kvartskubiska bikakan kan flyttas för att para ihop vanliga tetraedriska celler som kombineras till triangulära bipyramider.

Den roterande tetraedriska-oktaedriska bikakan har par av intilliggande regelbundna tetraedrar som kan ses som triangulära bipyramider.

När den projiceras på en sfär, liknar den en sammansättning av en trigonal hosohedron och en trigonal dihedron . Det är en del av en oändlig serie av dubbla par sammansättningar av vanliga polyedrar som projiceras på sfärer. Den triangulära bipyramiden kan hänvisas till som en deltoidal hexaeder för överensstämmelse med de andra fasta ämnena i serien, även om "deltoiderna" är trianglar istället för drakar i detta fall, eftersom vinkeln från dihedronen är 180 grader.

* n 32 symmetrimutation av dubbla expanderade plattsättningar: V3.4. n .4

Symmetri * n 32 [n,3]	Sfärisk				Euklid.	Kompakt hyperb.		Paraco.
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
Figur Config.	V3.4.2.4	V3.4.3.4	V3.4.4.4	V3.4.5.4	V3.4.6.4	V3.4.7.4	V3.4.8.4	V3.4.∞.4

Se även

• Trigonal bipyramidal molekylär geometri
• Boerdijk–Coxeter helix , en förlängning av den triangulära bipyramiden genom att lägga till fler tetraedrar

"Vanliga" höger (symmetriska) n- gonala bipyramider:

Bipyramid namn	Digonal bipyramid	Triangulär bipyramid (Se: J 12 )	Fyrkantig bipyramid (Se: O )	Pentagonal bipyramid (Se: J 13 )	Hexagonal bipyramid	Heptagonal bipyramid	Åttakantig bipyramid	Enneagonal bipyramid	Dekagonal bipyramid	...	Apeirogonal bipyramid
Polyeder bild										...
Sfärisk kakelbild										Plan kakel bild
Ansiktskonfiguration.	V2.4.4	V3.4.4	V4.4.4	V5.4.4	V6.4.4	V7.4.4	V8.4.4	V9.4.4	V10.4.4	...	V∞.4.4
Coxeter diagram										...

externa länkar

• Eric W. Weisstein , Triangulär dipyramid ( Johnson solid ) på MathWorld .
• Conway Notation för Polyhedra Prova: dP3