Snub disfenoid

Snub disfenoid
Typ	Johnson J 83 – J 84 – J 85
Ansikten	4+8 trianglar
Kanter	18
Vertices	8
Vertex-konfiguration	4(3 4 ) 4(3 5 )
Symmetrigrupp	D 2d
Dubbel polyeder	Avlångt gyrobifastigium
Egenskaper	konvex , deltaeder
Netto

3D-modell av en snub-disfenoid

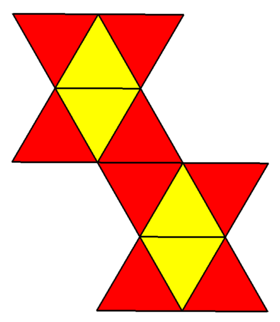Inom geometrin är den snubbade disfenoiden , siamesisk dodekaeder , triangulär dodekaeder , trigonal dodekaeder eller dodekadeltaeder en konvex polyeder med tolv liksidiga trianglar som sina ytor . Det är inte en vanlig polyeder eftersom vissa hörn har fyra ytor och andra har fem. Det är en dodekaeder , en av de åtta deltaedrarna (konvexa polyedrar med liksidiga triangelytor), och är den 84:e Johnson solida (icke- likformiga konvexa polyedrar med regelbundna ytor). Det kan ses som ett kvadratiskt antiprisma där båda kvadraterna ersätts med två liksidiga trianglar.

Den snubbade disfenoiden är också vertexfiguren för det isogonala 13-5 stegs prismat, en polykoron som är konstruerad från en 13-13 duoprism genom att välja en vertex på en tridecagon , sedan välja den 5:e vertexen på nästa tridecagon, gör det tills du når originalet tridecagon. Den kan dock inte göras enhetlig, eftersom snub-disfenoiden inte har någon avgränsad sfär .

Historia och namngivning

Denna form kallades en siamesisk dodekaeder i tidningen av Hans Freudenthal och BL van der Waerden (1947) som först beskrev uppsättningen av åtta konvexa deltaedrar . Dodekadeltaedernamnet gavs till samma form av Bernal (1964) , med hänvisning till det faktum att det är en 12-sidig deltaeder. Det finns andra enkla dodekaedrar , såsom den hexagonala bipyramiden , men detta är den enda som kan realiseras med liksidiga ansikten. Bernal var intresserad av formerna av hål kvar i oregelbundna tätpackade arrangemang av sfärer, så han använde en restriktiv definition av deltaedrar, där en deltaeder är en konvex polyeder med triangulära ytor som kan bildas av mitten av en samling kongruenta sfärer, vars tangenser representerar polyederkanter, och sådana att det inte finns utrymme att packa en annan sfär inuti buren skapad av detta system av sfärer. Denna restriktiva definition tillåter inte den triangulära bipyramiden (som bildar två tetraedriska hål snarare än ett enda hål), den femkantiga bipyramiden (eftersom sfärerna för dess spetsar tränger in i varandra, så den kan inte förekomma i sfärförpackningar) och icosahedron (eftersom den har inre utrymme för en annan sfär). Bernal skriver att snub-disfenoiden är "en mycket vanlig koordination för kalciumjonen i kristallografi ". I koordinationsgeometri är det vanligtvis känt som den trigonala dodekaedern eller helt enkelt som dodekaedern.

Det snubbade disfenoidnamnet kommer från Norman Johnsons klassificering 1966 av Johnson solids , konvexa polyedrar vars ansikten alla är regelbundna. Det finns först i en serie av polyedrar med axiell symmetri, så det kan också ges namnet digonal gyrobianticupola .

Egenskaper

Snubbdisfenoiden är 4-ansluten , vilket innebär att det krävs att fyra hörn tas bort för att koppla bort de återstående hörnen. Det är en av endast fyra 4-anslutna enkla vältäckta polyedrar, vilket betyder att alla de maximalt oberoende uppsättningarna av dess hörn har samma storlek. De andra tre polyedrarna med denna egenskap är den regelbundna oktaedern , den femkantiga bipyramiden och en oregelbunden polyeder med 12 hörn och 20 triangulära ytor.

Den snubbade disfenoiden har samma symmetri som en tetragonal disfenoid : den har en axel med 180° rotationssymmetri genom mittpunkterna på sina två motsatta kanter, två vinkelräta plan av reflektionssymmetri genom denna axel, och fyra ytterligare symmetrioperationer som ges av en reflektionsvinkelrät till axeln följt av ett kvartsvarv och eventuellt ytterligare en reflektion parallellt med axeln. Det vill säga, den har D2d _{, .} antiprismatisk symmetri en symmetrigrupp av ordning 8

Sfärer som är centrerade vid hörnen av snub-disfenoiden bildar ett kluster som, enligt numeriska experiment, har minsta möjliga Lennard-Jones-potential bland alla åttasfäriska kluster.

Upp till symmetrier och parallell översättning har snub-disfenoiden fem typer av enkla (icke-självkorsande) slutna geodesiker . Dessa är banor på polyederns yta som undviker hörnen och lokalt ser ut som en kortaste väg: de följer räta linjesegment över varje yta av polyedern som de korsar, och när de korsar en kant på polyederen bildar de komplementära vinklar på de två incidenterna är vända mot kanten. Intuitivt skulle man kunna sträcka ett gummiband runt polyedern längs denna väg och det skulle stanna på plats: det finns inget sätt att lokalt ändra banan och göra den kortare. Till exempel korsar en typ av geodetisk de två motsatta kanterna av snub-disfenoiden vid deras mittpunkter (där symmetriaxeln lämnar polytopen) med en vinkel på π /3. En andra typ av geodetik passerar nära skärningspunkten mellan snub-disfenoiden och planet som vinkelrätt delar symmetriaxeln ( polyederns ekvator ) och korsar kanterna på åtta trianglar i vinklar som växlar mellan π /2 och π /6. Att flytta en geodetik på polyederns yta med en liten mängd (tillräckligt liten för att förskjutningen inte får den att korsa några hörn) bevarar egenskapen att vara en geodetisk och bevarar dess längd, så båda dessa exempel har förskjutna versioner av samma typ som är mindre symmetriskt placerade. Längden på de fem enkla slutna geodetikerna på en snub-disfenoid med kanter i enhetslängd är

$2{\sqrt {3}}\approx 3.464$ (för ekvatorial geodetik), ${\displaystyle {\sqrt {13}}\approx 3.606} stil$ , ${\displaystyle$ (för geodetik genom mittpunkterna på motsatta kanter), $2{\sqrt {7}}\approx 5.292$ och ${\displaystyle {\sqrt {19}}\59} 4.359$ .

Förutom tetraedern, som har oändligt många typer av enkla slutna geodesiker, har snub-disfenoiden de flesta typerna av geodesik av alla deltaeder.

Konstruktion

Den snubbade disphenoiden är konstruerad, som dess namn antyder, som den snubpolyhedron som bildas från en tetragonal disphenoid , en lägre symmetriform av en regelbunden tetrahedron .

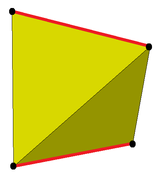
Disfenoid	Snub disfenoid

Snubbningsoperationen producerar ett enda cykliskt band av trianglar som separerar två motsatta kanter (röda i figuren) och deras intilliggande trianglar. De snubbade antiprismorna är analoga med att ha ett enda cykliskt band av trianglar, men i de snubbade antiprismorna separerar dessa band två motsatta ytor och deras intilliggande trianglar snarare än två motsatta kanter.

Den snubbade disfenoiden kan också konstrueras från det kvadratiska antiprismat genom att ersätta de två fyrkantiga ytorna med par av liksidiga trianglar. Det är dock ett av de elementära Johnson-fastämnena som inte uppstår från "klipp och klistra"-manipulationer av de platonska och arkimedeiska fasta ämnen.

En fysisk modell av snub-disfenoiden kan bildas genom att vika ett nät bildat av 12 liksidiga trianglar (en 12-diamant), som visas. Ett alternativt nät som föreslagits av John Montroll har färre konkava hörn på sin gräns, vilket gör det bekvämare för origamikonstruktion .

kartesiska koordinater

Låt $q\approx 0,16902$ vara den positiva reella roten av det kubiska polynomet

$2x^{3}+11x^{2}+4x-1.$

Dessutom låt

$r={\sqrt {q}}\approx 0,41112,$

$s={\sqrt {\}{qrt {\}{1-q 2q}}}\approx 1,56786,$

och

$t=2rs={\sqrt {2-2q}}\approx 1.28917.$

De åtta hörnen av snub-disfenoiden kan då ges kartesiska koordinater

$(\pm t,r,0),\,(0,-r,\pm t),$

$(\pm 1,-s,0),\,(0,s,\pm 1).$

Eftersom denna konstruktion involverar lösningen på en kubisk ekvation, kan snub-disfenoiden inte konstrueras med en kompass och rätsida, till skillnad från de andra sju deltaedrarna.

Med dessa koordinater är det möjligt att beräkna volymen av en snub-disfenoid med kantlängd a som ${\displaystyle \xi a^{3}} ,$ där $\xi \approx 0,85949$ är positiv rot av polynomet

$5832x^{6}-1377x^{4}-2160x^{2}-4.$

Den exakta formen av $\xi$ kan uttryckas som,

$\xi ={\frac {1}{6{\sqrt {6}}}}{\sqrt {17+ {\sqrt[{3}]{155249-28848i{\sqrt {237}}}}+{\sqrt[{3}]{155249+28848i{\sqrt {237}}}}}},$

$\xi ={\frac {1}{6{\sqrt {6}}}}{\sqrt {17 +2{\sqrt {6049}}\cos \left({\frac {1}{3}}\tan ^{-1}\left({\frac {28848{\sqrt {237}}}{155249} }\eller hur)}},$

där $i$ är den imaginära enheten.

Besläktade polyedrar

En annan konstruktion av snub-disfenoiden är som en digonal gyrobianticupola . Den har samma topologi och symmetri, men utan liksidiga trianglar. Den har 4 hörn i en kvadrat på ett mittplan som två antikupoler fästa med rotationssymmetri. Dess dubbla har rätvinkliga femhörningar och kan självbilda rymden.

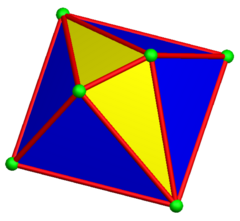Digonal antikupola

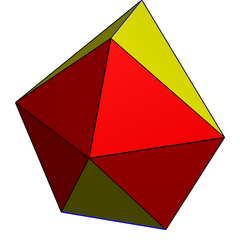Digonal gyrobianticupola

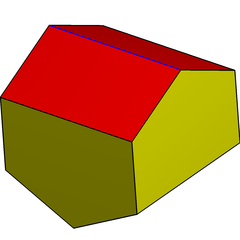(Dubbel) långsträckt gyrobifastigium

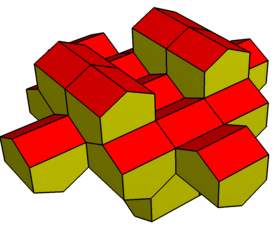Partiell tessellation

externa länkar

• Weisstein, Eric W. "Snub disphenoid" . MathWorld .