Hexaeder
En hexahedron (plural: hexahedra eller hexahedrons ) eller sexahedron (plural: sexahedra eller sexahedrons ) är vilken polyeder som helst med sex ansikten . En kub , till exempel, är en vanlig hexaeder med alla dess ytor kvadratiska och tre kvadrater runt varje vertex .
Det finns sju topologiskt distinkta konvexa hexaedrar, varav en finns i två spegelbildsformer. Det finns tre topologiskt distinkta konkava hexaedrar. Två polyedrar är "topologiskt distinkta" om de har i sig olika arrangemang av ytor och hörn, så att det är omöjligt att förvränga den ena till den andra helt enkelt genom att ändra längden på kanterna eller vinklarna mellan kanter eller ytor.
Konvex, kuboid
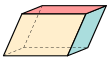
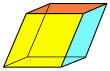
| Fyrkantigt vänd hexaeder ( kuboid ) 6 ytor, 12 kanter, 8 hörn | ||||||
|---|---|---|---|---|---|---|

|

|

|

|

|
|
|
|
Kub ( fyrkantig ) |
Rektangulär kubform (tre par rektanglar ) |
Trigonal trapezoeder (kongruent rombi ) |
Trigonal trapezoeder (kongruenta fyrhörningar ) |
Quadrilateral frustum (spets-trunkerad fyrkantig pyramid ) |
Parallelepiped (tre par parallellogram ) |
Rhombohedron (tre par rombi ) |
|
Åh , [4,3], (*432) ordning 48 |
D 2h , [2,2], (*222) ordning 8 |
D 3 d , [2 + ,6], (2*3) order 12 |
D 3 , [2,3] + , (223) ordning 6 |
C 4v , [4], (*44) order 8 |
C i , [2 + ,2 + ], (×) ordning 2 |
|
Konvexa, andra
| Konvex | |||||
|---|---|---|---|---|---|

|
 
|

|

|

|
|
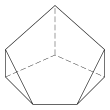
| Triangulär bipyramid | Tetragonal antikil. Chiral – finns i "vänsterhänta" och "högerhänta" spegelbilder. | Pentagonal pyramid | |||
|
3 6 Ytor 9 E, 5 V |
4.4.3.3.3.3 Ytor 10 E, 6 V |
4.4.4.4.3.3 Ytor 11 E, 7 V |
5.3 5 Ytor 10 E, 6 V |
5.4.4.3.3.3 Ytor 11 E, 7 V |
5.5.4.4.3.3 Ytor 12 E, 8 V |
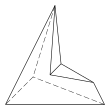
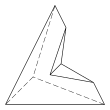
Konkav
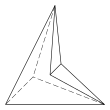
Det finns ytterligare tre topologiskt distinkta hexaedrar som endast kan realiseras som konkava figurer:
| Konkav | ||
|---|---|---|
|
|
|
|
4.4.3.3.3.3 Ytor 10 E, 6 V |
5.5.3.3.3.3 Ytor 11 E, 7 V |
6.6.3.3.3.3 Ytor 12 E, 8 V |
En digonal antiprisma kan betraktas som en degenererad form av hexaeder, med två motstående digonala ytor och fyra triangulära ytor. Emellertid ignoreras digoner vanligtvis i definitionen av icke-sfäriska polyedrar, och det här fallet anses ofta helt enkelt vara en tetraeder och de fyra återstående triangulära ytorna anses utgöra hela soliden.
Se även
externa länkar
- Polyhedra med 4-7 ansikten av Steven Dutch