Bitruncated kubisk honungskaka

Bitruncated kubisk honungskaka

Typ	Enhetlig honungskaka
Schläfli symbol	2t{4,3,4} t _1,2 {4,3,4}
Coxeter-Dynkin diagram
Celltyp	( 4.6.6 )
Ansiktstyper	kvadratisk {4} sexkant {6}
Kantfigur	likbent triangel {3}
Vertex figur	( tetragonal disfenoid )
Rymdgrupp Fibrifold notation Coxeter notation	Jag är 3 m (229) 8 ^o :2 [[4,3,4]]
Coxeter grupp	${\tilde {C}}_{3}$ , [4,3,4]
Dubbel	Oblat tetrahedrill Disfenoid tetraedrisk bikakecell:
Egenskaper	isogonal , isotoxal , isokorisk

Den bitruncerade kubiska bikakan som visas här i förhållande till en kubisk bikaka

Den bitrunkerade kubiska bikakan är en rymdfyllande tessellation (eller honeycomb ) i euklidisk 3-rymd som består av trunkerade oktaedrar (eller, på motsvarande sätt, bitrunkerade kuber). Den har 4 stympade oktaedrar runt varje vertex. Består helt och hållet av trunkerade oktaedrar , är den celltransitiv . Den är också kanttransitiv , med 2 hexagoner och en kvadrat på varje kant, och vertextransitiv . Det är en av 28 enhetliga honungskakor .

John Horton Conway kallar denna honeycomb för en trunkerad octahedrille i sin Architectonic and catoptric tessellation list, med dess dubbla kallad oblate tetrahedrille , även kallad en disphenoid tetrahedral honeycomb . Även om en vanlig tetraeder inte kan tessellate rymden ensam, har denna dual identiska disfenoida tetraederceller med likbenta triangelytor .

Geometri

Det kan realiseras som Voronoi-tesselationen av det kroppscentrerade kubiska gittret. Lord Kelvin förmodade att en variant av den bitrunkerade kubiska bikakan (med böjda ytor och kanter, men samma kombinatoriska struktur) var det optimala såpbubbelskummet. Men ett antal mindre symmetriska strukturer har senare visat sig vara mer effektiva skum av såpbubblor, bland vilka Weaire- Phelan-strukturen verkar vara den bästa.

Bikakan representerar permutohedron- tesselationen för 3-mellanrum. Koordinaterna för hörn för en oktaeder representerar ett hyperplan av heltal i 4-rymden, specifikt permutationer av (1,2,3,4). Tessellationen bildas av översatta kopior inom hyperplanet.

Tessellationen är den högsta tessellationen av parallelloeder i 3-rymden.

Projektioner

Den bitrunkerade kubiska bikakan kan projiceras ortogonalt in i det euklidiska planet med olika symmetriarrangemang. Den högsta (hexagonala) symmetriformen projicerar ut i en olikformig rhombitrihexagonal plattsättning . En kvadratisk symmetriprojektion bildar två överlappande trunkerade fyrkantiga plattor , som kombineras som en avfasad kvadratisk plattsättning .

Ortogonala projektioner
Symmetri	p6m (*632)	p4m (*442)	pmm (*2222)
Solid
ram

Symmetri

Hönsfiguren för denna bikaka är en disfenoid tetraeder , och det är också Goursat-tetraedern ( grunddomän ) för ${\tilde {A}}_{3}$ Coxeter-gruppen . Denna bikaka har fyra enhetliga konstruktioner, med de trunkerade oktaedriska cellerna som har olika Coxeter-grupper och Wythoff-konstruktioner . Dessa enhetliga symmetrier kan representeras genom att färga olika celler i varje konstruktion.

Fem enhetliga färger per cell
Rymdgrupp	Jag är 3 m (229)	Pm 3 m (221)	Fm 3 m (225)	F 4 3 m (216)	Fd 3 m (227)
Fibrifold	8 ^o :2	4 ⁻ :2	2 ⁻ :2	1 ^o :2	2+ ^: 2
Coxeter grupp	${\tilde {C}}_{3}$ ×2 [[4,3,4]] =[4[3 ^[4] ]] =	${\tilde {C}}_{3}$ [4,3,4] =[2[3 ^[4] ]] =	${\tilde {B}}_{3}$ [4,3 ^1,1 ] =<[3 ^[4] ]> =	${\tilde {A}}_{3}$ [3 ^[4] ]	${\tilde {A}}_{3}$ ×2 [[3 ^[4] ]] =[[3 ^[4] ]]
Coxeter diagram
trunkerade oktaedrar	1	1:1 :	2:1: 1 ::	1:1:1:1 : : :	1:1 :
Vertex figur
Vertex figur symmetri	[2 ⁺ ,4] (ordning 8)	[2] (ordning 4)	[ ] (ordning 2)	[ ] ⁺ (ordning 1)	[2] ⁺ (ordning 2)
Bild färgad av cell

Besläktade polyedrar och honungskakor

Den vanliga sneda apeiroedern {6,4|4} innehåller hexagonerna i denna bikaka.

[4,3,4], , Coxeter-gruppen genererar 15 permutationer av enhetliga tesseller, 9 med distinkt geometri inklusive den alternerade kubiska bikakan. Den expanderade kubiska bikakan (även känd som den runcinerade tesseractic honeycomb) är geometriskt identisk med den kubiska bikakan.

C3 honungskakor
Rymdgrupp _	Fibrifold	Utökad symmetri	Utökat diagram	Beställa	Honeycombs
Pm 3 m (221)	4 ⁻ :2	[4,3,4]		×1	₁ , ₂ , ₃ , ₄ , ₅ , ₆
Fm 3 m (225)	2 ⁻ :2	[1 ⁺ ,4,3,4] ↔ [4,3 ^1,1 ]	↔	Halv	₇ , ₁₁ , ₁₂ , ₁₃
I 4 3m (217)	4 ^o :2	[[(4,3,4,2 ⁺ )]]		Hälften × 2	₍₇₎ ,
Fd 3 m (227)	2+ ^: 2	[[1 ⁺ ,4,3,4,1 ⁺ ]] ↔ [[3 ^[4] ]]	↔	Kvartal × 2	₁₀ ,
Jag är 3 m (229)	8 ^o :2	[[4,3,4]]		×2	₍₁₎ , ₈ , ₉

[4,3 ^1,1 ], , Coxeter-gruppen genererar 9 permutationer av enhetliga tesseller, 4 med distinkt geometri inklusive den alternerade kubiska bikakan.

B3 honungskakor
Rymdgrupp _	Fibrifold	Utökad symmetri	Utökat diagram	Beställa	Honeycombs
Fm 3 m (225)	2 ⁻ :2	[4,3 ^1,1 ] ↔ [4,3,4,1 ⁺ ]	↔	×1	₁ , ₂ , ₃ , ₄
Fm 3 m (225)	2 ⁻ :2	<[1 ⁺ ,4,3 ^1,1 ]> ↔ <[3 ^[4] ]>	↔	×2	₍₁₎ , ₍₃₎
Pm 3 m (221)	4 ⁻ :2	<[4,3 ^1,1 ]>		×2	₅ , ₆ , ₇ , ₍₆₎ , ₉ , ₁₀ , ₁₁

Denna bikaka är en av fem distinkta enhetliga bikakor som konstruerats av ${\tilde {A}}_{3}$ Coxeter-gruppen . Symmetrin kan multipliceras med symmetrin hos ringar i Coxeter–Dynkin-diagrammen :

A3 honungskakor
Rymdgrupp _	Fibrifold	Kvadratisk symmetri	Utökad symmetri	Utökat diagram	Utökad grupp	Bikakediagram
F 4 3 m (216)	1 ^o :2	a1	[3 ^[4] ]		${\tilde {A}}_{3}$	(Ingen)
Fm 3 m (225)	2 ⁻ :2	d2	<[3 ^[4] ]> ↔ [4,3 ^1,1 ]	↔	${\tilde {A}}_{3}$ ×2 ₁ ↔ ${\tilde {B}}_{3}$	₁ , ₂
Fd 3 m (227)	2+ ^: 2	g2	[[3 ^[4] ]] eller [2 ⁺ [3 ^[4] ]]	↔	${\tilde {A}}_{3}$ ×2 ₂	₃
Pm 3 m (221)	4 ⁻ :2	d4	<2[3 ^[4] ]> ↔ [4,3,4]	↔	${\tilde {A}}_{3}$ ×4 ₁ ↔ ${\tilde {C}}_{3}$	₄
I 3 (204)	8 ^−o	r8	[4[3 ^[4] ]] ⁺ ↔ [[4,3 ⁺ ,4]]	↔	½ ${\tilde {A}}_{3}$ ×8 ↔ ½ ${\tilde {C}}_{3}$ ×2	_(*)
Jag är 3 m (229)	8 ^o :2	r8	[4[3 ^[4] ]] ↔ [[4,3,4]]	↔	${\tilde {A}}_{3}$ ×8 ↔ ${\tilde {C}}_{3}$ ×2	₅

Omväxlande form

Alternerad bitruncated kubisk honungskaka
Typ	Konvex honungskaka
Schläfli symbol	2s{4,3,4} 2s{4,3 ^1,1 } sr{3 ^[4] }
Coxeter diagram	= = =
Celler	tetraeder ikosaeder
Vertex figur
Coxeter grupp	[[4,3 ⁺ ,4]], ${\tilde {C}}_{3}$
Dubbel	Tio diamanter honeycomb Cell:
Egenskaper	vertex-transitiv

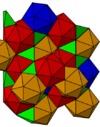
Denna bikaka kan alterneras och skapa pyritoedriska icosaedrar från de trunkerade oktaedrarna med disfenoida tetraedriska celler skapade i mellanrummen. Det finns tre konstruktioner från tre relaterade Coxeter-Dynkin-diagram : , , och . Dessa har symmetri [4,3 ⁺ ,4], [4,(3 ^1,1 ) ^{+ ]} respektive [3 ^[4] ] ^{+ .} Den första och sista symmetrin kan dubblas till [[4,3 ⁺ ,4]] och [[3 ^[4] ]] ⁺ .

Den dubbla bikakan är gjord av celler som kallas tio-av-diamanter dekaedrar .

Fem enhetliga färger
Rymdgrupp	I 3 (204)	15:00 (200 )	Fm 3 (202)	Fd 3 (203)	F23 (196)
Fibrifold	8 ^−o	4 ⁻	2 ⁻	2 ^o+	1 ^o
Coxeter grupp	[[4,3 ⁺ ,4]]	[4,3 ⁺ ,4]	[4,(3 ^1,1 ) ⁺ ]	[[3 ^[4] ]] ⁺	[3 ^[4] ] ⁺
Coxeter diagram
Beställa	dubbel	full	halv	kvartsdubbel _	fjärdedel
Bild färgad av celler

Denna bikaka är representerad i boratomerna i den a-romboedriska kristallen . Mitten av icosahedran är belägna vid fcc-positionerna av gittret.

Besläktade polytoper

Olikformiga varianter med [4,3,4] symmetri och två typer av trunkerade oktaedrar kan fördubblas genom att placera de två typerna av trunkerade oktaedrar för att producera en olikformig bikaka med trunkerade oktaedrar och hexagonala prismor (som ditrigonala trapetsor). Dess vertexfigur är en C _2v- symmetrisk triangulär bipyramid .

Denna bikaka kan sedan alterneras för att producera en annan ojämn bikaka med pyritoedriska icosahedra , oktaedrar (som triangulära antiprismor) och tetraedrar (som sfenoider). Dess vertexfigur har C _2v- symmetri och består av 2 pentagoner , 4 rektanglar , 4 likbenta trianglar (delade i två uppsättningar av 2) och 4 skalenliga trianglar .

Se även

Anteckningar

John H. Conway , Heidi Burgiel, Chaim Goodman-Strauss , (2008) The Symmetries of Things , ISBN 978-1-56881-220-5 (Kapitel 21, Namngivning av arkimediska och katalanska polyedrar och plattsättningar, Architectonic and Catoptrics, p tess 292-298, inkluderar alla icke-prismatiska former)
George Olshevsky, Uniform Panoploid Tetracombs , Manuscript (2006) (Komplett lista med 11 konvexa enhetliga plattor, 28 konvexa enhetliga honeycombs och 143 konvexa enhetliga tetracombs)
Branko Grünbaum , Enhetlig plattsättning av 3-utrymmen. Geombinatorics 4 (1994), 49-56.
Kaleidoscopes: Selected Writings of HSM Coxeter , redigerad av F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [2]
- (Paper 22 ) HSM Coxeter, Regular and Semi Regular Polytopes I , [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Enhetliga utrymmesfyllningar)
A. Andreini , Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative ( Om polyedrarnas regelbundna och halvregelbundna nät och på motsvarande korrelativa nät), Mem. Società Italiana della Scienze, Ser.3, 14 (1905) 75–129.
Klitzing, Richard. "3D Euklidiska Honeycombs o4x3x4o - batch - O16" .
Uniforma honungskakor i 3-utrymme: 05-batch
Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design . Dover Publications, Inc. ISBN 0-486-23729-X .

externa länkar

Weisstein, Eric W. "Rymdsfyllande polyeder" . MathWorld .