hp-FEM

hp-FEM är en generell version av finita elementmetoden (FEM), en numerisk metod för att lösa partiella differentialekvationer baserad på bitvis-polynomapproximationer som använder element av variabel storlek ( h) och polynomgrad (p) . Ursprunget till hp-FEM går tillbaka till Barna A. Szabós och Ivo Babuškas banbrytande arbete som upptäckte att den finita elementmetoden konvergerar exponentiellt snabbt när nätet förfinas med hjälp av en lämplig kombination av h-förfinningar (delar av element i mindre) och p-förfinningar (ökning av deras polynomgrad). Den exponentiella konvergensen gör metoden mycket attraktiv jämfört med de flesta andra finita elementmetoder, som endast konvergerar med en algebraisk hastighet. Den exponentiella konvergensen av hp-FEM förutspåddes inte bara teoretiskt, utan observerades också av många oberoende forskare.

Skillnader från standard FEM

hp-FEM skiljer sig från standard (lägsta ordningens) FEM i många aspekter.

Val av högre ordningens formfunktioner ^{[ exempel behövs ]} : Polynomen i högre grad i element kan genereras med hjälp av olika uppsättningar av formfunktioner. Valet av en sådan uppsättning kan dramatiskt påverka konditioneringen av styvhetsmatrisen, och i sin tur hela lösningsprocessen. Detta problem dokumenterades först av Babuska et al.
Automatisk hp-adaptivitet : I hp-FEM kan ett element hp-förfinas på många olika sätt, såsom: Öka dess polynomgrad utan att dela upp det i rymden, eller dela in elementet geometriskt, där olika polynomgrader kan tillämpas på delelement. Antalet elementförfiningskandidater når lätt 100 i två dimensioner och 1000 i tre dimensioner. Ett nummer som indikerar storleken på felet i ett element är inte tillräckligt för att styra automatisk hp-adaptivitet (i motsats till adaptivitet i standard FEM). Andra tekniker som referenslösningar eller analytiska överväganden måste användas för att få mer information om felformen i varje element.
Förhållande mellan montering och lösning CPU-tider : I standard FEM monteras styvhetsmatrisen vanligtvis snabbt men den är ganska stor. Vanligtvis förbrukar lösningen av det diskreta problemet den största delen av den totala beräkningstiden. Däremot är styvhetsmatriserna i hp-FEM vanligtvis mycket mindre, men (för samma matrisstorlek) tar deras sammansättning längre tid än i standard-FEM. Detta beror främst på beräkningskostnaden för numerisk kvadratur, som måste ha högre precision och därför vara av högre ordning, jämfört med standard FEM för att dra fördel av de snabbare konvergenshastigheterna.
Analytiska utmaningar : hp-FEM anses generellt vara svårare att förstå ur analytisk synvinkel än standard FEM. ^{[ enligt vem? ]} Detta gäller många tekniker, såsom de diskreta maximala principerna (DMP) för elliptiska problem. Dessa resultat anger att, vanligtvis med vissa begränsande antaganden om nätet, följer den bitvis-polynomiska FEM-approximationen analoga maximiprinciper som den underliggande elliptiska PDE. Sådana resultat är mycket viktiga eftersom de garanterar att approximationen förblir fysiskt tillåten, vilket inte lämnar någon möjlighet att beräkna en negativ densitet, negativ koncentration eller negativ absolut temperatur. DMP är ganska välkända för lägsta ordningens FEM men helt okända för hp-FEM i två eller flera dimensioner. Den första DMP i en rumslig dimension formulerades nyligen.
Programmeringsutmaningar : Det är mycket svårare att implementera en hp-FEM-lösare än standard FEM-kod. De många problem som måste övervinnas inkluderar (men är inte begränsade till): högre ordningens kvadraturformler, högre ordningens formfunktioner, anslutnings- och orienteringsinformation som relaterar formfunktioner på referensdomänen med basfunktioner i den fysiska domänen, etc.

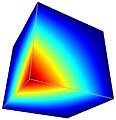
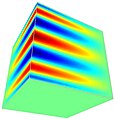
Fichera-problemet

Fichera-problemet (även kallat Fichera-hörnproblemet) är ett standardproblem för adaptiva FEM-koder. Man kan använda den för att visa den dramatiska skillnaden i prestanda för standard FEM och hp-FEM. Problemgeometrin är en kub med saknat hörn. Den exakta lösningen har en singulär gradient (en analogi av oändlig stress) i centrum. Kunskapen om den exakta lösningen gör det möjligt att beräkna approximationsfelet exakt och därmed jämföra olika numeriska metoder. Som illustration löstes problemet med tre olika versioner av adaptiv FEM: med linjära element, kvadratiska element och hp-FEM.

Fichera problem: singularis gradient.
Fichera-problem: konvergensjämförelse.

Konvergensgraferna visar approximationsfelet som en funktion av antalet frihetsgrader (DOF). DOF hänvisar till okända parametrar som behövs för att definiera approximationen, och antalet DOF är lika med storleken på styvhetsmatrisen. Läsaren kan se i graferna att konvergensen för hp-FEM är mycket snabbare än konvergensen för båda andra metoderna. Prestandagapet är tillräckligt stort för att den linjära FEM kanske inte konvergerar alls (inom rimlig tid) och den kvadratiska FEM skulle behöva hundratusentals eller kanske miljoner DOF för att nå den noggrannhet som hp-FEM uppnådde med cirka 17 000 DOF. Att få mycket exakta resultat med relativt få frihetsgrader är den främsta styrkan med hp-FEM.

Effektivitet av hp-FEM

Släta funktioner kan approximeras mycket mer effektivt med hjälp av stora element av hög ordning än små bitvis linjära. Detta illustreras i figuren nedan, där en endimensionell Poisson-ekvation med noll Dirichlet-randvillkor löses på två olika maskor. Den exakta lösningen är sinusfunktionen.

Vänster: nät bestående av två linjära element.
Höger: nät bestående av ett kvadratiskt element.

Medan antalet okända är detsamma i båda fallen (1 DOF), är felen i motsvarande norm 0,68 respektive 0,20. Detta betyder att den kvadratiska approximationen var ungefär 3,5 gånger effektivare än den bitvis linjära. När vi går ett steg längre och jämför (a) fyra linjära element med (b) ett kvartselement (p=4), så kommer båda diskreta problemen att ha tre DOF men den kvartiska approximationen kommer att vara ungefär 40 gånger effektivare.

Tvärtom kan små lågordnade element fånga småskaliga egenskaper som singulariteter mycket bättre än stora högordningselement. hp-FEM bygger på en optimal kombination av dessa två tillvägagångssätt vilket leder till exponentiell konvergens. Observera att denna exponentiella konvergens uttrycks i felaxel kontra frihetsgrader. För verkliga applikationer överväger vi vanligtvis beräkningstid som krävs för att nå samma noggrannhetsnivå. För denna prestandaindikator kan h- och hp-förfining ge liknande resultat, t.ex. se den slutliga figuren på (WebArchive-länk ). Så snart det är svårare att programmera och parallellisera hp-FEM jämfört med h-FEM, kan konvergensexcellensen av hp-förfining bli opraktisk.

Hp-anpassning

Vissa FEM-platser beskriver hp-adaptivitet som en kombination av h-adaptivitet (dela upp element i rymden samtidigt som de håller sin polynomgrad fixerad) och p-adaptivitet (som bara ökar deras polynomgrad) [ ^{citat behövs ]} . Detta är inte helt korrekt, eftersom hp-adaptivitet skiljer sig väsentligt från både h- och p-adaptivitet då hp-förfining av ett element kan göras på många olika sätt. Förutom en p-förfining kan elementet delas in i rymden (som i h-adaptivitet), men det finns många kombinationer för polynomgraderna på underelementen. Detta illustreras i bilden till höger. Till exempel, om ett triangulärt eller fyrsidigt element är uppdelat i fyra delelement där polynomgraderna tillåts variera med högst två, så ger detta 3^4 = 81 förfiningskandidater (inte med tanke på polynomiellt anisotropa kandidater). Analogt, uppdelning av en hexaeder i åtta delelement och variation av deras polynomgrader med högst två ger 3^8 = 6 561 förfiningskandidater. Standard FEM-feluppskattningar som ger ett konstant tal per element är inte tillräckligt för att styra automatisk hp-adaptivitet.

Formfunktioner av högre ordning

I standard FEM arbetar man bara med formfunktioner som är förknippade med rutnätshörn (de så kallade vertexfunktionerna) . Däremot, när man använder hp-FEM, betraktar man dessutom kantfunktioner (associerade med elementkanter), ansiktsfunktioner (motsvarande elementytor – endast 3D) och bubbelfunktioner (polynom av högre ordning som försvinner på elementgränser). Följande bilder visar dessa funktioner (begränsade till ett enda element):

Vertex funktion.
Kantfunktion.
Ansiktsfunktion.
Bubbelfunktion.

Observera: alla dessa funktioner är definierade i hela elementets inre.

Öppen källkod hp-FEM-koder

Deal.II : Deal.II är ett gratis bibliotek med öppen källkod för att lösa partiella differentialekvationer med finita elementmetoden.
Koncept : C/C++ hp-FEM/DGFEM/BEM-bibliotek för elliptiska ekvationer utvecklat vid SAM, ETH Zürich (Schweiz) och i gruppen av K. Schmidt vid TU Berlin (Tyskland).
2dhp90, 3dhp90: Fortran kodar för elliptiska problem och Maxwells ekvationer utvecklade av L. Demkowicz vid ICES, UT Austin.
PHAML: The Parallel Hierarchical Adaptive MultiLevel Project. Finita element-mjukvara utvecklad vid National Institute for Standards and Technology, USA, för numerisk lösning av 2D elliptiska partiella differentialekvationer på parallella datorer med distribuerat minne och flerkärniga datorer med adaptiv mesh-förfining och multigrid-lösningstekniker.
Hermes Project : C/C++/Python-bibliotek för snabb prototypframställning av rymd- och rumtidsanpassningsbara hp-FEM-lösare för ett stort antal PDE:er och multifysiska PDE-system, utvecklat av hp-FEM-gruppen vid University of Nevada, Reno ( USA), Institute of Thermo-mechanics, Prag (Tjeckien), och University of West Bohemia i Pilsen (Tjeckien) – med Agros2D- ingenjörsmjukvaran byggd ovanpå Hermes-biblioteket.
PHG : PHG är en verktygslåda för att utveckla parallella adaptiva finita elementprogram. Den är lämplig för h-, p- och hp-fem. PHG är för närvarande under aktiv utveckling vid State Key Laboratory of Scientific and Engineering Computing, Institute of Computational Mathematics and Scientific/Engineering Computing of Chinese Academy of Sciences (LSEC, CAS, Kina). PHG hanterar överensstämmande tetraedriska nät och använder bisektion för adaptiv lokal nätförfining och MPI för meddelandeöverföring. PHG har en objektorienterad design som döljer parallelliseringsdetaljer och tillhandahåller vanliga operationer på maskor och finita elementfunktioner på ett abstrakt sätt, vilket gör att användarna kan koncentrera sig på sina numeriska algoritmer.
MoFEM är en finita elementanalyskod skräddarsydd för lösning av multifysiska problem med godtyckliga nivåer av approximation, olika nivåer av mesh-förfining och optimerad för högpresterande beräkningar. Den är utformad för att kunna hantera komplexitet relaterade till en heterogen ordning av approximationer för L2, H1, H-div och H-curl utrymmen
Sparselizard är ett multifysiskt, hp-adaptivt, användarvänligt, öppen källkod C++ finita element-bibliotek som för närvarande utvecklas vid Tammerfors universitet, Finland. Den kombinerar 3D-tetraedrar och 2D-triangel/fyrkant-konform adaptiv mesh-förfining med hierarkiska H1- och H-curl-funktionsutrymmen i godtycklig ordning för allmän statisk och transient hp-FEM.

Kommersiell programvara för hp-FEM

StressCheck är ett analysverktyg med finita element med hp-kapacitet inriktat på detaljerad strukturanalys.