Hydrodynamik med utjämnad partikel

Schematisk vy av en SPH-falsning

Flöda runt cylindern med fri yta modellerad med SPH. Se för liknande simuleringar.

Smoothed-particle hydrodynamics ( SPH ) är en beräkningsmetod som används för att simulera mekaniken i kontinuummedier, såsom fast mekanik och vätskeflöden . Det utvecklades av Gingold och Monaghan och Lucy 1977, ursprungligen för astrofysiska problem. Det har använts i många områden av forskning, inklusive astrofysik , ballistik , vulkanologi och oceanografi . Det är en meshfri lagrangisk metod (där koordinaterna rör sig med vätskan), och metodens upplösning kan enkelt justeras med hänsyn till variabler som densitet .

Metod

Fördelar

• Till sin konstruktion är SPH en nätfri metod , vilket gör den idealisk för att simulera problem som domineras av komplex gränsdynamik, som fria ytflöden eller stora gränsförskjutningar.
• Avsaknaden av ett mesh förenklar avsevärt modellimplementeringen och dess parallellisering, även för arkitekturer med många kärnor .

• SPH kan enkelt utvidgas till en mängd olika områden och hybridiseras med några andra modeller, som diskuteras i Modeling Physics .
• Som diskuterats i avsnittet om svagt komprimerbar SPH , har metoden stora bevarandeegenskaper.
• Beräkningskostnaden för SPH-simuleringar per antal partiklar är betydligt mindre än kostnaden för rutnätsbaserade simuleringar per antal celler när måtten av intresse är relaterad till vätskedensitet (t.ex. sannolikhetstäthetsfunktionen för densitetsfluktuationer ) . Så är fallet eftersom i SPH läggs resolutionen där saken ligger.

Begränsningar

• Att sätta gränsvillkor i SPH såsom in- och utlopp och väggar är svårare än med rutnätsbaserade metoder. Faktum är att det har konstaterats att "behandlingen av randvillkor förvisso är en av de svåraste tekniska punkterna med SPH-metoden". Denna utmaning beror delvis på att i SPH förändras partiklarna nära gränsen med tiden. Ändå finns vägggränsvillkor för SPH tillgängliga
• Beräkningskostnaden för SPH-simuleringar per antal partiklar är betydligt större än kostnaden för rutnätsbaserade simuleringar per antal celler när måttet av intresse inte (direkt) är relaterat till densitet (t.ex. kinetisk energispektrum). Om man bortser från problem med parallell acceleration är simuleringen av konstantdensitetsflöden (t.ex. extern aerodynamik ) mer effektiv med rutnätsbaserade metoder än med SPH.

Exempel

Vätskedynamik

Fig. SPH-simulering av havsvågor med FLUIDS v.1 (Hoetzlein)

Hydrodynamik med utjämnade partiklar används i allt större utsträckning även för att modellera vätskerörelser . Detta beror på flera fördelar jämfört med traditionella rutnätsbaserade tekniker. För det första garanterar SPH bevarande av massa utan extra beräkning eftersom partiklarna själva representerar massa. För det andra beräknar SPH tryck från viktade bidrag från närliggande partiklar snarare än genom att lösa linjära ekvationssystem. Slutligen, till skillnad från rutnätsbaserade tekniker, som måste spåra vätskegränser, skapar SPH en fri yta för tvåfasinteragerande vätskor direkt eftersom partiklarna representerar den tätare vätskan (vanligtvis vatten) och det tomma utrymmet representerar den lättare vätskan (vanligtvis luft). Av dessa skäl är det möjligt att simulera vätskerörelser med hjälp av SPH i realtid. Men både rutnätsbaserade och SPH-tekniker kräver fortfarande generering av renderbar fri ytgeometri med användning av en polygoniseringsteknik som metakulor och marschkuber , punktstänkning eller visualisering av "matta". För gasdynamik är det mer lämpligt att använda själva kärnfunktionen för att producera en rendering av gaskolonndensitet (t.ex. som gjort i SPLASH-visualiseringspaketet).

En nackdel med rutnätsbaserade tekniker är behovet av ett stort antal partiklar för att producera simuleringar med likvärdig upplösning. I den typiska implementeringen av både enhetliga rutnät och SPH-partikeltekniker kommer många voxlar eller partiklar att användas för att fylla vattenvolymer som aldrig återges. Noggrannheten kan dock vara betydligt högre med sofistikerade rutnätsbaserade tekniker, särskilt de som är kopplade till partikelmetoder (som partikelnivåuppsättningar), eftersom det är lättare att upprätthålla inkompressibilitetsvillkoret i dessa system. SPH för vätskesimulering används alltmer i realtidsanimationer och spel där noggrannheten inte är lika kritisk som interaktivitet.

Det senaste arbetet i SPH för vätskesimulering har ökat prestanda, noggrannhet och användningsområden:

• B. Solenthaler, 2009, utvecklar Predictive-Corrective SPH (PCISPH) för att möjliggöra bättre inkompressibilitetsbegränsningar
• M. Ihmsen et al., 2010, introducerar gränshantering och adaptiv tidsstegring för PCISPH för noggranna stela kroppsinteraktioner
• K. Bodin et al., 2011, ersätter standardekvationen för tillståndstryck med en densitetsbegränsning och tillämpar en variationstidsintegrator
• R. Hoetzlein, 2012, utvecklar effektiv GPU-baserad SPH för stora scener i Fluids v.3
• N. Akinci et al., 2012, introducerar en mångsidig gränshantering och tvåvägs SPH-styv kopplingsteknik som är helt baserad på hydrodynamiska krafter; tillvägagångssättet är tillämpbart på olika typer av SPH-lösare
• M. Macklin et al., 2013 simulerar inkompressibla flöden inom ramen för Position Based Dynamics, för större tidssteg
• N. Akinci et al., 2013, introducerar en mångsidig ytspänning och tvåvägs vätske-fast vidhäftningsteknik som möjliggör simulering av en mängd intressanta fysiska effekter som observeras i verkligheten
• J. Kyle och E. Terrell, 2013, tillämpar SPH på helfilmssmörjning
• A. Mahdavi och N. Talebbeydokhti, 2015, föreslår en hybridalgoritm för implementering av fasta gränsvillkor och simulera flöde över en skarp krönad dam
• S. Tavakkol et al., 2016, utvecklar curvSPH, som gör den horisontella och vertikala storleken på partiklar oberoende och genererar enhetlig massfördelning längs krökta gränser
• W. Kostorz och A. Esmail-Yakas, 2020, föreslår en allmän, effektiv och enkel metod för att utvärdera normaliseringsfaktorer nära bitvis plana gränser
• Colagrossi et al., 2019, studerar flödet runt en cylinder nära en fri yta och jämför med andra tekniker

Astrofysik

Utjämnade partikelhydrodynamiks adaptiva upplösning, numeriska bevarande av fysiskt konserverade kvantiteter och förmåga att simulera fenomen som täcker många storleksordningar gör den idealisk för beräkningar inom teoretisk astrofysik .

Simuleringar av galaxbildning , stjärnbildning , stjärnkollisioner , supernovor och meteornedslag är några av den breda variationen av astrofysiska och kosmologiska användningar av denna metod.

SPH används för att modellera hydrodynamiska flöden, inklusive möjliga effekter av gravitation . Att införliva andra astrofysiska processer som kan vara viktiga, såsom strålningsöverföring och magnetfält är ett aktivt forskningsområde inom det astronomiska samfundet och har haft en viss begränsad framgång.

Solid mekanik

Libersky och Petschek utökade SPH till Solid Mechanics. Den största fördelen med SPH i denna applikation är möjligheten att hantera större lokal distorsion än nätbaserade metoder. Den här funktionen har utnyttjats i många tillämpningar inom solid Mechanics: metallformning, slag, spricktillväxt, brott, fragmentering, etc.

En annan viktig fördel med nätfria metoder i allmänhet, och med SPH i synnerhet, är att problem med nätberoende naturligtvis undviks med tanke på metodens nätfria karaktär. I synnerhet är mesh-inriktning relaterad till problem som involverar sprickor och det undviks i SPH på grund av det isotropiska stödet av kärnfunktionerna. Men klassiska SPH-formuleringar lider av draginstabilitet och brist på konsistens. Under de senaste åren har olika korrigeringar införts för att förbättra noggrannheten hos SPH-lösningen, vilket leder till RKPM av Liu et al. Randles och Libersky och Johnson och Beissel försökte lösa konsistensproblemet i sin studie av påverkansfenomen.

Dyka et al. och Randles och Libersky introducerade stresspunktintegreringen i SPH och Ted Belytschko et al. visade att stresspunktstekniken tar bort instabiliteten på grund av falska singulära lägen, medan draginstabiliteter kan undvikas genom att använda en lagrangisk kärna. Många andra nya studier finns i litteraturen som ägnas åt att förbättra konvergensen av SPH-metoden.

De senaste förbättringarna för att förstå konvergensen och stabiliteten hos SPH har möjliggjort mer utbredda tillämpningar inom solid Mechanics. Andra exempel på tillämpningar och utvecklingar av metoden är:

• Metallformningssimuleringar.
• SPH-baserad metod SPAM (Smoothed Particle Applied Mechanics) för slagbrott i fasta ämnen av William G. Hoover .
• Modifierad SPH (SPH/MLSPH) för fraktur och fragmentering.
• Taylor-SPH (TSPH) för stötvågsutbredning i fasta ämnen.
• Generalized coordinate SPH (GSPH) allokerar partiklar inhomogent i det kartesiska koordinatsystemet och arrangerar dem via kartläggning i ett generaliserat koordinatsystem där partiklarna är inriktade på ett enhetligt avstånd.

Numeriska verktyg

Interpolationer

Metoden Smoothed-Particle Hydrodynamics (SPH) fungerar genom att dela upp vätskan i en uppsättning diskreta rörliga element $i,j$ , kallade partiklar. Deras lagrangiska natur tillåter att ställa in deras position $\mathbf {r} _{i}$ genom integration av deras hastighet $\mathbf {v} _{i}$ som:

${\frac {\mathrm {d} {\boldsymbol {r}}_{i}}{\mathrm {d} t}}={\boldsymbol {v}}_{i}.$

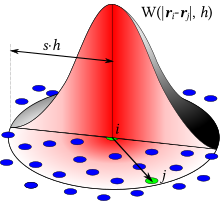
Dessa partiklar interagerar genom en kärnfunktion med karakteristisk radie känd som "utjämningslängden", typiskt representerad i ekvationer av $h$ . Detta innebär att den fysiska kvantiteten av vilken partikel som helst kan erhållas genom att summera de relevanta egenskaperna för alla partiklar som ligger inom kärnans intervall, varvid den senare används som en viktningsfunktion W {\displaystyle $}$ . Detta kan förstås i två steg. skrivs ett godtyckligt fält ${\displaystyle A} som en faltning med$$W$ :

$A({\boldsymbol {r}})=\int A\left({\boldsymbol {r^{\prime }}}\right)W(|{\boldsymbol {r}}-{\boldsymbol { r^{\prime }}}|,h)\,\mathrm {d} V\!\left({\boldsymbol {r'}}\right).$

Felet i att göra ovanstående approximation är ordning $h^{2}$ . För det andra approximeras integralen med hjälp av en Riemann-summering över partiklarna:

$A({\boldsymbol {r}})=\sum _{j}V_{j}A_{j }W(|{\boldsymbol {r}}-{\boldsymbol {r}}_{j}|,h),$

där summeringen över $j$ inkluderar alla partiklar i simuleringen. $V_{j}$ är volymen av partikel $j$ , $A_{j}$ är värdet på kvantiteten $A$ för partikel $j$ och ${\boldsymbol {r}}$ anger position. Till exempel kan densiteten $\rho _{i}$ för partikel $i$ uttryckas som:

$\rho _{i}=\rho ({\boldsymbol {r}}_{i})=\summa _{j}m_ {j}W_{ij},$

där $m_{j}=\rho _{j}V_{j}$ betecknar partikelmassan och $\rho _{j}$ partikeldensiteten, medan $W_{ij}=W_{ji}$ är en kort notation för $W(|{\boldsymbol {r}}_ {i}-{\boldsymbol {r}}_{j}|,h)$ . Felet vid approximering av integralen med en diskret summa beror på $h$ , på partikelstorleken (dvs ${\displaystyle V_{j}^{1/d}} ,$ d $\displaystyle d}$ är rymddimensionen), och på partikelarrangemanget i rymden. Den senare effekten är fortfarande dåligt känd.

Kärnfunktioner som vanligtvis används inkluderar Gauss-funktionen , den quintic spline och Wendland $C^{2}$ -kärnan. De två sistnämnda kärnorna stöds kompakt (till skillnad från Gauss, där det finns ett litet bidrag på valfritt ändligt avstånd), med stöd proportionellt mot $h$ . Detta har fördelen av att spara beräkningsansträngning genom att inte inkludera de relativt små bidragen från avlägsna partiklar.

Även om storleken på utjämningslängden kan fixeras i både rum och tid , utnyttjar detta inte den fulla kraften hos SPH. Genom att tilldela varje partikel sin egen utjämningslängd och låta den variera med tiden, kan upplösningen av en simulering fås att automatiskt anpassa sig efter lokala förhållanden. Till exempel, i ett mycket tätt område där många partiklar är nära varandra, kan utjämningslängden göras relativt kort, vilket ger hög rumslig upplösning. Omvänt, i lågdensitetsregioner där enskilda partiklar är långt ifrån varandra och upplösningen är låg, kan utjämningslängden ökas, vilket optimerar beräkningen för områdena av intresse.

Diskretisering av styrande ekvationer

För partiklar med konstant massa, differentiering av den interpolerade densiteten $\rho _{i}$ med avseende på tidsutbyten

${\frac {d\rho _{i}}{dt}}=\summa _{j}m_ {j}\left({\boldsymbol {v}}_{i}-{\boldsymbol {v}}_{j}\right)\cdot \nabla W_{ij},$

där $\nabla W_{ij}=-\nabla W_{ji}$ är gradienten för $W_{ij}$ med avseende på ${ \displaystyle {\boldsymbol {r}}_{i}}$ . Att jämföra denna ekvation med kontinuitetsekvationen i den lagrangiska beskrivningen (med materialderivator) ,

${\frac {d\rho }{dt}}=-\rho \nabla \cdot {\boldsymbol {v}},$

det är uppenbart att dess högra sida är en approximation av $-\rho \nabla \cdot \mathbf {v}$ ; därför definierar man en diskret divergensoperator enligt följande:

$\operatorname {D} _{i}\left\{{\boldsymbol {v}}_{j}\right\}=-{\frac {1}{\rho _{i}}}\summa _{j}m_{j}\left({\boldsymbol {v}}_{i}-{\boldsymbol {v}}_{j}\right)\cdot \nabla W_{ij}.$

Denna operator ger en SPH approximation av $\nabla \cdot \mathbf {v}$ vid partikeln $i$ för en given uppsättning partiklar med givna massor $m_{j}$ , positioner $\left\{\mathbf {r} _{j}\right\}$ och hastigheter $\left\{\mathbf {v} _{j} \right\}$ .

Den andra viktiga ekvationen för en komprimerbar inviscid vätska är Euler-ekvationen för momentumbalans:

${\frac {d{\boldsymbol {v}}}{dt}}=-{\frac {1}{\rho }}\nabla p+{\ fetstil {g}}$

På samma sätt som kontinuitet är uppgiften att definiera en diskret gradientoperator för att skriva

${\frac {d{\boldsymbol {v}}_{i}}{dt}}=-{\frac {1} {\rho }}\operatörsnamn {\mathbf {G} } _{i}\left\{p_{j}\right\}+{\boldsymbol {g}}$

Ett val är

$\operatorname {\mathbf {G} } _{i}\left \{p_{j}\right\}=\rho _{i}\sum _{j}m_{j}\left({\frac {p_{i}}{\rho _{i}^{2} }}+{\frac {p_{j}}{\rho _{j}^{2}}}\right)\nabla W_{ij},$

som har egenskapen att vara skew-adjoint med divergensoperatorn ovan, i den meningen att

$\sum _{i}V_{i}{\boldsymbol {v}} _{i}\cdot \operatörsnamn {\mathbf {G} } _{i}\left\{p_{j}\right\}=-\summa _{i}V_{i}p_{i}\operatörsnamn { D} _{i}\left\{{\boldsymbol {v}}_{j}\right\},$

detta är en diskret version av kontinuumidentiteten

$\int {\boldsymbol {v}}\cdot \operatörsnamn {grad} p=-\int p\operatörsnamn {div} \cdot {\boldsymbol {v}}.$

Denna fastighet leder till fina naturvårdsfastigheter.

Observera också att detta val leder till en symmetrisk divergensoperator och en antisymmetrisk gradient. Även om det finns flera sätt att diskretisera tryckgradienten i Euler-ekvationerna, är ovanstående antisymmetriska form den mest erkända. Det stöder strikt bevarande av linjärt och vinkelmomentum. Detta betyder att en kraft som utövas på partikel $i$ av partikel $j$ är lika med den som utövas på partikel $j$ av partikel $i$ inklusive teckenändringen av den effektiva riktningen, tack vare antisymmetriegenskapen $\nabla W_{ij}=-\nabla W_{ji}$ .

Ändå har andra operatörer föreslagits, som kan prestera bättre numeriskt eller fysiskt. Till exempel är en nackdel med dessa operatorer att medan divergensen $\operatorname {D}$ är nollordningens konsistent (dvs. ger noll när den appliceras på ett konstant vektorfält), kan det ses att gradienten ${ \displaystyle \operatorname {\mathbf {G} } }$ är det inte. Flera tekniker har föreslagits för att kringgå detta problem, vilket leder till åternormaliserade operatörer (se t.ex.).

Variationsprincip

Ovanstående SPH styrande ekvationer kan härledas från en minsta verkansprincip , med utgångspunkt från Lagrangian för ett partikelsystem:

${\mathcal {L}}=\sum _{j}m_{j}\left({\tfrac {1 }{2}}{\boldsymbol {v}}_{j}^{2}-e_{j}+{\boldsymbol {g}}\cdot {\boldsymbol {r}}_{j}\right)$ ,

där $e_{j}$ är den partikelspecifika inre energin . Euler -Lagrange-ekvationen för variationsmekanik lyder för varje partikel:

${\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial {\mathcal {L}}}{\partial {\boldsymbol {v}}_{i} }}={\frac {\partial {\mathcal {L}}}{\partial {\boldsymbol {r}}_{i}}}.$

När den appliceras på ovanstående Lagrangian ger den följande momentumekvation:

$m_{ i}{\frac {\mathrm {d} {\boldsymbol {v}}_{i}}{\mathrm {d} t}}=-\summa _{j}m_{j}{\frac {\partial e_{j}}{\partial {\boldsymbol {r}}_{i}}}+m_{i}{\boldsymbol {g}}=-\summa _{j}m_{j}{\frac {\ partiell e_{j}}{\partial \rho _{j}}}{\frac {\partial \rho _{j}}{\partial {\boldsymbol {r}}_{i}}}+m_{i }{\boldsymbol {g}}$

där kedjeregeln har använts, eftersom $e_{j}$ beror på ${\displaystyle \rho _{j}} ,$ och det senare, på partiklarnas position. Med den termodynamiska egenskapen $\mathrm {d} e=\left(p/\rho ^{2}\right)\mathrm {d} \rho$ kan vi skriva

$m_{i}{\frac {\mathrm {d} {\boldsymbol {v }}_{i}}{\mathrm {d} t}}=-\sum _{j}m_{j}{\frac {p_{j}}{\rho _{j}^{2}}} {\frac {\partial \rho _{j}}{\partial {\boldsymbol {r}}_{i}}}+m_{i}{\boldsymbol {g}},$

Att plugga in SPH-densitetsinterpolationen och differentiera explicit ${\displaystyle {\tfrac {\partial \rho _{j}}{\partial {\boldsymbol {r}}_{i}}}} leder$ till

${\frac {\mathrm {d} {\boldsymbol {v}} _{i}}{\mathrm {d} t}}=-\summa _{j}m_{j}\left({\frac {p_{i}}{\rho _{i}^{2}} }+{\frac {p_{j}}{\rho _{j}^{2}}}\right)\nabla W_{ij}+{\boldsymbol {g}},$

vilket är SPH-momentekvationen som redan nämnts, där vi känner igen operatorn ${\displaystyle \operatorname {\mathbf {G} } }.$ Detta förklarar varför linjärt rörelsemängd bevaras, och gör att bevarande av rörelsemängd och energi också kan bevaras.

Tidsintegration

Från det arbete som gjordes på 80- och 90-talen med numerisk integrering av punktliknande partiklar i stora acceleratorer, har lämpliga tidsintegratorer utvecklats med noggranna bevarandeegenskaper på lång sikt; de kallas symplektiska integratörer . Det mest populära i SPH-litteraturen är leapfrog -schemat, som läser för varje partikel $i$ :

${\begin{aligned}{\boldsymbol {v}}_{i}^{n+1/2}&={\boldsymbol {v}}_ {i}^{n}+{\boldsymbol {a}}_{i}^{n}{\frac {\Delta t}{2}},\\{\boldsymbol {r}}_{i}^ {n+1}&={\boldsymbol {r}}_{i}^{n}+{\boldsymbol {v}}_{i}^{i+1/2}\Delta t,\\{\ fetsymbol {v}}_{i}^{n+1}&={\boldsymbol {v}}_{i}^{n+1/2}+{\boldsymbol {a}}_{i}^{ i+1}{\frac {\Delta t}{2}},\end{aligned}}$

där $\Delta t$ är tidssteget, upphöjd står för tidsiterationer medan ${\boldsymbol {a}}_{i}$ är partikelaccelerationen, given av höger sida av momentumekvationen.

Andra symplektiska integratörer finns (se referensläroboken). Det rekommenderas att använda ett symplektiskt schema (även av låg ordning) istället för ett icke-symplektiskt schema av hög ordning, för att undvika felackumulering efter många iterationer.

Integrering av densitet har inte studerats utförligt (se nedan för mer information).

Symplektiska scheman är konservativa men explicita, så deras numeriska stabilitet kräver stabilitetsförhållanden, analogt med Courant-Friedrichs-Lewy-tillståndet (se nedan ).

Gränstekniker

SPH Convolution-stöd delas nära en gräns

Om SPH-falsningen ska praktiseras nära en gräns, dvs närmare än s · h , så trunkeras det integrerade stödet. Faktum är att när faltningen påverkas av en gräns, ska faltningen delas i 2 integraler,

$A({\boldsymbol {r}})=\int _{\Omega ({\boldsymbol {r}})}A\left({\boldsymbol {r^ {\prime }}}\right)W(|{\boldsymbol {r}}-{\boldsymbol {r^{\prime }}}|,h)d{\boldsymbol {r^{\prime }}}+ \int _{B({\boldsymbol {r}})-\Omega ({\boldsymbol {r}})}A\left({\boldsymbol {r^{\prime }}}\right)W(|{ \boldsymbol {r}}-{\boldsymbol {r^{\prime }}}|,h)d{\boldsymbol {r^{\prime }}},$

där B( r ) är den kompakta stödkulan centrerad vid r , med radien s · h , och Ω( r ) anger delen av det kompakta stödet inuti beräkningsdomänen, Ω ∩ B( r ) . Att införa gränsvillkor i SPH är därför helt baserat på att approximera den andra integralen på höger sida. Detsamma kan naturligtvis tillämpas på differentialoperatorernas beräkning,

$\nabla A({\boldsymbol {r}})=\int _{\Omega ({\boldsymbol {r}})}A\left({\boldsymbol {r^{\prime }}}\right )\nabla W({\boldsymbol {r}}-{\boldsymbol {r^{\prime }}},h)d{\boldsymbol {r^{\prime }}}+\int _{B({\ fetsymbol {r}})-\Omega ({\boldsymbol {r}})}A\left({\boldsymbol {r^{\prime }}}\right)\nabla W({\boldsymbol {r}}- {\boldsymbol {r^{\prime }}},h)d{\boldsymbol {r^{\prime }}}.$

Flera tekniker har introducerats tidigare för att modellera gränser i SPH.

Integral försummelse

SPH fri yta modell med hjälp av integrerad försummelse

Den enklaste gränsmodellen är att försumma integralen,

$\int _{B({\boldsymbol {r}})-\Omega ({\boldsymbol {r}})}A\left({\boldsymbol {r^{\prime }}}\right)\nabla W({\boldsymbol {r}}-{\boldsymbol {r^{\prime }}},h)d{\boldsymbol {r^{\prime }}}\simeq {\boldsymbol {0}},$

så att bara bulkinteraktionerna tas med i beräkningen,

$\nabla A_{i}=\sum _{j\in \Omega _{i}}V_{j}A_{j}\nabla W_{ij}.$

Detta är ett populärt tillvägagångssätt när fri yta beaktas i monofassimuleringar.

Den största fördelen med detta gränsvillkor är dess uppenbara enkelhet. Flera konsekvensfrågor ska dock beaktas när denna gränsteknik tillämpas. Det är faktiskt en tung begränsning av dess potentiella tillämpningar.

Fluid Extension

SPH Fluid Extension Boundary-teknik

Förmodligen den mest populära metoden, eller åtminstone den mest traditionella, för att införa gränsvillkor i SPH, är Fluid Extension-teknik. En sådan teknik bygger på att fylla det kompakta stödet över gränsen med så kallade spökpartiklar, vilket bekvämt sätter deras fältvärden.

Längs denna linje kan metoden för integral neglekt betraktas som ett särskilt fall av vätskeförlängningar, där fältet A försvinner utanför beräkningsdomänen.

Den största fördelen med denna metod är enkelheten, förutsatt att gränsbidraget beräknas som en del av bulkinteraktionerna. Denna metod har också analyserats djupt i litteraturen.

Å andra sidan är det inte en trivial uppgift att distribuera spökpartiklar i den trunkerade domänen, så att modellering av komplexa gränsformer blir besvärlig. De två mest populära metoderna för att fylla den tomma domänen med spökpartiklar är Mirrored-Particles och Fixed-Particles.

Gränsintegral

SPH Boundary Integral modell

Den senaste Boundary-tekniken är Boundary Integral-metoden. I denna metodik ersätts den tomma volymintegralen med en ytintegral och en renormalisering:

$nabla A_{i}={ \frac {1}{\gamma _{i}}}\left(\sum _{j\in \Omega _{i}}V_{j}A_{j}\nabla W_{ij}+\summa _{ j\in \partial \Omega _{i}}S_{j}A_{j}{\boldsymbol {n}}_{j}W_{ij}\right),}$

$\gamma _{i}=\sum _{j\in \Omega _{i}}V_{j}W_{ij},$

med n _j normalen för det generiska j :te gränselementet. Yttermen kan också lösas med tanke på ett semi-analytiskt uttryck.

Modellerande fysik

Hydrodynamik

Svagt komprimerbart tillvägagångssätt

Ett annat sätt att bestämma densiteten är baserat på själva SPH-utjämningsoperatören. Därför uppskattas densiteten från partikelfördelningen med användning av SPH- interpolation . För att övervinna oönskade fel på den fria ytan genom kärntrunkering, kan densitetsformuleringen återigen integreras i tid.

Den svagt komprimerbara SPH i vätskedynamik är baserad på diskretiseringen av Navier–Stokes-ekvationerna eller Euler-ekvationerna för komprimerbara vätskor. För att stänga systemet används en lämplig tillståndsekvation för att länka tryck $p$ och densitet $\rho$ . I allmänhet används den så kallade Cole-ekvationen (ibland felaktigt kallad " Tait-ekvationen ") i SPH. Det står

$p={\frac {\rho _{0}c^{2}}{\gamma }}\left(\left( {\frac {\rho }{\rho _{0}}}\right)^{\gamma }-1\right)+p_{0},$

där $\rho _{0}$ är referensdensiteten och $c$ ljudhastigheten . För vatten används vanligtvis ${\displaystyle \gamma =7} .$ Bakgrundstrycket $p_{0}$ läggs till för att undvika negativa tryckvärden.

Verkliga nästan inkompressibla vätskor som vatten kännetecknas av mycket hög ljudhastighet av storleksordningen $10^{3}\mathrm {m/s}$ . Därför färdas tryckinformation snabbt jämfört med det faktiska bulkflödet, vilket leder till mycket små Mach-tal $M$ . Momentumekvationen leder till följande samband:

${\frac {\delta \rho }{\rho _{0}}}\approx {\frac {|{\boldsymbol {v}}|}{c^{2}}} =M^{2}$

där $\rho$ är densitetsändringen och $v$ hastighetsvektorn. I praktiken antas ett värde på c mindre än det verkliga för att undvika tidssteg som är för små i tidsintegrationsschemat. I allmänhet används en numerisk ljudhastighet så att densitetsvariationer mindre än 1 % tillåts. Detta är det så kallade antagandet om svag kompressibilitet. Detta motsvarar ett Mach-tal mindre än 0,1, vilket innebär:

$c=10v_{\text{max}}$

där den maximala hastigheten $v_{\text{max}}$ behöver uppskattas, till exempel genom Torricellis lag eller en välgrundad gissning. Eftersom endast små densitetsvariationer förekommer, kan en linjär tillståndsekvation antas:

$p=c^{2}\left(\rho -\rho _{0}\right)$

Vanligtvis påverkas de svagt komprimerbara systemen av ett högfrekvent falskt brus på tryck- och densitetsfälten. Detta fenomen orsakas av den olinjära interaktionen mellan akustiska vågor och av att schemat är explicit i tid och centrerat i rymden.

Genom åren har flera tekniker föreslagits för att bli av med detta problem. De kan delas in i tre olika grupper:

1. scheman som använder densitetsfilter,
2. modellerna som lägger till en diffusiv term i kontinuitetsekvationen,
3. scheman som använder Riemann-lösare för att modellera partikelinteraktionen.

Densitetsfilterteknik

Scheman för den första gruppen applicerar ett filter direkt på densitetsfältet för att ta bort det falska numeriska bruset. De mest använda filtren är MLS (moving least squares) och Shepard-filtret som kan appliceras vid varje tidssteg eller vart n:e tidssteg. Ju vanligare användningen av filtreringsproceduren är, desto mer regelbundna densitets- och tryckfält erhålls. Å andra sidan leder detta till en ökning av beräkningskostnaderna. I långtidssimuleringar kan användningen av filtreringsproceduren leda till störningar av den hydrostatiska tryckkomponenten och till en inkonsekvens mellan den globala vätskevolymen och densitetsfältet. Vidare säkerställer det inte upprätthållandet av det dynamiska gränsvillkoret för fri yta.

Diffusiv term teknik

Ett annat sätt att jämna ut densitets- och tryckfältet är att lägga till en diffusiv term i kontinuitetsekvationen (grupp 2):

${\displaystyle {\frac {d\rho _{i}}{dt} }=\summa _{j}m_{j}\left({\boldsymbol {v}}_{i}-{\boldsymbol {v}}_{j}\right)\cdot \nabla W_{ij}+ {\mathcal {D}}_{i}(\rho ),}$

De första scheman som antog ett sådant tillvägagångssätt beskrevs i Ferrari och i Molteni där den diffusiva termen modellerades som en Laplacian av täthetsfältet. Ett liknande tillvägagångssätt användes också i Fatehi och Manzari.

SPH-simulering: tryckfördelning av ett dambrottsflöde med standard SPH-formulering

SPH-simulering: tryckfördelning av ett dambrottsflöde med standard δ-SPH-formulering

I Antuono et al. en korrigering av den diffusiva termen för Molteni föreslogs för att ta bort några inkonsekvenser nära den fria ytan. I detta fall är den antagna diffusiva termen ekvivalent med en differentialoperator av hög ordning på densitetsfältet. Schemat kallas δ-SPH och bevarar alla bevarandeegenskaper hos SPH utan diffusion (t.ex. linjära och vinkelmoment, total energi, se ) tillsammans med en jämn och regelbunden representation av densitets- och tryckfälten.

I den tredje gruppen finns de SPH-scheman som använder numeriska flöden erhållna genom Riemann-lösare för att modellera partikelinteraktionerna.

Riemann lösningsteknik

SPH-simulering: tryckfördelning av ett dambrottsflöde med Riemann-lösare med lågförlustbegränsare.

För en SPH-metod baserad på Riemann-lösare konstrueras ett interpartikel-Riemannproblem längs en enhetsvektor $\mathbf {e} _{ij}=-\mathbf { r} _{ij}/r_{ij}$ pekar form partikel $i$ till partikel $j$ . I detta Riemann-problem är de initiala vänstra och högra tillstånden på partiklar $i$ respektive $j$ . Tillstånden $L$ och $R$ är

$${\begin{cases}(\rho _{L},U_{L},P_{L})=(\rho _{i},\mathbf {v} _{i}\cdot \mathbf { e} _{ij},P_{i})\\(\rho _{R},U_{R},P_{R})=(\rho _{j},\mathbf {v} _{j} \cdot \mathbf {e} _{ij},P_{j}).\end{cases}}$$

Lösningen av Riemann-problemet resulterar i tre vågor som utgår från diskontinuiteten. Två vågor, som kan vara stöt- eller sällsyntningsvågor, färdas med den minsta eller största våghastigheten. Mellanvågen är alltid en kontaktdiskontinuitet och separerar två mellanliggande tillstånd, betecknade med $^{\ast },U_{L}^ {\ast },P_{L}^{\ast })}$ och $(\rho _{R}^{\ast },U_{R} ^{\ast },P_{R}^{\ast })$ . Genom att anta att det mellanliggande tillståndet uppfyller $U_{L}^{\ast }=U_{R}^{\ast }=U^{\ast }$ och ${\displaystyle P_{L}^{\ast }=P_{R}^{\ast }=P^{\ast }} , en linjär Riemann-lösare för jämna flöden eller med endast$ måttliga starka stötar kan skrivas som

$$\displaystyle {\begin{cases}U^$$

där ${\displaystyle {\overline {U}}=(U_{L}+U_{R})/2$${\overline {P}}=(P_{L}+P_{R})/2$ och är medelvärden mellan partiklar. Med lösningen av Riemann-problemet, dvs $U^{\ast }$ och $P^{\ast }$ , är diskretiseringen av SPH-metoden

$${\frac {d\rho _{i}}{dt}}=2 \rho _{i}\summa _{j}{\frac {m_{j}}{\rho _{j}}}(\mathbf {v} _{i}-\mathbf {v} ^{\ast })\cdot \nabla _{i}W_{ij},$$

$${\frac {d\mathbf {v} _{i}}{dt}}=-2\sum _{j}m_{j}\left({\frac {P^{\ast }}{ \rho _{i}\rho _{j}}}\right)\nabla _{i}W_{ij}.$$

där $\mathbf {v} ^{\ast }=U^{\ast }\mathbf {e} _{ij }+({\overline {\mathbf {v} }}_{ij}-{\overline {U}}\mathbf {e} _{ij})$ . Detta indikerar att medelhastigheten och trycket mellan partiklarna helt enkelt ersätts av lösningen av Riemann-problemet. Genom att jämföra båda kan man se att den mellanliggande hastigheten och trycket från medelvärdena mellan partiklarna uppgår till implicit dissipation, dvs densitetsregularisering respektive numerisk viskositet.

Eftersom ovanstående diskretisering är mycket dissipativ är en enkel modifiering att tillämpa en limiter för att minska de implicita numeriska dissipationerna som introduceras genom att begränsa det mellanliggande trycket med

$$P^{\ast }={\overline {P}}+{\frac {1}{2}}\beta { \overline {\rho }}{(U_{L}-U_{R})},$$

där begränsaren definieras som

$$\beta =\min {\big (}\eta \max(U_{L}-U_{R},0),{\overline {c}}{\big )}.$$

Observera att $\beta$ säkerställer att det inte sker någon avledning när vätskan påverkas av en expansionsvåg, dvs ${\displaystyle U_{L}<U_{R}},$ och att parameter $\eta$ , används för att modulera förlust när vätskan påverkas av en kompressionsvåg, dvs $U_{L}\geq U_{R}$ . Numeriska experiment fann att $\eta =3$ är generellt effektiv. Observera också att förlusten som introduceras av den mellanliggande hastigheten inte är begränsad.

Viskositetsmodellering

I allmänhet kräver beskrivningen av hydrodynamiska flöden en bekväm behandling av diffusiva processer för att modellera viskositeten i Navier –Stokes ekvationer . Det behöver särskilt beaktas eftersom det involverar Laplacian differentialoperatör. Eftersom den direkta beräkningen inte ger tillfredsställande resultat har flera metoder för att modellera diffusionen föreslagits.

• Artificiell viskositet

Introducerad av Monaghan och Gingold användes den artificiella viskositeten för att hantera vätskeflöden med högt Mach-tal . Det står

$\Pi _{ij}= {\begin{cases}{\dfrac {-\alpha {\bar {c}}_{ij}\phi _{ij}+\beta \phi _{ij}^{2}}{{\bar {\ rho }}_{ij}}}&\quad {\boldsymbol {v}}_{ij}\cdot {\boldsymbol {r}}_{ij}<0\\0&\quad {\boldsymbol {v}} _{ij}\cdot {\boldsymbol {r}}_{ij}\geq 0\end{cases}}$

Här styr $\alpha$ en volymviskositet medan $\beta$ fungerar på samma sätt som Neumann Richtmeyrs artificiella viskositet. ϕ $\phi _{ij}$ av

$\phi _{ij}={\frac {h{\boldsymbol {v}}_{ij}\cdot {\boldsymbol {r}}_{ij}}{\Vert {\boldsymbol {r}} _{ij}\Vert ^{2}+\eta _{h}^{2}}}.$

Den artificiella viskositeten har också visat sig förbättra den totala stabiliteten för generella flödessimuleringar. Därför tillämpas den på inviscid problem i följande form

$\Pi _{ij}=\alpha hc{\frac {{\boldsymbol {v}}_{ij}\cdot {\boldsymbol {r}}_{ij}}{\Vert {\boldsymbol {r }}_{ij}\Vert ^{2}+\eta _{h}^{2}}}.$

Det är möjligt att inte bara stabilisera inviscid simuleringar utan också att modellera den fysiska viskositeten genom detta tillvägagångssätt. Att göra så

$\alpha hc=2(n+2){\frac {\mu }{\rho }}$

ersätts i ekvationen ovan, där $n$ är antalet spartiella dimensioner av modellen. Detta tillvägagångssätt introducerar bulkviskositeten $\zeta ={\frac {5}{3}}\mu$ .

• Morris

För låga Reynolds-tal föreslogs viskositetsmodellen av Morris.

$[\nu \Delta {\boldsymbol {v}}]_{ij}={\frac {2\nu }{\rho _{j}}}\,{\frac {{\boldsymbol {r} }_{ij}\cdot \nabla w_{h,ij}}{\Vert {\boldsymbol {r}}_{ij}\Vert ^{2}+\eta _{h}^{2}}}\ ,{\boldsymbol {v}}_{ij}.$

• LoShao

Ytterligare fysik

• Ytspänning
• Värmeöverföring
• Turbulens

Astrofysik

Ofta inom astrofysik vill man modellera självgravitation utöver ren hydrodynamik. Den partikelbaserade naturen hos SPH gör den idealisk att kombinera med en partikelbaserad gravitationslösare, till exempel trädgravitationskod , partikelnät eller partikel-partikelpartikelnät .

Solid mekanik och vätskestrukturinteraktion (FSI)

Total lagrangisk formulering för fast mekanik

, introduceras först en korrigeringsmatris ${\displaystyle \mathbb {B} ^{0}} för att återskapa rotation av stel kropp som$

$\mathbb {B} _{a}^{0}=\left(\summa _{b} V_{b}^{0}\left(\mathbf {r} _{b}^{0}-\mathbf {r} _{a}^{0}\right)\otimes \nabla _{a}^ {0}W_{ab}\right)^{-1}$

 

 

 

 

()

var

$$\nabla _{a}^{0}W_{a}={\frac {\partial W\left(|\mathbf {r} _{ab}^{0}|,h\right )}{\partial |\mathbf {r} _{ab}^{0}|}}\mathbf {e} _{ab}^{0}$$

står för gradienten för kärnfunktionen utvärderad vid den initiala referenskonfigurationen. Observera att nedsänkta $a$ och $b$ används för att beteckna fasta partiklar, och utjämningslängden $h$ är identisk med den i diskretiseringen av vätskeekvationer.

Med den initiala konfigurationen som referens utvärderas den fasta densiteten direkt som

$\rho _{a}=\rho _{a}^{0}{\frac {1}{J}}$

 

 

 

 

()

där $J=\det(\mathbb {F} )$ är den jakobianska determinanten för deformationstensor $\mathbb {F}$ .

Vi kan nu diskretisera momentumekvationen i följande form

$m_{a}{\frac {{\ text{d}}\mathbf {v} }{{\text{d}}t}}=2\summa _{b}V_{a}V_{b}{\tilde {\mathbb {P} }}_ {ab}\nabla _{a}^{0}W_{ab}+\mathbf {g} +\mathbf {f} _{a}^{F:p}+\mathbf {f} _{a}^ {F:v}$

 

 

 

 

()

där interpartikelmedelvärde först Piola-Kirchhoff spänning ${\tilde {\mathbb {P} }}$ definieras som

${\tilde {\mathbb {P} }}_{ab}={\frac {1}{2}}\left(\mathbb {P} _{a}\mathbb {B} _{a} ^{0}+\mathbb {P} _{b}\mathbb {B} _{b}^{0}\right).$

 

 

 

 

()

Även $\mathbf {f} _{a}^{F:p}$ och $\mathbf {f} _{a}^{F:v}$ motsvarar vätsketrycket och viskösa krafter som verkar på den fasta partikeln $a$ .

Vätskestrukturkoppling

Vid vätskestrukturkoppling uppträder den omgivande fasta strukturen som en rörlig gräns för vätska, och det halkfria gränsvillkoret åläggs vid vätske-strukturgränsytan. Interaktionen tvingar $\mathbf {f} _{i}^{S:p}$ och $\mathbf {f} _{i}^{S:v }$ som verkar på en flytande partikel $i$ , på grund av närvaron av den intilliggande fasta partikeln $a$ , kan erhållas som

$\mathbf {f} _ {i}^{S:p}=-2\summa _{a}V_{i}V_{a}{\frac {p_{i}\rho _{a}^{d}+p_{a}^ {d}\rho _{i}}{\rho _{i}+\rho _{a}^{d}}}\nabla _{i}W(\mathbf {r} _{ia},h)$

 

 

 

 

()

och

$\mathbf {f} _{i}^{S:v}=2\summa _{a}\eta V_{i}V_{a}{\frac {\mathbf {v} _{i}- \mathbf {v} _{a}^{d}}{r_{ia}}}{\frac {\partial W(\mathbf {r} _{ia},h)}{\partial {{r}_ {ia}}}}.$

 

 

 

 

()

definieras det imaginära trycket $p_{a}^{d}$ och hastigheten ${\displaystyle \mathbf {v} _{a}^{d}} av$

${\begin{cases}p_{a}^{d}=p_{i}+\rho _{i}\max(0,(\mathbf {g} -{\frac {{\text{d }}\mathbf {v} _{a}}{{\text{d}}t}})\cdot \mathbf {n} ^{S})(\mathbf {r} _{ia}\cdot \mathbf {n} ^{S})\\\mathbf {v} _{a}^{d}=2\mathbf {v} _{i}-\mathbf {v} _{a}.\end{cases} }$

 

 

 

 

()

där $\mathbf {n} ^{S}$ anger ytnormalriktningen för den fasta strukturen, och den imaginära partikeldensiteten $\rho _{a}^{d}$ beräknas genom tillståndsekvationen.

Följaktligen tvingar interaktionen $\mathbf {f} _{a}^{F:p}$ och $\mathbf {f} _{a}^{F :v}$ som verkar på en fast partikel $a$ ges av

$\mathbf {f} _ {a}^{F:p}=-2\summa _{i}V_{a}V_{i}{\frac {p_{a}^{d}\rho _{i}+p_{i}\ rho _{a}^{d}}{\rho _{i}+\rho _{a}^{d}}}\nabla _{a}W(\mathbf {r} _{ai},h)$

 

 

 

 

()

och

$\mathbf {f} _{a}^{F:v}=2\summa _{i}\eta V_{a}V_{i}{\frac {\mathbf {v} _{a}^ {d}-\mathbf {v} _{i}}{r_{ia}}}{\frac {\partial W(\mathbf {r} _{ia},h)}{\partial {{r}_ {ai}}}}.$

 

 

 

 

()

Den antisymmetriska egenskapen hos derivatan av kärnfunktionen säkerställer momentumbevarandet för varje par av interagerande partiklar $i$ och $a$ .

Andra

för diskreta element , som används för att simulera granulära material , är relaterad till SPH.

Vidare läsning

• Hoover, WG (2006). Smooth Particle Applied Mechanics: The State of the Art, World Scientific.
• Impact Modeling med SPH Stellingwerf, RF, Wingate, CA, Memorie della Societa Astronomia Italiana, Vol. 65, sid. 1117 (1994).
• Amada, T., Imura, M., Yasumuro, Y., Manabe, Y. och Chihara, K. (2004) Partikelbaserad vätskesimulering på GPU, i ACM Workshop on General-purpose Computing on Graphics Processors (augusti) , 2004, Los Angeles, Kalifornien).
• Desbrun, M. och Cani, MP. (1996). Smoothed Particles: ett nytt paradigm för att animera mycket deformerbara kroppar. In Proceedings of Eurographics Workshop on Computer Animation and Simulation (augusti 1996, Poitiers, Frankrike).
• Hegeman, K., Carr, NA och Miller, GSP Partikelbaserad vätskesimulering på GPU. In Proceedings of International Conference on Computational Science (Reading, Storbritannien, maj 2006). Proceedings publicerad som Lecture Notes in Computer Science v. 3994/2006 (Springer-Verlag).
• M. Kelager. (2006) Lagrangian Fluid Dynamics Using Smoothed Particle Hydrodynamics, M. Kelagar (MS Thesis, Univ. Copenhagen).
• Kolb, A. och Cuntz, N. (2005). Dynamisk partikelkoppling för GPU-baserad vätskesimulering. I Proceedings of the 18th Symposium on Simulation Techniques (2005) s. 722–727.
• Liu, GR och Liu, MB Smoothed Particle Hydrodynamics: en meshfri partikelmetod. Singapore: World Scientific (2003).
• Monaghan, JJ (1992). Utjämnad partikelhydrodynamik. Annu. Rev Astron. Astrofys. (1992). 30: 543–74.
• Muller, M., Charypar, D. och Gross, M. Partikelbaserad vätskesimulering för interaktiva applikationer, In Proceedings of Eurographics/SIGGRAPH Symposium on Computer Animation (2003), eds. D. Breen och M. Lin.
• Vesterlund, M. Simulering och rendering av en viskös vätska med utjämnad partikelhydrodynamik, (MS Thesis, Umeå universitet, Sverige).
• Violeau, D., Fluid Mechanics och SPH-metoden. Oxford University Press (2012).

externa länkar

• Första stora simuleringen av stjärnbildning med SPH
• SPHERIC (SPH research and engineering International Community)
• ITVO är webbplatsen för The Italian Theoretical Virtual Observatory skapad för att söka efter en databas med numeriska simuleringsarkiv.
• SPHC Bildgalleri visar en mängd olika testfall, experimentella valideringar och kommersiella tillämpningar av SPH-koden SPHC.
• En härledning av SPH-modellen utgående från Navier-Stokes ekvationer

programvara

• Algodoo är ett 2D-simuleringsramverk för utbildning med SPH
• AQUAgpusph är forskarnas fria (GPLv3) SPH, av forskarna, för forskarna
• dive solutions är en kommersiell webbaserad SPH-teknikmjukvara för CFD-ändamål
• DualSPHysics är en mestadels öppen källkod SPH-kod baserad på SPHysics och använder GPU-beräkning. Komponenterna med öppen källkod är tillgängliga under LGPL.
• FLUIDS v.1 är en enkel, öppen källkod (Zlib), realtids 3D SPH-implementering i C++ för vätskor för CPU och GPU.
• Fluidix är ett GPU-baserat partikelsimulerings-API tillgängligt från OneZero Software
• GADGET [1] är en fritt tillgänglig ( GPL ) kod för kosmologiska N-kroppar/SPH-simuleringar
• GPUSPH SPH-simulator med viskositet (GPLv3)
• Pasimodo är ett programpaket för partikelbaserade simuleringsmetoder, t.ex. SPH
• LAMMPS är en massivt parallell, öppen källkod för klassisk molekylär dynamik som kan utföra SPH-simuleringar
• Physics Abstraction Layer är ett abstraktionssystem med öppen källkod som stöder realtidsfysikmotorer med SPH-stöd
• PreonLab är en kommersiell ingenjörsprogramvara utvecklad av FIFTY2 Technology som implementerar en implicit SPH-metod
• Punto är ett fritt tillgängligt visualiseringsverktyg för partikelsimuleringar
• pysph Open Source Framework för Smoothed Particle Hydrodynamics i Python (ny BSD-licens)
• Py-SPHViewer Open Source pythonvisualiseringsverktyg för utjämnade partikelhydrodynamiksimuleringar.
• RealFlow Commercial SPH-lösare för biografbranschen.
• RheoCube är en kommersiell SaaS- produkt från Electric Ant Lab som kopplar mesoskopiska SPH-modeller med mikroskaliga MD- simuleringar.
• SimPARTIX är ett kommersiellt simuleringspaket för SPH och Discrete Element Method (DEM) simuleringar från Fraunhofer IWM
• SPH-flöde
• SPHERA
• SPHinXsys är ett SPH-bibliotek med öppen källkod med flera fysik och flera upplösningar. Den tillhandahåller C++ API:er för fysisk exakt simulering och syftar till att modellera kopplade industriella dynamiska system inklusive flytande, solid, multi-body dynamik och mer.
• SPHysics är en SPH-implementering med öppen källkod i Fortran
• SPLASH är ett visualiseringsverktyg med öppen källkod (GPL) för SPH-simuleringar
• SYMPLER : En SYMbolisk partikelsimulator med gratisprogram från University of Freiburg.
• Nauticle är ett allmänt beräkningsverktyg för partikelbaserade numeriska metoder.
• NDYNAMICS är en kommersiell vätskesimuleringsmjukvara baserad på implicit SPH utvecklad av CENTROID LAB som för närvarande används för interna/externa översvämnings-/kärnkrafts-/kemitekniska applikationer.