Mesh generation

Finita elementnät av fyrhörningar i en krökt domän.

Mesh-generering är metoden att skapa ett nät , en uppdelning av ett kontinuerligt geometriskt utrymme i diskreta geometriska och topologiska celler. Ofta bildar dessa celler ett enkelt komplex . Vanligtvis partitionerar cellerna den geometriska ingångsdomänen. Mesh-celler används som diskreta lokala approximationer av den större domänen. Mesh skapas av datoralgoritmer, ofta med mänsklig vägledning genom ett GUI , beroende på domänens komplexitet och vilken typ av mesh som önskas. Ett typiskt mål är att skapa ett nät som exakt fångar indatadomänens geometri, med högkvalitativa (välformade) celler och utan så många celler att efterföljande beräkningar blir svårlösta. Nätet ska också vara fint (ha små element) i områden som är viktiga för de efterföljande beräkningarna.

Nätor används för rendering till en datorskärm och för fysisk simulering som finita elementanalys eller beräkningsvätskedynamik . Nätverk är sammansatta av enkla celler som trianglar eftersom vi till exempel vet hur man utför operationer som finita elementberäkningar (teknik) eller strålspårning (datorgrafik) på trianglar, men vi vet inte hur man utför dessa operationer direkt på komplicerade utrymmen och former som en vägbro. Vi kan simulera styrkan på bron, eller rita den på en datorskärm, genom att utföra beräkningar på varje triangel och beräkna växelverkan mellan trianglar.

En stor skillnad är mellan strukturerad och ostrukturerad meshing. I strukturerad meshning är nätet ett vanligt gitter, såsom en array, med underförstådd anslutning mellan element. I ostrukturerad meshing kan element vara kopplade till varandra i oregelbundna mönster, och mer komplicerade domäner kan fångas. Den här sidan handlar i första hand om ostrukturerade maskor. Även om ett nät kan vara en triangulering , skiljer sig processen för mesh från punktuppsättningstriangulering genom att mesh inkluderar friheten att lägga till hörn som inte finns i inmatningen. "Facetering" (triangulering) CAD -modeller för ritning har samma frihet att lägga till hörn, men målet är att representera formen korrekt med så få trianglar som möjligt och formen på individuella trianglar är inte viktig. Datorgrafiska renderingar av texturer och realistiska ljusförhållanden använder mesh istället.

Många mesh-genereringsprogram är kopplade till ett CAD-system som definierar dess inmatning, och simuleringsprogramvara för att ta dess utdata. Ingången kan variera mycket men vanliga former är Solid modellering , Geometric modellering , NURBS , B-rep , STL eller ett punktmoln .

Terminologi

Termerna " nätgenerering " " nätgenerering " " mesh " " och " nät " används ofta omväxlande, även om de två sistnämnda strängt taget är bredare och omfattar nätförbättring: att ändra nätet med målet att öka hastigheten eller noggrannheten hos de numeriska beräkningarna som kommer att utföras över den. I datorgrafikåtergivning och matematik kallas ett nät ibland för en tessellation .

Nätansikter (celler, entiteter) har olika namn beroende på deras dimension och det sammanhang i vilket nätet kommer att användas. I finita element kallas de högstdimensionella mesh-enheterna "element", "kanter" är 1D och "noder" är 0D. Om elementen är 3D är 2D-entiteterna "ansikten". I beräkningsgeometri kallas 0D-punkterna för hörn. Tetraedrar förkortas ofta som "tets"; trianglar är "tris", fyrhörningar är "quads" och hexaedrar (topologiska kuber) är "hexes".

Tekniker

Catmull-Clark indelning av en yta

Triangulering av en implicit yta

Många meshing-tekniker bygger på principerna för Delaunay-trianguleringen , tillsammans med regler för att lägga till hörn, såsom Rupperts algoritm . En utmärkande egenskap är att ett initialt grovt nät av hela utrymmet bildas, sedan läggs hörn och trianglar till. Däremot startar framskridande frontalgoritmer från domängränsen och lägger till element som stegvis fyller upp interiören. Hybridtekniker gör båda. En speciell klass av avancerade fronttekniker skapar tunna gränsskikt av element för vätskeflöde. Vid generering av strukturerade nät är hela nätet ett gitterdiagram , till exempel ett vanligt rutnät av kvadrater. I blockstrukturerad mesh är domänen uppdelad i stora subregioner, som var och en är ett strukturerat mesh. Vissa direkta metoder börjar med ett blockstrukturerat nät och flyttar sedan nätet för att anpassa sig till inmatningen; se Automatisk Hex-Mesh Generation baserad på polycube . En annan direkt metod är att skära de strukturerade cellerna genom domängränsen; se skulptera baserad på Marching cubes .

Vissa typer av maskor är mycket svårare att skapa än andra. Enkla maskor tenderar att vara lättare än kubiska maskor. En viktig kategori är att generera ett sexkantnät som överensstämmer med ett fast nät med fyrkantig yta; ett forskningsdelområde studerar förekomsten och genereringen av maskor av specifika små konfigurationer, såsom den tetragonala trapetsen . På grund av svårigheten med detta problem har förekomsten av kombinatoriska hex-maskor studerats förutom problemet med att generera goda geometriska realiseringar. Medan kända algoritmer genererar enkla maskor med garanterad lägsta kvalitet, är sådana garantier sällsynta för kubiska maskor, och många populära implementeringar genererar inverterade (in och ut) hexes från vissa ingångar.

Mesh skapas ofta i serie på arbetsstationer, även när efterföljande beräkningar över nätet kommer att göras parallellt på superdatorer. Detta är både på grund av begränsningen att de flesta mesh-generatorer är interaktiva, och på att körtiden för meshgenerering vanligtvis är obetydlig jämfört med lösarens tid. Men om nätet är för stort för att få plats i minnet på en enstaka seriell maskin, eller om nätet måste ändras (anpassas) under simuleringen, sker maskningen parallellt.

Algebraiska metoder

Munstycksgeometri

Beräkningsnät i fysiskt utrymme

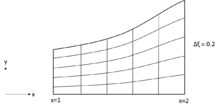
Gridgenereringen med algebraiska metoder är baserad på matematisk interpolationsfunktion . Det görs genom att använda kända funktioner i en, två eller tre dimensioner som tar godtyckligt formade områden. Beräkningsdomänen kanske inte är rektangulär, men för enkelhetens skull anses domänen vara rektangulär. Den största fördelen med metoderna är att de ger explicit kontroll över den fysiska rutnätets form och avstånd. Den enklaste proceduren som kan användas för att producera gränsanpassad beräkningsnät är normaliseringstransformationen. För ett munstycke, med den beskrivande funktionen $y=x^{2}$ kan rutnätet enkelt genereras med hjälp av enhetlig uppdelning i y -led med lika stora inkrement i x -riktning, som beskrivs av

$\xi =x\,$

$\eta ={\frac {y}{y_{\max }}}\,$

där $y_{\max }$ anger y-koordinaten för munstycksväggen. För givna värden på ( $\xi$ , $\eta$ ), kan värdena på ( $x$ , ${\displaystyle y} )$ enkelt återställas.

Metoder för differentialekvationer

Liksom algebraiska metoder används även differentialekvationsmetoder för att generera rutnät . Fördelen med att använda de partiella differentialekvationerna (PDE) är att lösningen av nätgenererande ekvationer kan utnyttjas för att generera nätet. Gridkonstruktion kan göras med alla tre klasserna av partiella differentialekvationer .

Elliptiska scheman

Elliptiska PDE:er har i allmänhet mycket smidiga lösningar som leder till jämna konturer. Med hjälp av dess jämnhet som en fördel Laplaces ekvationer helst användas eftersom jakobianen visade sig vara positiv som ett resultat av maximal princip för harmoniska funktioner . Efter omfattande arbete utfört av Crowley (1962) och Winslow (1966) på PDE:er genom att transformera fysiska domäner till beräkningsplan samtidigt som man kartlade med Poissons ekvation, Thompson et al. (1974) har arbetat mycket med elliptiska PDE:er för att generera rutnät. I Poisson-rutnätsgeneratorer utförs mappningen genom att markera de önskade rutnätspunkterna $(x,y)$ på gränsen för den fysiska domänen, med den inre punktfördelningen bestämd genom lösningen av ekvationerna nedan

$\xi _{xx}+\xi _{yy}=P(\xi ,\eta )$

$\eta _{xx}+\eta _{yy}=Q(\xi ,\eta )$

där, $(\xi ,\eta )$ är koordinaterna i beräkningsdomänen, medan P och Q är ansvariga för punktavstånd inom D. Transformering av ovanstående ekvationer i beräkningsutrymme ger en uppsättning av två elliptiska PDE av formen,

$\alpha x_{\xi \xi }-2\beta x_{\xi \eta }+\gamma x_{\eta \eta }=-I^{2}(Px_{\xi }+Qx_{\eta})$

$\alpha y_{\xi \xi }-2\beta y_{\xi \eta }+\gamma y_{\eta \eta }=-I^{2} (Py_{\xi }+Qy_{\eta })$

var

${\begin{aligned}\alpha &=x_{\eta }^{2}+y_{\eta }^{2}\\\beta &=x_{\eta }x_{\xi }+y_{\xi }y_{\eta }\\\gamma &=x_{\xi }^{2}+y_{\xi}^{2}\\I&={\frac {\delta (x, y)}{\delta (\xi ,\eta )}}=y_{\eta }x_{\xi }-y_{\xi }x_{\eta }\end{aligned}}$

Dessa ekvationssystem löses i beräkningsplanet på jämnt fördelade rutnät som ger oss ${\displaystyle (x,y)}-$ koordinaterna för varje punkt i det fysiska rummet. Fördelen med att använda elliptiska PDE:er är att lösningen kopplad till dem är jämn och det resulterande rutnätet är jämnt. Men specifikation av P och Q blir en svår uppgift, vilket lägger till dess nackdelar. Dessutom måste rutnätet beräknas efter varje tidssteg, vilket summerar till beräkningstid.

Hyperboliska scheman

Detta nätgenereringsschema är generellt tillämpligt på problem med öppna domäner som överensstämmer med den typ av PDE som beskriver det fysiska problemet. Fördelen med hyperboliska PDE:er är att de styrande ekvationerna endast behöver lösas en gång för att generera rutnät. Den initiala punktfördelningen tillsammans med de ungefärliga randvillkoren utgör den erforderliga ingången och lösningen marscheras sedan utåt. Steger och Sorenson (1980) föreslog en volymortogonalitetsmetod som använder hyperboliska PDE:er för meshgenerering. För ett 2D-problem, med tanke på att beräkningsutrymme ges av ${\displaystyle \Delta \xi =\Delta \eta =1} , ges$ inversen av Jacobian av,

$x_{\xi }y_{\eta }-x_{\eta }y_{\xi }=I$

där $I$ representerar arean i det fysiska rummet för ett givet område i beräkningsutrymmet. Den andra ekvationen länkar ortogonaliteten hos rutnätslinjer vid gränsen i det fysiska rummet som kan skrivas som

$d\xi =0=\xi _{x}\,dx+\xi _{y}\,dy.$

För att $\xi$ och $\eta$ ytor ska vara vinkelräta blir ekvationen

$x_{\xi }x_{\eta }+y_{\xi }y_{\eta }=0.$

Problemet förknippat med ett sådant ekvationssystem är specifikationen av $I$ . Dåligt val av $I$ kan leda till chock och diskontinuerlig spridning av denna information genom nätet. Medan mesh är ortogonalt genereras mycket snabbt vilket kommer ut som en fördel med denna metod.

Paraboliska scheman

Lösningstekniken liknar den för hyperboliska PDE:er genom att föra lösningen bort från den initiala dataytan som uppfyller gränsvillkoren i slutet. Nakamura (1982) och Edwards (1985) utvecklade de grundläggande idéerna för generering av paraboliska rutnät. Idén använder antingen Laplace eller Poissons ekvation och behandlar särskilt de delar som styr elliptiskt beteende. De initiala värdena ges som koordinaterna för punkten längs ytan $\eta =0$ och de frammatande lösningarna till den yttre ytan av objektet som uppfyller gränsvillkoren längs $\xi$ kanter.

Kontroll av rutnätsavståndet har inte föreslagits förrän nu. Nakamura och Edwards, rutnätskontroll utfördes med hjälp av olikformigt avstånd. Genereringen av parabolnät uppvisar en fördel jämfört med generering av hyperboliska rutnät att inga stötar eller diskontinuiteter uppstår och nätet är relativt jämnt. Specifikationerna för initiala värden och val av stegstorlek för att styra rutnätspunkterna är dock tidskrävande, men dessa tekniker kan vara effektiva när förtrogenhet och erfarenhet erhålls.

Varierande metoder

Denna metod inkluderar en teknik som minimerar rutnätets jämnhet, ortogonalitet och volymvariation. Denna metod utgör en matematisk plattform för att lösa problem med nätgenerering. I denna metod genereras ett alternativt rutnät av ett nytt nät efter varje iteration och beräkning av rutnätshastigheten med hjälp av en bakåtskillnadsmetod. Denna teknik är kraftfull med nackdelen att det krävs ansträngning för att lösa ekvationerna relaterade till rutnät. Ytterligare arbete behövde göras för att minimera integralerna som kommer att minska CPU-tiden.

Ostrukturerad nätgenerering

Huvudvikten med detta schema är att det tillhandahåller en metod som genererar nätet automatiskt. Med denna metod segmenteras galler i block enligt elementets yta och en struktur tillhandahålls för att säkerställa lämplig anslutning. För att tolka dataflödeslösaren används . När ett ostrukturerat schema används är huvudintresset att uppfylla användarens efterfrågan och en nätgenerator används för att utföra denna uppgift. Informationslagringen i ett strukturerat schema är cell till cell istället för rutnät till rutnät och därför behövs mer minnesutrymme. På grund av slumpmässig cellplacering lösningseffektiviteten i ostrukturerad mindre jämfört med det strukturerade schemat.

Vissa punkter är nödvändiga att ha i åtanke vid tidpunkten för nätkonstruktion . Rutnätspunkten med hög upplösning skapar svårigheter för både strukturerade och ostrukturerade. Till exempel, i fallet med gränsskikt , producerar strukturerat schema ett långsträckt rutnät i flödesriktningen. Å andra sidan kräver ostrukturerade rutnät en högre celltäthet i gränsskiktet eftersom cellen måste vara så liksidig som möjligt för att undvika fel.

Vi måste identifiera vilken information som krävs för att identifiera cellen och alla grannar till cellen i beräkningsnätet . Vi kan välja att lokalisera de godtyckliga punkterna var som helst vi vill för det ostrukturerade rutnätet. Ett punktinsättningsschema används för att infoga punkterna oberoende och cellanslutningen bestäms. Detta tyder på att punkten identifieras när de sätts in. Logik för att etablera ny anslutning bestäms när punkterna har infogats. Data som bildar rutnätspunkt som identifierar rutnätscell behövs. När varje cell bildas numreras den och punkterna sorteras. Dessutom behövs granncellsinformation.

Adaptivt rutnät

Ett problem med att lösa partiella differentialekvationer med tidigare metoder är att rutnätet är konstruerat och punkterna fördelas i den fysiska domänen innan detaljerna i lösningen är kända. Så rutnätet kan eller kanske inte är det bästa för det givna problemet.

Adaptiva metoder används för att förbättra noggrannheten i lösningarna. Den adaptiva metoden hänvisas till som 'h'-metoden om nätförfining används, 'r'-metoden om antalet rutnätspunkter är fast och inte omfördelas och 'p' om lösningsordningen ökas i finita elementteori. De flerdimensionella problemen med användning av equidistribution-schemat kan åstadkommas på flera sätt. De enklaste att förstå är Poisson Grid Generators med kontrollfunktion baserad på jämnfördelning av viktfunktionen med diffusionsinställningen som en multipel av önskad cellvolym. Likfördelningsschemat kan också tillämpas på det ostrukturerade problemet. Problemet är att anslutningen hämmar om nätpunktens rörelse är mycket stor.

Stadigt flöde och den tidsexakta flödesberäkningen kan lösas genom denna adaptiva metod. Gallret förfinas och efter ett förutbestämt antal iterationer för att anpassa det i ett problem med konstant flöde. Rutnätet kommer att sluta anpassa sig till ändringarna när lösningen konvergerar. Med tiden krävs noggrann fallkoppling av de partiella differentialekvationerna för det fysiska problemet och de som beskriver rutnätets rörelse.

Celltopologi

Vanligtvis är cellerna polygonala eller polyedriska och bildar ett nät som delar upp domänen. Viktiga klasser av tvådimensionella element inkluderar trianglar (enkla) och fyrhörningar (topologiska kvadrater). I tredimensioner är de vanligaste cellerna tetraedrar (simplicerade) och hexaedrar (topologiska kuber). Enkla maskor kan ha vilken dimension som helst och inkluderar trianglar (2D) och tetraedrar (3D) som viktiga instanser. Kubiska maskor är den pan-dimensionella kategorin som inkluderar fyrhjulingar (2D) och hex (3D). I 3D visas 4-sidiga pyramider och 3-sidiga prismor i konforma maskor av blandad celltyp.

Celldimension

Nätet är inbäddat i ett geometriskt utrymme som vanligtvis är två- eller tredimensionellt , även om dimensionen ibland ökas med en genom att lägga till tidsdimensionen. Högdimensionella maskor används i nischsammanhang. Endimensionella maskor är också användbara. En betydande kategori är ytmaskor, som är 2D-nät inbäddade i 3D för att representera en krökt yta.

Dualitet

Dubbla grafer har flera roller i meshing. Man kan göra ett polyedriskt Voronoi-diagramnät genom att dualisera ett Delaunay-triangulerings- förenklat nät. Man kan skapa ett kubiskt nät genom att generera ett arrangemang av ytor och dualisera skärningsdiagrammet; se rumsligt vridkontinuum . Ibland används både det primära nätet och dess dubbla nät i samma simulering; se Hodge stjärnoperatör . Detta uppstår från fysik som involverar divergens- och curl -operatorer (matematik), såsom flöde och virvel eller elektricitet och magnetism , där en variabel naturligt lever på de primära ytorna och dess motsvarighet på de dubbla ytorna.

Nättyp efter användning

Tredimensionella nät skapade för finita elementanalys måste bestå av tetraedrar , pyramider , prismor eller hexaedrar . De som används för metoden med ändlig volym kan bestå av godtyckliga polyedrar . De som används för ändliga differensmetoder består av bitvis strukturerade arrayer av hexaedrar som kallas flerblocksstrukturerade maskor. 4-sidiga pyramider är användbara för att konformt ansluta hexes till tets. 3-sidiga prismor används för gränsskikt som överensstämmer med ett tet-nät längst in i föremålet.

Ytmaskor är användbara i datorgrafik där objektens ytor reflekterar ljus (även spridning under ytan ) och ett fullständigt 3D-nät inte behövs. Ytnät används också för att modellera tunna föremål som plåt i biltillverkning och byggnadsexteriörer inom arkitektur. Höga (t.ex. 17) dimensionella kubiska maskor är vanliga inom astrofysik och strängteori .

Matematisk definition och varianter

Vad är den exakta definitionen av ett nät? Det finns inte en universellt accepterad matematisk beskrivning som gäller i alla sammanhang. Vissa matematiska objekt är dock tydligt maskor: ett förenklat komplex är ett nätverk som består av förenklingar. De flesta polyedriska (t.ex. kubiska) maskor är konforma, vilket betyder att de har cellstrukturen av ett CW-komplex , en generalisering av ett förenklat komplex . Ett nät behöver inte vara enkelt eftersom en godtycklig delmängd av noder i en cell inte nödvändigtvis är en cell: t.ex. definierar tre noder i en quad inte en cell. Men två celler skär varandra vid cellerna: t.ex. en quad har ingen nod i sitt inre. Skärningen mellan två celler kan vara flera celler: t.ex. kan två quads dela två kanter. En korsning med mer än en cell är ibland förbjuden och sällan önskvärd; Målet med vissa nätförbättringstekniker (t.ex. kuddar) är att ta bort dessa konfigurationer. I vissa sammanhang skiljer man mellan ett topologiskt nät och ett geometriskt nät vars inbäddning uppfyller vissa kvalitetskriterier.

Viktiga nätvarianter som inte är CW-komplex inkluderar icke-konforma nät där cellerna inte möts strikt ansikte mot ansikte, men cellerna delar upp domänen. Ett exempel på detta är en oktree , där en elementyta kan delas upp av intilliggande elements ytor. Sådana maskor är användbara för flödesbaserade simuleringar. I översatta rutnät finns det flera konforma mesh som överlappar geometriskt och inte delar upp domänen; se t.ex. Overflow, OVERset grid FLOW solver . Så kallade meshless eller meshfree metoder använder sig ofta av viss mesh-liknande diskretisering av domänen och har basfunktioner med överlappande stöd. Ibland skapas ett lokalt nät nära varje simuleringspunkt för frihetsgrad, och dessa nät kan överlappa varandra och vara icke-konforma med varandra.

Implicita trianguleringar är baserade på ett deltakomplex: för varje triangel längden på dess kanter och en limningskarta mellan ytkanterna. (snälla utöka)

Högklassiga element

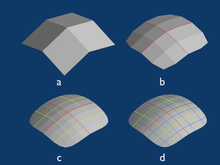
Många maskor använder linjära element, där mappningen från det abstrakta till det realiserade elementet är linjär, och meshkanterna är raka segment. Polynomavbildningar av högre ordning är vanliga, särskilt kvadratiska. Ett primärt mål för element av högre ordning är att mer exakt representera domängränsen, även om de har precisionsfördelar även i det inre av nätet. En av motiven för kubiska maskor är att linjära kubiska element har några av samma numeriska fördelar som kvadratiska enkla element. I för isogeometrisk analys använder nätcellerna som innehåller domängränsen CAD-representationen direkt istället för en linjär eller polynom approximation.

Mesh förbättring

Se även: Delaunay-förfining

Att förbättra ett nät involverar att ändra dess diskreta anslutning, den kontinuerliga geometriska positionen för dess celler, eller båda. För diskreta ändringar, för enkla element byter man kanter och infogar/tar bort noder. Samma typer av operationer görs för kubiska (quad/hex) maskor, även om det finns färre möjliga operationer och lokala förändringar har globala konsekvenser. Till exempel, för ett hexaedriskt nät, skapar en sammanslagning av två noder celler som inte är hexes, men om diagonalt motsatta noder på en fyrhörning slås samman och detta fortplantas till att kollapsa en hel ansiktsansluten kolumn av hexes, kommer alla återstående celler fortfarande att vara hexar. I adaptiv nätförfining delas element (h-förfining) i områden där funktionen som beräknas har en hög gradient. Maskor är också förgrovade, vilket tar bort element för effektivitet. Multigrid -metoden gör något som liknar förfining och förgrovning för att påskynda den numeriska lösningen, men utan att faktiskt ändra nätet.

För kontinuerliga förändringar flyttas noder, eller de högre dimensionella ytorna flyttas genom att ändra polynomordningen för element. Att flytta noder för att förbättra kvaliteten kallas "utjämning" eller "r-förfining" och att öka ordningen på element kallas "p-förfining". Noder flyttas också i simuleringar där formen på objekt förändras över tiden. Detta försämrar formen på elementen. Om objektet deformeras tillräckligt, maskas hela objektet ihop och den nuvarande lösningen mappas från det gamla nätet till det nya nätet.

Forskargemenskap

Utövare

Fältet är mycket tvärvetenskapligt, med bidrag som finns inom matematik , datavetenskap och teknik . Meshing R&D kännetecknas av ett lika stort fokus på diskret och kontinuerlig matematik och beräkning, som med beräkningsgeometri , men i motsats till grafteori (diskret) och numerisk analys (kontinuerlig). Meshgenerering är bedrägligt svårt: det är lätt för människor att se hur man skapar ett nät av ett visst objekt, men svårt att programmera en dator att fatta bra beslut för godtycklig inmatning a priori. Det finns en oändlig variation av geometri som finns i naturen och konstgjorda föremål. Många forskare i nätgenerering var första användare av nät. Mesh-generering fortsätter att få stor uppmärksamhet, stöd och finansiering eftersom den mänskliga tiden för att skapa ett nät försämrar tiden för att sätta upp och lösa beräkningen när nätet är färdigt. Detta har alltid varit situationen sedan numerisk simulering och datorgrafik uppfanns, för allt eftersom datorhårdvara och enkel ekvationslösningsmjukvara har förbättrats, har människor dragits till större och mer komplexa geometriska modeller i en strävan efter större trohet, vetenskaplig insikt och konstnärligt uttryck.

Tidskrifter

Meshing research publiceras i ett brett spektrum av tidskrifter. Detta är i linje med den tvärvetenskapliga karaktären hos den forskning som krävs för att göra framsteg, och även det stora utbudet av applikationer som använder mesh. Cirka 150 mesh-publikationer dyker upp varje år i 20 tidskrifter, med högst 20 publikationer i en och samma tidskrift. Det finns ingen tidskrift vars primära ämne är meshing. De tidskrifter som publicerar minst 10 meshing papers per år är i fetstil.

• Framsteg inom teknisk programvara
• American Institute of Aeronautics and Astronautics Journal (AIAAJ)
• Algoritmik
• Applied Computational Electromagnetics Society Journal
• Tillämpad numerisk matematik
• Astronomi och beräkningar
• Beräkningsgeometri: teori och tillämpningar
• Datorstödd design , ofta inklusive ett specialnummer ägnat åt utökade artiklar från IMR (se konferenser nedan)
• Datorstödd geometrisk design (CAGD)
• Computer Graphics Forum (Eurographics)
• Datormetoder i tillämpad mekanik och teknik
• Diskret och beräkningsgeometri
• Engineering med datorer
• Finita element i analys och design
• International Journal for Numerical Methods in Engineering (IJNME)
• International Journal for Numerical Methods in Fluids
• International Journal for Numerical Methods in Biomedical Engineering
• International Journal of Computational Geometry & Applications
• Journal of Computational Physics (JCP)
• Tidskrift om numerisk analys
• Journal on Scientific Computing (SISC)
• Transaktioner på grafik (ACM TOG)
• Transaktioner på matematisk programvara (ACM TOMS)
• Transaktioner på visualisering och datorgrafik (IEEE TVCG)
• Lecture Notes in Computational Science and Engineering (LNCSE)
• Beräkningsmatematik och matematisk fysik (CMMP)

Konferenser

(Konferenser vars primära ämne är samverkan är i fetstil. )

• Aerospace Sciences Meeting AIAA (15 meshing talks/papers)
• Kanadensisk konferens om beräkningsgeometri CCCG
• CompIMAGE: International Symposium Computational Modeling of Objects Represented in Images
• Computational Fluid Dynamics Conference AIAA
• Computational Fluid Dynamics Conference ECCOMAS
• Computational Science & Engineering CS&E
• Konferens om numerisk nätgenerering ISGG
• Eurographics Annual Conference (Eurgraphics)] (förhandlingar i Computer Graphics Forum)
• Geometrisk och fysisk modellering SIAM
• Internationell konferens om isogeometrisk analys IGA
• Internationellt symposium om beräkningsgeometri SoCG
• Numerisk geometri, Grid Generation och Scientific Computing (NUMGRID) (förfaranden i föreläsningsanteckningar i Computational Science and Engineering)
• SIAM International Meshing Roundtable (SIAM IMR) . En oberoende årlig konferens från 1992-2021 och en SIAM-workshop parallellt med SIAM PP eller SIAM CS&E sedan 2022. Refererade förfaranden.
• SIGGRAPH (förfaranden i ACM Transactions on Graphics )
• Symposium on Geometry Processing SGP ( Eurographics ) (förhandlingar i Computer Graphics Forum)
• World Congress on Engineering

Workshops

Workshops vars primära ämne är samverkan är i fetstil.

• Konferens om geometri: teori och tillämpningar CGTA
• European Workshop on Computational Geometry EuroCG
• Höstens workshop om beräkningsgeometri
• Finita element i vätskor FEF
• MeshTrends Symposium (växelvis i WCCM eller USNCCM)
• Polytopala elementmetoder i matematik och teknik
• Tetraederverkstad

Se även

• Delaunay triangulering
• Fortunes algoritm
• Rutnätsklassificering
• Mesh-parameterisering
• Meshfria metoder
• Generering av parallellnät
• Principer för nätgenerering
• Polygonnät
• Vanligt rutnät
• Rupperts algoritm
• Sträckt rutnätsmetod
• Tessellation
• Typer av mesh
• Ostrukturerat rutnät

Bibliografi

•   Edelsbrunner, Herbert (2001), "Geometry and Topology for Mesh Generation", Applied Mechanics Reviews , Cambridge University Press, 55 ( 1): B1–B2, Bibcode : 2002ApMRv..55B...1E , doi : 10.1115/1.1445302 ISBN 978-0-521-79309-4 .
•   Frey, Pascal Jean; George, Paul-Louis (2000), Mesh Generation: Application to Finite Elements , Hermes Science, ISBN 978-1-903398-00-5 .
• P. Smith och SS Sritharan (1988), "Theory of Harmonic Grid Generation" (PDF) , Complex Variables , 10 (4): 359–369, doi : 10.1080/17476938808814314
• SS Sritharan (1992), "Theory of Harmonic Grid Generation-II", Applicable Analysis , 44 (1): 127–149, doi : 10.1080/00036819208840072
• Thompson, JF ; Warsi, ZUA; Mastin, CW (1985), Numerical Grid Generation: Foundations and Applications , North-Holland , Elsevier .
• CGAL The Computational Geometry Algoritms Library
• Oden, J. Tinsley; Cho, JR (1996), "Adaptive hpq-Finite Element Methods of Hierarchical Models for Plate- and Shell-like Structures", Computer Methods in Applied Mechanics and Engineering , 136 (3): 317–345, Bibcode : 1996CMAME.136. .317O , doi : 10.1016/0045-7825(95)00986-8
•   Steven J. Owen (1998), A Survey of Unstructured Mesh Generation Technology , International Meshing Roundtable, s. 239–267, S2CID 2675840
•    Shimada, Kenji; Gossard, David C. (1995). Bubble Mesh: Automatiserad triangulär meshing av icke-grenrörsgeometri genom sfärförpackning . ACM Symposium on Solid Modeling and Applications, SMA. ACM. sid. 409-419 . doi : 10.1145/218013.218095 . ISBN 0-89791-672-7 . S2CID 1282987 .

•   Jan Brandts, Sergey Korotov, Michal Krizek: "Simplicial Partitions with Applications to the Finite Element Method", Springer Monographs in Mathematics, ISBN 978-3030556761 (2020). url=" https://www.springer.com/gp/book/9783030556761 "
• Grid Generation Methods - Liseikin, Vladimir D.

externa länkar

• Periodiska systemet för de ändliga elementen
• Litteratur om Mesh Generation
• Konferenser, Workshops, Summerschools

Mesh generatorer

Många kommersiella produktbeskrivningar betonar simulering snarare än meshing-tekniken som möjliggör simulering.

• Listor över nätgeneratorer (extern):
  • Mesh-generatorer för gratis/öppen källkod
  • Public domain och kommersiella mesh-generatorer
• ANSA Pre-processor
• ANSYS
• CD-adapco och Siemens DISW
• Comet Solutions
• CGAL Computational Geometry Algoritms Library
  • Mesh generation
    • 2D-konforma trianguleringar och maskor
    • 3D Mesh Generation
• ALN
• Gmsh
• Hextrema maskor
• MeshLab
• MSC programvara
• Omega_h Tri/Tet-anpassningsförmåga
• Open FOAM Mesh generering och konvertering
• Salome Mesh -modul
• TetGen
• TetWild
• TRIANGLE Mesh generation och Delaunay triangulering

Multi-domän partitionerade mesh generatorer

Dessa verktyg genererar de partitionerade maskor som krävs för modellering av ändliga element i flera material.

• MDM (Multiple Domain Meshing) genererar ostrukturerade tetraedriska och hexaedriska nät för en sammansatt domän som består av heterogena material, automatiskt och effektivt
• QMDM (Quality Multi-Domain Meshing) producerar högkvalitativa, ömsesidigt konsekventa triangulära ytmaskor för flera domäner
• QMDMNG , (Quality Multi-Domain Meshing with No Gap), producerar ett kvalitetsnät med var och en ett tvådimensionellt grenrör och inget mellanrum mellan två intilliggande maskor.
• SOFA_mesh_partitioning_tools genererar partitionerade tetraedriska nät för multi-material FEM, baserat på CGAL.

Artiklar

• Another Fine Mesh, MeshTrends Blog, Pointwise
• Mesh Generation & Grid Generation på webben
• Mesh Generation-grupp på LinkedIn

Forskargrupper och människor

• Mesh Generation människor på Google Scholar
• David Bommes, Computer Graphics Group, University of Bern
• David Eppsteins Geometry in Action, Mesh Generation
• Jonathan Shewchuks Meshing and Triangulation in Graphics, Engineering and Modeling
• Scott A. Mitchell
• Robert Schneiders

Modeller och mesh

Användbara modeller (ingångar) och maskor (utgångar) för att jämföra mesh-algoritmer och maskor.

• HexaLab har modeller och maskor som har publicerats i forskningsartiklar, rekonstruerade eller från originalartikeln.
• Princeton Shape Benchmark
• Shape Retrieval Contest SHREC har olika modeller varje år, t.ex.
  • Shape Retrieval Contest of Non-rigid 3D Watertight Meshes 2011
• Thingi10k meshed modeller från Thingiverse

CAD-modeller

Modelleringsmotorer kopplade till mesh-genereringsprogramvara för att representera domängeometrin.

• ACIS från Spatial
• Öppna Cascade

Mesh filformat

Vanliga (utdata) filformat för att beskriva maskor.

• NetCDF
• Genesis/Exodus
• XDMF
• VTK/VTU
• MEDIT
• MED/Salome
• Gmsh
• ANSYS mesh
• AV
• Wavefront OBJ
• LAGER
• STL
• meshio kan konvertera mellan alla ovanstående format.

Mesh-visualiserare

• Blandare
• Mesh Viewer
• Paraview

Handledningar

• Cubit handledningar