Strukturanalys

Strukturanalys är en gren av solid mekanik som använder förenklade modeller för fasta ämnen som stänger, balkar och skal för tekniskt beslutsfattande. Dess huvudsakliga syfte är att fastställa effekten av laster på de fysiska strukturerna och deras komponenter . Till skillnad från elasticitetsteorin är modellerna som används i strukturanalys ofta differentialekvationer i en rumslig variabel. Strukturer som är föremål för denna typ av analys omfattar allt som ska tåla belastningar, såsom byggnader, broar, flygplan och fartyg. Strukturanalys använder idéer från tillämpad mekanik , materialvetenskap och tillämpad matematik för att beräkna en strukturs deformationer , inre krafter , spänningar , stödreaktioner, hastighet, accelerationer och stabilitet . Resultaten av analysen används för att verifiera en strukturs lämplighet för användning, vilket ofta utesluter fysiska tester . Strukturanalys är således en viktig del av den tekniska designen av strukturer .

Strukturer och laster

I samband med strukturanalys avser en struktur en kropp eller system av sammankopplade delar som används för att bära upp en last. Viktiga exempel relaterade till anläggningsteknik inkluderar byggnader, broar och torn; och inom andra grenar av ingenjörskonst, är fartygs- och flygplansramar, tankar, tryckkärl, mekaniska system och elektriska bärande strukturer viktiga. För att designa en struktur måste en ingenjör ta hänsyn till dess säkerhet, estetik och användbarhet, samtidigt som ekonomiska och miljömässiga begränsningar beaktas. Andra grenar av ingenjörskonst arbetar på en mängd olika icke-byggnadskonstruktioner .

Klassificering av strukturer

Ett strukturellt system är kombinationen av strukturella element och deras material. Det är viktigt för en byggnadsingenjör att kunna klassificera en struktur efter antingen dess form eller funktion, genom att känna igen de olika elementen som utgör strukturen. De strukturella elementen som styr de systemiska krafterna genom materialen är inte bara såsom en vevstake, en fackverk, en balk eller en pelare, utan också en kabel, en båge, en kavitet eller kanal, och till och med en vinkel, en ytstruktur , eller en ram.

Massor

När dimensionskravet för en konstruktion väl har definierats, blir det nödvändigt att bestämma de belastningar konstruktionen måste bära. Konstruktionsdesign börjar därför med att specificera laster som verkar på strukturen. Konstruktionsbelastningen för en konstruktion anges ofta i byggregler . Det finns två typer av koder: allmänna byggregler och designkoder, ingenjörer måste uppfylla alla kodens krav för att strukturen ska förbli tillförlitlig.

Det finns två typer av belastningar som konstruktionsteknik måste möta i konstruktionen. Den första typen av laster är döda laster som består av vikterna av de olika konstruktionselementen och vikten av eventuella föremål som är permanent fästa vid strukturen. Till exempel pelare, balkar, balkar, golvplattan, tak, väggar, fönster, VVS, elektriska inventarier och andra diverse tillbehör. Den andra typen av laster är levande laster som varierar i storlek och plats. Det finns många olika typer av levande laster som byggnadslaster, motorvägsbrolaster, järnvägsbrolaster, slaglaster, vindlaster, snölaster, jordbävningslaster och andra naturliga laster.

analytiska metoder

För att utföra en noggrann analys måste en konstruktionsingenjör fastställa information såsom strukturella belastningar , geometri , stödförhållanden och materialegenskaper. Resultaten av en sådan analys inkluderar vanligtvis stödreaktioner, spänningar och förskjutningar . Denna information jämförs sedan med kriterier som anger förutsättningarna för misslyckande. Avancerad strukturanalys kan undersöka dynamisk respons , stabilitet och icke-linjärt beteende. Det finns tre tillvägagångssätt för analysen: materialmekaniken ( även känd som materialstyrka), elasticitetsteorin (vilket faktiskt är ett specialfall av det mer allmänna området för kontinuummekanik ) och tillvägagångssättet med finita element . De två första använder sig av analytiska formuleringar som använder mestadels enkla linjära elastiska modeller, vilket leder till lösningar i sluten form, och som ofta kan lösas för hand. Finita elementmetoden är faktiskt en numerisk metod för att lösa differentialekvationer genererade av teorier om mekanik som elasticitetsteori och materialstyrka. Den finita elementmetoden beror dock starkt på datorers processorkraft och är mer tillämpbar på strukturer av godtycklig storlek och komplexitet.

Oavsett tillvägagångssätt är formuleringen baserad på samma tre grundläggande relationer: jämvikt , konstitutiv och kompatibilitet . Lösningarna är ungefärliga när någon av dessa relationer endast är ungefärligen uppfyllda, eller endast en approximation av verkligheten.

Begränsningar

Varje metod har anmärkningsvärda begränsningar. Metoden för mekanik av material är begränsad till mycket enkla strukturella element under relativt enkla belastningsförhållanden. De strukturella elementen och de tillåtna belastningsförhållandena är dock tillräckliga för att lösa många användbara tekniska problem. Teorin om elasticitet tillåter lösningen av strukturella element av allmän geometri under allmänna belastningsförhållanden, i princip. Analytisk lösning är dock begränsad till relativt enkla fall. Lösningen av elasticitetsproblem kräver också lösningen av ett system av partiella differentialekvationer, vilket är avsevärt mer matematiskt krävande än lösningen av materialmekanikproblem, som på sin höjd kräver lösningen av en vanlig differentialekvation. Den finita elementmetoden är kanske den mest restriktiva och mest användbara på samma gång. Denna metod i sig förlitar sig på andra strukturella teorier (som de andra två som diskuteras här) för att ekvationer ska lösas. Det gör det dock generellt möjligt att lösa dessa ekvationer, även med mycket komplexa geometri- och belastningsförhållanden, med begränsningen att det alltid finns något numeriskt fel. Effektiv och tillförlitlig användning av denna metod kräver en gedigen förståelse för dess begränsningar.

Materialstyrka metoder (klassiska metoder)

Den enklaste av de tre metoderna som diskuteras här, metoden för materialmekanik, är tillgänglig för enkla konstruktionselement som utsätts för specifika belastningar såsom axiellt belastade stänger, prismatiska balkar i ett tillstånd av ren böjning och cirkulära axlar utsatta för vridning. Lösningarna kan under vissa förhållanden överlagras med hjälp av superpositionsprincipen för att analysera ett element som genomgår kombinerad belastning. Lösningar för speciella fall finns för vanliga konstruktioner som tunnväggiga tryckkärl.

För analys av hela system kan detta tillvägagångssätt användas tillsammans med statik, vilket ger upphov till metoden för sektioner och metoden för fogar för fackverksanalys, momentfördelningsmetod för små stela ramar och portalram och konsolmetoden för stora stela ramar . Förutom momentdistribution, som togs i bruk på 1930-talet, utvecklades dessa metoder i sina nuvarande former under andra hälften av artonhundratalet. De används fortfarande för små strukturer och för preliminär design av stora strukturer.

Lösningarna är baserade på linjär isotrop infinitesimal elasticitet och Euler-Bernoullis strålteori. Med andra ord innehåller de antagandena (bland annat) att de aktuella materialen är elastiska, att spänning är linjärt relaterad till töjning, att materialet (men inte strukturen) beter sig identiskt oavsett riktning på den pålagda lasten, att alla deformationer är små och att strålarna är långa i förhållande till deras djup. Som med alla förenklade antaganden inom teknik, ju mer modellen avviker från verkligheten, desto mindre användbart (och farligare) blir resultatet.

Exempel

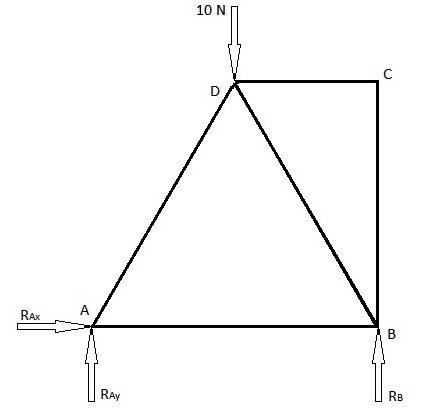
Det finns 2 vanliga metoder för att hitta fackverkselementets krafter, nämligen metoden för fogar och metoden för sektioner. Nedan följer ett exempel som löses med båda dessa metoder. Det första diagrammet nedan är det presenterade problemet för vilket fackverkselementets krafter måste hittas. Det andra diagrammet är belastningsdiagrammet och innehåller reaktionskrafterna från lederna.

Eftersom det finns en stiftled vid A kommer den att ha 2 reaktionskrafter. En i x-riktningen och den andra i y-riktningen. Vid punkt B finns en rullfog och därmed endast 1 reaktionskraft i y-riktningen. Om man antar att dessa krafter är i sina respektive positiva riktningar (om de inte är i de positiva riktningarna kommer värdet att vara negativt).

Eftersom systemet är i statisk jämvikt är summan av krafter i valfri riktning noll och summan av moment runt vilken punkt som helst är noll. Därför kan storleken och riktningen av reaktionskrafterna beräknas.

\summa M_{A}=0=-10*1+2*R_{B}\Högerpil R_{B}=5

\sum F_{y}=0=R_{Ay}+R_{B}-10\Rightarrow R_{Ay}= 5

\sum F_{x}=0=R_{Ax}

Metod för leder

Denna typ av metod använder kraftbalansen i x- och y-riktningarna vid var och en av lederna i fackverksstrukturen.

Vid A,

\sum F_{y}=0=R_{Ay}+ F_{AD}\sin(60)=5+F_{AD}{\frac {\sqrt {3}}{2}}\Rightarrow F_{AD}=-{\frac {10}{\sqrt {3} }}

\sum F_{x} =0=R_{Ax}+F_{AD}\cos(60)+F_{AB}=0-{\frac {10}{\sqrt {3}}}{\frac {1}{2}}+ F_{AB}\Rightarrow F_{AB}={\frac {5}{\sqrt {3}}}

Vid D,

\sum F_{y}=0=-10-F_{AD}\sin(60)-F_{BD}\sin(60)=-10-\left(-{\frac {10}{\ sqrt {3}}}\right){\frac {\sqrt {3}}{2}}-F_{BD}{\frac {\sqrt {3}}{2}}\Rightarrow F_{BD}=- {\frac {10}{\sqrt {3}}}

\sum F_{x}=0=-F_{AD}\cos(60)+F_{BD}\cos(60)+F_{CD}= -{\frac {10}{\sqrt {3}}}{\frac {1}{2}}+{\frac {10}{\sqrt {3}}}{\frac {1}{2}} +F_{CD}\Rightarrow F_{CD}=0

Vid C,

\sum F_{y}=0=-F_{BC}\Högerpil F_{BC}=0

Även om krafterna i vart och ett av fackverkselementen hittas, är det en god praxis att verifiera resultaten genom att slutföra de återstående kraftbalanserna.

\sum F_{x}=-F_{CD}=-0=0\Högerpil verifierad

På B,

\sum F_{y}= R_{B}+F_{BD}\sin(60)+F_{BC}=5+\left(-{\frac {10}{\sqrt {3}}}\right){\frac {\sqrt { 3}}{2}}+0=0\Högerpil verifierad

\sum F_{x}=-F_{AB}-F_{BD}\cos(60)={\frac {5}{\sqrt {3}}}-{\frac {10}{\sqrt {3}}}{\frac {1}{2}}=0\Högerpil verifierad

Metod för sektioner

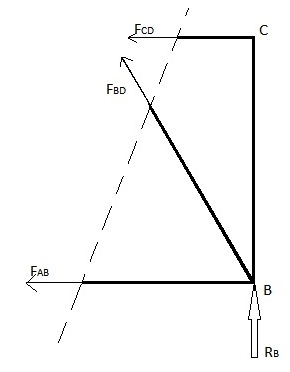
Denna metod kan användas när fackverkselementets krafter av endast ett fåtal element återfinns. Denna metod används genom att införa en enda rak linje som skär genom elementet vars kraft måste beräknas. Denna metod har emellertid en begränsning genom att skärlinan kan passera genom maximalt endast 3 delar av fackverksstrukturen. Denna begränsning beror på att denna metod använder kraftbalanserna i x- och y-riktningen och momentbalansen, vilket ger maximalt 3 ekvationer för att hitta maximalt 3 okända fackverkselementkrafter genom vilka detta snitt görs. Hitta krafterna FAB, FBD och FCD i exemplet ovan

Metod 1: Ignorera den högra sidan

Truss Structure Analysis, Method of Sections Left2.jpg

\sum M_{D}=0=-5*1+{\sqrt {3}}*F_{AB }\Rightarrow F_{AB}={\frac {5}{\sqrt {3}}}

\sum F_{y}=0=R_{Ay}-F_{BD}\sin(60)-10=5-F_{BD}{\frac {\ sqrt {3}}{2}}-10\Rightarrow F_{BD}=-{\frac {10}{\sqrt {3}}}

\sum F_{x}=0=F_{AB}+F_{BD}\cos(60)+F_ {CD}={\frac {5}{\sqrt {3}}}-{\frac {10}{\sqrt {3}}}{\frac {1}{2}}+F_{CD}\Rightarrow F_{CD}=0

Metod 2: Ignorera vänster sida

Truss Structure Analysis, Method of Sections Right2.jpg

\sum M_{B}=0={\sqrt {3}}*F_{CD}\Rightarrow F_{CD}=0

\sum F_{y}=0=F_{BD}\sin(60 )+R_{B}=F_{BD}{\frac {\sqrt {3}}{2}}+5\Rightarrow F_{BD}=-{\frac {10}{\sqrt {3}}}

\sum F_{ x}=0=-F_{AB}-F_{BD}\cos(60)-F_{CD}=-F_{AB}-\left(-{\frac {10}{\sqrt {3}}} \right){\frac {1}{2}}-0\Rightarrow F_{AB}={\frac {5}{\sqrt {3}}}

Fackverkselementens krafter i de återstående elementen kan hittas genom att använda ovanstående metod med en sektion som går genom de återstående elementen.

Elasticitetsmetoder

Elasticitetsmetoder är generellt tillgängliga för ett elastiskt fast material av vilken form som helst. Individuella delar såsom balkar, pelare, axlar, plattor och skal kan modelleras. Lösningarna härleds från ekvationerna för linjär elasticitet . Elasticitetsekvationerna är ett system med 15 partiella differentialekvationer. På grund av den inblandade matematikens natur får analytiska lösningar endast produceras för relativt enkla geometrier. För komplexa geometrier är en numerisk lösningsmetod som finita elementmetoden nödvändig.

Metoder som använder numerisk approximation

Det är vanligt att använda ungefärliga lösningar av differentialekvationer som grund för strukturanalys. Detta görs vanligtvis med hjälp av numeriska approximationstekniker. Den vanligaste numeriska approximationen i strukturanalys är Finita Element-metoden .

Finita elementmetoden approximerar en struktur som en sammansättning av element eller komponenter med olika former av koppling mellan dem och vars element har en tillhörande styvhet. Således modelleras ett kontinuerligt system såsom en platta eller skal som ett diskret system med ett ändligt antal element sammankopplade vid ändligt antal noder och den totala styvheten är resultatet av tillägget av styvheten hos de olika elementen. Beteendet hos enskilda element kännetecknas av elementets styvhet (eller flexibilitet) relation. Sammansättningen av de olika styvheterna till en huvudstyvhetsmatris som representerar hela strukturen leder till systemets styvhet eller flexibilitetsrelation. För att fastställa styvheten (eller flexibiliteten) för ett visst element kan vi använda mekaniken i material för enkla endimensionella stångelement och elasticitetsmetoden för mer komplexa två- och tredimensionella element. Den analytiska och beräkningsmässiga utvecklingen sker bäst genomgående med hjälp av matrisalgebra som löser partiella differentialekvationer .

Tidiga tillämpningar av matrismetoder tillämpades på ledade ramverk med fackverks-, balk- och pelarelement; senare och mer avancerade matrismetoder, kallade " finita elementanalys ", modellerar en hel struktur med en-, två- och tredimensionella element och kan användas för ledade system tillsammans med kontinuerliga system som ett tryckkärl , plattor , skal och tredimensionella fasta ämnen. Kommersiell datorprogramvara för strukturell analys använder vanligtvis matrisfinita elementanalys, som ytterligare kan klassificeras i två huvudmetoder: förskjutnings- eller styvhetsmetoden och kraft- eller flexibilitetsmetoden . Styvhetsmetoden är den överlägset mest populära tack vare dess enkla implementering såväl som formuleringen för avancerade applikationer. Tekniken med ändliga element är nu sofistikerad nog att hantera nästan alla system så länge som tillräcklig datorkraft finns tillgänglig. Dess tillämpbarhet inkluderar, men är inte begränsad till, linjär och icke-linjär analys, fasta och flytande interaktioner, material som är isotropa, ortotropa eller anisotropa och externa effekter som är statiska, dynamiska och miljöfaktorer. Detta innebär dock inte att den beräknade lösningen automatiskt kommer att vara tillförlitlig eftersom mycket beror på modellen och tillförlitligheten hos inmatningen av data.

Tidslinje

1452–1519 gjorde Leonardo da Vinci många bidrag
1638: Galileo Galilei publicerade boken " Två nya vetenskaper " där han undersökte misslyckandet med enkla strukturer
1660: Hookes lag av Robert Hooke
1687: Isaac Newton publicerade " Philosophiae Naturalis Principia Mathematica " som innehåller Newtons rörelselagar
1750: Euler–Bernoullis strålekvation
1700–1782: Daniel Bernoulli introducerade principen om virtuellt arbete
1707–1783: Leonhard Euler utvecklade teorin om buckling av kolonner
1826: Claude-Louis Navier publicerade en avhandling om strukturers elastiska beteenden
1873: Carlo Alberto Castigliano presenterade sin avhandling " Intorno ai sistemi elastici ", som innehåller hans teorem för beräkning av förskjutning som partiell derivata av töjningsenergin. Denna sats inkluderar metoden "minst arbete" som ett specialfall
1878-1972 Stephen Timosjenko far till modern tillämpad mekanik inklusive Timoshenko-Ehrenfest strålteorin
1936: Hardy Cross publicerar momentfördelningsmetoden som senare erkändes som en form av relaxationsmetoden tillämpbar på problemet med flöde i rörnät
1941: Alexander Hrennikoff lämnade in sin D.Sc. avhandling i MIT om diskretisering av planelasticitetsproblem med hjälp av ett gitterramverk
1942: R. Courant delade upp en domän i ändliga underregioner
1956: J. Turner, RW Clough , HC Martin och LJ Topps artikel om "Stiffness and Deflection of Complex Structures" introducerar namnet "finite-element method" och är allmänt erkänd som den första heltäckande behandlingen av metoden som den är. känt idag

Se även