Optimering av diskontinuitetslayout

Felmekanism för en inbäddad grund (identifierad med DLO)

Discontinuity layout optimization (DLO) är en teknisk analysprocedur som kan användas för att direkt fastställa mängden last som kan bäras av ett fast material eller struktur innan kollaps. Genom att använda DLO identifieras layouten av felplan, eller "diskontinuiteter", i ett kollapsande material eller struktur med hjälp av matematiska optimeringsmetoder (därav namnet "diskontinuitetslayoutoptimering"). Det antas att fel uppstår på ett duktilt eller " plastiskt " sätt.

Hur det fungerar

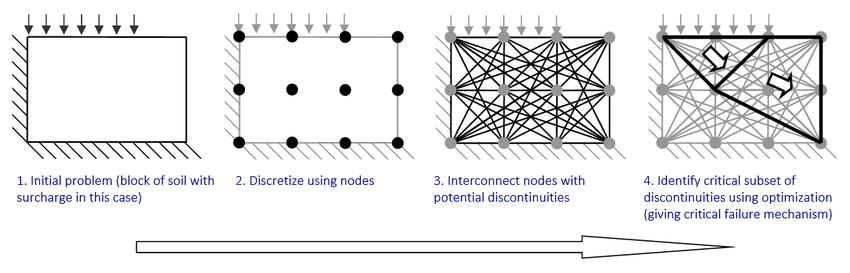
DLO-proceduren innefattar ett antal steg, som beskrivs nedan.

Explains steps involved when analysing a solid body using discontinuity layout optimization (DLO)

Uppsättningen av potentiella diskontinuiteter kan inkludera diskontinuiteter som korsar varandra, vilket gör att komplexa felmönster kan identifieras (t.ex. involverande "fläkt"-mekanismer, där många diskontinuiteter strålar ut från en punkt).

DLO kan formuleras i termer av jämviktsrelationer ('statisk' formulering) eller i termer av förskjutningar ('kinematisk' formulering). I det senare fallet är syftet med det matematiska optimeringsproblemet att minimera den inre energin som försvinner längs diskontinuiteter, med förbehåll för nodkompatibilitetsbegränsningar. Detta kan lösas med hjälp av effektiva linjära programmeringstekniker och, i kombination med en algoritm som ursprungligen utvecklades för problem med trusslayoutoptimering, har det visat sig att modern datorkraft kan användas för att direkt söka igenom ett mycket stort antal olika felmekanismtopologier (upp till ca 2 1 000 000 000 olika topologier på nuvarande generations datorer). En fullständig beskrivning av tillämpningen av DLO på plan töjningsproblem har tillhandahållits av Smith och Gilbert, till murverksbågsanalys av Gilbert et al, på plattproblem av Gilbert et al, och på 3D-problem av Hawksbee et al, och Zhang.

DLO vs FEM

Medan med finita elementanalys (FEM), en allmänt använd alternativ ingenjörsanalysprocedur , bildas matematiska relationer för det underliggande kontinuummekanikproblemet , innebär DLO analys av ett potentiellt mycket enklare diskontinuumproblem, där problemet helt och hållet ställs i termer av individen. diskontinuiteter som sammanbinder noder som är utlagda över kroppen under övervägande. När finita elementprogram för allmänna ändamål används för att analysera kollapstillståndet krävs dessutom ofta relativt komplexa icke-linjära lösare, i motsats till de enklare linjära programmeringslösare som vanligtvis krävs i fallet med DLO.

Jämfört med icke-linjär FEM har DLO följande fördelar och nackdelar:

Fördelar

  • Kollapstillståndet analyseras direkt, utan att behöva iterera. Det gör att lösningar generellt kan fås mycket snabbare.
  • Resultatet, i form av animerade felmekanismer, är i allmänhet lättare att tolka.
  • Problem som involverar singulariteter i spännings- eller förskjutningsfälten kan hanteras utan svårighet.
  • Eftersom DLO är mycket enklare än icke-linjär FEM kräver användare mindre träning för att kunna använda metoden effektivt.

Nackdelar

  • Som med andra gränsanalystekniker , tillhandahåller DLO ingen information om förskjutningar (eller spänningar) före kollaps.
  • DLO är i grunden baserad på modellering av kompatibla mekanismer för jordkollaps och är därför en övre gräns metod . Som ett resultat kommer metoden alltid att förutsäga en okonservativ kollapsbelastning.
  • Även om diskontinuitetslayoutgenereringen och linjära programmeringsoptimeringsscheman som används i DLO vanligtvis säkerställer att en bra approximation av den verkliga kollapsmekanismen hittas, finns det inget sätt att urskilja hur mycket den förutsagda kollapsbelastningen kommer att överstiga den verkliga kollapsbelastningen utan jämförelse med en oberoende nedre gränsanalys .
  • DLO är en relativt ny teknik så endast ett begränsat utbud av mjukvaruverktyg är för närvarande tillgängliga.

Ansökningar

DLO är kanske mest användbart för tekniska problem där traditionella handberäkningar är svåra, eller förenklar problemet för mycket, men där det inte är motiverat att använda mer komplexa icke-linjära FEM. Applikationer inkluderar:

Programvara som använder diskontinuitetslayoutoptimering

externa länkar

Hämtad från " https://en.wikipedia.org/w/index.php?title=Discontinuity_layout_optimization&oldid=1058711719 "