Stympad rhombicosidodecahedron

Stympad rhombicosidodecahedron
Schläfli symbol	trr{5,3} = $tr{\begin{Bmatrix}5\\3\end{Bmatrix}}$
Conway notation	taD = dålig
Ansikten	122: 60 {4} 20 {6} 30 {8} 12 {10}
Kanter	360
Vertices	240
Symmetrigrupp	I h , [5,3], (*532) order 120
Rotationsgrupp	I, [5,3] + , (532), ordning 60
Dubbel polyeder	Disdyakis hexecontahedron
Egenskaper	konvex

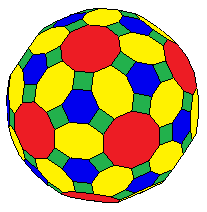
Inom geometrin är den trunkerade rhombicosidodecahedron en polyhedron , konstruerad som en trunkerad rhombicosidodecahedron . Den har 122 ytor: 12 dekagoner, 30 oktagoner, 20 hexagoner och 60 rutor.

Andra namn

• Stympad liten rhombicosidodecahedron
• Fasad icosidodecahedron

Zonohedron

Som en zonohedron kan den konstrueras med alla utom 30 oktagoner som vanliga polygoner . Den är 2-uniform, med 2 uppsättningar av 120 hörn som finns på två avstånd från dess centrum.

Denna polyeder representerar Minkowski summan av en trunkerad icosidodecahedron och en rombisk triacontahedron .

Besläktade polyedrar

Den stympade icosidodecahedron är liknande, med alla regelbundna ansikten, och 4.6.10 vertex figur . Se även den stympade rhombirhombicosidodecahedronen .

stympad icosidodecahedron	Stympad rhombicosidodecahedron
4.6.10	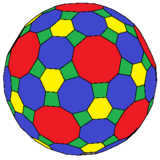4.8.10 och 4.6.8

Den trunkerade rhombicosidodecahedronen kan ses i sekvens av rättelse- och trunkeringsoperationer från icosidodecahedron . Ett ytterligare alterneringssteg leder till den snubbade rhombicosidodecahedronen .

namn	Icosidodecahedron _	Romb- icosidodeca- hedron	Stympad rhombicosidodecahedron _	Snub romb- icosidodecahedron
Coxeter	ID (rD)	rID (rrD)	trID (trrD)	srID (htrrD)
Conway	aD	aaD = eD	taaD = dålig	ledsen
Bild
Conway	jD	oD	galen	gaD
Dubbel

Se även

• Expanderad icosidodecahedron
• Stympad rhombicuboctahedron

• Eppstein, David (1996). "Zonoedrar och zonotoper" . Mathematica in Education and Research . 5 (4): 15–21.
•   Coxeter Regular Polytopes , tredje upplagan, (1973), Dover upplagan, ISBN 0-486-61480-8 (s. 145–154 Kapitel 8: Trunkering)
•   John H. Conway , Heidi Burgiel, Chaim Goodman-Strauss , The Symmetries of Things 2008, ISBN 978-1-56881-220-5

externa länkar

• George Harts Conway-tolkare : genererar polyedrar i VRML och tar Conway-notation som indata