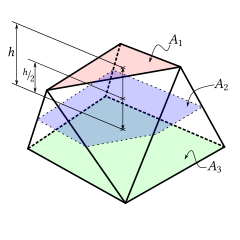
Prismatoid

Prismatoid med parallella ytor A ₁ och A ₃ , halvvägs tvärsnitt A ₂ och höjd h

Inom geometrin är en prismatoid en polyeder vars hörn alla ligger i två parallella plan . Dess sidoytor kan vara trapetser eller trianglar . Om båda planen har samma antal hörn, och sidoytorna är antingen parallellogram eller trapezoider, kallas det en prismoid .

Volym

Om områdena för de två parallella ytorna är A ₁ och A ₃ , är tvärsnittsarean för skärningen av prismatoiden med ett plan mitt emellan de två parallella ytorna A ₂ , och höjden (avståndet mellan de två parallella ytorna ) är h , då ges volymen av prismatoiden av $V={\frac {h(A_{1}+4A_{2}+A_ {3})}{6}}$ (Denna formel följer omedelbart genom att integrera arean parallellt med de två hörnsplanen med Simpsons regel , eftersom den regeln är exakt för integration av polynom med grader upp till 3, och i detta fall arean är högst en kvadratisk funktion i höjden.)

Prismatoida familjer

Pyramider	Kilar	Parallelepipeds	Prismor	Antiprismor			Kupoler	Frusta

Familjer av prismatoider inkluderar:

• Pyramider , där ett plan bara innehåller en enda punkt;
• Kilar , där ett plan endast innehåller två punkter;
• Prismor , vars polygoner i varje plan är kongruenta och förenade med rektanglar eller parallellogram;
• Antiprismor , vars polygoner i varje plan är kongruenta och sammanfogade av en omväxlande remsa av trianglar;
• Stjärnantiprismor ;
• Kupoler , där polygonen i det ena planet innehåller dubbelt så många punkter som det andra och är förenad med den genom omväxlande trianglar och rektanglar;
• Frusta erhållen genom trunkering av en pyramid;
• Fyrkantiga hexaedriska prismatoider :
  1. Parallelepipeds – sex parallellogramytor
  2. Romboeder – sex rombeansikten
  3. Trigonala trapezoeder – sex kongruenta rombeansikten
  4. Kuboider – sex rektangulära ytor
  5. Fyrkantig frusta – en spets – stympad fyrkantig pyramid
  6. Kub – sex fyrkantiga ytor

Högre dimensioner

En tetraedrisk-kuboktaedrisk kupol.

I allmänhet är en polytop prismatoidal om dess hörn finns i två hyperplan . Till exempel, i fyra dimensioner, kan två polyedrar placeras i två parallella 3-utrymmen och förbindas med polyedriska sidor.

externa länkar

• Weisstein, Eric W. "Prismatoid" . MathWorld .