Komma (musik)

I musikteori är kommatecken ett mycket litet intervall , skillnaden beror på att man stämmer en ton på två olika sätt. Strängt taget finns det bara två sorters kommatecken, det syntoniska kommatecken , "skillnaden mellan en bara stor 3:e och en fyra precis perfekta 5:e minus två oktaver", och det pytagoreiska kommatecken , "skillnaden mellan tolv 5:e och sju oktaver". Ordet kommatecken som används utan förbehåll hänvisar till det syntoniska kommatecken , som till exempel kan definieras som skillnaden mellan en F ♯ avstämd med det D-baserade pytagoreiska avstämningssystemet , och en annan F ♯ avstämd med det D-baserade kvartskomma meantone tuning system . Intervaller separerade av förhållandet 81:80 anses vara samma ton eftersom den västerländska kromatiska skalan med 12 toner inte skiljer Pythagoras intervall från 5-gränsintervall i sin notation. Andra intervall anses kommatecken på grund av de enharmoniska ekvivalenserna hos ett avstämningssystem. Till exempel, i 53TET är B ♭ och A ♯ båda approximerade med samma intervall även om de är en septimal kleisma från varandra.

Ordet "komma" kom via latin från grekiska κόμμα, från tidigare *κοπ-μα = "en handling att skära".

Inom samma stämningssystem kan två enharmoniskt ekvivalenta toner (som G ♯ och A ♭ ) ha en något annorlunda frekvens, och intervallet mellan dem är ett kommatecken. Till exempel, i utökade skalor som produceras med fem-limit-stämning är en A ♭ stämd som en durterts under C ₅ och en G ♯ stämd som två dur-tertsar över C ₄ inte exakt samma ton, eftersom de skulle ha samma temperament . Intervallet mellan dessa toner, diesis , är ett lätt hörbart kommatecken (dess storlek är mer än 40 % av en halvton ).

Komma definieras ofta som skillnaden i storlek mellan två halvtoner. ^{[ citat behövs ]} Varje stämningssystem för medeltonstemperament producerar en 12-tonsskala som kännetecknas av två olika sorters halvtoner (diatoniska och kromatiska), och därmed av ett kommatecken av unik storlek. Detsamma gäller för Pythagoras stämning.

Mindre diesis definieras i kvarts-komma-medelton som skillnad mellan halvtoner ( m2 − A1 ), eller intervall mellan enharmoniskt ekvivalenta toner (från C ♯ till D ♭ ). Intervallet från C till D är snävare än i Pythagoras stämning (se nedan).

Pythagoras kommatecken (PC) definieras i Pythagoras stämning som skillnad mellan halvtoner ( A1 − m2 ), eller intervall mellan enharmoniskt ekvivalenta toner (från D ♭ till C ♯ ). Intervallet från C till D är bredare än i kvartskomma-medelton (se ovan).

Med bara intonation kan mer än två typer av halvtoner produceras. Således kan ett enda avstämningssystem kännetecknas av flera olika kommatecken. Till exempel producerar en vanlig version av fem-gräns-stämning en 12-tonsskala med fyra sorters halvtoner och fyra kommatecken .

Storleken på kommatecken uttrycks vanligtvis och jämförs i termer av cent – 1 ⁄ 1200 bråkdelar av en oktav på en logaritmisk skala.

Komma i olika sammanhang

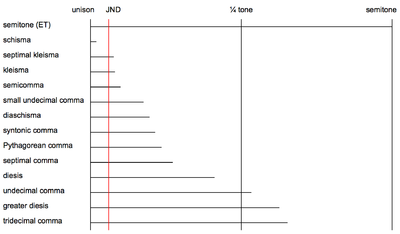
Jämförelse av storleken på olika kommatecken, i cent. Lika tempererad halvton tillagd för jämförelse. JND är den precis märkbara skillnaden mellan toner.

I kolumnen nedan märkt "Skillnad mellan halvtoner " är m2 den mindre sekunden (diatonisk halvton), A1 är den förstärkta unisonen (kromatisk halvton), och S ₁ , S ₂ , S ₃ , S ₄ är halvtoner enligt definitionen här . I kolumnerna märkta " Intervall 1" och "Intervall 2" antas alla intervaller vara inställda med enbart intonation . Lägg märke till att det pytagoreiska kommatecken ( PC ) och det syntoniska kommatecken ( SC ) är grundläggande intervall som kan användas som måttstockar för att definiera några av de andra kommatecken. Till exempel är skillnaden mellan dem ett litet kommatecken som kallas schisma . En schisma är inte hörbar i många sammanhang, eftersom dess storlek är smalare än den minsta hörbara skillnaden mellan toner (som är runt sex cent, även känd som just-noticeable difference , eller JND).

Namn på kommatecken	Alternativt namn	Definitioner				Storlek
		Skillnad mellan halvtoner	Skillnad mellan kommatecken	Skillnad mellan		Cents	Förhållande
		Skillnad mellan halvtoner	Skillnad mellan kommatecken	Intervall 1	Intervall 2	Cents	Förhållande
Schisma	Skhisma	A1 − m2 i 1 ⁄ 12 -komma- medelton	1 PC − 1 SC	8 perfekta kvintar + 1 majortrea	5 oktaver	1,95	32805:32768
Septimal kleisma				3 stora tredjedelar	1 oktav − 1 septimal kommatecken	7,71	225:224
Kleisma				6 mindre tredjedelar	Tritav (1 oktav + 1 perfekt femtedel )	8.11	15625:15552
Litet undecimalt kommatecken				1 neutral sekund	1 Mindre ton	17.40	100:99
Diaschisma	Diaskhisma	m2 − A1 i 1 ⁄ 6 -komma-medelton, S ₃ − S ₂ i 5-gränsinställning	2 SC − 1 st	3 oktaver	4 perfekta kvintar + 2 stora tertsar	19.55	2048:2025
Syntoniskt kommatecken (SC)	Didymus kommatecken	S ₂ − S ₁ i 5-limit tuning		4 perfekta femmor	2 oktaver + 1 dur terts	21.51	81:80
Syntoniskt kommatecken (SC)	Didymus kommatecken	S ₂ − S ₁ i 5-limit tuning		Stor ton	Mindre ton	21.51	81:80
Pythagoras kommatecken (PC)	Ditoniskt kommatecken	A1 − m2 i Pythagoras stämning		12 perfekta femmor	7 oktaver	23.46	531441:524288
Septimalt kommatecken	Archytas kommatecken			Mindre sjua	Septimal moll sjunde	27.26	64:63
Diesis	Mindre diesis minskade andra	m2 − A1 i 1 ⁄ 4 -komma-medelton , S ₃ − S ₁ i 5-gränsinställning	3 SC − 1 st	Oktav	3 stora tredjedelar	41,06	128:125
Odecimalt kommatecken	Odecimal kvartston			Undecimal tritonus	Perfekt fjärde	53,27	33:32
Större diesis		m2 − A1 i 1⁄ 3 -komma -medelton, S ₄ − S ₁ i 5-limit-inställning	4 SC − 1 st	4 mindre tredjedelar	Oktav	62,57	648:625
Tridecimalt kommatecken	Tredecimal tredje ton			Tridecimal triton	Perfekt fjärde	65,34	27:26

Många andra kommatecken har räknats upp och namngivits av mikrotonalister.

Det syntoniska kommatecken har en avgörande roll i musikhistorien. Det är den mängd med vilken några av tonerna som producerats i Pythagoras stämning tillplattades eller vässades för att producera bara små och stora tertsar. I Pythagoras stämning var de enda högkonsonanta intervallen den perfekta femman och dess inversion, den perfekta fjärden . Pythagoras dur terts (81:64) och moll terts (32:27) var dissonanta , och detta hindrade musiker från att fritt använda treklanger och ackord , vilket tvingade dem att skriva musik med relativt enkel textur . Under senmedeltiden insåg musiker att genom att lätt dämpa tonhöjden på vissa toner kunde de pytagoreiska tertsarna göras konsonanta . Till exempel, om du minskar med ett syntoniskt kommatecken (81:80) blir frekvensen för E, C–E (en stor terts) och E–G (en mindre tredjedel) bara: C–E plattas ut till ett rättvist intonerat förhållande av

{\frac {81}{64}}\cdot {\frac {80}{81}}={\frac {1\cdot 5} {4\cdot 1}}={\frac {5}{4}}

och samtidigt skärps E–G till det justa förhållandet mellan

{\frac {32}{27}}\cdot {\frac {81}{80}}={\frac {2\cdot 3} {1\cdot 5}}={\frac {6}{5}}

Detta ledde till skapandet av ett nytt stämningssystem , känt som quarter-comma meantone , som tillät den fulla utvecklingen av musik med komplex textur , såsom polyfonisk musik , eller melodier med instrumentalt ackompanjemang . Sedan dess har andra stämningssystem utvecklats, och det syntoniska kommatecken användes som referensvärde för att temperera de perfekta kvintarna genom hela familjen av syntoniska temperament , inklusive medeltonstemperament .

Alternativa definitioner

I kvartskomma meantone , och alla typer av meantone temperament tuning system som tempererar femman till en storlek mindre än 700 cent, är kommatecken en förminskad sekund , vilket kan definieras på samma sätt som skillnaden mellan:

moll sekund och förstärkt unison (även känd som diatoniska och kromatiska halvtoner ), eller
dur tvåa och förminskad trea , eller
mindre tredje och förstärkt tvåa , eller
dur tredje och minskad fjärde , eller
perfekt fjärde och utökad tredje , eller
utökad fjärde och minskad femma , eller
perfekt femma och minskad sexa , eller
mindre sjätte och förstärkt femma , eller
dur sjätte och förminskad sjua , eller
moll sjunde och utökad sjätte , eller
dur sjunde och förminskad oktav .

I Pythagoras stämning, och alla slags medeltonstemperamentstämningssystem som tempererar femman till en storlek större än 700 cent (t.ex. 1 ⁄ 12 -kommamedelton), är kommatecken motsatsen till en minskad sekund, och därför motsatsen till ovannämnda skillnader. Mer exakt, i dessa avstämningssystem är den minskade sekunden ett fallande intervall, medan kommatecken är dess stigande motsats. Till exempel kan det pytagoreiska kommatecken (531441:524288, eller cirka 23,5 cent) beräknas som skillnaden mellan en kromatisk och en diatonisk halvton, vilket är motsatsen till en pytagoreisk förminskad sekund (524288:531441 cents) eller 5 cirka cents. .

I vart och ett av de ovan nämnda avstämningssystemen har de ovan angivna skillnaderna alla samma storlek. Till exempel, i pythagoras stämning är de alla lika med motsatsen till ett pythagoras kommatecken , och i kvartskomma meanton är de alla lika med en diesis .

Notation

Under åren 2000–2004 arbetade Marc Sabat och Wolfgang von Schweinitz tillsammans i Berlin för att utveckla en metod för att exakt ange tonhöjder i notanteckningar. Denna metod kallades den utökade Helmholtz-Ellis JI tonhöjdsnotationen. Sabat och Schweinitz tar de "konventionella" flats, naturals och sharps som en Pythagoras serie av perfekta femmor. En serie av perfekta kvintdelar som börjar med F fortsätter alltså CGDAEBF ♯ och så vidare. Fördelen för musiker är att konventionell läsning av de grundläggande fjärderna och femmorna förblir bekant. Ett sådant tillvägagångssätt har också förespråkats av Daniel James Wolf och av Joe Monzo, som refererar till det med akronymen HEWM (Helmholtz-Ellis-Wolf-Monzo). I Sabat-Schweinitz-designen markeras syntoniska kommatecken med pilar fästa på det platta, naturliga eller skarpa tecknet, septimala kommatecken med Giuseppe Tartinis symbol och undecimala kvarttoner med vanliga kvarttonstecken (ett enda kors och baklänges platt ) . För högre primtal har ytterligare skyltar designats. För att underlätta snabb uppskattning av tonhöjder kan centindikationer läggas till (nedåtgående avvikelser under och uppåtgående avvikelser över respektive oavsiktlig). Konventionen som används är att de skrivna centen refererar till den härdade tonhöjden som antyds av det platta, naturliga eller skarpa tecknet och notens namn. En av de stora fördelarna med en sådan notation är att den gör att den naturliga övertonsserien kan noteras exakt. En fullständig förklaring och teckensnitt för notationen (se exempel) är öppen källkod och tillgängliga från Plainsound Music Edition. ^{[ fullständig hänvisning behövs ]} Således är en pytagoreisk skala CDEFGABC , medan en rättvis skala är CDE FGA B C.

Kompositören Ben Johnston använder ett "−" som en tillfällighet för att indikera att en ton sänks ett syntoniskt kommatecken, eller ett "+" för att indikera att en ton höjs ett syntoniskt kommatecken; Johnstons "grundskala" (de vanliga nominalen ABCDEFG ) är dock inställd på just-intonation och inkluderar alltså redan det syntoniska kommatecken. Således är en pytagoreisk skala CD E+ FG A+ B+ C , medan en rättvis skala är CDEFGAB .

Tempering av kommatecken

Komma används ofta i beskrivningen av musikaliska temperament , där de beskriver skillnader mellan musikaliska intervaller som elimineras av det stämningssystemet. Ett kommatecken kan ses som avståndet mellan två musikaliska intervall. När ett visst kommatecken dämpas i ett avstämningssystem, elimineras möjligheten att skilja mellan dessa två intervaller i den inställningen. Till exempel, skillnaden mellan den diatoniska halvtonen och den kromatiska halvtonen kallas diesis. Det flitigt använda 12-tons lika temperamentet tempererar ut diesisen och skiljer därmed inte mellan de två olika typerna av halvtoner. Å andra sidan dämpar 19-tons lika temperament inte detta kommatecken, och därför skiljer det mellan de två halvtonerna.

Exempel:

12-TET dämpar diesis, såväl som en mängd andra kommatecken.
19-TET tempererar septimal diesis och syntoniska kommatecken , men tempererar inte diesisen.
22-TET tempererar septimala kommatecken från Archytas , men tempererar inte septimal diesis eller syntonisk komma.
31-TET tempererar det syntoniska kommatecken, såväl som kommat som definieras av förhållandet (99:98), men tempererar inte diesis, septimal diesis eller septimala komma för Archytas.

Följande tabell listar antalet använda steg som motsvarar olika just-intervaller i olika avstämningssystem. Nollor indikerar att intervallet är ett kommatecken (dvs. är uthärdat) i just det lika temperamentet.

Intervall	5-TEDO	7-TEDO	12-TEDO	19-TEDO	22-TEDO	31-TEDO	34-TEDO	41-TEDO	53-TEDO	72-TEDO
2/1	5	7	12	19	22	31	34	41	53	72
15/8	5	6	11	17	20	28	31	37	48	65
9/5	4	6	10	16	19	26	29	35	45	61
7/4	4	6	10	15	18	25	28	33	43	58
5/3	4	5	9	14	16	23	25	30	39	53
8/5	3	5	8	13	15	21	23	28	36	49
3/2	3	4	7	11	13	18	20	24	31	42
10/7	3	3	6	10	11	16	17	21	27	37
64/45	2	4	6	10	11	16	17	21	27	37
45/32	3	3	6	9	11	15	17	20	26	35
7/5	2	4	6	9	11	15	17	20	26	35
4/3	2	3	5	8	9	13	14	17	22	30
9/7	2	2	4	7	8	11	12	15	19	26
5/4	2	2	4	6	7	10	11	13	17	23
6/5	1	2	3	5	6	8	9	11	14	19
7/6	1	2	3	4	5	7	8	9	12	16
8/7	1	1	2	4	4	6	6	8	10	14
9/8	1	1	2	3	4	5	6	7	9	12
10/9	1	1	2	3	3	5	5	6	8	11
27/25	0	1	1	2	3	3	4	5	6	8
15/14	1	0	1	2	2	3	3	4	5	7
16/15	0	1	1	2	2	3	3	4	5	7
21/20	0	1	1	1	2	2	3	3	4	5
25/24	1	0	1	1	1	2	2	2	3	4
648/625	-1	1	0	1	2	1	2	3	3	4
28/27	0	1	1	1	1	2	2	2	3	4
36/35	0	0	0	1	1	1	1	2	2	3
128/125	-1	1	0	1	1	1	1	2	2	3
49/48	0	1	1	0	1	1	2	1	2	2
50/49	1	-1	0	1	0	1	0	1	1	2
64/63	0	0	0	1	0	1	0	1	1	2
531441/524288	1	-1	0	-1	2	-1	2	1	1	0
81/80	0	0	0	0	1	0	1	1	1	1
2048/2025	-1	1	0	1	0	1	0	1	1	2
126/125	-1	1	0	0	1	0	1	1	1	1
1728/1715	0	-1	-1	1	0	0	-1	1	0	1
2109375/2097152	3	-2	1	-1	0	0	1	-1	0	-1
15625/15552	2	-1	1	0	-1	1	0	-1	0	0
225/224	1	-1	0	0	0	0	0	0	0	0
32805/32768	1	-1	0	-1	1	-1	1	0	0	-1
2401/2400	-1	2	1	-1	1	0	2	0	1	0
4375/4374	-1	0	-1	0	1	-1	0	1	0	0

Kommat kan också betraktas som det intervall som återstår efter en hel cirkel av intervall. Pythagoras kommatecken, till exempel, är skillnaden som erhålls, säg, mellan A ♭ och G ♯ efter en cirkel på tolv bara femtedelar. En cirkel med tre bara stora tredjedelar, såsom A ♭ –C–E–G ♯ , producerar den lilla diesis 125/128 (41,1 cent) mellan G ♯ och A ♭ . En cirkel med fyra mindre tredjedelar, som G ♯ –B–D–F–A ♭ , ger ett intervall på 648/625 mellan A ♭ och G ♯ . Etc. En intressant egenskap hos temperament är att denna skillnad förblir oavsett inställningen av intervallen som bildar cirkeln. I denna mening kan kommatecken och andra minutintervall aldrig dämpas helt, oavsett inställning.

Kommasekvens

En kommasekvens definierar ett musikaliskt temperament genom en unik sekvens av kommatecken vid ökande primtalsgränser . Det första kommatecken i kommasekvensen är i q-gränsen, där q är det n:te udda primtal och n är antalet generatorer . Efterföljande kommatecken är i primtalsgränser, vart och ett primtal bortom det sista.

Andra intervall som kallas kommatecken

Det finns också flera intervall som kallas kommatecken, som tekniskt sett inte är kommatecken eftersom de inte är rationella bråk som de ovan, utan är irrationella approximationer av dem. Dessa inkluderar Holdrian och Mercators kommatecken.

Se även