12 lika temperament

12-tons lika temperament kromatisk skala på C, en hel oktav stigande, noterad endast med skarpa toner.   Spela stigande och fallande

Tolvtons lika temperament (12-TET) är det musiksystem som delar upp oktaven i 12 delar, som alla är lika tempererade (lika fördelade) på en logaritmisk skala , med ett förhållande lika med den 12:e roten av 2 ( ¹² √ 2 ≈ 1,05946). Det resulterande minsta intervallet, 1 ⁄ 12 av en oktavs bredd, kallas ett halvtons- eller halvsteg.

Tolvtoners lika temperament är det mest utbredda systemet inom musik idag. Det har varit det dominerande stämningssystemet för västerländsk musik, från och med klassisk musik , sedan 1700-talet, och Europa använde nästan uteslutande approximationer av det i årtusenden innan dess. Det har också använts i andra kulturer.

I modern tid är 12-TET vanligtvis stämt i förhållande till en standardtonhöjd på 440 Hz, kallad A440 , vilket betyder att en ton, A , är stämd till 440 hertz och alla andra toner definieras som en multipel av halvtoner förutom den, antingen högre eller lägre i frekvens . Standardtonen har inte alltid varit 440 Hz. Den har varierat och generellt stigit under de senaste hundra åren.

Historia

De två figurer som ofta krediteras för att ha uppnått exakt beräkning av tolvtoners lika temperament är Zhu Zaiyu (även romaniserad som Chu-Tsaiyu. Kinesiska: 朱載堉 ) 1584 och Simon Stevin 1585. Enligt Fritz A. Kuttner, en kritiker av teorin, är det känt att "Chu-Tsaiyu presenterade en mycket exakt, enkel och genialisk metod för aritmetisk beräkning av lika temperament mono-ackord 1584" och att "Simon Stevin erbjöd en matematisk definition av lika temperament plus en något mindre exakt beräkning av motsvarande numeriska värden 1585 eller senare." Utvecklingen skedde oberoende av varandra.

Kenneth Robinson tillskriver uppfinningen av lika temperament till Zhu Zaiyu och ger textcitat som bevis. Zhu Zaiyu citeras för att ha sagt att i en text från 1584: "Jag har grundat ett nytt system. Jag fastställer en fot som det nummer från vilket de andra ska extraheras, och med hjälp av proportioner extraherar jag dem. Sammantaget måste man hitta de exakta siffrorna för pitch-pipers i tolv operationer." Kuttner håller inte med och påpekar att hans påstående "inte kan anses vara korrekt utan större kvalifikationer." Kuttner föreslår att varken Zhu Zaiyu eller Simon Stevin uppnådde samma temperament och att ingen av de två ska behandlas som uppfinnare.

Kina

Tidig historia

En komplett uppsättning bronsklockor, bland många musikinstrument som finns i graven till markisen Yi av Zeng (tidiga krigförande stater, ca 500-talet f.Kr. i den kinesiska bronsåldern), täcker fem hela 7-toners oktaver i tonarten av C-dur, inklusive 12 toner halvtoner i mitten av intervallet.

En approximation för lika temperament beskrevs av He Chengtian , en matematiker från södra och nordliga dynastier som levde från 370 till 447. Han kom ut med den tidigaste registrerade ungefärliga numeriska sekvensen i förhållande till lika temperament i historien: 900 849 802 . 715 677 638 601 570 536 509,5 479 450.

Zhu Zaiyu

Prince Zhu Zaiyu konstruerade 12 strängars lika temperament stämningsinstrument, framifrån och bakifrån

Zhu Zaiyu ( 朱載堉 ), en prins av Ming -hovet, tillbringade trettio år på forskning baserad på idén om lika temperament som ursprungligen postulerades av hans far. Han beskrev sin nya tonhöjdsteori i sin Fusion of Music and Calendar 律暦融通 som publicerades 1580. Detta följdes av publiceringen av en detaljerad redogörelse för den nya teorin om lika temperament med en exakt numerisk specifikation för 12-TET i hans 5 000 -sida arbete Komplett kompendium av musik och tonhöjd ( Yuelü quan shu 樂律全書 ) 1584. En utökad redogörelse ges också av Joseph Needham. Zhu erhöll sitt resultat matematiskt genom att successivt dividera längden på sträng och pipa med ¹² √ 2 ≈ 1,059463 och för rörlängd med ²⁴ √ 2 , så att efter tolv divisioner (en oktav) dividerades längden med en faktor 2:

$\left({\sqrt[{12}]{2}}\right)^{12}=2$

På liknande sätt, efter 84 divisioner (7 oktaver) dividerades längden med en faktor på 128:

$\left({\sqrt[{12}]{2}}\right)^{84}=2^{7}=128$

Zhu Zaiyu har krediterats som den första personen att lösa problemet med lika temperament matematiskt. Åtminstone en forskare har föreslagit att Matteo Ricci , en jesuit i Kina, spelade in detta arbete i sin personliga dagbok och kan ha överfört verket tillbaka till Europa. (Standardresurser på ämnet nämner inte någon sådan överföring.) År 1620 refererades Zhus arbete av en europeisk matematiker [ . Murray Barbour sa: "Det första kända utseendet på tryck av de korrekta siffrorna för lika temperament var i Kina, där prins Tsaiyüs briljanta lösning förblir en gåta." Den tyske 1800-talsfysikern Hermann von Helmholtz skrev i On the Sensations of Tone att en kinesisk prins (se nedan) introducerade en skala på sju toner, och att uppdelningen av oktaven i tolv halvtoner upptäcktes i Kina.

Zhu Zaiyus lika temperament pitch pipes

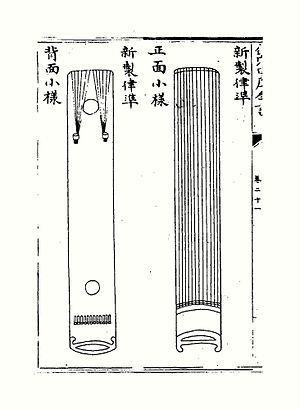
Zhu Zaiyu illustrerade sin teori om lika temperament genom konstruktionen av en uppsättning av 36 stämmor av bambu som sträcker sig i 3 oktaver, med instruktioner om typen av bambu, färg på färg och detaljerade specifikationer om deras längd och inre och yttre diametrar. Han konstruerade också ett 12-strängs stäminstrument, med en uppsättning stämningspipor gömda inuti dess nedre hålighet. 1890 duplicerade Victor-Charles Mahillon , intendent för Conservatoire-museet i Bryssel, en uppsättning pitchpipor enligt Zhu Zaiyus specifikation. Han sa att den kinesiska teorin om toner visste mer om längden på tonhöjdsrör än dess västerländska motsvarighet, och att uppsättningen av rör duplicerade enligt Zaiyu-data bevisade noggrannheten i denna teori.

Europa

Simon Stevins Van de Spiegheling der singconst c. 1605.

Tidig historia

En av de tidigaste diskussionerna om lika temperament förekommer i skriften av Aristoxenus på 300-talet f.Kr.

Vincenzo Galilei (fader till Galileo Galilei ) var en av de första praktiska förespråkarna för tolvtons lika temperament. Han komponerade en uppsättning danssviter på var och en av de 12 tonerna i den kromatiska skalan i alla "transpositionsnycklar", och publicerade också, i sin " Fronimo " från 1584, 24 + 1 ricercars . Han använde förhållandet 18:17 för att fretta lutan (även om viss justering var nödvändig för rena oktaver).

Galileis landsman och kollega lutenist Giacomo Gorzanis hade skrivit musik baserad på lika temperament 1567. Gorzanis var inte den enda lutenisten som utforskade alla lägen eller tonarter: Francesco Spinacino skrev en "Recercare de tutti li Toni" ( Ricercar in all the Tones) redan tidigt. som 1507. På 1600-talet skrev lutenisten-kompositören John Wilson en uppsättning av 30 preludier inklusive 24 i alla dur/moll tonarter. Henricus Grammateus närmade sig lika temperament 1518. De första stämningsreglerna i lika temperament gavs av Giovani Maria Lanfranco i hans "Scintille de musica". Zarlino i sin polemik med Galilei motsatte sig till en början lika temperament men medgav det så småningom i förhållande till lutan i sin Sopplimenti musicali 1588.

Simon Stevin

Det första omnämnandet av lika temperament relaterat till den tolfte roten av två i väst dök upp i Simon Stevins manuskript Van De Spiegheling der singconst (ca 1605), publicerat postumt nästan tre århundraden senare 1884. Men på grund av otillräcklig noggrannhet av hans beräkning var många av ackordlängdsnumren han fick en eller två enheter från de korrekta värdena. Som ett resultat har frekvensförhållandena i Simon Stevins ackord inget enhetligt förhållande, utan ett förhållande per ton, vilket av Gene Cho hävdas som felaktigt.

Följande var Simon Stevins ackordlängd från Van de Spiegheling der singconst :

Tona	Ackord 10000 från Simon Stevin	Förhållande	Rättat ackord
halvton	9438	1,0595465	9438,7
helton	8909	1,0593781
och en halv ton	8404	1,0600904	8409
ditone	7936	1,0594758	7937
ditone och en halv	7491	1,0594046	7491,5
triton	7071	1,0593975	7071.1
triton och en halv	6674	1,0594845	6674,2
fyrton	6298	1,0597014	6299
fyrton och en halv	5944	1,0595558	5946
femton	5611	1,0593477	5612.3
femton och en halv	5296	1,0594788	5297.2
full ton		1,0592000

En generation senare presenterade den franske matematikern Marin Mersenne flera lika tempererade ackordlängder erhållna av Jean Beaugrand, Ismael Bouillaud och Jean Galle.

År 1630 publicerade Johann Faulhaber en 100-cents monochord-tabell, som innehöll flera fel på grund av hans användning av logaritmiska tabeller. Han förklarade inte hur han fick sina resultat.

Barocktiden

Från 1450 till omkring 1800 föredrog plockade instrumentspelare (lutenister och gitarrister) i allmänhet lika temperament, och Brossard-lutmanuskriptet som sammanställdes under den sista fjärdedelen av 1600-talet innehåller en serie av 18 preludier tillskrivna Bocquet skrivna i alla tonarter, inklusive den sista preludium, med titeln Prelude sur tous les tons , som enharmoniskt modulerar genom alla tonarter. Angelo Michele Bartolotti publicerade en serie passacaglior i alla tonarter, med anslutande enharmoniskt modulerande passager. Bland 1600-talets klaviaturkompositörer Girolamo Frescobaldi lika temperament. Vissa teoretiker, som Giuseppe Tartini , var emot antagandet av lika temperament; de ansåg att förnedrande av renheten i varje ackord försämrade musikens estetiska tilltal, även om Andreas Werckmeister eftertryckligen förespråkade lika temperament i sin postumt publicerade avhandling från 1707.

Tolvtons jämnt temperament tog fäste av en mängd olika anledningar. Det var en bekväm passform för den befintliga klaviaturdesignen och tillät total harmonisk frihet med bördan av måttlig orenhet i varje intervall, särskilt ofullkomliga konsonanser. Detta möjliggjorde ett större uttryck genom enharmonisk modulering , som blev oerhört viktig på 1700-talet i musik av kompositörer som Francesco Geminiani , Wilhelm Friedemann Bach , Carl Philipp Emmanuel Bach och Johann Gottfried Müthel . Tolvtons lika temperament hade vissa nackdelar, såsom imperfekta tredjedelar, men när Europa bytte till lika temperament, ändrade det musiken som det skrev för att passa systemet och minimera dissonans.

framåt beskrivs i detalj i en hel del moderna vetenskapliga publikationer: det var redan det temperament som valdes under den klassiska eran (andra hälften av 1700-talet), [ citat behövs det blev standard under den tidiga romantiska eran (första decenniet av 1800-talet), förutom organ som bytte till det mer gradvis, och slutförde först under det andra decenniet av 1800-talet. (I England höll några katedralorganister och körledare emot det även efter det datumet; Samuel Sebastian Wesley , till exempel, motsatte sig det hela tiden. Han dog 1876.)

Ett exakt lika temperament är möjligt genom att använda Sabbatini-metoden från 1600-talet för att dela upp oktaven först i tre tempererade stora tertsar. Detta föreslogs också av flera författare under den klassiska eran. Trimning utan slaghastigheter men med flera kontroller, för att uppnå praktiskt taget modern noggrannhet, gjordes redan under de första decennierna av 1800-talet. Att använda taktfrekvenser, som först föreslogs 1749, blev vanligt efter deras spridning av Helmholtz och Ellis under andra hälften av 1800-talet. Den ultimata precisionen var tillgänglig med tabeller med två decimaler publicerade av White 1917.

Det är i en miljö med lika temperament som de nya stilarna av symmetrisk tonalitet och polytonalitet , atonal musik som den skriven med tolvtonsteknik eller serialism och jazz (åtminstone dess pianokomponent) utvecklades och blomstrade.

Jämförelse av historiska approximationer av halvtonen

År	namn	Förhållande	Cents
400	Han Chengtian	1,060070671	101,0
1580	Vincenzo Galilei	18:17 [1.058823529]	99,0
1581	Zhu Zaiyu	1,059463094	100,0
1585	Simon Stevin	1,059546514	100,1
1630	Marin Mersenne	1,059322034	99,8
1630	Johann Faulhaber	1,059490385	100,0

Matematiska egenskaper

En oktav på 12-tet på ett monochord

I tolvtons lika temperament, som delar oktaven i 12 lika delar, är bredden på en halvton , dvs. frekvensförhållandet för intervallet mellan två intilliggande toner, den tolfte roten av två :

${\sqrt[{12}]{2}}=2^{\frac {1}{12}}\approx 1,059463$

Detta intervall är uppdelat i 100 cent .

Beräknar absoluta frekvenser

Se även: Piano tangentfrekvenser

För att hitta frekvensen, P _n , för en not i 12-TET kan följande definition användas:

$P_{n}=P_{a}\left({\sqrt[{12}]{2}}\right)^{(na)}$

I denna formel hänvisar P _n till tonhöjden, eller frekvensen (vanligtvis i hertz ), du försöker hitta. Pa _hänvisar till frekvensen för en referens tonhöjd. n och a hänvisar till nummer som tilldelats den önskade tonhöjden respektive referens tonhöjden. Dessa två tal är från en lista över på varandra följande heltal som tilldelats på varandra följande halvtoner. Till exempel är A ₄ (referens tonhöjden) den 49:e tangenten från den vänstra änden av ett piano (stämd till 440 Hz ), och C ₄ ( mitten C ), och F# ₄ är den 40:e respektive 46:e tangenten. Dessa siffror kan användas för att hitta frekvensen för C ₄ och F# ₄ :

$P_{40}=440\left({\sqrt[{12}]{2}}\right)^{(40-49 )}\approx 261.626\ \mathrm {Hz}$

$P_{46}=440\left({\sqrt[{12}] 2}}\right)^{(46-49)}\approx 369.994\ \mathrm {Hz}$

Bara intervaller

Intervallet för 12-TET är nära vissa intervaller i enbart intonation .

Efter gräns

12-TET är mycket exakt i 3-gränsen, men när man ökar primtalsgränserna till 11 blir det gradvis värre med ungefär en sjättedel av en halvton varje gång. Dess elfte och trettonde övertoner är extremt inexakta. 12-TET:s sjuttonde och nittonde övertoner är nästan lika exakta som dess tredje överton, men vid det här laget har primtalsgränsen blivit för hög för att låta konsonant för de flesta.

3-gräns

Se även: Pythagoras stämning

12-TET har en mycket bra approximation av den perfekta kvinten (3/2) och dess inversion , den perfekta fjärdedelen (4/3), speciellt för uppdelningen av oktaven i ett relativt litet antal toner. Närmare bestämt är en precis perfekt femte något mindre än två cent, vilket är en femtiondel av en halvton, skarpare än den lika tempererade approximationen. Eftersom durtonen (9/8) helt enkelt är två perfekta kvintar minus en oktav, och dess inversion, den pythagoreiska mollsjunden (16/9), helt enkelt är två perfekta fjärdedelar, behåller de för det mesta precisionen som deras föregångare; felet fördubblas, men det förblir litet – faktiskt så litet att människor inte kan uppfatta det. Man kan fortsätta att använda bråk med högre potens av tre, de nästa två är 27/16 och 32/27, men när termerna för bråken blir större blir de mindre tilltalande för örat.

5-gräns

Se även: Trimning med fem gränser

12-TET:s approximation av den femte övertonen (5/4) är mellan en sjätte och en sjundedel av en halvton av. Eftersom intervaller som är mindre än en fjärdedel av en skala avtrappas fortfarande låter i harmoni, har 12-TET en instämd femte överton som kan användas för att generera andra femgränsintervall, som 5/3 och 8/5, med lika stora fel. Västerländsk musik drar fördel av den instämda femte övertonen, till exempel genom att använda den i den aritmetiska sekvensen 4:5:6 .

7-gräns

Se även: 7-limit tuning

12-TET:s approximation av den sjunde övertonen (7/4) är ungefär en tredjedel av en halvton av. Eftersom felet är större än en kvarts halvton tenderar sju-gränsintervaller i 12-TET att låta ostämda. I tritonsbråken 7/5 och 10/7 tar felen i den femte och sjunde övertonen delvis ut varandra så att de rättvisa bråken är inom en kvarts halvton av deras lika-tempererade ekvivalenter, men tritonen låter fortfarande dissonant för de flesta.

11- och 13-gränser

Den elfte övertonen (11/8) är cirka 550 cent, vilket innebär att den faller nästan exakt mellan de närmaste två lika tempererade intervallen i 12-TET och därför inte approximeras av någondera. Faktum är att 11/8 är nästan så långt ifrån alla lika tempererade approximationer som möjligt i 12-TET. Den trettonde övertonen (13/8) är nästan lika inexakt. Detta betyder dock att bråket 13/11 (och även dess inversion, 22/13) är exakt approximerat med 12-TET (specifikt med tre halvtoner) eftersom felen i den elfte och trettonde övertonen tar ut varandra. De flesta är dock inte vana vid den elfte och trettonde övertonen, så denna bråkdel skulle inte låta konsonant för de flesta. På liknande sätt kunde felet i den elfte eller trettonde övertonen för det mesta elimineras av felet i den sjunde övertonen, men av samma anledning som tidigare skulle de flesta människor inte hitta de resulterande bråkens konsonant.

17- och 19-gränser

Den sjuttonde övertonen (17/16) är bara cirka 5 cent skarpare än en halvton i 12-TET. Den kan kombineras med 12-TET:s approximation av den tredje övertonen för att ge 17/12, vilket är, som nästa Pell approximation efter 7/5, bara cirka tre cent från den lika tempererade tritonen (kvadratroten av två), och 17/9, vilket är bara en cent från 12-TET:s stora sjua. Den nittonde övertonen är bara ungefär två och en halv cent plattare än tre av 12-TET:s halvtoner, så den kan på samma sätt kombineras med den tredje övertonen för att ge 19/12, vilket är ungefär fyra och en halv cent plattare än en likahärdad överton. moll sjätte och 19/18, vilket är ungefär sex och en halv cent plattare än en halvton. Men eftersom 17 och 19 är ganska stora för konsonantförhållanden och de flesta människor inte är bekanta med 17-gräns- och 19-gränsintervall, är 17-gräns- och 19-gränsintervall inte användbara för de flesta ändamål, så de kan troligen inte bedömas som spelar en roll i alla konsonanser av 12-TET.

Tabell

I följande tabell jämförs storlekarna för olika justa intervaller mot deras jämlika motsvarigheter, angivna som ett förhållande såväl som i cent . Skillnader på mindre än sex cent kan inte märkas av de flesta, och intervaller som är mer än ett kvarts steg, vilket i det här fallet är 25 cent, låter ostämt.

Antal steg	Anteckning går upp från C	Exakt värde i 12-TET	Decimalvärde i 12-TET	Lika tempererat ljud	Cents	Bara intonationsintervallnamn	Bara intonationsintervallfraktion	Rättvisa ljud	Cent i bara intonation	Skillnad
0	C	2 0 ⁄ 12 = 1	1	spela	0	Unison	1 ⁄ 1 = 1	spela	0	0
1	C ♯ eller D ♭	2 1 ⁄ 12 = 12 √ 2	1,05946...	spela	100	Septimal tredje ton	28 ⁄ 27 = 1,03703...	spela	62,96	-37.04
						Bara kromatisk halvton	25 ⁄ 24 = 1,04166...	Spela	70,67	-29.33
						Odecimal halvton	22 ⁄ 21 = 1,04761...	spela	80,54	-19.46
						Septimal kromatisk halvton	21 ⁄ 20 = 1,04	spela	84,47	-15.53
						Novendecimal kromatisk halvton	20 ⁄ 19 = 1,05263...	spela	88,80	-11.20
						Pythagoras diatoniska halvton	256 ⁄ 243 = 1,05349...	spela	90,22	-9,78
						Större kromatisk halvton	135 ⁄ 128 = 1,05468...	spela	92,18	-7,82
						Novendecimal diatonisk halvton	19 ⁄ 18 = 1,05555...	spela	93,60	-6.40
						Septadecimal kromatisk halvton	18 ⁄ 17 = 1,05882...	spela	98,95	-1.05
						Sjuttonde övertonen	17 ⁄ 16 = 1,0625...	spela	104,96	+4,96
						Bara diatonisk halvton	16 ⁄ 15 = 1,06666...	spela	111,73	+11,73
						Pythagoras kromatisk halvton	2187 ⁄ 2048 = 1,06787...	spela	113,69	+13,69
						Septimal diatonisk halvton	15 ⁄ 14 = 1,07142...	spela	119,44	+19,44
						Mindre tridecimal 2/3-ton	14 ⁄ 13 = 1,07692...	spela	128.30	+28.30
						Stor diatonisk halvton	27 ⁄ 25 = 1,08	spela	133,24	+33,24
2	D	2 2 ⁄ 12 = 6 √ 2	1,12246...	spela	200	Pythagoras minskade trea	65536 ⁄ 59049 = 1,10985...	spela	180,45	-19.55
						Mindre ton	10 ⁄ 9 = 1,11111...	spela	182,40	-17.60
						Stor ton	9 ⁄ 8 = 1,125	spela	203,91	+3,91
						Septimal helton	8 ⁄ 7 = 1,14285...	spela	231,17	+31,17
3	D ♯ eller E ♭	2 3 ⁄ 12 = 4 √ 2	1,18920...	spela	300	Septimal moll tredje	7 ⁄ 6 = 1,16666...	spela	266,87	-33.13
						Tridecimal moll tredje	13 ⁄ 11 = 1,18181...	spela	289,21	-10,79
						Pythagoras moll tredje	32 ⁄ 27 = 1,18518...	spela	294,13	-5,87
						Nittonde övertonen	19 ⁄ 16 = 1,1875	spela	297,51	-2,49
						Bara liten trea	6 ⁄ 5 = 1,2	spela	315,64	+15,64
						Pythagoras förstärkt tvåa	19683 ⁄ 16384 = 1,20135...	spela	317,60	+17,60
4	E	2 4 ⁄ 12 = 3 √ 2	1,25992...	spela	400	Pythagoras minskade fyran	8192 ⁄ 6561 = 1,24859...	spela	384,36	-15.64
						Bara stor trea	5 ⁄ 4 = 1,25	spela	386,31	-13.69
						Pythagoras major trea	81 ⁄ 64 = 1,265625	spela	407,82	+7,82
						Undecimal dur tredje	14 ⁄ 11 = 1,27272...	Spela	417,51	+17,51
						Septimal major tredje	9 ⁄ 7 = 1,28571...	spela	435,08	+35,08
5	F	2 5 ⁄ 12 = 12 √ 32	1,33484...	spela	500	Bara perfekt fjärde	4 ⁄ 3 = 1,33333...	spela	498,04	-1,96
						Pythagoras utökade trea	177147 ⁄ 131072 = 1,35152...	spela	521,51	+21,51
6	F ♯ eller G ♭	2 6 ⁄ 12 = √ 2	1,41421...	spela	600	Klassisk utökad fjärde	25 ⁄ 18 = 1,38888...	spela	568,72	-31.28
						Huygens triton	7 ⁄ 5 = 1,4	spela	582,51	-17.49
						Pythagoras minskade femma	1024 ⁄ 729 = 1,40466...	spela	588,27	-11.73
						Precis utökad fyra	45 ⁄ 32 = 1,40625	Spela	590,22	-9,78
						Bara minskad femma	64 ⁄ 45 = 1,42222...	spela	609,78	+9,78
						Pythagoras förstärkt fjärde	729 ⁄ 512 = 1,42382...	spela	611,73	+11,73
						Eulers triton	10 ⁄ 7 = 1,42857...	Spela	617,49	+17,49
						Klassisk förminskad femma	36 ⁄ 25 = 1,44	spela	631,28	+31,28
7	G	2 7 ⁄ 12 = 12 √ 128	1,49830...	spela	700	Pythagoras minskade sexa	262144 ⁄ 177147 = 1,47981...	spela	678,49	-21.51
						Bara perfekt femma	3 ⁄ 2 = 1,5	spela	701,96	+1,96
8	G ♯ eller A ♭	2 8 ⁄ 12 = 3 √ 4	1,58740...	spela	800	Septimal moll sjätte	14 ⁄ 9 = 1,55555...	spela	764,92	-35.08
						Undecimal moll sjätte	11 ⁄ 7 = 1,57142...	spela	782,49	-17.51
						Pythagoras moll sexa	128 ⁄ 81 = 1,58024...	spela	792,18	-7,82
						Bara mindre sjätte	8 ⁄ 5 = 1,6	spela	813,69	+13,69
						Pythagoras förstärkt femma	6561 ⁄ 4096 = 1,60180...	spela	815,64	+15,64
9	A	2 9 ⁄ 12 = 4 √ 8	1,68179...	spela	900	Pythagoras minskade som sjua	32768 ⁄ 19683 = 1,66478...	spela	882,40	-17.60
						Bara major sexa	5 ⁄ 3 = 1,66666...	spela	884,36	-15.64
						Nittonde underharmonik	32 ⁄ 19 = 1,68421...	spela	902,49	+2,49
						Pythagoras major sexa	27 ⁄ 16 = 1,6875	spela	905,87	+5,87
						Septimal major sjätte	12 ⁄ 7 = 1,71428...	Spela	933,13	+33,13
10	A ♯ eller B ♭	2 10 ⁄ 12 = 6 √ 32	1,78179...	spela	1000	Harmonisk sjua	7 ⁄ 4 = 1,75	spela	968,83	-31.17
						Pythagoras moll sjunde	16 ⁄ 9 = 1,77777...	spela	996,09	-3,91
						Stor liten sjua	9 ⁄ 5 = 1,8	spela	1017,60	+17,60
						Pythagoras förstärkt sexa	59049 ⁄ 32768 = 1,80203...	spela	1019,55	+19,55
11	B	2 11 ⁄ 12 = 12 √ 2048	1,88774...	spela	1100	Tridecimal neutral sjua	13 ⁄ 7 = 1,85714...	spela	1071,70	-28.30
						Pythagoras förminskad oktav	4096 ⁄ 2187 = 1,87288...	spela	1086,31	-13.69
						Bara stor sjua	15 ⁄ 8 = 1,875	spela	1088,27	-11.73
						Sjuttonde undertonen	32 ⁄ 17 = 1,88235...	spela	1095,04	-4,96
						Pythagoras dur sjunde	243 ⁄ 128 = 1,89843...	spela	1109,78	+9,78
						Septimal major sjunde	27 ⁄ 14 = 1,92857...	spela	1137.04	+37,04
12	C	2 12 ⁄ 12 = 2	2	spela	1200	Oktav	2 ⁄ 1 = 2	spela	1200,00	0

Kommateken

12-TET tempererar flera kommatecken , vilket betyder att det finns flera bråk nära 1 ⁄ 1 som behandlas som 1 ⁄ 1 av 12-TET på grund av dess mappning av olika bråk till samma intervall med lika tempererade intervall. Till exempel är 729 ⁄ 512 ( 3 ⁶ ⁄ 2 ⁹ ) och 1024 ⁄ 729 ( 2 ¹⁰ ⁄ 3 ⁶ ) var och en mappad till tritonen, så de behandlas som samma intervall; därför är deras kvot, 531441 ⁄ 524288 ( 3 ¹² ⁄ 2 ¹⁹ ) mappad till/behandlas som unisont. Detta är det pythagoriska kommatecken och det är 12-TET:s enda 3-gränskomma. Men när man ökar primtalsgränsen och inkluderar fler intervall, ökar antalet kommatecken. 12-TET:s viktigaste kommatecken med fem gränser är 81 ⁄ 80 ( 3 ⁴ ⁄ 2 ⁴ × 5 ¹ ), vilket är känt som det syntoniska kommatecken och är faktorn mellan pythagoras tredjedelar och sjättedelar och deras rättvisa motsvarigheter. 12-TET:s andra 5-limit-komma inkluderar:

• Schisma : 32805 ⁄ 32768 = 3 ⁸ × 5 ¹ ⁄ 2 ¹⁵ =( 531441 ⁄ 524288 ) ¹ ×( 81 ⁄ 80 ) ⁻¹
• Diaschisma : 2048 ⁄ 2025 = 2 ¹¹ ⁄ 3 ⁴ × 5 ² =( 531441 ⁄ 524288 ) ⁻¹ ×( 81 ⁄ 80 ) ²
• Mindre diesis : 128 ⁄ 125 = 2 ⁷ ⁄ 5 ³ =( 531441 ⁄ 524288 ) ⁻¹ ×( 81 ⁄ 80 ) ³
• Större diesis : 648 ⁄ 625 = 2 ³ × 3 ⁴ ⁄ 5 ⁴ =( 531441 ⁄ 524288 ) ⁻¹ ×( 81 ⁄ 80 ) ⁴

Ett av de 7-gränskomma som 12-TET dämpar är septimal kleisma , som är lika med 225 ⁄ 224 , eller 3 ² × 5 ² ⁄ 2 ⁵ × 7 ¹ . 12-TETs andra 7-limit-komma inkluderar:

• Septimalt semikomma : 126 ⁄ 125 = 2 ¹ × 3 ² × 7 ¹ ⁄ 5 ³ =( 81 ⁄ 80 ) ¹ ×( 225 ⁄ 224 ) ⁻¹
• Archytas kommatecken : 64 ⁄ 63 = 2 ⁶ ⁄ 3 ² × 7 ¹ =( 531441 ⁄ 524288 ) ⁻¹ ×( 81 ⁄ 80 ) ² ×( 225 ⁄ 224 ) ¹
• Septimal kvartston : 36 ⁄ 35 = 2 ² × 3 ² ⁄ 5 ¹ × 7 ¹ =( 531441 ⁄ 524288 ) ⁻¹ ×( 81 ⁄ 80 ) ³ ×( 225 ⁄ 224 ) ¹
• Jubilisma : 50 ⁄ 49 = 2 ¹ × 5 ² ⁄ 7 ² =( 531441 ⁄ 524288 ) ⁻¹ ×( 81 ⁄ 80 ) ² ×( 225 ⁄ 224 ) ²

Liknande trimsystem

Historiskt har flera stämningssystem använts som kan ses som små variationer av 12-TEDO, med tolv toner per oktav men med viss variation mellan intervallstorlekar så att tonerna inte är helt jämnt fördelade. Ett exempel på detta är en skala med tre gränser där lika tempererade perfekta kvintdelar på 700 cent ersätts med rättvisa perfekta kvintdelar på 701,955 cent. Eftersom de två intervallen skiljer sig med mindre än 2 cent, eller 1 ⁄ 600 av en oktav, är de två skalorna väldigt lika. Faktum är att kineserna utvecklade 3-limit bara intonation minst ett sekel innan He Chengtian skapade sekvensen av 12-TEDO. Likaså var pythagoras stämning, som utvecklades av antika greker, det dominerande systemet i Europa tills under renässansen, då européer insåg att dissonanta intervaller som 81 ⁄ 64 kunde göras mer konsonanta genom att temperera dem till enklare förhållanden som 5 ⁄ 4 , vilket resulterade i att Europa utvecklade en serie medeltonstemperament som ändrade intervallstorlekarna något men som fortfarande kunde ses som en ungefärlig 12-TEDO. På grund av mellantonstemperamentens tendens att koncentrera fel på en enharmonisk perfekt kvint, vilket gör det mycket dissonant , skapade europeiska musikteoretiker, såsom Andreas Werckmeister, Johann Philipp Kirnberger, Francesco Antonio Vallotti och Thomas Young, olika brunnstemperament med målet att dela upp kommatecken för att minska dissonansen i de värst drabbade intervallen. Werckmeister och Kirnberger var var och en missnöjd med sitt första temperament och skapade därför flera temperament, de senare temperamenten närmade sig mer lika temperament än de tidigare temperamenten. På samma sätt övergick Europa som helhet gradvis från elak ton och brunnstemperament till 12-TEDO, systemet som det fortfarande använder idag.

Delmängder

Se även: Skala (musik)

Medan vissa typer av musik, som serialism , använder alla tolv toner av 12-TEDO, använder de flesta musik endast toner från en viss delmängd av 12-TEDO som kallas en skala. Det finns många olika typer av vågar.

Den mest populära typen av våg i 12-TEDO är meantone. Meantone hänvisar till varje skala där alla dess toner är konsekutiva på cirkeln av femtedelar. Meantone skalor av olika storlek finns, och vissa meantone-skalor som används inkluderar fem-noter meantone , sju-note meantone och nio-note meantone . Meantone är närvarande i designen av västerländska instrument. Till exempel är tangenterna på ett piano och dess föregångare strukturerade så att de vita tangenterna bildar en sju-toners medeltonsskala och de svarta tangenterna bildar en femtoners medeltonsskala. Ett annat exempel är att gitarrer och andra stränginstrument med minst fem strängar vanligtvis är stämda så att deras öppna strängar bildar en femtoners medeltonsskala.

Andra skalor som används i 12-TEDO inkluderar den stigande melodiska mollskalan , den harmoniska mollskalan , den harmoniska durskalan , den förminskade skalan och in-skalan .

Se även

• Lika temperament
• Bara intonation
• Musikalisk akustik (musikens fysik)
• Musik och matematik
• Mikrotonal musik
• Lista över mellantonsintervall
• Diatonisk och kromatisk
• Elektronisk tuner
• Musikalisk stämning

Källor

•   Barbour, James Murray (2004). Tuning and Temperament: A Historical Survey . Courier Corporation. ISBN 978-0-486-43406-3 .
•   Benward, Bruce; Saker, Marilyn (2003). Musik i teori och praktik . Vol. 1. McGraw-Hill. ISBN 978-0-07-294261-3 .
•   Cho, Gene J. (2003). Upptäckten av musikaliskt lika temperament i Kina och Europa under 1500-talet . E. Mellen Press. ISBN 978-0-7734-6941-9 .
• Cho, Gene J. (2010). " Betydelsen av upptäckten av det musikaliska jämlika temperamentet i kulturhistorien" . Journal of Xinghai Conservatory of Music .
•   Christensen, Thomas (2002). The Cambridge History of Western Music Theory . Cambridge University Press. ISBN 978-0-521-62371-1 .
•   Cohen, H. Floris (1987). "Simon Stevins lika uppdelning av oktaven". Vetenskapens annaler . Informa UK Limited. 44 (5): 471–488. doi : 10.1080/00033798700200311 . ISSN 0003-3790 .
•   de Gorzanis, G. (1981). Intabolatura di liuto: I-III . Intabolatura di liuto: I-III (på italienska). Minkoff. ISBN 978-2-8266-0721-2 .
• Di Veroli, Claudio (2009). Ojämlika temperament: teori, historia och praktik (2:a uppl.). Bray, Irland: Bray Baroque.
• Galilei, Vincenzo (1584). Il Fronimo . Venedig: Girolamo Scotto .
• Hart, Roger (1998), Quantifying Ritual: Political Cosmology, Courtly Music, and Precision Mathematics in Seventeenth-Century China, Departments of History and Asian Studies, University of Texas, Austin, arkiverad från originalet 2012-03-05 , hämtad 2012-03-20
•   Jorgens, Elise Bickford (1986). Engelsk sång, 1600-1675: Faksimiler av tjugosex manuskript och en upplaga av texterna . Krans. ISBN 9780824082314 .
•   Kuttner, Fritz A. (maj 1975). "Prins Chu Tsai-Yüs liv och arbete: en omvärdering av hans bidrag till teorin om lika temperament" ( PDF) . Etnomusikologi . 19 (2): 163–206. doi : 10.2307/850355 . JSTOR 850355 .
•   Kwang-chih Chang; Pingfang Xu; Liancheng Lu (2005). "Den östra Zhou och regionalismens tillväxt". Bildandet av kinesisk civilisation: ett arkeologiskt perspektiv . Xu Pingfang, Shao Wangping, Zhang Zhongpei, Wang Renxiang. Yale University Press. ISBN 978-0-300-09382-7 .
• Lienhard, John H. (1997). "Jämlikt temperament" . Motorerna i vår uppfinningsrikedom . University of Houston . Hämtad 2014-10-05 .
• Moody, Richard (februari 2003). "Early Equal Temperament, An Aural Perspective: Claude Montal 1836". Piano Technicians Journal . Kansas City.
•   Needham, Joseph ; Ling, Wang; Robinson, Kenneth G. (1962). Vetenskap och civilisation i Kina . Volym 4 - Del 1. Cambridge University Press. ISBN 978-0-521-05802-5 .
• Needham, Joseph; Ronan, Colin A. (1978). Den kortare vetenskapen och civilisationen i Kina . Volym 4 - Del 1. Cambridge University Press.
•   Partch, Harry (1979). Genesis of a Music (2:a upplagan). Da Capo Press. ISBN 0-306-80106-X .
•   Robinson, Kenneth (1980). En kritisk studie av Chu Tsai-yüs bidrag till teorin om lika temperament i kinesisk musik . Volym 9 av Sinologica Coloniensia. Wiesbaden: Steiner. ISBN 978-3-515-02732-8 .
•   Sethares, William A. (2005). Tuning, Timbre, Spectrum, Scale (2:a upplagan). London: Springer-Verlag. ISBN 1-85233-797-4 .
• Det är sant, Timothy (2018). "Kampen mellan oklanderlig intonation och maximerad modulering" . Musikaliska erbjudanden . 9 (2): 61–74. doi : 10.15385/jmo.2018.9.2.2 .
• von Helmholtz, Hermann ; Ellis, Alexander J. (1885). Om förnimmelser av ton som fysiologisk grund för musikteori ( 2:a uppl.). London: Longmans, Green.
• Wilson, John (1997). "Trettio preludier totalt (24) tonarter för luta [DP 49]" . Diapasonpressen . Hämtad 27 oktober 2020 .

Vidare läsning

• Duffin, Ross W. Hur lika temperament förstörde harmoni (och varför du borde bry dig) . WW Norton & Company, 2007.
•   Jörgensen, Owen. Tuning . Michigan State University Press, 1991. ISBN 0-87013-290-3
•   Khramov, Mykhaylo. "Approximation of 5-limit just intonation. Computer MIDI Modeling in Negative Systems of Equal Divisions of the Octave", Proceedings of the International Conference SIGMAP-2008 , 26–29 juli 2008, Porto , s. 181–184 , ISBN 978-989-8111-60-9
• Surjodiningrat, W., Sudarjana, PJ och Susanto, A. (1972) Tonmätningar av enastående javanesiska gamelans i Jogjakarta och Surakarta, Gadjah Mada University Press, Jogjakarta 1972. Citerad på https://web.archive.org/web/ 20050127000731/http://web.telia.com/~u57011259/pelog_main.htm . Hämtad 19 maj 2006.
• Stewart, PJ (2006) "From Galaxy to Galaxy: Music of the Spheres" [ 1]
• Sensations of Tone ett grundläggande verk om akustik och ljuduppfattning av Hermann von Helmholtz. Speciellt bilaga XX: Tillägg av översättaren, sidorna 430–556, (pdf sidorna 451–577)]

externa länkar

• Xenharmonic wiki om EDOs vs Equal Temperaments
• Huygens-Fokkers stiftelse Centrum för mikrotonal musik
• A.Orlandini: Musikakustik
• "Temperament" från A supplement till Mr. Chambers' cyclopædia (1753)
• Barbieri, Patrizio. Enharmoniska instrument och musik, 1470–1900 Arkiverad 2009-02-15 på Wayback Machine . (2008) Latina, Il Levante Libreria Editrice
• Fractal Microtonal Music , Jim Kukula .
• Alla befintliga 1700-talscitat om JS Bach och temperament
• Dominic Eckersley: " Rosetta Revisited: Bach's Very Ordinary Temperament "
• Well Temperaments, baserat på Werckmeister-definitionen
• _ _ _ FAVORERADE KARDINALITER AV KALER AV P ETER B UCH