Pythagoras kommatecken

Pythagoras kommatecken (531441:524288) på C   Play .

Pythagoras kommatecken på C med Ben Johnstons notation . Tonen som visas som lägre på notstaven (B ♯ +++ ) är något högre i tonhöjd (än C ♮ ).

Pythagoras kommatecken ( PC ) definieras i Pythagoras stämning som skillnad mellan halvtoner (A1 – m2), eller intervall mellan enharmoniskt ekvivalenta toner (från D ♭ till C ♯ ). Den förminskade sekunden har samma bredd men motsatt riktning (från till C ♯ till D ♭ ).

I musikalisk stämning är det pytagoreiska kommatecken (eller ditoniska kommatecken ), uppkallat efter den forntida matematikern och filosofen Pythagoras , det lilla intervallet ( eller kommatecken ) som existerar i pythagoras stämning mellan två enharmoniskt ekvivalenta toner som C och B ♯ (   Spela ), eller D ♭ och C ♯ . Det är lika med frekvensförhållandet (1,5) ¹² ⁄ 2 ⁷ = 531441 ⁄ 524288 ≈ 1,01364, eller cirka 23,46 cent , ungefär en fjärdedel av en halvton (mellan 75:74 och 74:73). Det kommatecken som musikaliska temperament ofta refererar till temperering är det pytagoreiska kommatecken.

Det pythagoriska kommatecken kan också definieras som skillnaden mellan en pytagoreisk apotom och en pytagoreisk limma (dvs mellan en kromatisk och en diatonisk halvton , som bestäms i pythagoras stämning), eller skillnaden mellan tolv perfekta kvintdelar och sju oktaver , eller skillnaden mellan tre pytagoreiska ditoner och en oktav (detta är anledningen till att det pytagoreiska kommatecken också kallas ditoniskt komma ).

Den förminskade sekunden , i pythagoreisk stämning, definieras som skillnaden mellan limma och apotom. Det sammanfaller därför med motsatsen till ett pytagoreiskt kommatecken och kan ses som ett nedåtgående pytagoreiskt kommatecken (t.ex. från C ♯ till D ♭ ), lika med cirka -23,46 cent.

Härledning

Som beskrivits i inledningen kan det pythagoriska kommatecken härledas på flera sätt:

• Skillnad mellan två enharmoniskt ekvivalenta toner i en pytagoreisk skala, som C och B ♯ (   Spela ), eller D ♭ och C ♯ (se nedan ).
• Skillnaden mellan Pythagoras apotom och Pythagoras limma .
• Skillnaden mellan tolv perfekta kvintdelar och sju oktaver .
• Skillnad mellan tre Pythagoras ditoner ( stora tredjedelar ) och en oktav.

En precis perfekt femma har ett frekvensförhållande på 3:2. Den används i pytagoreisk stämning, tillsammans med oktaven, som en måttstock för att definiera, med avseende på en given initial ton, frekvensförhållandet för någon annan ton.

Apotome och limma är de två typerna av halvtoner som definieras i Pythagoras stämning. Apotomen (cirka 113,69 cent, t.ex. från C till C ♯ ) är nämligen den kromatiska halvtonen, eller förstärkt unison (A1), medan limma (cirka 90,23 cent, t.ex. från C till D ♭ ) är den diatoniska halvtonen, eller moll. sekund (m2).

En ditone (eller ha som huvudämne tredje ) är ett intervall som bildas av två ha som huvudämne tonar . I pythagoras stämning har en durton en storlek på cirka 203,9 cent (frekvensförhållande 9:8), sålunda är en pythagoras diton cirka 407,8 cent.

Oktaver (7 × 1200 = 8400) mot femtedelar (12 × 701,96 = 8423,52), avbildade som med Cuisenaire-stavar (röd (2) används för 1200, svart (7) används för 701,96).

Oktaver (1 × 1200 = 1200) kontra ditoner (3 × 407,82 = 1223,46), avbildade som med Cuisenaire-stavar (röd (2) används för 1200, magenta (4) används för 407,82).

Storlek

Storleken på ett pytagoreiskt kommatecken, mätt i cent , är

${\displaystyle {\hbox{apotome}}-{\hbox{limma}}\approx 113,69-90,23\approx 23,46~s}}\hbox!$

eller mer exakt, i termer av frekvensförhållanden :

${\frac {\hbox{apotome}}{\hbox{apotome}}{\}}{lim ^{7}/2^{11}}{2^{8}/3^{5}}}={\frac {3^{12}}{2^{19}}}={\frac {531441 }{524288}}=1,0136432647705078125\!$

Det pytagoreiska kommatecken som visas som gapet (på höger sida) som gör att en 12-uddig stjärna misslyckas med att stängas, vilken stjärna representerar den pytagoreiska skalan; varje rad representerar en precis perfekt femma. Det gapet har en central vinkel på 7,038 grader, vilket är 23,46% av 30 grader.

Cirkel av femtedelar och enharmonisk förändring

Pythagoras kommatecken som tolv rättvist inställda perfekta femtedelar i Ben Johnston-notation.

Det pytagoreiska kommatecken kan också ses som diskrepansen mellan tolv rättvist inställda perfekta kvintdelar (förhållande 3:2) (   spel ) och sju oktaver (förhållande 2:1):

${\frac {\hbox{twelve oc\hvesta}(even oc\hvesta}) {\tfrac {3}{2}}\right)^{12}\!\!{\Big /}\,2^{7}={\frac {3^{12}}{2^{19} }}={\frac {531441}{524288}}=1,0136432647705078125\!$

Stigande med perfekta femtedelar Notera Femte Frekvensförhållande Decimalkvot C 0 1 : 1 1 G 1 3 : 2 1.5 D 2 9 : 4 2,25 A 3 27 : 8 3,375 E 4 81:16 _ _ 5,0625 B 5 243 : 32 7,59375 F ♯ 6 729 : 64 11.390625 C ♯ 7 2187 : 128 17.0859375 G ♯ 8 6561 : 256 25.62890625 D ♯ 9 19683 : 512 38.443359375 A ♯ 10 59049 : 1024 57.6650390625 E ♯ 11 177147 : 2048 86.49755859375 B ♯ (≈ C) 12 531441 : 4096 129.746337890625

Stigande med oktaver Notera Oktav Frekvensförhållande C 0 1 : 1 C 1 2 : 1 C 2 4 : 1 C 3 8 : 1 C 4 16 : 1 C 5 32 : 1 C 6 64 : 1 C 7 128 : 1

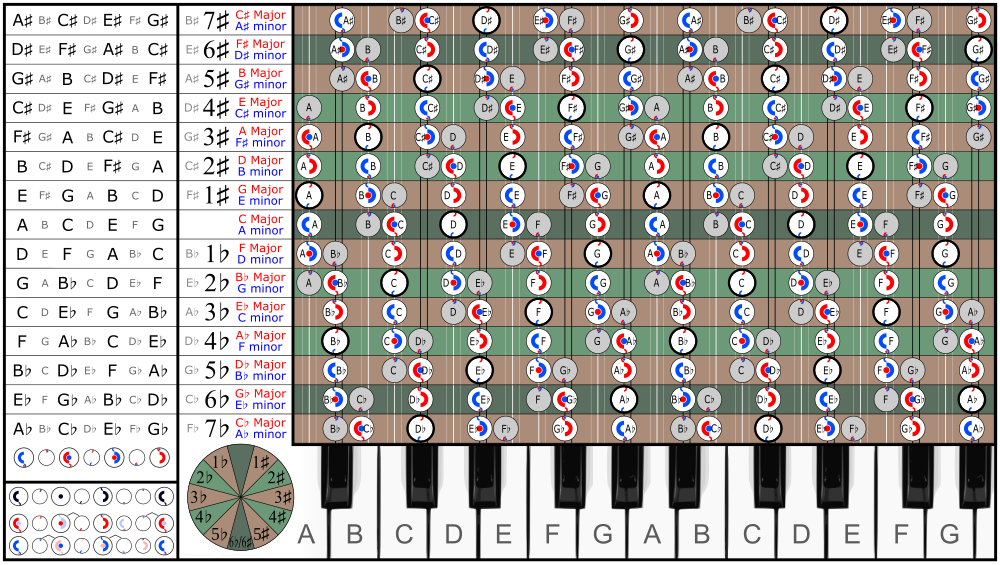
I följande tabell över musikskalor i femtedelscirkeln är det pytagoreiska kommatecken synligt som det lilla intervallet mellan t.ex. F ♯ och G ♭ . Att gå runt femtedelscirkeln med bara intervall resulterar i en kommapump med det pythagoriska kommatecken.

6 ♭ och 6 ♯ skalorna* är inte identiska - även om de finns på pianoklaviaturen - men ♭ -skalan är ett pytagoreiskt kommatecken lägre. Att bortse från denna skillnad leder till enharmonisk förändring .

* Skalorna 7 ♭ och 5 ♯ , 5 ♭ respektive 7 ♯ skiljer sig åt på samma sätt med ett pytagoreiskt kommatecken. Skalor med sju tillfälligheter används sällan, eftersom de enharmoniska skalorna med fem tillfälligheter behandlas som likvärdiga.

Detta intervall har allvarliga konsekvenser för de olika stämningsscheman i den kromatiska skalan , eftersom i västerländsk musik behandlas 12 perfekta kvintdelar och sju oktaver som samma intervall. Lika temperament , idag det vanligaste stämningssystemet som används i väst, förenade detta genom att platta till varje femtedel med en tolftedel av ett pythagoras kommatecken (ungefär 2 cent), vilket gav perfekta oktaver.

Ett annat sätt att uttrycka detta är att den bara femte har ett frekvensförhållande (jämfört med toniken) på 3:2 eller 1,5 till 1, medan den sjunde halvtonen (baserat på 12 lika logaritmiska divisioner av en oktav) är den sjunde potensen av tolfte roten av två eller 1,4983... till 1, vilket inte är riktigt detsamma (ut med cirka 0,1%). Ta bara femman till tolfte potensen, subtrahera sedan sju oktaver och du får det pythagoriska kommatecken (cirka 1,4 % skillnad).

Historia

Den första som nämnde kommatets proportion på 531441:524288 var Euklid , som utgår från hela tonen i Pythagoras stämning med förhållandet 9:8, oktaven med förhållandet 2:1 och ett tal A = 262144. Han drar slutsatsen att en höjning av detta tal med sex hela toner ger ett värde G som är större än det som erhålls genom att höja det med en oktav (två gånger A). Han ger G till 531441. De nödvändiga beräkningarna lyder:

Beräkning av G:

$262144\cdot \left(\textstyle {\frac {9}{8}}\right)^{6}=531441$

Beräkning av det dubbla av A:

$262144\cdot \left(\textstyle {\frac {2}{1}}\right)^{1}=524288$

Kinesiska matematiker hade varit medvetna om det pythagoreiska kommatecken så tidigt som 122 f.Kr. (dess beräkning är detaljerad i Huainanzi ), och cirka 50 f.Kr. upptäckte Ching Fang att om cykeln med perfekta femtedelar fortsatte efter 12 ända till 53, skillnaden mellan denna 53:e tonhöjd och startplanen skulle vara mycket mindre än det pythagoriska kommatecken. Detta mycket mindre intervall kallades senare Mercators kommatecken ( se: historia med 53 lika temperament ).

I George Russells Lydian Chromatic Concept of Tonal Organization (1953) är halva steget mellan Lydian Tonic och ♭ 2 i hans Altered Major och Minor Auxiliary Diminished Blues-skalor teoretiskt baserat på intervallet för ett pythagoreiskt kommatecken.

Se även

• Syntoniskt kommatecken
• Schisma
• Holdrian kommatecken