Nollsymmetrisk graf

Den minsta nollsymmetriska grafen, med 18 hörn och 27 kanter

Den trunkerade kuboktaedern , en nollsymmetrisk polyeder

Graffamiljer definierade av deras automorfismer
distanstransitiv	→	avstånd-regelbundet	←	starkt regelbunden
↓
symmetrisk (bågtransitiv)	←	t -transitiv, t ≥ 2		snedsymmetrisk
↓
(om ansluten) vertex- och kanttransitiv	→	kanttransitiv och regelbunden	→	kanttransitiv
↓		↓		↓
vertextransitiv	→	regelbunden	→	(om tvådelad) biregelbunden
↑
Cayley graf	←	nollsymmetrisk		asymmetrisk

Inom det matematiska området för grafteorin är en nollsymmetrisk graf en sammankopplad graf där varje vertex har exakt tre infallande kanter och för varje två hörn finns det en unik symmetri som tar en vertex till den andra. En sådan graf är en vertextransitiv graf men kan inte vara en kanttransitiv graf : antalet symmetrier är lika med antalet hörn, för få för att ta varje kant till varannan kant.

Den minsta nollsymmetriska grafen med två kantbanor

Namnet för denna klass av grafer myntades av RM Foster i ett brev från 1966 till HSM Coxeter . I gruppteorisammanhang kallas nollsymmetriska grafer också för grafiska reguljära representationer av deras symmetrigrupper.

Exempel

Den minsta nollsymmetriska grafen är en icke-planär graf med 18 hörn. Dess LCF-notation är [5,−5] ⁹ .

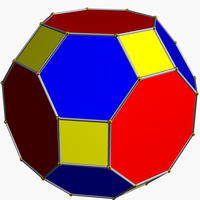
Bland plana grafer är de trunkerade kuboktaedriska och trunkerade icosidodekaedriska graferna också nollsymmetriska.

Dessa exempel är alla tvådelade grafer . Det finns dock större exempel på nollsymmetriska grafer som inte är tvådelade.

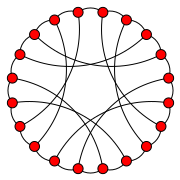
Dessa exempel har också tre olika symmetriklasser (banor) av kanter. Det finns dock nollsymmetriska grafer med bara två kanter. Den minsta grafen har 20 hörn, med LCF-notation [6,6,-6,-6] ⁵ .

Egenskaper

Varje finit nollsymmetrisk graf är en Cayley-graf , en egenskap som inte alltid gäller för kubiska vertextransitiva grafer mer generellt och som hjälper till med lösningen av kombinatoriska uppräkningsuppgifter gällande nollsymmetriska grafer. Det finns 97687 nollsymmetriska grafer på upp till 1280 hörn. Dessa grafer utgör 89 % av de kubiska Cayley-graferna och 88 % av alla anslutna vertextransitiva kubiska grafer på samma antal hörn.

Olöst problem i matematik :

Innehåller varje finit nollsymmetrisk graf en Hamiltonsk cykel ?

(fler olösta problem i matematik)

Alla kända ändliga anslutna nollsymmetriska grafer innehåller en Hamiltonsk cykel , men det är okänt om varje ändligt ansluten nollsymmetrisk graf nödvändigtvis är Hamiltonsk. Detta är ett specialfall av Lovász-förmodan att (med fem kända undantag, varav inget är nollsymmetriskt) varje finit ansluten vertextransitiv graf och varje finit Cayley-graf är Hamiltonian.

Se även

• Semi-symmetrisk graf , grafer som har symmetri mellan varannan kanter men inte mellan varannan hörn (omvänd rollerna för kanter och hörn i definitionen av nollsymmetriska grafer)