Variansanalys

Variansanalys ( ANOVA ) är en samling statistiska modeller och deras associerade uppskattningsprocedurer (som "variationen" mellan och mellan grupper) som används för att analysera skillnaderna mellan medelvärden. ANOVA utvecklades av statistikern Ronald Fisher . ANOVA är baserad på lagen om total varians , där den observerade variansen i en viss variabel är uppdelad i komponenter som kan hänföras till olika variationskällor. I sin enklaste form tillhandahåller ANOVA ett statistiskt test av om två eller flera populationsmedelvärden är lika, och generaliserar därför t -testet bortom två medelvärden. Med andra ord, ANOVA används för att testa skillnaden mellan två eller flera medel.

Historia

Medan variansanalysen nådde förverkligande på 1900-talet sträcker sig tidigare århundraden in i det förflutna enligt Stigler. Dessa inkluderar hypotestestning, uppdelning av kvadratsummor, experimentella tekniker och den additiva modellen. Laplace utförde hypotestestning på 1770-talet. Runt 1800 utvecklade Laplace och Gauss den minsta kvadratiska metoden för att kombinera observationer, som förbättrade metoder som då användes inom astronomi och geodesi . Det initierade också mycket studier av bidragen till kvadratsummor. Laplace visste hur man uppskattar en varians från en kvarvarande (snarare än en total) summa av kvadrater. År 1827 använde Laplace minsta kvadratmetoder för att ta itu med ANOVA-problem angående mätningar av atmosfäriskt tidvatten. Före 1800 hade astronomer isolerat observationsfel som härrörde från reaktionstider ("den personliga ekvationen ") och hade utvecklat metoder för att minska felen. De experimentella metoderna som användes i studien av den personliga ekvationen accepterades senare av det framväxande psykologinområdet som utvecklade starka (fullfaktoriella) experimentella metoder till vilka randomisering och blindning snart lades till. En vältalig icke-matematisk förklaring av modellen för additiva effekter fanns tillgänglig 1885.

Ronald Fisher introducerade termen varians och föreslog dess formella analys i en artikel 1918 The Correlation Between Relatives on the supposition of Mendelian Inheritance . Hans första tillämpning av variansanalysen publicerades 1921. Variansanalys blev allmänt känd efter att ha inkluderats i Fishers bok 1925 Statistical Methods for Research Workers .

Randomiseringsmodeller har utvecklats av flera forskare. Den första publicerades på polska av Jerzy Neyman 1923.

Exempel

Passar inte: Ung vs gammal, och korthårig vs långhårig

Rättvis passform: Pet vs Working ras och mindre atletisk kontra mer atletisk

Mycket bra passform: Vikt per ras

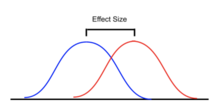
Variansanalysen kan användas för att beskriva i övrigt komplexa relationer mellan variabler. En hundutställning ger ett exempel. En hundutställning är inte ett slumpmässigt urval av rasen: den är vanligtvis begränsad till hundar som är vuxna, renrasiga och exemplariska. Ett histogram av hundvikter från en utställning kan troligen vara ganska komplext, som den gul-orange fördelningen som visas i illustrationerna. Anta att vi ville förutsäga vikten på en hund baserat på en viss uppsättning egenskaper hos varje hund. Ett sätt att göra det är att förklara viktfördelningen genom att dela upp hundpopulationen i grupper utifrån dessa egenskaper. En framgångsrik gruppering kommer att dela upp hundar så att (a) varje grupp har en låg varians av hundvikter (vilket betyder att gruppen är relativt homogen) och (b) medelvärdet för varje grupp är distinkt (om två grupper har samma medelvärde, då är inte rimligt att dra slutsatsen att grupperna faktiskt är separata på något meningsfullt sätt).

I illustrationerna till höger identifieras grupper som X ₁ , X ₂ , etc. I den första illustrationen delas hundarna in efter produkten (interaktionen) av två binära grupperingar: ung vs gammal, och korthårig vs. -håriga (t.ex. grupp 1 är unga, korthåriga hundar, grupp 2 är unga, långhåriga hundar, etc.). Eftersom fördelningarna av hundvikt inom var och en av grupperna (visad i blått) har en relativt stor varians, och eftersom medelvärdena är mycket lika mellan grupperna, ger gruppering av hundar efter dessa egenskaper inte ett effektivt sätt att förklara variationen i hundvikter : Att veta vilken grupp en hund är i tillåter oss inte att förutsäga vikten mycket bättre än att bara veta att hunden är på en hundutställning. Denna gruppering kan således inte förklara variationen i den totala fördelningen (gul-orange).

Ett försök att förklara viktfördelningen genom att gruppera hundar som sällskapsdjur vs arbetsras och mindre atletisk vs mer atletisk skulle förmodligen vara något mer framgångsrikt (fair fit). De tyngsta utställningshundarna är sannolikt stora, starka arbetarraser, medan raser som hålls som husdjur tenderar att vara mindre och därmed lättare. Som visas av den andra illustrationen har fördelningarna avvikelser som är betydligt mindre än i det första fallet, och medelvärdena är mer urskiljbara. Men den betydande överlappningen av distributioner, till exempel, gör att vi inte kan skilja X ₁ och X ₂ tillförlitligt. Att gruppera hundar enligt en myntflik kan ge uppdelningar som ser likadana ut.

Ett försök att förklara vikt efter ras kommer sannolikt att ge en mycket bra passform. Alla Chihuahuas är lätta och alla St Bernards är tunga. Skillnaden i vikt mellan Setters och Pointers motiverar inte separata raser. Variansanalysen ger de formella verktygen för att motivera dessa intuitiva bedömningar. En vanlig användning av metoden är analys av experimentella data eller utveckling av modeller. Metoden har vissa fördelar jämfört med korrelation: alla data måste inte vara numeriska och ett resultat av metoden är en bedömning av förtroendet för ett förklarande samband.

Klasser av modeller

Det finns tre klasser av modeller som används i variansanalysen, och dessa beskrivs här.

Modeller med fasta effekter

Huvudartikel: Modell med fasta effekter

Modellen med fasta effekter (klass I) för variansanalys gäller situationer där försöksledaren tillämpar en eller flera behandlingar på försökspersonerna för att se om svarsvariabelvärdena ändras . Detta tillåter försöksledaren att uppskatta intervallen för svarsvariabelvärden som behandlingen skulle generera i befolkningen som helhet.

Fasta effekter vs slumpmässiga effekter

Modeller med slumpmässiga effekter

Huvudartikel: Modell för slumpmässiga effekter

Slumpmässiga effekter modell (klass II) används när behandlingarna inte är fixerade. Detta inträffar när de olika faktornivåerna provtas från en större population. Eftersom nivåerna i sig är slumpvariabler skiljer sig vissa antaganden och metoden för att kontrastera behandlingarna (en multivariabel generalisering av enkla skillnader) från modellen med fasta effekter.

Modeller med blandade effekter

Huvudartikel: Blandad modell

En blandad effektmodell (klass III) innehåller experimentella faktorer av både fixerade och slumpmässiga effekter, med lämpligt olika tolkningar och analyser för de två typerna.

Exempel

Undervisningsexperiment kan utföras av en högskola eller universitetsavdelning för att hitta en bra inledande lärobok, där varje text betraktas som en behandling. Modellen med fasta effekter skulle jämföra en lista med kandidattexter. Modellen med slumpmässiga effekter skulle avgöra om det finns viktiga skillnader mellan en lista med slumpmässigt utvalda texter. Modellen med blandade effekter skulle jämföra de (fasta) befintliga texterna med slumpmässigt utvalda alternativ.

Att definiera fasta och slumpmässiga effekter har visat sig svårfångat, med konkurrerande definitioner som förmodligen leder till ett språkligt gräv.

Antaganden

Variansanalysen har studerats från flera tillvägagångssätt, varav den vanligaste använder en linjär modell som relaterar responsen till behandlingarna och blockeringen. Observera att modellen är linjär i parametrar men kan vara olinjär över faktornivåer. Tolkning är lätt när data är balanserad över faktorer men mycket djupare förståelse behövs för obalanserad data.

Läroboksanalys med normalfördelning

Variansanalysen kan presenteras i termer av en linjär modell , som gör följande antaganden om sannolikhetsfördelningen av svaren:

• Oberoende av observationer – detta är ett antagande av modellen som förenklar den statistiska analysen.
• Normalitet – fördelningarna av residualerna är normala .
• Likhet (eller "homogenitet") av varianser, kallad homoskedasticitet - variansen av data i grupper bör vara densamma.

Läroboksmodellens separata antaganden innebär att felen är oberoende, identiskt och normalfördelade för modeller med fasta effekter, det vill säga att felen ( ${\displaystyle \varepsilon } )$ är oberoende och

$$\varepsilon \thicksim N(0,\sigma ^{2}).$$

Randomiseringsbaserad analys

Se även: Slumpmässig uppgift och Randomiseringstest

I ett randomiserat kontrollerat experiment tilldelas behandlingarna slumpmässigt till experimentella enheter, enligt det experimentella protokollet. Denna randomisering är objektiv och deklareras innan experimentet utförs. Den objektiva slumpmässiga tilldelningen används för att testa nollhypotesens signifikans, enligt idéerna från CS Peirce och Ronald Fisher . Denna designbaserade analys diskuterades och utvecklades av Francis J. Anscombe vid Rothamsted Experimental Station och av Oscar Kempthorne vid Iowa State University . Kempthorne och hans elever gör ett antagande om enhetsbehandlingsadditivitet , vilket diskuteras i böckerna av Kempthorne och David R. Cox .

Enhetsbehandlingstillsats

I sin enklaste form anger antagandet om enhetsbehandlingsadditivitet att det observerade svaret $y_{i,j}$ från experimentenhet $i$ vid behandling $j$ kan skrivas som summan av enhetens svar $y_{i}$ och behandlingseffekten $t_{j}$ , dvs.

$$y_{i,j}=y_{i}+t_{j}.$$

Antagandet om enhetsbehandlingsadditivitet innebär att för varje behandling ${\displaystyle j} har$${\displaystyle j}:$ e behandlingen exakt samma effekt $t_{j}$ på varje experimentenhet.

Antagandet om enhetsbehandlingsadditivitet kan vanligtvis inte direkt förfalskas , enligt Cox och Kempthorne. Många konsekvenser av additivitet i behandlingsenheter kan dock förfalskas. För ett randomiserat experiment innebär antagandet om enhetsbehandlingsadditivitet att variansen är konstant för alla behandlingar. Därför, genom kontraposition , är ett nödvändigt villkor för enhetsbehandlingsadditivitet att variansen är konstant.

Användningen av enhetsbehandlingsadditivitet och randomisering liknar den designbaserade slutsatsen som är standard vid undersökningsurval med ändlig population .

Härledd linjär modell

Kempthorne använder randomiseringsfördelningen och antagandet om enhetsbehandlingsadditivitet för att producera en härledd linjär modell, mycket lik läroboksmodellen som diskuterats tidigare. Teststatistiken för denna härledda linjära modell är nära approximerad av teststatistiken för en lämplig normal linjär modell, enligt approximationssatser och simuleringsstudier. Det finns dock skillnader. Till exempel resulterar den randomiseringsbaserade analysen i en liten men (strängt) negativ korrelation mellan observationerna. I den randomiseringsbaserade analysen finns inget antagande om normalfördelning och absolut inget antagande om oberoende . Tvärtom, observationerna är beroende !

Den randomiseringsbaserade analysen har nackdelen att dess exponering involverar tråkig algebra och lång tid. Eftersom den randomiseringsbaserade analysen är komplicerad och nära approximeras av metoden som använder en normal linjär modell, betonar de flesta lärare den normala linjära modellen. Få statistiker protesterar mot modellbaserad analys av balanserade randomiserade experiment.

Statistiska modeller för observationsdata

Men när den tillämpas på data från icke-randomiserade experiment eller observationsstudier saknar modellbaserad analys berättigande till randomisering. För observationsdata måste härledning av konfidensintervall använda subjektiva modeller, vilket betonats av Ronald Fisher och hans anhängare. I praktiken är uppskattningarna av behandlingseffekter från observationsstudier i allmänhet ofta inkonsekventa. I praktiken är "statistiska modeller" och observationsdata användbara för att föreslå hypoteser som bör behandlas mycket försiktigt av allmänheten.

Sammanfattning av antaganden

Se även: Shapiro–Wilk-test , Bartletts test och Levenes test

Den normalmodellbaserade ANOVA-analysen antar oberoendet, normaliteten och homogeniteten hos varianserna hos residualerna. Den randomiseringsbaserade analysen förutsätter endast homogeniteten hos varianserna av resterna (som en konsekvens av enhetsbehandlingsadditivitet) och använder randomiseringsförfarandet för experimentet. Båda dessa analyser kräver homoskedasticitet , som ett antagande för normalmodellanalysen och som en konsekvens av randomisering och additivitet för den randomiseringsbaserade analysen.

Studier av processer som ändrar varianser snarare än medel (kallade spridningseffekter) har dock framgångsrikt genomförts med ANOVA. Det finns inga nödvändiga antaganden för ANOVA i dess fulla allmänhet, men F -testet som används för ANOVA hypotestestning har antaganden och praktiska begränsningar som är av fortsatt intresse.

Problem som inte uppfyller ANOVAs antaganden kan ofta omvandlas till att uppfylla antagandena. Egenskapen för enhetsbehandlingsadditivitet är inte invariant under en "skalförändring", så statistiker använder ofta transformationer för att uppnå enhetsbehandlingsadditivitet. Om svarsvariabeln förväntas följa en parametrisk familj av sannolikhetsfördelningar, kan statistikern specificera (i protokollet för experimentet eller observationsstudien) att svaren transformeras för att stabilisera variansen. En statistiker kan också specificera att logaritmiska transformationer ska tillämpas på svaren, som tros följa en multiplikativ modell. Enligt Cauchys funktionella ekvationssats är logaritmen den enda kontinuerliga transformationen som omvandlar verklig multiplikation till addition.

Egenskaper

ANOVA används i analysen av jämförande experiment, de där endast skillnaden i resultat är av intresse. Experimentets statistiska signifikans bestäms av ett förhållande av två varianser. Detta förhållande är oberoende av flera möjliga förändringar av de experimentella observationerna: Att lägga till en konstant till alla observationer ändrar inte signifikansen. Att multiplicera alla observationer med en konstant ändrar inte signifikansen. Så ANOVAs statistiska signifikansresultat är oberoende av konstant bias och skalningsfel såväl som de enheter som används för att uttrycka observationer. I en tid präglad av mekaniska beräkningar var det vanligt att subtrahera en konstant från alla observationer (när det motsvarar att sjunka inledande siffror) för att förenkla datainmatningen. Detta är ett exempel på datakodning .

Logik

Beräkningarna av ANOVA kan karakteriseras som att man beräknar ett antal medelvärden och varianser, delar två varianser och jämför förhållandet med ett handboksvärde för att bestämma statistisk signifikans. Att beräkna en behandlingseffekt är då trivialt: "effekten av en behandling uppskattas genom att ta skillnaden mellan medelvärdet av de observationer som får behandlingen och det allmänna medelvärdet".

Fördelning av summan av kvadrater

Huvudartikel: Fördelning av summor av kvadrater

Se även: Brist-of-fit summa av kvadrater

ANOVA använder traditionell standardiserad terminologi. Definitionsekvationen för sampelvarians är ${\textstyle s^{2}={\frac {1}{n-1}}\summa _{i }(y_{i}-{\bar {y}})^{2}}$ , där divisorn kallas frihetsgraderna (DF), summan kallas kvadratsumman (SS), resultatet kallas medelkvadraten (MS) och de kvadratiska termerna är avvikelser från provmedelvärdet. ANOVA uppskattar tre urvalsvarianser: en total varians baserat på alla observationsavvikelser från det stora medelvärdet, en felvarians baserat på alla observationsavvikelser från deras lämpliga behandlingsmedel och en behandlingsvarians. Behandlingsvariansen baseras på avvikelserna av behandlingsmedelvärden från det stora medelvärdet, varvid resultatet multipliceras med antalet observationer i varje behandling för att ta hänsyn till skillnaden mellan variansen av observationer och medelvariansen.

Den grundläggande tekniken är en uppdelning av den totala summan av kvadraterna SS i komponenter relaterade till effekterna som används i modellen. Till exempel modellen för en förenklad ANOVA med en typ av behandling på olika nivåer.

$$SS_{\text{Totalt}}=SS_{\text{Fel}}+SS_{\text{Behandlingar}}$$

Antalet frihetsgrader DF kan delas upp på liknande sätt: en av dessa komponenter (det för fel) specificerar en chi-kvadratfördelning som beskriver den associerade summan av kvadrater, medan detsamma gäller för "behandlingar" om det finns ingen behandlingseffekt.

$$DF_{\text{Total}}=DF_{\text{Error}}+DF_{\text{Behandlingar}}$$

F - testet

Huvudartikel: F-test

F - testet används för att jämföra faktorerna för den totala avvikelsen. Till exempel, i envägs- eller enkelfaktor ANOVA, testas statistisk signifikans genom att jämföra F-teststatistiken

$$F={\frac {\text{varians mellan behandlingar}}{\text{varians inom behandlingar}}}$$

$$F={\frac {MS_{\text{Behandlingar}}}{MS_{\ text{Error}}}}={{SS_{\text{Behandlingar}}/(I-1)} \över {SS_{\text{Error}}/(n_{T}-I)}}$$

där MS är medelkvadrat, $I$ är antalet behandlingar och $n_{T}$ är det totala antalet fall

till F -fördelningen med $I-1$ , $n_{T}-I$ frihetsgrader. Att använda F -fördelningen är en naturlig kandidat eftersom teststatistiken är förhållandet mellan två skalade kvadratsummor som var och en följer en skalad chi-kvadratfördelning .

Det förväntade värdet på F är $1+{n\sigma _{\text{Behandling}}^{2}}/{\sigma _{\text{Fel}} ^{2}}$ (där $n$ är behandlingsprovstorleken) vilket är 1 för ingen behandlingseffekt. När F-värdena ökar över 1 blir bevisen allt mer oförenliga med nollhypotesen. Två uppenbara experimentella metoder för att öka F är att öka provstorleken och minska felvariansen genom snäva experimentella kontroller.

Det finns två metoder för att avsluta ANOVA-hypotestestet, som båda ger samma resultat:

• Läroboksmetoden går ut på att jämföra det observerade värdet på F med det kritiska värdet på F bestämt från tabeller. Det kritiska värdet på F är en funktion av täljarens och nämnarens frihetsgrader och signifikansnivån ( α ). Om F ≥ F _Critical , förkastas nollhypotesen.
• Datormetoden beräknar sannolikheten (p-värde) för ett värde på F som är större än eller lika med det observerade värdet. Nollhypotesen förkastas om denna sannolikhet är mindre än eller lika med signifikansnivån ( α ).

ANOVA F -testet är känt för att vara nästan optimalt i betydelsen att minimera falska negativa fel för en fast frekvens av falska positiva fel (dvs. maximera kraften för en fast signifikansnivå). Till exempel, för att testa hypotesen att olika medicinska behandlingar har exakt samma effekt, närmar sig F - testets p -värden nära permutationstestets p-värden : Approximationen är särskilt nära när designen är balanserad. Sådana permutationstester karakteriserar tester med maximal kraft mot alla alternativa hypoteser , som observerats av Rosenbaum. ANOVA F -testet (av nollhypotesen att alla behandlingar har exakt samma effekt) rekommenderas som ett praktiskt test, på grund av dess robusthet mot många alternativa distributioner.

Utökad logik

ANOVA består av separerbara delar; uppdelningskällor för varians och hypotestestning kan användas individuellt. ANOVA används för att stödja andra statistiska verktyg. Regression används först för att anpassa mer komplexa modeller till data, sedan används ANOVA för att jämföra modeller med målet att välja enkla(r) modeller som adekvat beskriver data. "Sådana modeller skulle kunna passa utan någon hänvisning till ANOVA, men ANOVA-verktyg kan sedan användas för att förstå de inpassade modellerna och för att testa hypoteser om partier av koefficienter." "[Vi tänker på variansanalysen som ett sätt att förstå och strukturera flernivåmodeller - inte som ett alternativ till regression utan som ett verktyg för att sammanfatta komplexa högdimensionella slutledningar ..."

För en enda faktor

Huvudartikel: Envägsanalys av varians

Det enklaste experimentet som är lämpligt för ANOVA-analys är det helt randomiserade experimentet med en enda faktor. Mer komplexa experiment med en enda faktor involverar begränsningar för randomisering och inkluderar helt randomiserade block och latinska rutor (och varianter: grekisk-latinska rutor, etc.). De mer komplexa experimenten delar många av komplexiteten hos flera faktorer. En relativt fullständig diskussion av analysen (modeller, datasammanfattningar, ANOVA-tabell) av det helt randomiserade experimentet finns tillgänglig .

Det finns några alternativ till konventionell envägsvariansanalys, t.ex.: Welchs heteroskedastiska F-test, Welchs heteroskedastiska F-test med trimmade medelvärden och Winsorized varianser, Brown-Forsythe-test, Alexander-Govern-test, James andra ordningens test och Kruskal-Wallis-test , tillgänglig i envägstest R

Det är användbart att representera varje datapunkt i följande form, en så kallad statistisk modell:

$$Y_{ij}=\mu +\tau _{j}+\varepsilon _{ij}$$

var

• i = 1, 2, 3, ..., R
• j = 1, 2, 3, ..., C
• μ = totalt genomsnitt (medelvärde)
• τ _j = differentiell effekt (respons) associerad med j- nivån för X; detta antar att värdena för τ _{j totalt sett} adderas till noll (det vill säga ${\textstyle \sum _{j=1}^{C}\tau _{j}=0}$ )
• ε _ij = brus eller fel associerat med det specifika ij- datavärdet

Det vill säga, vi föreställer oss en additiv modell som säger att varje datapunkt kan representeras genom att summera tre kvantiteter: det sanna medelvärdet, medelvärde över alla faktornivåer som undersöks, plus en inkrementell komponent associerad med den specifika kolumnen (faktornivå), plus en slutlig komponent associerad med allt annat som påverkar det specifika datavärdet.

För flera faktorer

Huvudartikel: Tvåvägsanalys av varians

ANOVA generaliserar till studiet av effekterna av flera faktorer. När experimentet inkluderar observationer vid alla kombinationer av nivåer av varje faktor kallas det för faktoriell . Faktoriella experiment är mer effektiva än en serie enfaktorexperiment och effektiviteten ökar när antalet faktorer ökar. Följaktligen används fabriksdesigner flitigt.

Användningen av ANOVA för att studera effekterna av flera faktorer har en komplikation. I en 3-vägs ANOVA med faktorerna x, y och z innehåller ANOVA-modellen termer för huvudeffekterna (x, y, z) och termer för interaktioner (xy, xz , yz, xyz). Alla termer kräver hypotestest. Spridningen av interaktionstermer ökar risken för att något hypotestest kommer att ge ett falskt positivt av en slump. Lyckligtvis säger erfarenheten att interaktioner av hög ordning är sällsynta. Möjligheten att upptäcka interaktioner är en stor fördel med multipelfaktor ANOVA. Att testa en faktor i taget döljer interaktioner, men ger uppenbarligen inkonsekventa experimentella resultat.

Försiktighet rekommenderas vid interaktioner; Testa interaktionstermer först och utöka analysen bortom ANOVA om interaktioner hittas. Texter varierar i sina rekommendationer angående fortsättningen av ANOVA-proceduren efter att ha stött på en interaktion. Interaktioner komplicerar tolkningen av experimentella data. Varken beräkningarna av signifikans eller de uppskattade behandlingseffekterna kan tas till nominellt värde. "En betydande interaktion kommer ofta att maskera betydelsen av huvudeffekter." Grafiska metoder rekommenderas för att öka förståelsen. Regression är ofta användbart. En lång diskussion om interaktioner finns tillgänglig i Cox (1958). Vissa interaktioner kan tas bort (genom transformationer) medan andra inte kan.

En mängd olika tekniker används med multipelfaktor ANOVA för att minska kostnaderna. En teknik som används i faktoriell design är att minimera replikering (möjligen ingen replikering med stöd av analytiska knep ) och att kombinera grupper när effekter befinns vara statistiskt (eller praktiskt taget) obetydliga. Ett experiment med många obetydliga faktorer kan kollapsa till ett med ett fåtal faktorer som stöds av många replikationer.

Tillhörande analys

Vissa analyser krävs för att stödja experimentets design medan andra analyser utförs efter att förändringar i faktorerna formellt visat sig ge statistiskt signifikanta förändringar i svaren. Eftersom experiment är iterativt ändrar resultaten av ett experiment planerna för följande experiment.

Förberedande analys

Antalet experimentella enheter

Vid utformningen av ett experiment planeras antalet experimentella enheter för att tillfredsställa försökets mål. Experiment är ofta sekventiellt.

Tidiga experiment är ofta utformade för att ge genomsnittliga opartiska uppskattningar av behandlingseffekter och experimentella fel. Senare experiment är ofta utformade för att testa en hypotes om att en behandlingseffekt har en viktig storlek; i detta fall väljs antalet experimentella enheter så att experimentet ligger inom budget och har tillräcklig kraft, bland annat.

Rapportering av provstorleksanalys krävs i allmänhet inom psykologi. "Ge information om urvalsstorlek och processen som ledde till beslut om urvalsstorlek." Analysen, som skrivs i försöksprotokollet innan försöket genomförs, prövas i anslagsansökningar och administrativa prövningsnämnder.

Förutom effektanalysen finns det mindre formella metoder för att välja antalet experimentella enheter. Dessa inkluderar grafiska metoder baserade på att begränsa sannolikheten för falska negativa fel, grafiska metoder baserade på en förväntad variationsökning (över residualerna) och metoder baserade på att uppnå ett önskat konfidensintervall.

Effektanalys

Effektanalys används ofta i ANOVA-sammanhang för att bedöma sannolikheten för att framgångsrikt förkasta nollhypotesen om vi antar en viss ANOVA-design, effektstorlek i populationen, urvalsstorlek och signifikansnivå. Effektanalys kan hjälpa till med studiedesign genom att bestämma vilken urvalsstorlek som skulle krävas för att ha en rimlig chans att förkasta nollhypotesen när den alternativa hypotesen är sann.

Effektstorlek

Effektstorlek

Huvudartikel: Effektstorlek

Flera standardiserade effektmått har föreslagits för ANOVA för att sammanfatta styrkan i sambandet mellan en eller flera prediktorer och den beroende variabeln eller den övergripande standardiserade skillnaden för den kompletta modellen. Standardiserade uppskattningar av effektstorlek underlättar jämförelse av resultat mellan studier och discipliner. Men medan standardiserade effektstorlekar ofta används i mycket av den professionella litteraturen, kan ett icke-standardiserat mått på effektstorlek som har omedelbart "meningsfulla" enheter vara att föredra för rapporteringsändamål.

Modellbekräftelse

Ibland utförs tester för att avgöra om antagandena för ANOVA verkar vara kränkta. Rester undersöks eller analyseras för att bekräfta homoskedasticitet och grov normalitet. Rester bör ha utseendet av (noll genomsnittlig normalfördelning) brus när de plottas som en funktion av allt inklusive tid och modellerade datavärden. Trender antyder interaktioner mellan faktorer eller mellan observationer.

Uppföljande tester

En statistiskt signifikant effekt i ANOVA följs ofta av ytterligare tester. Detta kan göras för att bedöma vilka grupper som skiljer sig från vilka andra grupper eller för att testa olika andra fokuserade hypoteser. Uppföljningstester särskiljs ofta i termer av om de är "planerade" ( a priori ) eller "post hoc ". Planerade tester bestäms innan man tittar på data, och post hoc-tester skapas först efter man tittar på data (även om termen "post hoc" används inkonsekvent).

Uppföljningstesterna kan vara "enkla" parvisa jämförelser av individuella gruppmedelvärden eller kan vara "sammansatta" jämförelser (t.ex. jämföra medelvärdet för sammanslagningen mellan grupperna A, B och C med medelvärdet för grupp D). Jämförelser kan också titta på trendtester, såsom linjära och kvadratiska samband, när den oberoende variabeln involverar ordnade nivåer. Ofta innehåller uppföljningstesterna en metod för att justera för problemet med flera jämförelser .

Uppföljningstester för att identifiera vilka specifika grupper, variabler eller faktorer som har statistiskt olika medel inkluderar Tukey's range-test och Duncans nya multiple range-test . Dessa tester följs i sin tur ofta med en Compact Letter Display (CLD) metodik för att göra resultatet av de nämnda testerna mer transparent för en icke-statistiker publik.

Studiedesigner

Det finns flera typer av ANOVA. Många statistiker baserar ANOVA på experimentets design , särskilt på protokollet som specificerar slumpmässig tilldelning av behandlingar till försökspersoner; protokollets beskrivning av tilldelningsmekanismen bör innehålla en specifikation av behandlingarnas struktur och eventuell blockering . Det är också vanligt att tillämpa ANOVA på observationsdata med hjälp av en lämplig statistisk modell.

Vissa populära mönster använder följande typer av ANOVA:

• Envägs ANOVA används för att testa för skillnader mellan två eller flera oberoende grupper (medel), t.ex. olika nivåer av ureaapplicering i en gröda, eller olika nivåer av antibiotikaverkan på flera olika bakteriearter, eller olika nivåer av effekt av något läkemedel på patientgrupper. Men om dessa grupper inte är oberoende, och det finns en ordning i grupperna (såsom mild, måttlig och svår sjukdom), eller i dosen av ett läkemedel (såsom 5 mg/ml, 10 mg/ml, 20 mg /ml) ges till samma patientgrupp, bör en linjär trenduppskattning användas. Vanligtvis används dock envägs ANOVA för att testa för skillnader mellan minst tre grupper, eftersom tvågruppsfallet kan täckas av ett t-test . När det bara finns två sätt att jämföra är t-testet och ANOVA F -testet ekvivalenta; relationen mellan ANOVA och t ges av F = t ² .
• Faktoriell ANOVA används när det finns mer än en faktor.
• Upprepade åtgärder ANOVA används när samma försökspersoner används för varje faktor (t.ex. i en longitudinell studie ).
• Multivariat variansanalys (MANOVA) används när det finns mer än en svarsvariabel .

Varningar

Balanserade experiment (de med samma provstorlek för varje behandling) är relativt lätta att tolka; obalanserade experiment ger mer komplexitet. För enkelfaktors (envägs) ANOVA är justeringen för obalanserad data enkel, men den obalanserade analysen saknar både robusthet och kraft. För mer komplexa konstruktioner leder bristen på balans till ytterligare komplikationer. "Ortogonalitetsegenskapen för huvudeffekter och interaktioner som finns i balanserade data överförs inte till det obalanserade fallet. Detta betyder att den vanliga analysen av varianstekniker inte gäller. Följaktligen är analysen av obalanserade faktorialer mycket svårare än den för balanserade faktorer. mönster." I det allmänna fallet "kan variansanalysen också tillämpas på obalanserade data, men då kommer summan av kvadrater, medelkvadrater och F -kvoter att bero på i vilken ordning variationskällorna beaktas."

ANOVA är (delvis) ett test av statistisk signifikans. American Psychological Association (och många andra organisationer) anser att det är otillräckligt att bara rapportera statistisk signifikans och att rapportering av förtroendegränser är att föredra.

Generaliseringar

ANOVA anses vara ett specialfall av linjär regression som i sin tur är ett specialfall av den allmänna linjära modellen . Alla anser att observationerna är summan av en modell (passning) och en rest (fel) som ska minimeras.

Kruskal –Wallis-testet och Friedman-testet är icke-parametriska test, som inte förlitar sig på ett antagande om normalitet.

Anslutning till linjär regression

Nedan klargör vi sambandet mellan multi-way ANOVA och linjär regression.

Ordna om data linjärt så att ${\displaystyle k} -th$$Z_{k,b}$ associeras med ett svar $y_{k}$ och faktorerna där $b\in \{1,2,\ldots ,B\}$ anger de olika faktorerna och $B$ är det totala antalet faktorer. I envägs ANOVA $B=1$ och i tvåvägs ANOVA $B=2$ . Dessutom antar vi att $b$ -th faktorn har $I_{b}$ nivåer, nämligen $\{1,2,\ldots , I_{b}\}$ . Nu kan vi en-hot- koda faktorerna till ${\textstyle \sum _{b=1}^{B}I_{b}}$ dimensionell vektor $v_{k}$ .

One-hot-kodningsfunktionen $g_{b}:\{1,2,\ldots ,I_{b}\}\ mapsto \{0,1\}^{I_{b}}$ definieras så att $i$ -th posten av $g_{b}(Z_{k ,b})$ är

$$g_{b}(Z_{k,b})_{i}={\begin{cases}1&{\text {if }}i=Z_{k,b}\\0&{\text{annars}}\end{case}}$$

Vektorn $v_{k}$ är sammanlänkningen av alla ovanstående vektorer för alla $b$ . Således, $v_{k}=[g_{1}(Z_ {k,1}),g_{2}(Z_{k,2}),\ldots ,g_{B}(Z_{k,B})]$ . För att erhålla en helt generell $B$ -vägsinteraktion ANOVA måste vi också sammanfoga varje ytterligare interaktionsterm i vektorn $v_{k}$ och sedan lägga till en interceptterm. Låt den vektorn vara $X_{k}$ .

Med denna notation på plats har vi nu det exakta sambandet med linjär regression. Vi regresserar helt enkelt svaret $y_{k}$ mot vektorn $X_{k}$ . Det finns dock en oro för identifierbarhet . För att övervinna sådana problem antar vi att summan av parametrarna inom varje uppsättning interaktioner är lika med noll. Härifrån kan man använda F -statistik eller andra metoder för att bestämma relevansen av de enskilda faktorerna.

Exempel

Vi kan betrakta exemplet med 2-vägsinteraktion där vi antar att den första faktorn har 2 nivåer och den andra faktorn har 3 nivåer.

Definiera $a_{i}=1$ om $Z_{k,1}=i$ och $b_{i}=1$ om $Z_{k,2}=i$ , dvs $a$ är one-hot-kodningen av den första faktorn och $b$ är en-hot-kodningen av den andra faktorn.

Med det,

$$X_{k}=[a_{1},a_{2},b_{1},b_{2},b_{3},a_{1}\ gånger b_{1 },a_{1}\ gånger b_{2},a_{1}\ gånger b_{3},a_{2}\ gånger b_{1},a_{2}\ gånger b_{2},a_{2} \times b_{3},1]$$

där den sista termen är en interceptterm. För ett mer konkret exempel anta det

$${\begin{aligned}Z_{k,1}&=2\\Z_{k,2}&=1\end{aligned}}$$

Sedan,

$$X_{k}=[0,1,1,0,0,0,0,0,1,0,0 ,1]$$

Se även

• ANOVA i leden
• ANOVA-samtidig komponentanalys
• Analys av kovarians ( ANCOVA )
• Analys av molekylär varians (AMOVA)
• Analys av rytmisk varians (ANORVA)
• Förväntade medelvärden
• Förklarad variation
• Linjär trenduppskattning
• Variansanalys med blandad design
• Multivariat analys av kovarians ( MANCOVA )
• Permutationsanalys av varians
• Variansupplösning

Anteckningar

•    Anscombe, FJ (1948). "Giltigheten av jämförande experiment". Journal of the Royal Statistical Society. Serie A (Allmänt) . 111 (3): 181–211. doi : 10.2307/2984159 . JSTOR 2984159 . MR 0030181 .
•   Bailey, RA (2008). Utformning av jämförande experiment . Cambridge University Press. ISBN 978-0-521-68357-9 . Förpubliceringskapitel finns tillgängliga online.
•   Belle, Gerald van (2008). Statistiska tumregler (2:a uppl.). Hoboken, NJ: Wiley. ISBN 978-0-470-14448-0 .
•   Cochran, William G.; Cox, Gertrude M. (1992). Experimentell design (2:a upplagan). New York: Wiley. ISBN 978-0-471-54567-5 .
•   Cohen, Jacob (1988). Statistisk maktanalys för beteendevetenskaperna (2:a uppl.). Routledge ISBN 978-0-8058-0283-2
•   Cohen, Jacob (1992). "Statistik en kraftprimer". Psykologisk Bulletin . 112 (1): 155–159. doi : 10.1037/0033-2909.112.1.155 . PMID 19565683 .
•   Cox, David R. (1958). Planering av experiment . Omtryckt som ISBN 978-0-471-57429-3
•   Cox, David R. (2006). Principer för statistisk slutledning . Cambridge New York: Cambridge University Press. ISBN 978-0-521-68567-2 .
•   Freedman, David A. (2005). Statistiska modeller: teori och praktik , Cambridge University Press. ISBN 978-0-521-67105-7
•   Gelman, Andrew (2005). "Variansanalys? Varför är det viktigare än någonsin". Statistikens annaler . 33 : 1–53. arXiv : math/0504499 . doi : 10.1214/009053604000001048 . S2CID 13529149 .
•   Gelman, Andrew (2008). "Varians, analys av". Den nya Palgrave dictionary of economics (2:a upplagan). Basingstoke, Hampshire New York: Palgrave Macmillan. ISBN 978-0-333-78676-5 .
•   Hinkelmann, Klaus & Kempthorne, Oscar (2008). Design och analys av experiment . Vol. I och II (andra upplagan). Wiley. ISBN 978-0-470-38551-7 .
•   Howell, David C. (2002). Statistiska metoder för psykologi (5:e uppl.). Pacific Grove, CA: Duxbury/Thomson Learning. ISBN 978-0-534-37770-0 .
•   Kempthorne, Oscar (1979). The Design and Analysis of Experiments (Rättad nytryck av (1952) Wiley ed.). Robert E. Krieger. ISBN 978-0-88275-105-4 .
• Lehmann, EL (1959) Testa statistiska hypoteser. John Wiley & Sons.
•   Montgomery, Douglas C. (2001). Design och analys av experiment (5:e upplagan). New York: Wiley. ISBN 978-0-471-31649-7 .
•   Moore, David S. & McCabe, George P. (2003). Introduktion till praktiken av statistik (4e). WH Freeman & Co. ISBN 0-7167-9657-0
•   Rosenbaum, Paul R. (2002). Observationsstudier (2:a uppl.). New York: Springer-Verlag. ISBN 978-0-387-98967-9
• Scheffé, Henry (1959). Variansanalysen . New York: Wiley.
•   Stigler, Stephen M. (1986). Statistikens historia: mätningen av osäkerhet före 1900 . Cambridge, Mass: Belknap Press vid Harvard University Press. ISBN 978-0-674-40340-6 .
•    Wilkinson, Leland (1999). "Statistiska metoder i psykologitidskrifter; riktlinjer och förklaringar". Amerikansk psykolog . 5 (8): 594–604. CiteSeerX 10.1.1.120.4818 . doi : 10.1037/0003-066X.54.8.594 . S2CID 428023 .

Vidare läsning

•   Box, G. ep (1953). "Icke-normalitet och tester på avvikelser". Biometrika . 40 (3/4): 318–335. doi : 10.1093/biomet/40.3-4.318 . JSTOR 2333350 .
• Box, GEP (1954). "Några satser om kvadratiska former som tillämpas i studien av analys av variansproblem, I. Effekten av variansolikhet i envägsklassificeringen" . The Annals of Mathematical Statistics . 25 (2): 290. doi : 10.1214/aoms/1177728786 .
• Box, GEP (1954). "Några satser om kvadratiska former som tillämpas i studien av analys av variansproblem, II. Effekter av ojämlikhet i varians och av korrelation mellan fel i tvåvägsklassificeringen" . The Annals of Mathematical Statistics . 25 (3): 484. doi : 10.1214/aoms/1177728717 .
•   Caliński, Tadeusz; Kageyama, Sanpei (2000). Blockdesigner: A Randomization approach, Volym I : Analys . Föreläsningsanteckningar i statistik. Vol. 150. New York: Springer-Verlag. ISBN 978-0-387-98578-7 .
•   Christensen, Ronald (2002). Plane Answers to Complex Questions: Theory of Linear Models (tredje upplagan). New York: Springer. ISBN 978-0-387-95361-8 .
•   Cox, David R. & Reid, Nancy M. (2000). Teorin för design av experiment . (Chapman & Hall/CRC). ISBN 978-1-58488-195-7
•   Fisher, Ronald (1918). "Studies in Crop Variation. I. En undersökning av skörden av säd från Broadbalk" ( PDF) . Journal of Agricultural Science . 11 (2): 107–135. doi : 10.1017/S0021859600003750 . hdl : 2440/15170 . S2CID 86029217 . Arkiverad från originalet (PDF) den 12 juni 2001.
•   Freedman, David A. ; Pisani, Robert; Purves, Roger (2007) Statistics , 4:e upplagan. WW Norton & Company ISBN 978-0-393-92972-0
•    Hettmansperger, TP; McKean, JW (1998). Edward Arnold (red.). Robusta icke-parametriska statistiska metoder . Kendall's Library of Statistics. Vol. 5 (första upplagan). New York: John Wiley & Sons, Inc. s. xiv+467 s. ISBN 978-0-340-54937-7 . MR 1604954 .
•   Lentner, Marvin; Thomas Bishop (1993). Experimentell design och analys (andra upplagan). Blacksburg, VA: Valley Book Company. ISBN 978-0-9616255-2-8 .
•   Tabachnick, Barbara G. & Fidell, Linda S. (2007). Använda multivariat statistik (5:e upplagan). Boston: Pearson International Edition. ISBN 978-0-205-45938-4
•    Wichura, Michael J. (2006). Den koordinatfria inställningen till linjära modeller . Cambridge-serien i statistisk och probabilistisk matematik. Cambridge: Cambridge University Press. s. xiv+199. ISBN 978-0-521-86842-6 . MR 2283455 .
•   Phadke, Madhav S. (1989). Kvalitetsteknik med robust design . New Jersey: Prentice Hall PTR. ISBN 978-0-13-745167-8 .

externa länkar

• SOCR : ANOVA-aktivitet
• Exempel på alla ANOVA- och ANCOVA-modeller med upp till tre behandlingsfaktorer, inklusive randomiserat block, delad plot, upprepade mätningar och latinska rutor, och deras analys i R ( University of Southampton)
• NIST/SEMATECH e-Handbook of Statistical Methods, avsnitt 7.4.3: "Är medelvärdet lika?"
• Variansanalys: Introduktion