Monotone sannolikhetsförhållande

Ett monotont sannolikhetsförhållande i fördelningarna $f(x)$ och $g(x)$

Förhållandet mellan densitetsfunktionerna ovan ökar i parametern $x$ , så $f(x)/g(x)$ uppfyller egenskapen monoton likelihood ratio .

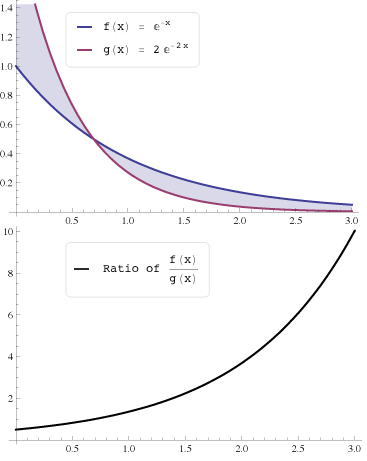
I statistik är den monotona sannolikhetsförhållandeegenskapen en egenskap hos förhållandet mellan två sannolikhetstäthetsfunktioner ( PDF). Formellt bär fördelningarna ƒ ( x ) och g ( x ) egenskapen if

${\text{för varje }}x_{1}>x_{0},\quad { \frac {f(x_{1})}{g(x_{1})}}\geq {\frac {f(x_{0})}{g(x_{0})}}$

det vill säga om förhållandet är icke-minskande i argumentet $x$ .

Om funktionerna är först-differentierbara kan egenskapen ibland anges

${\frac {\partial }{\partial x}}\left({\frac {f(x)}{g(x)}}\ höger)\geq 0$

För två distributioner som uppfyller definitionen med avseende på något argument x, säger vi att de "har MLRP i x ." För en familj av distributioner som alla uppfyller definitionen med avseende på viss statistik T ( X ), säger vi att de "har MLR i T ( X )."

Intuition

MLRP används för att representera en datagenererande process som har ett enkelt förhållande mellan storleken på en observerad variabel och fördelningen den hämtar från. Om $f(x)$ uppfyller MLRP med avseende på $g(x)$ , ju högre det observerade värdet ${\displaystyle x} är$ , desto mer sannolikt att det ritades från distributionen $f$ istället för $g$ . Som vanligt för monotona relationer kommer sannolikhetsförhållandets monotonitet till nytta i statistik, särskilt när man använder uppskattning av maximal sannolikhet . Distributionsfamiljer med MLR har också ett antal väluppfostrade stokastiska egenskaper, såsom första ordningens stokastisk dominans och ökande riskkvoter . Tyvärr, som också är vanligt, kommer styrkan i detta antagande till priset av realism. Många processer i världen uppvisar inte en monoton överensstämmelse mellan input och output.

Exempel: Arbetar hårt eller slappar av

Anta att du arbetar med ett projekt, och du kan antingen arbeta hårt eller slappa av. Kalla ditt val av insats $e$ och kvaliteten på det resulterande projektet $q$ . Om MLRP gäller för distributionen av q beroende på din ansträngning $e$ , desto högre kvalitet desto mer sannolikt att du arbetade hårt. Omvänt, ju lägre kvalitet desto mer sannolikt att du slappnade av.

1. Välj ansträngning $e\in \{H,L\}$ där H betyder hög, L betyder låg
2. Observera $q$ ritad från $f(q\mid e)$ . Enligt Bayes lag med en enhetlig prior,

   $\Pr[e=H\mid q] ={\frac {f(q\midt H)}{f(q\midt H)+f(q\midt L)}}$

3. Antag att $f(q\mid e)$ uppfyller MLRP. Omarrangeras, är sannolikheten att arbetaren arbetat hårt

${\frac {1}{1+f(q\mid L)/f(q\mid H)}}$

som tack vare MLRP, ökar monotont i $q$ (eftersom $f(q\mid L)/f(q\mid H)$ minskar i $q$ ). Om någon arbetsgivare gör en "prestationsgranskning" kan han alltså sluta sig till sin anställdes beteende utifrån fördelarna med hans arbete.

Familjer av distributioner som uppfyller MLR

Statistiska modeller antar ofta att data genereras av en distribution från någon familj av distributioner och försöker bestämma den fördelningen. Denna uppgift förenklas om familjen har egenskapen monotone likelihood ratio (MLRP).

En familj av densitetsfunktioner $\{f_{\theta }(x)\}_{\theta \in \Theta }$ indexerad av en parameter $\theta$ tar värden i en ordnad uppsättning $\Theta$ sägs ha en monoton likelihood ratio (MLR) i statistiken $T(X)$ om för någon ${\ displaystyle \theta _{1}<\theta _{2}}$ ,

${\frac {f_{\theta _{2}} (X=x_{1},x_{2},x_{3},\dots )}{f_{\theta _{1}}(X=x_{1},x_{2},x_{3}, \dots )}}$ är en icke-minskande funktion av $T(X)$ .

Sedan säger vi att familjen av distributioner "har MLR i $T(X)$ ".

Lista över familjer

Familj	$T(X)$ där $f_{\theta }(X)$ har MLR
Exponentiell $[\lambda ]$	$\sum x_{i}$ observationer
Binomial $[n,p]$	$\sum x_{i}$ observationer
Poisson $[\lambda ]$	$\sum x_{i}$ observationer
Normal $[\mu ,\sigma ]$	om $\sigma$ känd, $\sum x_{i}$ observationer

Hypotestestning

Om familjen av slumpvariabler har MLRP i $T(X)$ , kan ett enhetligt mest kraftfull test enkelt bestämmas för hypotesen $H_{0}:\theta \leq \theta _{0}$ kontra $H_{1}:\theta >\theta _{0}$ .

Exempel: Ansträngning och resultat

Exempel: Låt $e$ vara en input till en stokastisk teknik – till exempel arbetarens ansträngning – och $y$ dess utdata, vars sannolikhet beskrivs av en sannolikhetstäthetsfunktion $f(y;e).$ Sedan uttrycks den monotona sannolikhetsförhållandeegenskapen (MLRP) för familjen $f$ på följande sätt: för valfri $e_{1},e_ {2}$ , det faktum att $e_{2}>e_{1}$ antyder att förhållandet $f( y;e_{2})/f(y;e_{1})$ ökar i $y$ .

Relation till andra statistiska egenskaper

Monotona sannolikheter används inom flera områden av statistisk teori, inklusive punktuppskattning och hypotestestning , såväl som i sannolikhetsmodeller .

Exponentiella familjer

Enparameters exponentiella familjer har monotona sannolikhetsfunktioner. I synnerhet den endimensionella exponentiella familjen av sannolikhetstäthetsfunktioner eller sannolikhetsmassfunktioner med

$f_{\theta }(x)=c(\theta )h(x)\exp( \pi (\theta )T(x))$

har ett monotont icke-minskande sannolikhetsförhållande i den tillräckliga statistiken T ( x ), förutsatt att $\pi (\theta )$ är icke-minskande.

Uniformt mest kraftfulla tester: Karlin–Rubin-satsen

Monotona sannolikhetsfunktioner används för att konstruera de mest kraftfulla testerna på ett enhetligt sätt , enligt Karlin-Rubin-satsen . Betrakta en skalär mätning som har en sannolikhetstäthetsfunktion parametriserad av en skalär parameter θ , och definiera sannolikhetsförhållandet $\ell (x)=f_{\ theta _{1}}(x)/f_{\theta _{0}}(x)$ . Om $\ell (x)$ är monoton icke-minskande, i ${\displaystyle x} ,$ för valfritt par $\theta _{1}\geq \theta _{ 0}$ (vilket betyder att ju större $x$ är, desto mer sannolikt är $H_{1}$ ), då är tröskeltestet:

$\varphi (x)={\begin{cases}1&{\text{if }}x>x_{0}\\0&{\text {if }}x<x_{0}\end{cases}}$

där $x_{0}$ är vald så att $\operatorname {E} _{ \theta _{0}}\varphi (X)=\alpha$

är UMP-testet av storlek α för att testa $H_{0}:\theta \leq \theta _{0}{\text{ vs. }}H_{1}:\theta >\theta _{0}.$

Observera att exakt samma test också är UMP för att testa $H_{0}:\theta =\theta _{0}{\text{ vs. }}H_{1}:\theta >\theta _{0}.$

Median opartisk uppskattning

Monotona sannolikhetsfunktioner används för att konstruera median-opartiska estimatorer , med hjälp av metoder specificerade av Johann Pfanzagl och andra. En sådan procedur är en analog till Rao–Blackwell -proceduren för medel-opartiska skattningar : Proceduren gäller för en mindre klass av sannolikhetsfördelningar än Rao–Blackwell-proceduren för medel-opartisk uppskattning men för en större klass av förlustfunktioner .

Livstidsanalys: Överlevnadsanalys och tillförlitlighet

Om en familj av distributioner $f_{\theta }(x)$ har egenskapen monoton likelihood ratio i $T(X)$ ,

1. familjen har monotont minskande riskfrekvens i $\theta$ (men inte nödvändigtvis i $T(X)$ )
2. familjen uppvisar den första ordningens (och därmed andra ordningens) stokastiska dominansen i $x$ , och den bästa Bayesianska uppdateringen av $\theta$ ökar i $T(X )$ .

Men inte omvänt: varken monotona riskfrekvenser eller stokastisk dominans innebär MLRP.

Bevis

Låt distributionsfamiljen $f_{\theta }$ uppfylla MLR i x , så att för $\theta _{1}>\theta _{0}$ och ${\ displaystyle x_{1}>x_{0}}$ :

${\frac {f_{\theta _{1}}(x_{1})}{ f_{\theta _{0}}(x_{1})}}\geq {\frac {f_{\theta _{1}}(x_{0})}{f_{\theta _{0}}( x_{0})}},$

eller motsvarande:

$f_{\theta _{1}}(x_{1})f_{\theta _{0}}(x_{0})\geq f_{\theta _{1}}(x_{0}) f_{\theta _{0}}(x_{1}).\,$

Genom att integrera detta uttryck två gånger får vi:

1. Till $x_{1}$ med avseende på $x_{0}$ ${\begin{aligned}&\int _{\min _{x}\in X}^{x_{1}}f_ {\theta _{1}}(x_{1})f_{\theta _{0}}(x_{0})\,dx_{0}\\[6pt]\geq {}&\int _{\ min _{x}\in X}^{x_{1}}f_{\theta _{1}}(x_{0})f_{\theta _{0}}(x_{1})\,dx_{ 0}\end{aligned}}$ integrera och ordna om för att erhålla ${\frac {f_{\theta _{1}}}{f_{\theta _{0}}}}(x)\ geq {\frac {F_{\theta _{1}}}{F_{\theta _{0}}}}(x)$		2. Från $x_{0}$ med avseende på $x_{1}$ ${\begin{aligned}&\int _{x_{0}}^{\max _{x}\in X}f_ {\theta _{1}}(x_{1})f_{\theta _{0}}(x_{0})\,dx_{1}\\[6pt]\geq {}&\int _{x_ {0}}^{\max _{x}\in X}f_{\theta _{1}}(x_{0})f_{\theta _{0}}(x_{1})\,dx_{ 1}\end{aligned}}$ integrera och ordna om för att erhålla ${\frac {1-F_{\theta _{1}}(x)}{1-F_ {\theta _{0}}(x)}}\geq {\frac {f_{\theta _{1}}}{f_{\theta _{0}}}}(x)$

Första ordningens stokastisk dominans

Kombinera de två ojämlikheterna ovan för att få första ordningens dominans:

$F_{\theta _{1}}(x)\leq F_{\theta _{0}}(x)\ \forall x$

Monotone riskfrekvens

Använd endast den andra olikheten ovan för att få en monoton riskfrekvens:

${\frac {f_{\theta _{1}}(x)}{ 1-F_{\theta _{1}}(x)}}\leq {\frac {f_{\theta _{0}}(x)}{1-F_{\theta _{0}}(x) }}\ \forall x$

Används

Ekonomi

MLR är ett viktigt villkor för typfördelningen av agenter i mekanismdesign och informationsekonomi , där Paul Milgrom definierade "favorableness" av signaler (i termer av stokastisk dominans) som en konsekvens av MLR. De flesta lösningar på mekanismdesignmodeller antar typfördelningar som uppfyller MLR för att dra fördel av lösningsmetoder som kan vara lättare att tillämpa och tolka.