Strukturell ekvationsmodellering

För tidskriften, se Strukturell ekvationsmodellering (journal) .
An example structural equation model
Figur 1. Ett exempel på en strukturell ekvationsmodell efter skattning. Latenta variabler anges normalt med ovaler och observerade variabler visas i rektanglar. Rester och varianser ritas som dubbelhåriga pilar (visas här) eller enkla pilar och en cirkel (används inte här). Den latenta IQ-variansen är fixerad till 1 för att ge modellen skala. Figur 1 visar mätfel som påverkar varje indikator på latent intelligens och varje indikator på latent prestation. Varken indikatorerna eller mätfelen för indikatorerna modelleras som att de påverkar de latenta variablerna, men de skulle kunna göra det om forskaren valde att modellera dem.
An example structural equation model pre-estimation
Figur 2. Ett exempel på en strukturell ekvationsmodell före skattning. Liknar figur 1 men utan standardiserade värden och färre poster. Eftersom intelligens och akademisk prestation bara är inbillade eller teoripostulerade variabler, är deras exakta skalvärden okända, även om modellen specificerar att varje latent variabels värden måste falla någonstans längs den observerbara skalan som en av indikatorerna besitter. 1.0-effekten som kopplar en latent till en indikator anger att varje verklig enhetsökning eller minskning av den latenta variabelns värde resulterar i en motsvarande enhetsökning eller minskning av indikatorns värde. Förhoppningen är att en bra indikator har valts för varje latent, men 1,0-värdena signalerar inte perfekt mätning eftersom denna modell också postulerar att det finns andra ospecificerade enheter som orsakar de observerade indikatormätningarna, och därigenom introducerar mätfel. Denna modell postulerar att separata mätfel påverkar var och en av de två indikatorerna på latent intelligens och varje indikator på latent prestation. Den omärkta pilen som pekar på akademisk prestation erkänner att andra saker än intelligens också kan påverka akademiska prestationer.

Strukturell ekvationsmodellering ( SEM ) är en etikett för en mångsidig uppsättning metoder som används av forskare i både experimentell och observationsforskning inom vetenskap, näringsliv och andra områden. Det används mest inom samhälls- och beteendevetenskap.

SEM involverar konstruktionen av en modell , för att representera hur olika aspekter av ett observerbart eller teoretiskt fenomen anses vara kausalt strukturellt relaterade till varandra. Den strukturella aspekten av modellen innebär teoretiska samband mellan variabler som representerar det fenomen som undersöks. Den postulerade kausala struktureringen avbildas ofta med pilar som representerar kausala samband mellan variabler (som i figurerna 1 och 2) men dessa orsakssamband kan representeras på samma sätt som ekvationer. De kausala strukturerna innebär att specifika sambandsmönster bör förekomma bland variablernas värden, och de observerade sambanden mellan variablernas värden används för att uppskatta storleken på orsakseffekterna, och för att testa om de observerade uppgifterna överensstämmer med eller inte. den postulerade kausala struktureringen. Ekvationerna i SEM är matematiska och statistiska egenskaper som antyds av modellen och dess strukturella egenskaper, och sedan uppskattas med statistiska algoritmer (vanligtvis baserade på matrisalgebra och generaliserade linjära modeller ) som körs på experimentella eller observationsdata.

Gränsen mellan vad som är och inte är en strukturell ekvationsmodell är inte alltid tydlig, men SE-modeller innehåller ofta postulerade kausala samband mellan en uppsättning latenta variabler (variabler som tros existera men som inte kan observeras direkt) och kausala samband som länkar de postulerade variablerna. latenta variabler till variabler som kan observeras och vars värden är tillgängliga i någon datauppsättning. Variationer mellan stilarna för latenta orsakssamband, variationer mellan de observerade variablerna som mäter de latenta variablerna och variationer i de statistiska uppskattningsstrategierna resulterar i SEM-verktygssatsen inklusive bekräftande faktoranalys , bekräftande sammansatt analys , väganalys , multigruppsmodellering, longitudinell modellering , partiell minsta kvadraters vägmodellering , latent tillväxtmodellering och hierarkisk eller flernivåmodellering.

Användning av SEM är ofta motiverat eftersom det hjälper till att identifiera latenta variabler som tros existera, men som inte kan observeras direkt (som en attityd, intelligens eller psykisk sjukdom). Även om det inte alltid finns tydliga gränser för vad som är och vad som inte är SEM, handlar det i allmänhet om vägmodeller (se även väganalys ) och mätmodeller (se även faktoranalys ) och använder alltid statistiska modeller och datorprogram för att undersöka de strukturella sambanden mellan latenta variabler som ligger till grund för de faktiska variablerna hämtade från observerade data. Forskare som använder SEM använder program för att uppskatta styrkan och tecknet på en koefficient för varje modellerad pil (siffrorna som visas i figur 1 till exempel), och för att ge diagnostiska ledtrådar som föreslår vilka indikatorer eller modellkomponenter som kan ge inkonsekvens mellan modellen och data . Kritik av SEM-metoder antyder matematiska formuleringsproblem, en tendens att acceptera modeller utan att etablera extern validitet och potentiell filosofisk fördom.

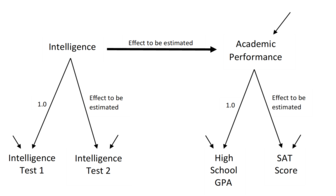
En SEM som tyder på att intelligens (mätt med fyra frågor) kan förutsäga akademisk prestation (mätt med SAT, ACT och high school GPA) visas i figur 1. Begreppet mänsklig intelligens kan inte mätas direkt på det sätt som man skulle kunna mäta höjd eller vikt. Istället har forskarna en teori och konceptualisering av intelligens och designar sedan mätinstrument som ett frågeformulär eller test som ger dem flera indikatorer på intelligens. Dessa indikatorer kombineras sedan i en modell för att skapa ett rimligt sätt att mäta intelligens som en latent variabel (cirkeln för intelligens i figur 1) från indikatorerna (fyrkantiga rutor med skala 1–4 i figur 1). Figur 1 presenteras som en slutlig modell, efter att ha kört den och erhållit alla uppskattningar (siffrorna på pilarna). Det finns ingen konsensus om den bästa symboliska notationen för att representera SEM, till exempel representerar figur 2 en liknande modell som figur 1 utan lika många pilar och i ett format som kan förekomma innan modellen körs.

En stor fördel med SEM är att alla dessa mätningar och tester sker samtidigt i en statistisk uppskattningsprocedur, där felen genom hela modellen beräknas med hjälp av all information från modellen. Det betyder att felen är mer exakta än om en forskare skulle beräkna varje del av modellen separat.

Historia

Strukturell ekvationsmodellering (SEM) har sina rötter i Sewall Wrights arbete som tillämpade explicita kausala tolkningar på regressionsekvationer baserade på direkta och indirekta effekter av observerade variabler i populationsgenetik. Lee M. Wolfle sammanställde en kommenterad bibliografisk historia av Sewall Wrights vägkoefficientmetod som vi idag känner som vägmodellering . Wright lade till två viktiga element till standardpraxisen att använda regression för att förutsäga ett resultat. Dessa var (1) att kombinera information från mer än en regressionsekvation med hjälp av (2) ett kausalt tillvägagångssätt för regressionsmodellering snarare än enbart prediktivt. Sewall Wright konsoliderade sin metod för väganalys i sin artikel från 1934 "The Method of Path Coefficients".

Otis Dudley Duncan introducerade SEM till samhällsvetenskaperna 1975 och det blomstrade under hela 1970- och 80-talen. Olika men ändå matematiskt relaterade modelleringsmetoder utvecklade inom psykologi, sociologi och ekonomi. Konvergensen av två av dessa utvecklingsströmmar (faktoranalys från psykologi och väganalys från sociologi via Duncan) producerade den nuvarande kärnan av SEM även om det finns stor överlappning med ekonometriska metoder som använder samtidiga ekvationer och exogena (kausala variabler).

Ett av flera program Karl Gustav Jöreskog utvecklade i början av 1970-talet på Educational Testing Services ( LISREL ) innehöll latenta variabler (som psykologer kände till som de latenta faktorerna från faktoranalys) inom ekvationer i väganalysstil (som sociologer hade ärvt från Wright och Duncan ). Den faktorstrukturerade delen av modellen inkluderade mätfel och möjliggjorde därmed mätfelsjusterade uppskattningar av effekter som kopplar ihop latenta variabler.

Lös och förvirrande terminologi har använts för att dölja svagheter i metoderna. I synnerhet har PLS-PA (även känd som PLS-PM) sammanblandats med partiell minsta kvadraters regression PLSR, som är ett substitut för vanlig minsta kvadratregression och inte har något att göra med väganalys. PLS-PA har felaktigt marknadsförts som en metod som fungerar med små datamängder när andra uppskattningsmetoder misslyckas; i själva verket har det visat sig att minsta nödvändiga urvalsstorlekar för denna metod överensstämmer med de som krävs vid multipel regression.

Både LISREL och PLS-PA var tänkta som iterativa datoralgoritmer, med tonvikt från början på att skapa ett tillgängligt grafiskt och datainmatningsgränssnitt och förlängning av Wrights (1921) väganalys. Tidiga Cowles-kommissionens arbete med simultanekvationsuppskattning centrerade på Koopman och Hoods (1953) algoritmer från transportekonomi och optimal routing, med maximal sannolikhetsuppskattning och slutna algebraiska beräkningar, eftersom iterativa lösningssökningstekniker var begränsade under dagarna före datorer.

Anderson och Rubin (1949, 1950) utvecklade den begränsade informationens maximala sannolikhets-estimator för parametrarna för en enskild strukturell ekvation, som indirekt inkluderade tvåstegs minsta kvadrat- estimatorn och dess asymptotiska fördelning (Anderson, 2005) (Farebrother, 1999). Tvåstegs minsta kvadrater föreslogs ursprungligen som en metod för att uppskatta parametrarna för en enskild strukturell ekvation i ett system av linjära samtidiga ekvationer, som introducerades av Theil (1953a, 1953b, 1961) och mer eller mindre oberoende av Basmann (1957) och Sargan (1958). Andersons maximala sannolikhetsuppskattning av begränsad information implementerades så småningom i en datorsökningsalgoritm , där den konkurrerade med andra iterativa SEM-algoritmer. Av dessa var tvåstegs minsta kvadrater den överlägset mest använda metoden under 1960-talet och början av 1970-talet.

System av regressionsekvationer utvecklades vid Cowles-kommissionen från 1950-talet och framåt, vilket utökade transportmodelleringen av Tjalling Koopmans . Sewall Wright och andra statistiker försökte främja väganalysmetoder vid Cowles (då vid University of Chicago ). University of Chicago statistiker identifierade många fel med sökvägsanalysapplikationer inom samhällsvetenskaperna; fel som inte innebar betydande problem för att identifiera genöverföring i Wrights sammanhang, men som gjorde vägmetoder som PLS-PA och LISREL problematiska inom samhällsvetenskapen. Freedman (1987) sammanfattade dessa invändningar i väganalyser: "underlåtenhet att skilja mellan orsaksantaganden, statistiska implikationer och policypåståenden har varit en av huvudorsakerna till misstankarna och förvirringen kring kvantitativa metoder inom samhällsvetenskapen" (se även Wolds (1987). 1987) svar). Wrights väganalys fick aldrig någon större anslutning bland amerikanska ekonometriker, men lyckades påverka Hermann Wold och hans elev Karl Jöreskog . Jöreskogs elev Claes Fornell främjade LISREL i USA.

Framsteg inom datorer gjorde det enkelt för nybörjare att tillämpa strukturella ekvationsmetoder i den datorintensiva analysen av stora datamängder i komplexa, ostrukturerade problem. De mest populära lösningsteknikerna delas in i tre klasser av algoritmer: (1) vanliga minsta kvadratalgoritmer som appliceras oberoende av varje väg, såsom de tillämpas i de så kallade PLS-väganalyspaketen som uppskattar med OLS; (2) algoritmer för kovariansanalys som utvecklats från verk av Wold och hans elev Karl Jöreskog implementerade i LISREL, AMOS och EQS; och (3) regressionsalgoritmer för simultanekvationer utvecklade vid Cowles Commission av Tjalling Koopmans.

Pearl har utökat SEM från linjära till icke-parametriska modeller och föreslagit kausala och kontrafaktiska tolkningar av ekvationerna. Om man till exempel utesluter en variabel Z från argumenten i en ekvation hävdar att den beroende variabeln är oberoende av ingrepp på den exkluderade variabeln, när vi väl håller de återstående argumenten konstant. Icke-parametriska SEM:er tillåter uppskattning av totala, direkta och indirekta effekter utan att göra någon förpliktelse till formen av ekvationerna eller fördelningarna av feltermerna. Detta utökar medlingsanalys till system som involverar kategoriska variabler i närvaro av icke-linjära interaktioner. Bollen och Pearl undersöker historien om den kausala tolkningen av SEM och varför det har blivit en källa till förvirring och kontroverser.

SEM-väganalysmetoder är populära inom samhällsvetenskapen på grund av deras tillgänglighet; paketerade datorprogram gör det möjligt för forskare att få resultat utan besväret med att förstå experimentell design och kontroll, effekt och urvalsstorlekar och många andra faktorer som är en del av god forskningsdesign. Anhängare säger att detta återspeglar en holistisk och mindre flagrant kausal tolkning av många verkliga fenomen – särskilt inom psykologi och social interaktion – än vad som kan antas inom naturvetenskapen; belackare tyder på att många felaktiga slutsatser har dragits på grund av denna brist på experimentell kontroll. [ citat behövs ]

Riktning i de riktade nätverksmodellerna av SEM uppstår från förmodade orsak-verkan-antaganden om verkligheten. Sociala interaktioner och artefakter är ofta epifenomen – sekundära fenomen som är svåra att direkt koppla till kausala faktorer. Ett exempel på ett fysiologiskt epifenomen är till exempel tid att genomföra en 100-meterssprint. En person kanske kan förbättra sin sprinthastighet från 12 sekunder till 11 sekunder, men det kommer att vara svårt att tillskriva den förbättringen till några direkta orsaksfaktorer, som kost, attityd, väder, etc. 1 sekunds förbättringen i sprinttid är en epifenomen – den holistiska produkten av interaktion mellan många individuella faktorer.

Allmän syn på SEM

Även om varje teknik i SEM-familjen är olika, är följande aspekter gemensamma för många SEM-metoder, eftersom det kan sammanfattas som ett 4E-ramverk av många SEM-forskare som Alex Liu, det vill säga 1) Ekvation (modell- eller ekvationsspecifikation), 2 ) Uppskattning av fria parametrar, 3) Utvärdering av modeller och modellanpassning, 4) Förklaring och kommunikation, samt utförande av resultat.

Modellspecifikation

Två huvudkomponenter av modeller urskiljs i SEM: den strukturella modellen som visar potentiella orsakssamband mellan endogena och exogena variabler, och mätmodellen som visar sambanden mellan latenta variabler och deras indikatorer. Undersökande och bekräftande faktoranalysmodeller innehåller till exempel endast mätdelen, medan vägdiagram kan ses som SEM som endast innehåller den strukturella delen.

När modelleraren specificerar vägar i en modell kan modelleraren ange två typer av samband: (1) fria vägar, där hypotetiska kausala (i själva verket kontrafaktiska) samband mellan variabler testas, och därför lämnas "fria" att variera, och (2 ) samband mellan variabler som redan har ett uppskattat samband, vanligtvis baserat på tidigare studier, som är "fasta" i modellen.

En modellerare kommer ofta att specificera en uppsättning teoretiskt rimliga modeller för att bedöma om den föreslagna modellen är den bästa av uppsättningen av möjliga modeller. Inte bara måste modelleraren redogöra för de teoretiska skälen för att bygga modellen som den är, utan modelleraren måste också ta hänsyn till antalet datapunkter och antalet parametrar som modellen måste uppskatta för att identifiera modellen.

En identifierad modell är en modell där ett specifikt parametervärde unikt identifierar modellen ( rekursiv definition ), och ingen annan likvärdig formulering kan ges av ett annat parametervärde. En datapunkt är en variabel med observerade poäng, som en variabel som innehåller poängen på en fråga eller antalet gånger respondenterna köper en bil. Parametern är värdet av intresse, vilket kan vara en regressionskoefficient mellan den exogena och den endogena variabeln eller faktorbelastningen (regressionskoefficient mellan en indikator och dess faktor). Om det finns färre datapunkter än antalet uppskattade parametrar är den resulterande modellen "oidentifierad", eftersom det finns för få referenspunkter för att ta hänsyn till all varians i modellen. Lösningen är att begränsa en av vägarna till noll, vilket innebär att den inte längre ingår i modellen.

Uppskattning av fria parametrar

Parameteruppskattning görs genom att jämföra de faktiska kovariansmatriserna som representerar sambanden mellan variabler och de uppskattade kovariansmatriserna för den bäst passande modellen. Detta erhålls genom numerisk maximering via förväntan–maximering av ett passningskriterium som tillhandahålls av maximal sannolikhetsuppskattning , kvasi-maximal sannolikhetsuppskattning , viktade minsta kvadrater eller asymptotiskt distributionsfria metoder. Detta görs ofta genom att använda ett specialiserat SEM-analysprogram, av vilket flera finns.

Utvärdering av modeller och modellpassning

Efter att ha uppskattat en modell kommer analytiker att vilja tolka modellen. Uppskattade vägar kan tabelleras och/eller presenteras grafiskt som en vägmodell. Variablernas inverkan bedöms med hjälp av banspårningsregler (se sökvägsanalys ) .

Det är viktigt att undersöka "passningen" av en uppskattad modell för att avgöra hur väl den modellerar data. Detta är en grundläggande uppgift i SEM-modellering, som utgör grunden för att acceptera eller förkasta modeller och, mer vanligtvis, acceptera en konkurrerande modell framför en annan. Resultatet av SEM-program inkluderar matriser för de uppskattade sambanden mellan variabler i modellen. Bedömning av passform beräknar i huvudsak hur lika de förutsagda data är matriser som innehåller sambanden i den faktiska datan.

Formella statistiska tester och passningsindex har utvecklats för dessa ändamål. Individuella parametrar för modellen kan också undersökas inom den skattade modellen för att se hur väl den föreslagna modellen passar körteorin. De flesta, men inte alla, uppskattningsmetoder gör sådana tester av modellen möjliga.

Naturligtvis, som i alla statistiska hypotestester , är SEM-modelltester baserade på antagandet att korrekt och fullständig relevant data har modellerats. I SEM-litteraturen har diskussion om passform lett till en mängd olika rekommendationer om den exakta tillämpningen av de olika passformsindexen och hypotestesterna.

Det finns olika sätt att bedöma passform. Traditionella metoder för modellering utgår från en nollhypotes , som belönar mer sparsamma modeller (dvs. de med färre fria parametrar), till andra som AIC som fokuserar på hur lite de anpassade värdena avviker från en mättad modell [ citat behövs ] (dvs. hur väl de reproducera de uppmätta värdena), med hänsyn till antalet fria parametrar som används. Eftersom olika passformsmått fångar olika delar av modellens passform är det lämpligt att rapportera ett urval av olika passformsmått. Riktlinjer (dvs. "cutoff-poäng") för att tolka passformsmått, inklusive de som listas nedan, är föremål för mycket debatt bland SEM-forskare.

Några av de mer vanliga måtten för passform inkluderar

  • Chi-kvadrat
    • Ett grundläggande mått på passform som används i beräkningen av många andra passformsmått. Det är en funktion av urvalsstorleken och diskrepansen mellan den observerade kovariansmatrisen och modellkovariansmatrisen.
  • Akaike informationskriterium (AIC)
    • Ett test av relativ modellpassning: Den föredragna modellen är den med det lägsta AIC-värdet.
    • där k är antalet parametrar i den statistiska modellen , och L är det maximerade värdet av sannolikheten för modellen.
  • Root Mean Square Error of Approximation (RMSEA)
    • Fit index där ett värde på noll indikerar bästa passform. Även om riktlinjen för att bestämma en "nära passform" med RMSEA är mycket omtvistad, är de flesta forskare överens om att en RMSEA på 0,1 eller mer indikerar dålig passform.
  • Standardiserad Root Mean Squared Residual (SRMR)
    • SRMR är en populär indikator för absolut passform. Hu och Bentler (1999) föreslog .08 eller mindre som en riktlinje för god passform. Kline (2011) föreslog .1 eller mindre som en riktlinje för bra passform.
  • Comparative Fit Index (CFI)
    • Vid undersökning av baslinjejämförelser beror CFI till stor del på den genomsnittliga storleken på korrelationerna i data. Om den genomsnittliga korrelationen mellan variabler inte är hög, kommer CFI inte att vara särskilt hög. Ett CFI-värde på .95 eller högre är önskvärt.

För varje mått på passform måste ett beslut om vad som representerar en tillräckligt bra passform mellan modellen och data spegla andra kontextuella faktorer som urvalsstorlek , förhållandet mellan indikatorer och faktorer och modellens övergripande komplexitet. Till exempel, mycket stora urval gör Chi-kvadrattestet alltför känsligt och mer sannolikt att indikera bristande modell-datapassning.

Modell modifiering

Modellen kan behöva modifieras för att förbättra passformen och därigenom uppskatta de mest sannolika sambanden mellan variabler. Många program tillhandahåller modifikationsindex som kan vägleda mindre ändringar. Modifieringsindex rapporterar förändringen i χ² som är ett resultat av att frigöra fasta parametrar: vanligtvis lägger man därför till en sökväg till en modell som för närvarande är nollställd. Ändringar som förbättrar modellanpassningen kan flaggas som potentiella ändringar som kan göras i modellen. Modifieringar av en modell, särskilt den strukturella modellen, är förändringar av den teori som påstås vara sann. Modifieringar måste därför vara vettiga i termer av teorin som testas, eller erkännas som begränsningar för den teorin. Ändringar i mätmodellen är i själva verket påståenden om att objekten/data är orena indikatorer på de latenta variabler som specificeras av teorin.

Modeller bör inte ledas av modifieringsindex, som Maccallum (1986) visade: "även under gynnsamma förhållanden måste modeller som härrör från specifikationssökningar betraktas med försiktighet."

Provstorlek och kraft

Medan forskare är överens om att stora urvalsstorlekar krävs för att ge tillräcklig statistisk kraft och exakta uppskattningar med hjälp av SEM, finns det ingen allmän konsensus om den lämpliga metoden för att bestämma adekvat urvalsstorlek. Generellt sett inkluderar övervägandena för att bestämma urvalsstorleken antalet observationer per parameter, antalet observationer som krävs för att passningsindex ska fungera adekvat och antalet observationer per frihetsgrad. Forskare har föreslagit riktlinjer baserade på simuleringsstudier, yrkeserfarenhet och matematiska formler.

Kraven på provstorlekar för att uppnå en viss signifikans och kraft i SEM-hypotestestning är liknande för samma modell när någon av de tre algoritmerna (PLS-PA, LISREL eller system av regressionsekvationer) används för testning. [ citat behövs ]

Förklaring och kommunikation

Uppsättningen av modeller tolkas sedan så att påståenden om konstruktionerna kan göras, baserat på den bäst passande modellen.

Försiktighet bör alltid iakttas när man gör påståenden om kausalitet även när experiment eller tidsbestämda studier har gjorts. Begreppet kausal modell måste förstås som "en modell som förmedlar kausala antaganden", inte nödvändigtvis en modell som producerar validerade kausala slutsatser. Att samla in data vid flera tidpunkter och använda en experimentell eller kvasi-experimentell design kan hjälpa till att utesluta vissa rivaliserande hypoteser, men även ett randomiserat experiment kan inte utesluta alla sådana hot mot kausala slutsatser. God anpassning av en modell som överensstämmer med en kausalhypotes innebär undantagslöst lika god anpassning av en annan modell som överensstämmer med en motsatt orsakshypotes. Ingen forskningsdesign, hur smart den än är, kan hjälpa till att särskilja sådana rivaliserande hypoteser, förutom interventionella experiment.

Som i vilken vetenskap som helst, kommer efterföljande replikering och kanske modifiering att utgå från det första fyndet.

Avancerade användningsområden

SEM-specifik programvara

Det finns många mjukvarupaket för att passa strukturella ekvationsmodeller. LISREL var den första sådan mjukvaran, som ursprungligen släpptes på 1970-talet. Ofta använda mjukvaruimplementationer bland forskare inkluderar Mplus, R -paket lavaan och sem, LISREL , OpenMx , SPSS AMOS och Stata . Barbara M. Byrne publicerade flera instruktionsböcker för att använda en mängd av dessa mjukvaror som en del av Society of Multivariate Experimental Psychologys bokserie Multivariate Applications.

Forskare anser att det är god praxis att rapportera vilket programvarupaket och vilken version som användes för SEM-analys eftersom de har olika möjligheter och kan använda lite olika metoder för att utföra liknande tekniker.

Se även

Bibliografi

Vidare läsning

externa länkar

Hämtad från " https://en.wikipedia.org/w/index.php?title=Structural_equation_modeling&oldid=1143769743 "