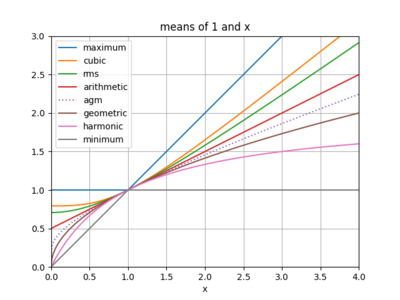
Aritmetiskt–geometriskt medelvärde

Rita av det aritmetiskt-geometriska medelvärdet

\operatorname {agm} (1,x)

längs flera generaliserade medel .

I matematik är det aritmetiskt-geometriska medelvärdet av två positiva reella tal $x$ och $y$ den ömsesidiga gränsen för en sekvens av aritmetiska medelvärden och en sekvens av geometriska medelvärden :

Börja sekvenserna med x och y :

{\begin{aligned}a_{0}&=x,\\g_{0}&=y.\end{aligned}}

Definiera sedan de två beroende sekvenserna $(a n)$ och $(g n)$ som

{\begin{aligned}a_{n+1}&={\tfrac {1}{2}}(a_{n}+g_{n}),\\g_{n+1}&={ \sqrt {a_{n}g_{n}}}\,.\end{aligned}}

Dessa två sekvenser konvergerar till samma tal, det aritmetiskt-geometriska medelvärdet av $x$ och $y$ ; det betecknas med $M (x, y)$ , eller ibland med $agm(x, y)$ eller $AGM(x, y)$ .

Det aritmetiska-geometriska medelvärdet används i snabba algoritmer för exponentiella och trigonometriska funktioner , såväl som vissa matematiska konstanter , i synnerhet vid beräkning av $π$ .

Det aritmetiskt-geometriska medelvärdet kan utökas till komplexa tal och när grenarna av kvadratroten tillåts tas inkonsekvent är det i allmänhet en flervärdig funktion .

Exempel

För att hitta det aritmetiskt-geometriska medelvärdet av $0 a = 24$ och $0 g = 6$ , iterera enligt följande:

stil {array}{rcccl}a_{1}&=&{\tfrac {1}{2}}(24+6)&=&15\\g_{1}&=&{\sqrt {24\cdot 6}} &=&12\\a_{2}&=&{\tfrac {1}{2}}(15+12)&=&13.5\\g_{2}&=&{\sqrt {15\cdot 12} }&=&13.416\ 407\ 8649\dots \\&&\vdots &&\end{array}}}

De första fem iterationerna ger följande värden:

$n$	$ett n$	$g n$
0	24	6
1	1 5	1 2
2	13 .5	13 .416 407 864 998 738 178 455 042...
3	13.458 203 932 499 369 089 227 521...	13,458 139 030 990 984 877 207 090...
4	13,458 171 481 7 45 176 983 217 305...	13.458 171 481 7 06 053 858 316 334...
5	13,458 171 481 725 615 420 766 8 20...	13.458 171 481 725 615 420 766 8 06...

Antalet siffror där $a n$ och $g n$ överensstämmer (understrukna) fördubblas ungefär med varje iteration. Det aritmetiskt-geometriska medelvärdet av 24 och 6 är den gemensamma gränsen för dessa två sekvenser, som är ungefär 13.458 171 481 725 615 420 766 813 156 974 399 243 053 838 8544 .

Historia

Lagranges verk . Dess egenskaper analyserades ytterligare av Gauss .

Egenskaper

Det geometriska medelvärdet av två positiva tal är aldrig större än det aritmetiska medelvärdet (se olikhet mellan aritmetiska och geometriska medelvärden ) . Som en konsekvens, för $(a n)$ $> > 0$ , $(g n)$ is an increasing sequence, is a decreasing sequence, and $g n \leq M (x, y) \leq a n$ . These are strict inequalities if $x \neq y$ .

$M (x, y)$ är alltså ett tal mellan det geometriska och aritmetiska medelvärdet av $x$ och $y$ ; det är också mellan $x$ och $y$ .

Om $r \geq 0$ så är $M (rx, ry) = r M (x, y)$ .

Det finns ett uttryck i integralform för $M (x y) :$ ,

{\begin{aligned}M(x,y)&={\frac {\pi }{2}}\left (\int _{0}^{\frac {\pi }{2}}{\frac {d\theta }{\sqrt {x^{2}\cos ^{2}\theta +y^{2} \sin ^{2}\theta }}}\right)^{-1}\\&=\pi \left(\int _{0}^{\infty }{\frac {dt}{\sqrt {t (t+x^{2})(t+y^{2})}}}\höger)^{-1}\\&={\frac {\pi}{4}}\cdot {\frac { x+y}{K\left({\frac {xy}{x+y}}\right)}}\end{aligned}}

där $K (k)$ är den fullständiga elliptiska integralen av det första slaget :

K(k)=\int _{0}^{\frac {\pi }{2}}{\frac { d\theta }{\sqrt {1-k^{2}\sin ^{2}(\theta )}}}

Faktum är att eftersom den aritmetisk-geometriska processen konvergerar så snabbt, ger den ett effektivt sätt att beräkna elliptiska integraler via denna formel. Inom tekniken används det till exempel i elliptisk filterdesign .

Det aritmetiska–geometriska medelvärdet är kopplat till Jacobi theta-funktionen $\theta _{3}$ med

M(1,x)=\theta _{3}^{-2}\left(\exp \left(-\pi { \frac {M(1,x)}{M\left(1,{\sqrt {1-x^{2}}}\right)}}\right)\right)=\left(\summa _{n \in \mathbb {Z} }\exp \left(-n^{2}\pi {\frac {M(1,x)}{M\left(1,{\sqrt {1-x^{2} }}\right)}}\right)\right)^{-2},

som vid inställning av $x=1/{\sqrt {2}}$ ger

M(1,1/{\sqrt {2}})=\left(\sum _{n\in \mathbb {Z}}e^{-n^{2}\pi}\right)^ {-2}.

Relaterade begrepp

Den reciproka av det aritmetiskt-geometriska medelvärdet av 1 och kvadratroten av 2 kallas Gauss konstant , efter Carl Friedrich Gauss .

{\frac {1}{M(1,{\sqrt {2}})}}=G=0,8346268\dots

1799 bevisade Gauss det

M(1,{\sqrt {2}})={\frac {\pi }{\varpi }}

där $\varpi$ är lemniscatkonstanten .

År 1941 bevisades $M(1,{\sqrt {2}})$ (och därmed ${\displaystyle G} )$ transcendental av Theodor Schneider . Mängden $\{\pi ,M(1,1/{\sqrt {2}})\}$ är algebraiskt oberoende över $\mathbb { Q}$ , men mängden $\{\pi ,M(1,1/{\sqrt {2}} ),M'(1,1/{\sqrt {2}})\}$ (där primtal anger derivatan med avseende på den andra variabeln) är inte algebraiskt oberoende av $\mathbb {Q}$ . Faktiskt,

\pi =2{\sqrt {2}}{\frac {M^{3}(1,1/{\sqrt {2}})}{M'(1,1/{\sqrt {2 }})}}.

Det geometriska–harmoniska medelvärdet kan beräknas med en analog metod, med hjälp av sekvenser av geometriska och övertonska medel. Man finner att $GH(x,y) = 1/M(1/ x, 1/ y) = xy /M(x,y)$ . Det aritmetiska–harmoniska medelvärdet kan definieras på liknande sätt, men har samma värde som det geometriska medelvärdet (se avsnittet "Beräkning" där ) .

Det aritmetiska–geometriska medelvärdet kan användas för att beräkna – bland annat – logaritmer , kompletta och ofullständiga elliptiska integraler av första och andra slaget, och Jacobi elliptiska funktioner .

Bevis på existens

Från olikheten mellan aritmetiska och geometriska medel kan vi dra slutsatsen att:

g_{n}\leq a_{n}

och sålunda

g_{n+1}={\sqrt {g_{n}\cdot a_{n}}}\geq {\sqrt {g_{n}\cdot g_{n}}}=g_{n}

det vill säga sekvensen $g n$ är icke-minskande.

Vidare är det lätt att se att det också ovanför avgränsas av det större av $x$ och $y$ (vilket följer av att både det aritmetiska och geometriska medelvärdet för två tal ligger mellan dem). Således, genom den monotona konvergenssatsen , är sekvensen konvergent, så det finns ett $g$ så att:

\lim _{n\to \infty }g_{n}=g

Men vi kan också se att:

a_{n}={\frac {g_{n+1}^{2}}{g_{n}}}

och så:

\lim _{n\to \infty }a_{n}=\lim _{n\to \ infty }{\frac {g_{n+1}^{2}}{g_{n}}}={\frac {g^{2}}{g}}=g

QED

Bevis på uttrycket integralform

Detta bevis ges av Gauss. Låta

I(x,y)=\int _{0}^{\pi /2} {\frac {d\theta }{\sqrt {x^{2}\cos ^{2}\theta +y^{2}\sin ^{2}\theta }}},

Ändra integrationsvariabeln till $\theta '$ , där

\sin \theta ={\frac {2x\sin \theta '}{(x+ y)+(xy)\sin ^{2}\theta '}},

ger

{\begin{aligned}I(x,y)&=\int _{0}^{\pi /2}{\frac {d\theta '}{\sqrt {{\bigl (}{\ frac {1}{2}}(x+y){\bigr )}^{2}\cos ^{2}\theta '+{\bigl (}{\sqrt {xy}}{\bigr )}^ {2}\sin ^{2}\theta '}}}\\&=I{\bigl (}{\tfrac {1}{2}}(x+y),{\sqrt {xy}}{\ bigr )}.\end{aligned}}

Det har vi alltså

{\begin{aligned}I(x,y)&=I(a_{1},g_{1})=I(a_{2},g_{2})=\cdots \\&=I {\bigl (}M(x,y),M(x,y){\bigr )}=\pi /{\bigr (}2M(x,y){\bigl )}.\end{aligned}}

Den sista likheten kommer från att observera att

I(z,z)=\pi /(2z)

.

Slutligen får vi det önskade resultatet

M(x,y)=\pi /{\bigl (}2I(x,y){\bigr )}.

Ansökningar

Siffran π

Till exempel, enligt Gauss-Legendre-algoritmen :

\pi ={\frac {4\,M(1,1/{\sqrt { 2}})^{2}}{1-\displaystyle \sum _{j=1}^{\infty }2^{j+1}c_{j}^{2}}},

var

c_{j}={\frac {1}{2}}\left(a_{j-1}-g_{j-1 }\höger),

med $a_{0}=1$ och ${\displaystyle g_{0}=1/{\sqrt {2}}} ,$ som kan beräknas utan förlust av

c_{j}={\frac {c_{j-1}^{2}}{4a_{j}}}.

Komplett elliptisk integral K (sin α )

Att ta $a_{0}=1$ och $g_{0}=\cos \alpha$ ger årsstämman

M(1,\cos \alpha )={\frac {\pi }{2K(\sin \alpha )}},

där $K (k)$ är en komplett elliptisk integral av det första slaget :

K(k)=\int _{0}^{\pi /2}(1-k^{2}\sin ^{2}\theta )^{-1/2}\,d\theta .

Det vill säga att denna kvartalsperiod kan beräknas effektivt genom årsstämman,

K(k)={\frac {\pi }{2M(1,{\sqrt {1-k^{2}}})}}.

Andra applikationer

Genom att använda denna egenskap hos AGM tillsammans med de stigande transformationerna av John Landen, föreslog Richard P. Brent de första AGM-algoritmerna för snabb utvärdering av elementära transcendentala funktioner ( $e x$ , $cos x$ , $sin x )$ . Därefter fortsatte många författare med att studera användningen av AGM-algoritmerna.

Se även

Anteckningar

Citat

Källor

Daróczy, Zoltán; Páles, Zsolt (2002). "Gauss-komposition av medel och lösningen av Matkowski-Suto-problemet". Publicationes Mathematicae Debrecen . 61 (1–2): 157–218.
"Arithmetic–geometric mean process" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
Weisstein, Eric W. "Aritmetiskt–geometriskt medelvärde" . MathWorld .