Dihedral symmetri i tre dimensioner

Valda punktgrupper i tre dimensioner
Polyedrisk grupp , [n,3], (*n32)
Involutionssymmetri C _s , (*) [ ] =	Cyklisk symmetri C _nv , (*nn) [n] =	Dihedral symmetri D _nh , (*n22) [n,2] =
Tetraedrisk symmetri Td _, (*332) [3,3] =	Oktaedrisk symmetri O _h , (*432) [4,3] =	Ikosaedrisk symmetri I _h , (*532) [5,3] =

Inom geometri är dihedrisk symmetri i tre dimensioner en av tre oändliga sekvenser av punktgrupper i tre dimensioner som har en symmetrigrupp som som abstrakt grupp är en dihedrisk grupp Dih _n (för n ≥ 2).

Typer

Det finns 3 typer av dihedral symmetri i tre dimensioner, var och en visas nedan i 3 notationer: Schönflies notation , Coxeter notation och orbifold notation .

Chiral

D _n , [ n ,2] ⁺ , (22 n ) av ordningen 2 n – dihedrisk symmetri eller para-n-gonal grupp (abstrakt grupp: Dih _n ).

Achiral

D _nh , [ n ,2], (*22 n ) av ordningen 4 n – prismatisk symmetri eller full orto-n-gonal grupp (abstrakt grupp: Dih _n × Z ₂ ).
D _nd (eller D _nv ), [2 n ,2 ⁺ ], (2* n ) av ordningen 4 n – antiprismatisk symmetri eller full gyro-n-gonal grupp (abstrakt grupp: Dih _{2 n} ).

För ett givet n har alla tre n -faldig rotationssymmetri kring en axel ( rotation med en vinkel på 360°/ n ändrar inte objektet), och 2-faldig rotationssymmetri kring en vinkelrät axel, därav ungefär n av dessa. För n = ∞ motsvarar de tre frisgrupper . Schönflies notation används, med Coxeter notation inom parentes och orbifold notation inom parentes. Termen horisontell (h) används med avseende på en vertikal rotationsaxel.

I 2D inkluderar symmetrigruppen Dn _. reflektioner i linjer När 2D-planet är inbäddat horisontellt i ett 3D-utrymme kan en sådan reflektion antingen ses som begränsningen till det planet av en reflektion genom ett vertikalplan, eller som begränsningen till planet för en rotation kring reflektionslinjen, med 180 °. I 3D särskiljs de två operationerna: gruppen Dn innehåller endast rotationer _, inte reflektioner. Den andra gruppen är pyramidal symmetri C _nv av samma ordning, 2 n .

Med reflektionssymmetri i ett plan vinkelrätt mot den n -faldiga rotationsaxeln har vi D _nh , [n], (*22 n ).

D _nd (eller D _nv ), [2 n ,2 ⁺ ], (2* n ) har vertikala spegelplan mellan de horisontella rotationsaxlarna, inte genom dem. Som ett resultat är den vertikala axeln en 2n - faldig rotorreflektionsaxel .

D _nh är symmetrigruppen för ett regelbundet n -sidigt prisma och även för en vanlig n-sidig bipyramid . D _nd är symmetrigruppen för en regelbunden n -sidig antiprisma , och även för en regelbunden n-sidig trapetsoeder . D _n är symmetrigruppen för ett delvis roterat prisma.

n = 1 ingår inte eftersom de tre symmetrierna är lika med andra:

D1 och C2 : grupp av ordning 2 med en enda 180° _rotation_.
D _{1 h} och C _{2 v} : grupp av ordning 4 med en reflektion i ett plan och en 180° rotation kring en linje i det planet.
D _{1 d} och C _{2 h} : grupp av ordning 4 med en reflektion i ett plan och en 180° rotation kring en linje vinkelrät mot det planet.

För n = 2 finns det inte en huvudaxel och två ytterligare axlar, utan det finns tre ekvivalenta.

D ₂ , [2,2] ⁺ , (222) av ordning 4 är en av de tre symmetrigrupptyperna med Klein-fyragruppen som abstrakt grupp. Den har tre vinkelräta 2-faldiga rotationsaxlar. Det är symmetrigruppen av en kuboid med ett S skrivet på två motsatta ytor, i samma orientering.
D _{2 h} , [2,2], (*222) av ordning 8 är symmetrigruppen för en kuboid.
D _{2 d} , [4,2 ⁺ ], (2*2) av ordning 8 är symmetrigruppen av t.ex.
- En kvadratisk kuboid med en diagonal ritad på en kvadratisk yta och en vinkelrät diagonal på den andra.
- En vanlig tetraeder skalad i riktning mot en linje som förbinder mittpunkterna på två motsatta kanter ( D _{2 d} är en undergrupp av T _d ; genom skalning minskar vi symmetrin).

Undergrupper

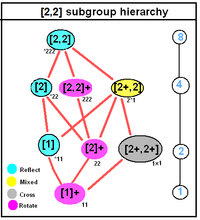D _2h , [2,2], (*222)	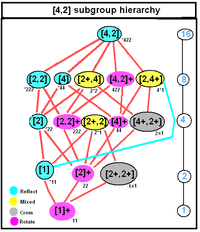D _4h , [4,2], (*224)

För D _nh , [n,2], (*22n), ordning 4n

C _nh , [n ⁺ ,2], (n*), ordning 2n
C _nv , [n,1], (*nn), ordning 2n
D _n , [n,2] ⁺ , (22n), ordning 2n

För D _nd , [2n,2 ⁺ ], (2*n), ordning 4n

S _{2 n} , [2n ⁺ ,2 ⁺ ], (n×), ordning 2n
C _nv , [n ⁺ ,2], (n*), ordning 2n
D _n , [n,2] ⁺ , (22n), ordning 2n

D _nd är också en undergrupp av D _{2 nh} .

Exempel

D _2h , [2,2], (*222) Order 8	D _2d , [4,2 ⁺ ], (2*2) Ordning 8	D _3h , [3,2], (*223) Order 12
basket sömbanor	baseballsömbanor (ignorerar sömmens riktning )	Badboll (ignorerar färger)

D _nh , [ n ], (*22 n ):

prismor

D _{5 h} , [5], (*225):

Pentagrammisk prisma	Pentagrammisk antiprism

D _{4 d} , [8,2 ⁺ ], (2*4):

Snub fyrkantig antiprisma

D _{5 d} , [10,2 ⁺ ], (2*5):

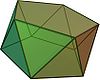Pentagonal antiprisma	Pentagrammisk korsad antiprism	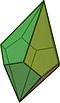femkantig trapetsoeder

D _{17 d} , [34,2 ⁺ ], (2*17):

Heptadekagonal antiprisma

Se även

Coxeter , HSM och Moser, WOJ (1980). Generatorer och relationer för diskreta grupper . New York: Springer-Verlag. ISBN 0-387-09212-9 . {{ citera bok }} : CS1 underhåll: flera namn: lista över författare ( länk )
NW Johnson : Geometries and Transformations , (2018) ISBN 978-1-107-10340-5 Kapitel 11: Finita symmetrigrupper , 11.5 sfäriska Coxeter-grupper
Conway, John Horton ; Huson, Daniel H. (2002), "The Orbifold Notation for Two-Dimensional Groups", Structural Chemistry , Springer Netherlands, 13 (3): 247–257, doi : 10.1023/A:1015851621002

externa länkar

Grafisk översikt av de 32 kristallografiska punktgrupperna – bildar de första delarna (förutom att hoppa över n =5) av de 7 oändliga serierna och 5 av de 7 separata 3D-punktgrupperna