Rose (matematik)

För topologisk användning, se Rose (topologi) .

Rosor specificerade av sinusformen $r=\cos(k\theta )$ för olika rationellt numrerade värden för vinkelfrekvensen k = n / d . Rosor specificerade av $r=\sin(k\theta )$ är rotationer av dessa rosor med en fjärdedels period av sinusformen i motsols riktning kring polen (ursprung). För korrekt matematisk analys måste ${\displaystyle k} uttryckas i irreducerbar form.$

I matematik är en ros- eller rhodoneakurva en sinusform som specificeras av antingen cosinus- eller sinusfunktionerna utan fasvinkel som plottas i polära koordinater . Rosekurvor eller "rhodonea" namngavs av den italienske matematikern som studerade dem, Guido Grandi , mellan åren 1723 och 1728.

Generell översikt

Specifikation

En ros är uppsättningen av punkter i polära koordinater som anges av den polära ekvationen

$r=a\cos(k\theta )$

eller i kartesiska koordinater med hjälp av de parametriska ekvationerna

$x=r\cos(\theta )=a\cos(k\theta )\cos(\theta )$

$y=r\sin(\theta )=a\cos(k\theta )\sin(\theta )$ .

Rosor kan också specificeras med sinusfunktionen. Eftersom

$\sin(k\theta )=\cos \left(k\theta -{ \frac {\pi }{2}}\right)=\cos \left(k\left(\theta -{\frac {\pi }{2k}}\right)\right)$ .

Således är rosen specificerad av $\,r=a\sin(k\theta )$ identisk med den som anges av $\ ,r=a\cos(k\theta )$ roterad moturs med $\pi /2k$ radianer, vilket är en fjärdedel av perioden för endera sinusformen.

Eftersom de specificeras med hjälp av cosinus- eller sinusfunktionen, uttrycks rosor vanligtvis som polära koordinat (snarare än kartesiska koordinater ) grafer av sinusoider som har vinkelfrekvensen k $\displaystyle k}$ och en amplitud av $a$ som bestämmer den radiella koordinaten $(r)$ givet den polära vinkeln $(\theta )$ (men när $k$ är ett rationellt tal kan en rosenkurva uttryckas i kartesiska koordinater eftersom de kan anges som algebraiska kurvor ).

Generella egenskaper

Rosor är direkt relaterade till egenskaperna hos sinusoiderna som anger dem.

Kronblad

• Grafer av rosor är sammansatta av kronblad . Ett kronblad är formen som bildas av grafen för en halvcykel av sinusformen som anger rosen. (En cykel är en del av en sinusform som är en period $T=2\pi /k$ lång och består av en positiv halvcykel, den kontinuerliga uppsättningen punkter där ${\ displaystyle r\geq 0}$ och är $T/2=\pi /k$ lång, och en negativ halvcykel är den andra halvan där $r\leq 0$ .)
  • Formen på varje kronblad är densamma eftersom graferna för halvcykler har samma form. Formen ges av den positiva halvcykeln med krön vid $(a,0)$ specificerad av $r=a\cos(k\theta )$ (som begränsas av vinkelintervallet ${\displaystyle -T/4\leq \theta \leq T/4} )$ . Kronbladet är symmetriskt kring polaxeln. Alla andra kronblad är rotationer av detta kronblad runt polen, inklusive de för rosor som anges av sinusfunktionen med samma värden för $a$ och $k$ .
  • I överensstämmelse med reglerna för att plotta punkter i polära koordinater kan en punkt i en negativ halvcykel inte plottas vid sin polära vinkel eftersom dess radiella koordinat r {\ $r}$ är negativ. Punkten plottas genom att addera $\pi$ radianer till den polära vinkeln med en radiell koordinat $|r|$ . Således kan positiva och negativa halvcykler vara sammanfallande i grafen för en ros. Dessutom är rosor inskrivna i cirkeln $r=a$ .
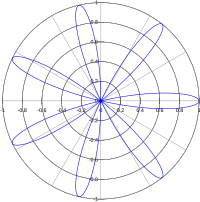
  • När perioden $T$ för sinusformen är mindre än eller lika med ${\displaystyle 4\pi } ,$ är kronbladets form en enda sluten slinga. En enda slinga bildas eftersom vinkelintervallet för en polär plot är $2\pi$ och vinkelbredden för halvcykeln är mindre än eller lika med $2\pi$ . När $T>4\pi$ (eller $|k|<1/2$ ) kan plottet av en halvcykel ses som en spiral ut från pol i mer än en krets runt polen tills plottning når den inskrivna cirkeln där den spiralerar tillbaka till polen, skär sig själv och bildar en eller flera slingor längs vägen. Följaktligen bildar varje kronblad 2 slingor när $4\pi <T\leq 8\pi$$\leq |k|<1/2}$ | ), 3 slingor när $\displaystyle 8\pi <T\leq 12\pi }$$displaystyle 1/6\leq |k|<1/4}$ ≤ ), etc. Rosor med endast ett kronblad med flera slingor observeras för $k=1/3,k=1/5,k=1/7,etc.$ (Se bilden i introduktionsavsnittet.)
  • En ros kronblad kommer inte att skära varandra när vinkelfrekvensen $k$ är ett heltal som inte är noll; annars skär kronbladen varandra.

Symmetri

Alla rosor visar en eller flera former av symmetri på grund av de underliggande symmetriska och periodiska egenskaperna hos sinusoider.

• En ros specificerad som $r=a\cos(k\theta )$ är symmetrisk kring polaxeln (linjen ${\displaystyle \theta =0} )$ på grund av identitet $a\cos(k\theta )=a\cos(-k\theta )$ som gör att rosorna som specificeras av de två polära ekvationerna sammanfaller .

• En ros som anges som $r=a\sin(k\theta )$ är symmetrisk kring den vertikala linjen $\theta =\pi /2$ eftersom av identiteten $a\sin(k\theta )=a\sin(\pi -k\theta )$ som gör att rosorna specificeras av de två polära ekvationerna sammanfaller.

• Endast vissa rosor är symmetriska kring stolpen.

• Enskilda kronblad är symmetriska kring linjen genom polen och kronbladets topp, vilket återspeglar symmetrin i halvcykeln av den underliggande sinusformen. Rosor som består av ett ändligt antal kronblad är, per definition, rotationssymmetriska eftersom varje kronblad har samma form med på varandra följande kronblad roterade runt samma vinkel runt polen.

Rosor med heltalsvärden k som inte är noll

Rosen $r=\cos(4\theta )$ . Eftersom $k=4$ är ​​ett jämnt tal, har rosen $2k=8$ kronblad. Linjesegment som förbinder på varandra följande toppar ligger på cirkeln $r=1$ och kommer att bilda en oktagon . Eftersom en topp är vid $(1,0)$ gör oktagonen det relativt enkelt att skissa grafen efter att halvcykelgränserna (motsvarande apotemer) har ritats.

Rosen specificerad av $r=\cos(7\theta )$ . Eftersom $k=7$ är ett udda tal, har rosen $k=7$ kronblad. Linjesegment som förbinder på varandra följande toppar ligger på cirkeln $r=1$ och kommer att bilda en heptagon . Rosen är inskriven i cirkeln $r=1$ .

När $k$ är ett heltal som inte är noll, kommer kurvan att vara rosenformad med $2k$ kronblad om $k$ är jämnt, och $k$ kronblad när $k$ är udda. Egenskaperna för dessa rosor är ett specialfall av rosor med vinkelfrekvenser $(k)$ som är rationella tal som diskuteras i nästa avsnitt av denna artikel.

• Rosen är inskriven i cirkeln $r=a$ , motsvarande den radiella koordinaten för alla dess toppar.

• Eftersom ett polärt koordinatdiagram är begränsat till polära vinklar mellan $0$ och $2\pi$ , visas det $2\pi /T=k$ cykler i Graf. Inga ytterligare punkter behöver plottas eftersom den radiella koordinaten vid $\theta =0$ är samma värde vid $\theta =2\pi$ (som är toppar för två olika positiva halv- cykler för rosor som anges av cosinusfunktionen).

• När $k$ är jämnt (och inte noll), är rosen sammansatt av $2k$ kronblad, ett för varje topp i intervallet $2\pi$ för polära vinklar som visas . Varje topp motsvarar en punkt som ligger på cirkeln $r=a$ . Linjesegment som förbinder på varandra följande toppar kommer att bilda en regelbunden polygon med ett jämnt antal hörn som har sitt centrum vid polen och en radie genom varje topp, och likaså:
  • Rosorna är symmetriska kring stolpen.
  • Rosorna är symmetriska runt varje linje genom stolpen och en topp (genom "mitten" ett kronblad) med polvinkeln mellan topparna på på varandra följande kronblad är $2\pi /2k =\pi /k$ radianer. Således har dessa rosor rotationssymmetri av storleksordningen $2k$ .
  • Rosorna är symmetriska kring varje linje som delar vinkeln mellan på varandra följande toppar, vilket motsvarar halvcykelgränser och apotem för motsvarande polygon.

• När $k$ är udda, är rosen sammansatt av $k$ kronbladen, ett för varje krön (eller dal) i intervallet $2\pi$ av polära vinklar som visas. Varje topp motsvarar en punkt som ligger på cirkeln $r=a$ . Dessa roses positiva och negativa halvcykler är sammanfallande, vilket innebär att när man graferar dem, behöver bara de positiva halvcyklerna eller endast de negativa halvcyklerna plottas för att bilda hela kurvan. (På motsvarande sätt kommer en komplett kurva att plottas genom att plotta alla kontinuerliga intervall av polära vinklar som är $\pi$ radianer långa, såsom $\theta =0$ till $\theta = \pi$ .) Linjesegment som förbinder på varandra följande toppar kommer att bilda en regelbunden polygon med ett udda antal hörn, och likaså:
  • Rosorna är symmetriska kring varje linje genom polen och en topp (genom "mitten" ett kronblad) med polaren vinkeln mellan topparna av på varandra följande kronblad är $2\pi /k$ radianer. Således har dessa rosor rotationssymmetri av ordningen $k$ .

• Rosens kronblad överlappar inte varandra.

• Rosorna kan specificeras med algebraiska kurvor av ordningen $k+1$ när k är udda, och $2(k+1)$ när k är jämnt.

Cirkeln

En ros med $k=1$ är en cirkel som ligger på polen med en diameter som ligger på polaxeln när $r=a\cos(\theta )$ . Cirkeln är kurvans enda kronblad. (Se cirkeln som bildas i slutet av nästa avsnitt.) I kartesiska koordinater är motsvarande cosinus- och sinusspecifikationer $(xa/ 2)^{2}+y^{2}=(a/2)^{2}$ och $x^{2} +(ya/2)^{2}=(a/2)^{2}$ respektive.

Quadrifolium

En ros med $k=2$ kallas en quadrifolium eftersom den har 4 kronblad. I kartesiska koordinater är cosinus- och sinusspecifikationerna $(x^{2}+y^{2})^{3}=a ^{2}(x^{2}-y^{2})^{2}$ och $(x^{2}+y ^{2})^{3}=4(axel)^{2}$ respektive.

Trifolium

En ros med $k=3$ kallas trifolium eftersom den har 3 kronblad. Kurvan kallas också för Paquerette de Mélibée. I kartesiska koordinater är cosinus- och sinusspecifikationerna $(x^{2}+y^{2})^{2}=a (x^{3}-3xy^{2})$ och $(x^{2}+y^{2} )^{2}=-a(x^{3}-3xy^{2})$ , respektive. (Se trifolium som bildas i slutet av nästa avsnitt.)

Totala och kronbladsområden

Den totala arean av en ros med formens polära ekvation

$r=a\cos(k\theta )$ eller $r=a\sin(k\theta )\,$ , där $k$ är ett heltal som inte är noll, är

${\frac {1}{2}}\int _{0}^{2\pi }(a\cos(k\theta ))^{2}\,d\theta ={ \frac {a^{2}}{2}}\left(\pi +{\frac {\sin(4k\pi )}{4k}}\right)={\frac {\pi a^{2} }{2}}$ , när $k$ är jämnt; och

${\frac {1}{ 2}}\int _{0}^{\pi }(a\cos(k\theta ))^{2}\,d\theta ={\frac {a^{2}}{2}}\vänster ({\frac {\pi }{2}}+{\frac {\sin(2k\pi )}{4k}}\right)={\frac {\pi a^{2}}{4}}$ , när $k$ är udda.

När $k$ är jämnt, finns det $2k$ kronblad; och när $k$ är udda, finns det $k$ kronblad, så arean för varje kronblad är ${\frac {\pi a^{2}}{4k }}$ .

Rosor med rationella talvärden för k

I allmänhet, när $k$ är ett rationellt tal i den irreducerbara bråkformen k $\displaystyle k=n/d}$ , där $n$ och $d$ är icke -noll heltal, antalet kronblad är nämnaren för uttrycket $1/2-1/(2k)=(nd)/ 2n$ . Detta betyder att antalet kronblad är $n$ om både $n$ och $d$ är udda, och $2n$ annars.

• I fallet när både $n$ och $d$ är udda, är de positiva och negativa halvcyklerna för sinusformen sammanfallande. Grafen för dessa rosor fylls i ett kontinuerligt intervall av polära vinklar som är $d\pi$ långt.

• När $n$ är jämnt och $d$ är udda, eller vice versa, kommer rosen att plottas helt i ett kontinuerligt polärt vinkelintervall $2d\pi$ långt. Dessutom är rosorna symmetriska kring stolpen för både cosinus- och sinusspecifikationer.
  • Dessutom, när $n$ är udda och ${\displaystyle d} är jämn,$ är rosor specificerade av cosinus- och sinuspolära ekvationer med samma värden för $a$ och $k$ överensstämmande. För ett sådant par rosor sammanfaller rosen med sinusfunktionsspecifikationen med toppen av rosen med cosinusspecifikationen på polaxeln antingen vid $\theta =d\pi /2$ eller vid $\theta =3d\pi /2$ . (Detta betyder att rosor $r=a\cos(k\theta )$ och $r=a\sin(k\theta )$ med heltalsvärden ${\displaystyle k} som inte är noll$ är aldrig sammanfallande.)

• Rosen är inskriven i cirkeln $r=a$ , motsvarande den radiella koordinaten för alla dess toppar.

Dürer-folium

En ros med $k=1/2$ kallas Dürer folium, uppkallad efter den tyske målaren och Albrecht Dürer Rosorna specificerade av $r=a\cos(\theta /2)$ och $r=a\sin(\ theta /2)$ är sammanfallande även om $a\cos(\theta /2)\neq a\sin(\theta /2)$ . I kartesiska koordinater anges rosen som $(x^{2}+y^{2}) [2(x^{2}+y^{2})-a^{2}]^{2}=a^{4}x^{2}$ .

Dürer folium är också en trisectrix , en kurva som kan användas för att trisecta vinklar.

Limaçon trisectrix

En ros med $k=1/3$ är en limaçon trisectrix som har egenskapen trisectrix kurvor som kan användas för att trisecta vinklar. Rosen har ett enda kronblad med två öglor. (Se animationen nedan.)

Exempel på rosor $r=\cos(k\theta )$ skapade med hjälp av kugghjul med olika utväxlingar. Strålarna som visas är polaxeln och $\theta =\pi /2$ . Plottning börjar vid $\theta =2\pi$ när $k$ är ett heltal, $\theta =2d\pi$ annars, och fortsätter medurs till $\theta =0$ .

Cirkeln , k =1 ( n =1, d = 1). Rosen är klar när $\theta =\pi$ nås (ett halvt varv av den lättare växeln).

Limaçon trisectrix , k =1/3 ( n =1, d =3), har ett kronblad med två öglor. Rosen är klar när $\theta =3\pi$ nås (ett och ett halvt varv av den lättare växeln).

Trifolium, k =3 ( n =3, d =1). Rosen är klar när $\theta =\pi$ nås (ett halvt varv av den lättare växeln).

Rosens 8 kronblad med k =4/5 ( n =4, d =5) är var och en, en enda slinga som skär andra kronblad. Rosen är symmetrisk kring stolpen. Rosen är komplett vid $\theta =0$ (fem varv av den lättare växeln).

Rosor med irrationella talvärden för k

En rosenkurva specificerad med ett irrationellt tal för $k$ har ett oändligt antal kronblad och kommer aldrig att slutföras. Till exempel har sinusformen $r=a\cos(\pi \theta )$ en period $T=2$ , så den har ett kronblad i det polära vinkelintervallet $-1/2\leq \theta \leq 1/2$ med en topp på polaxeln; men det finns ingen annan polär vinkel i domänen för den polära ekvationen som kommer att plotta vid koordinaterna ( $\displaystyle (a,0)}$ . Sammantaget bildar rosor som specificeras av sinusoider med vinkelfrekvenser som är irrationella konstanter en tät uppsättning (dvs de kommer godtyckligt nära att specificera varje punkt på skivan ${\displaystyle r\leq a} )$ .

Se även

• Limaçon trisectrix - har samma form som rosen med k = 1/3 .
• Quadrifolium – en rosenkurva där k = 2 .
• Maurer reste sig
• Rose (topologi)
• Sectrix av Maclaurin
• Spirograf

externa länkar

Applet för att skapa ros med k parameter

• Visual Dictionary of Special Plane Curves Xah Lee
• Interaktivt exempel med JSXGraph
• Interaktivt exempel med p5